AC Values
Each point on a sine wave has a pair of numbers associated with it. One value expresses the degree of rotation of the waveform. The degree of rotation is the angle to which the armature has turned. The second value indicates its amplitude. Zero is the maxi- mum departure of the value of an alternating current or wave from the average value. There are several methods of expressing these values.
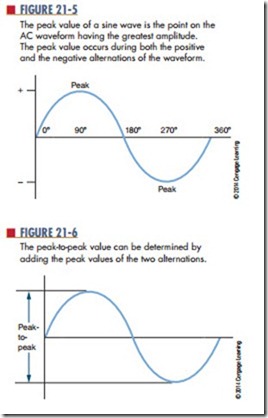
The peak value of a sine wave is the absolute value of the point on the waveform with the greatest amplitude (Figure 21-5). There are two peak values, one for the positive and one for the negative alternation. These peak values are equal.
The peak-to-peak value refers to the vertical distance between the two peaks (Figure 21-6). The peak-to-peak value can be determined by adding the absolute values of each peak.
The effective value of alternating current is the amount that produces the same degree of heat in a given resistance as an equal amount of direct current.
A mathematical process called the root-mean-square (rms) process can be used to determine the effective value . Therefore, the effective value is also referred to as the rms value. Using the rms process shows that the effective value of a sine wave is equal to 0.707 times the peak value. When an AC voltage or current is given or measured, it is assumed to be the effective value unless otherwise indicated. Most meters are cali- brated to indicate the effective, or rms, value of voltage and current.
A mathematical process called the root-mean-square (rms) process can be used to determine the effective value . Therefore, the effective value is also referred to as the rms value. Using the rms process shows that the effective value of a sine wave is equal to 0.707 times the peak value. When an AC voltage or current is given or measured, it is assumed to be the effective value unless otherwise indicated. Most meters are calibrated to indicate the effective, or rms, value of voltage and current.
The time required to complete one cycle of a sine wave is called the period (t). The period is usually measured in seconds. The letter t is used to represent the period.
The number of cycles that occurs in a specific period of time is called the frequency. The frequency of an AC sine wave is usually expressed in terms of cycles per second. The unit of frequency is the hertz. One hertz equals one cycle per second.
The period of a sine wave is inversely proportional to its frequency. The higher the frequency, the shorter the period. The relationship between the frequency and the period of a sine wave is expressed as