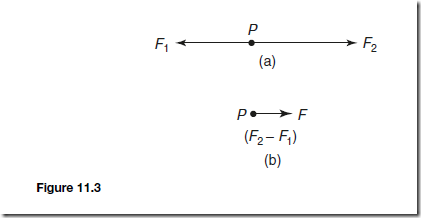Forces
When forces are all acting in the same plane, they are called coplanar. When forces act at the same time and at the same point, they are called concurrent forces.
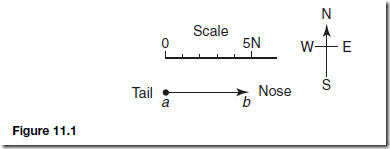
Force is a vector quantity and thus has both a magnitude and a direction. A vector can be represented graphically by a line drawn to scale in the direction of the line of action of the force.
To distinguish between vector and scalar quantities, various ways are used, as detailed in chapter 3. The method adopted in this chapter is to denote vector quantities in bold print.
Thus, ab in Figure 11.1 represents a force of 5 newtons acting in a direction due east.
The Resultant of Two Coplanar Forces
For two forces acting at a point, there are three possibilities.
(a) For forces acting in the same direction and having the same line of action, the single force having the same effect as both of the forces, called the resultant force or just the resultant, is the arithmetic sum of the separate forces. Forces of F1 and F2 acting at point P, as shown in Figure 11.2(a), have exactly the same effect on point P as force F shown in Figure 11.2(b),
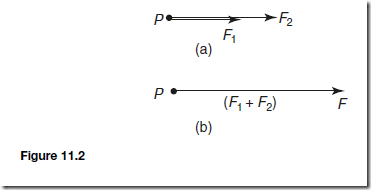
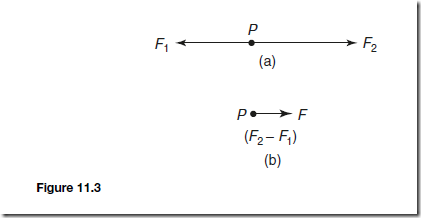
where F D F1 C F2 and acts in the same direction as F1 and F2. Thus F is the resultant of F1 and F2
(b) For forces acting in opposite directions along the same line of action, the resultant force is the arithmetic difference between the two forces. Forces of F1 and F2 acting at point P as shown in Figure 11.3(a) have exactly the same effect on point P as force F shown in Figure 11.3(b), where F D F2 Ł F1 and acts in the direction of F2, since F2 is greater than F1 .
Thus F is the resultant of F1 and F2
(c) When two forces do not have the same line of action, the magnitude and direction of the resultant force may be found by a procedure called vector addition of forces. There are two graphical methods of performing vector addition, known as the triangle of forces method and the parallelogram of forces method.
Triangle of Forces Method
A simple procedure for the triangle of forces method of vector addition is as follows:
(i) Draw a vector representing one of the forces, using an appropriate scale and in the direction of its line of action.
(ii) From the nose of this vector and using the same scale, draw a vector representing the second force in the direction of its line of action.
(iii) The resultant vector is represented in both magnitude and direction by the vector drawn from the tail of the first vector to the nose of the second vector.
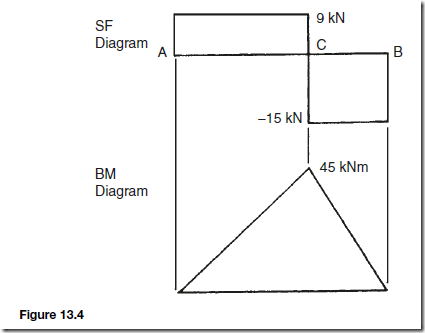
For example, to determine the magnitude and direction of the resultant of a force of 15 N acting horizontally to the right and a force of 20 N inclined at an angle of 60° to the 15 N force using the triangle of forces method:
Using the above procedure and with reference to Figure 11.4
(i) ab is drawn 15 units long horizontally
(ii) from b, bc is drawn 20 units long, inclined at an angle of 60° to ab (Note, in angular measure, an angle of 60° from ab means 60° in an anticlockwise direction)
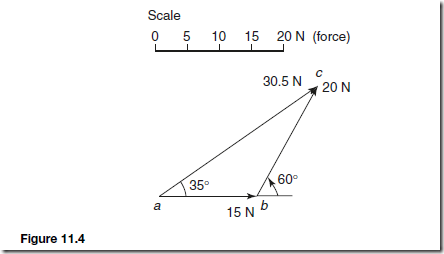
(iii) by measurement, the resultant ac is 30.5 units long inclined at an angle of 35° to ab.
Hence, the resultant force is 30.5 N, inclined at an angle of 35° to the 15 N force.
The Parallelogram of Forces Method
A simple procedure for the parallelogram of forces method of vector addition is as follows:
(i) Draw a vector representing one of the forces, using an appropriate scale and in the direction of its line of action.
(ii) From the tail of this vector and using the same scale draw a vector representing the second force in the direction of its line of action.
(iii) Complete the parallelogram using the two vectors drawn in (i) and (ii) as two sides of the parallelogram.
(iv) The resultant force is represented in both magnitude and direction by the vector corresponding to the diagonal of the parallelogram drawn from the tail of the vectors in (i) and (ii)
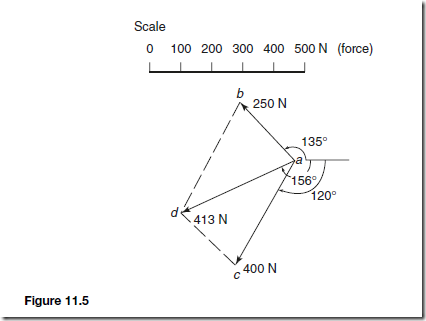
For example, to find the magnitude and direction of the resultant of a force of 250 N acting at an angle of 135° and a force of 400 N acting at an angle of Ł120° using the parallelogram of forces method:
From the above procedure and with reference to Figure 11.5:
(i) ab is drawn at an angle of 135° and 250 units in length
(ii) ac is drawn at an angle of Ł120° and 400 units in length
(iii) bd and cd are drawn to complete the parallelogram
(iv) ad is drawn. By measurement, ad is 413 units long at an angle of Ł156° .
Hence, the resultant force is 413 N at an angle of −156°
Resultant of Coplanar Forces by Calculation
An alternative to the graphical methods of determining the resultant of two coplanar forces is by calculation. This can be achieved by trigonometry using the cosine rule and the sine rule, or by resolution of forces (see later).
For example, to determine the magnitude and direction of the resultant of a force of 8 kN acting at an angle of 50° to the horizontal and a force of 5 kN acting at an angle of Ł30° to the horizontal using the cosine and sine rules:
The space diagram is shown in Figure 11.6(a). A sketch is made of the vector diagram, oa representing the 8 kN force in magnitude and direction and ab representing the 5 kN force in magnitude and direction. The resultant is given by length ob. By the cosine rule,

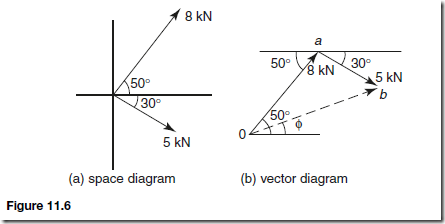
Hence the resultant of the two forces is 10.14 kN acting at an angle of 20.95° to the horizontal
Resultant of more than Two Coplanar Forces
For the three coplanar forces F1, F2 and F3 acting at a point as shown in Figure 11.7, the vector diagram is drawn using the nose-to-tail method.
The procedure is:
(i) Draw oa to scale to represent force F1 in both magnitude and direction (see Figure 11.8)
(ii) From the nose of oa, draw ab to represent force F2
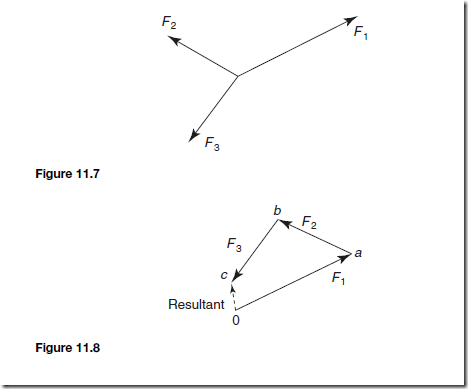
(iii) From the nose of ab, draw bc to represent force F3
(iv) The resultant vector is given by length oc in Figure 11.8. The direction
of resultant oc is from where we started, i.e. point o, to where we fin- ished, i.e. point c. When acting by itself, the resultant force, given by oc, has the same effect on the point as forces F1, F2 and F3 have when acting together. The resulting vector diagram of Figure 11.8 is called the polygon of forces.
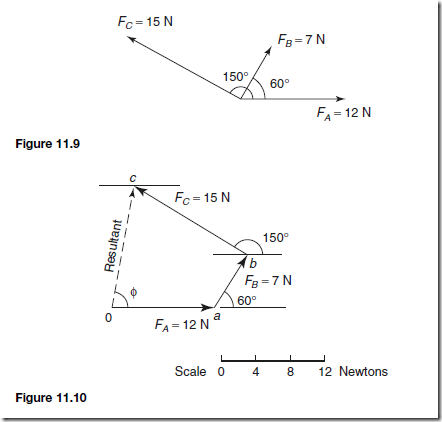
For example, three coplanar forces acting at a point are: force A, 12 N acting horizontally to the right, force B, 7 N inclined at 60° to force A, and force C, 15 N inclined at 150° to force A. The magnitude and direction of their resultant is determined graphically as follows:
The space diagram is shown in Figure 11.9. The vector diagram, shown in Figure 11.10, is produced as follows:
(i) oa represents the 12 N force in magnitude and direction
(ii) From the nose of oa, ab is drawn inclined at 60° to oa and 7 units long
(iii) From the nose of ab, bc is drawn 15 units long inclined at 150° to oa
(i.e. 150° to the horizontal)
(iv) oc represents the resultant; by measurement, the resultant is 13.8 N inclined at ¢ D 80° to the horizontal
Thus the resultant of the three forces, FA, FB and FC is a force of 13.8 N at 80° to the horizontal
Coplanar Forces in Equilibrium
When three or more coplanar forces are acting at a point and the vector diagram closes, there is no resultant. The forces acting at the point are in equilibrium.
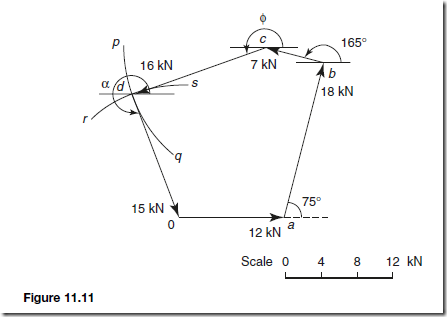
For example, five coplanar forces are acting on a body and the body is in equilibrium. The forces are: 12 kN acting horizontally to the right, 18 kN acting at an angle of 75°, 7 kN acting at an angle of 165°, 16 kN acting from the nose of the 7 kN force, and 15 kN acting from the nose of the 16 kN force. To determine the directions of the 16 kN and 15 kN forces relative to the 12 kN force:
With reference to Figure 11.11, oa is drawn 12 units long horizontally to the right. From point a, ab is drawn 18 units long at an angle of 75°. From b, bc is drawn 7 units long at an angle of 165° . The direction of the 16 kN force is not known, thus arc pq is drawn with a compass, with centre at c, radius 16 units. Since the forces are at equilibrium, the polygon of forces must close.
Using a compass with centre at 0, arc rs is drawn having a radius 15 units.
The point where the arcs intersect is at d.
By measurement, angle

Thus the 16 kN force acts at an angle of 198° (or −162° ) to the 12 kN force, and the 15 kN force acts at an angle of 291° (or −69°) to the 12 kN force.
Resolution of Forces
A vector quantity may be expressed in terms of its horizontal and vertical components.
For example, a vector representing a force of 10 N at an angle of 60° to the horizontal is shown in Figure 11.12. If the horizontal line oa and the vertical line ab are constructed as shown, then oa is called the horizontal component of the 10 N force, and ab the vertical component of the 10 N force.

This process is called finding the horizontal and vertical components of a vector or the resolution of a vector, and can be used as an alternative to graphical methods for calculating the resultant of two or more coplanar forces acting at a point.
For example, to calculate the resultant of a 10 N force acting at 60° to the horizontal and a 20 N force acting at Ł30° to the horizontal (see Figure 11.13) the procedure is as follows:
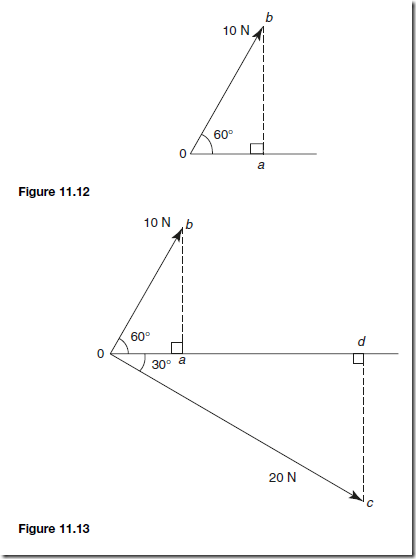

Hence the resultant of the 10 N and 20 N forces shown in Figure 11.13 is 22.36 N at an angle of −3.44° to the horizontal.
The above example demonstrates the use of resolution of forces for calculating the resultant of two coplanar forces acting at a point. However, the method may also be used for more than two forces acting at a point.
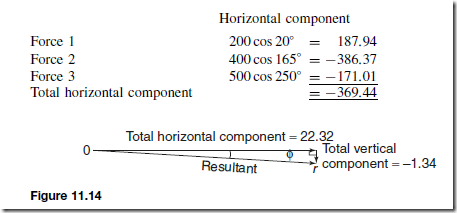
For example, three coplanar forces acting at a point are: 200 N acting at 20° to the horizontal, 400 N acting at 165° to the horizontal, and 500 N acting at 250° to the horizontal. To determine by resolution of forces the resultant of the forces:
A tabular approach using a calculator may be made as shown below.

Summary
(a) To determine the resultant of two coplanar forces acting at a point, four methods are commonly used. They are:
by drawing:
(1) triangle of forces method, and
(2) parallelogram of forces method, and
by calculation:
(3) use of cosine and sine rules, and
(4) resolution of forces
(b) To determine the resultant of more than two coplanar forces acting at a point, two methods are commonly used. They are:
by drawing:
(1) polygon of forces method, and
by calculation:
(2) resolution of forces