science universe

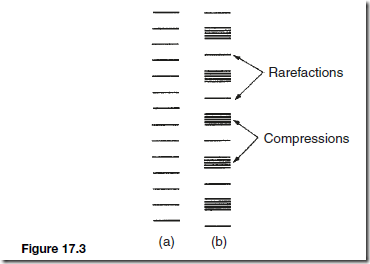
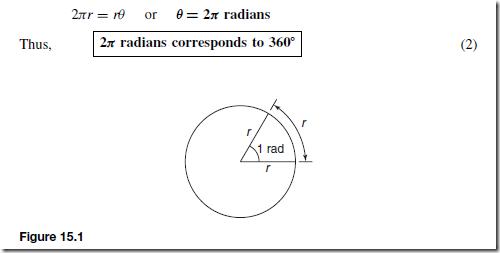
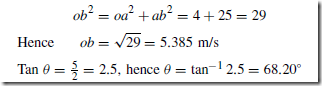Light Rays

Introduction

Light is an electromagnetic wave (see page 66) and the straight line paths followed by very narrow beams of light, along which light energy travels, are called rays.

The behaviour of light rays may be investigated by using a ray-box. This consists merely of a lamp in a box containing a narrow slit which emits rays of light.

Light always travels in straight lines although its direction can be changed by reflection or refraction.

Reflection of Light

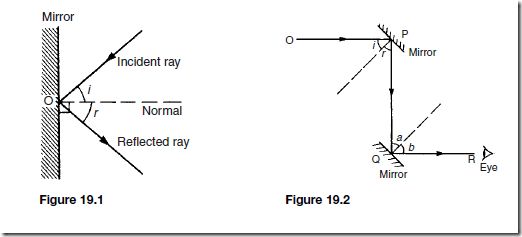
Figure 19.1 shows a ray of light, called the incident ray, striking a plane mirror at O, and making an angle i with the normal, which is a line drawn at right angles to the mirror at O.

i is called the angle of incidence. r is called the angle of reflection. There are two laws of reflection:

(i) The angle of incidence is equal to the angle of reflection (i.e. i D r in Figure 19.1)

(ii) The incident ray, the normal at the point of incidence and the reflected

ray all lie in the same plane.

A Simple Periscope

A simple periscope arrangement is shown in Figure 19.2. A ray of light from O strikes a plane mirror at an angle of 45° at point P. Since from the laws

of reflection the angle of incidence i is equal to the angle of reflection r then i = r = 45°. Thus angle OPQ = 90° and the light is reflected through 90° . The ray then strikes another mirror at 45° at point Q. Thus a = b = 45° , angle PQR = 90° and the light ray is again reflected through 90°. Thus the light from O finally travels in the direction QR, which is parallel to OP, but displaced by the distance PQ. The arrangement thus acts as a periscope.

Refraction of Light

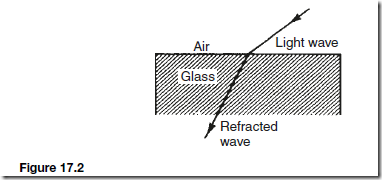
When a ray of light passes from one medium to another the light undergoes a change in direction. This displacement of light rays is called refraction.

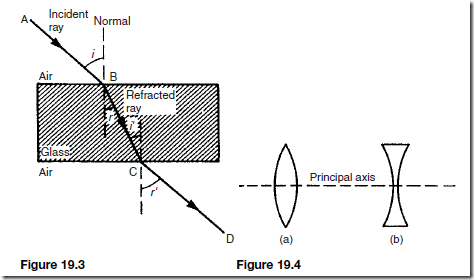
Figure 19.3 shows the path of a ray of light as it passes through a parallel- sided glass block. The incident ray AB that has an angle of incidence i enters the glass block at B. The direction of the ray changes to BC such that the angle

r is less than angle i. r is called the angle of refraction. When the ray emerges from the glass at C the direction changes to CD, angle r0 being greater than i0 . The final emerging ray CD is parallel to the incident ray AB.

Lenses

In general, when entering a more dense medium from a less dense medium, light is refracted towards the normal and when it passes from a dense to a less dense medium it is refracted away from the normal. Lenses are pieces of glass or other transparent material with a spherical surface on one or both sides. When light is passed through a lens it is refracted.

Lenses are used in spectacles, magnifying glasses and microscopes, telescopes, cameras and projectors.

There are a number of different shaped lenses and two of the most common are shown in Figure 19.4.

Figure 19.4(a) shows a bi-convex lens, so called since both its surfaces curve outwards. Figure 19.4(b) shows a bi-concave lens, so called since both

of its surfaces curve inwards. The line passing through the centre of curvature of the lens surface is called the principal axis.

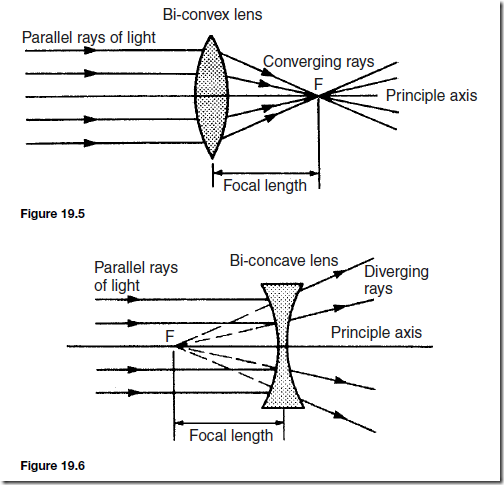
Figure 19.5 shows a number of parallel rays of light passing through a bi-convex lens. They are seen to converge at a point F on the principal axis.

Figure 19.6 shows parallel rays of light passing through a bi-concave lens.

They are seen to diverge such that they appear to come from a point F, which lies between the source of light and the lens, on the principal axis.

In both Figure 19.5 and Figure 19.6, F is called the principal focus or the focal point, and the distance from F to the centre of the lens is called the focal length of the lens.

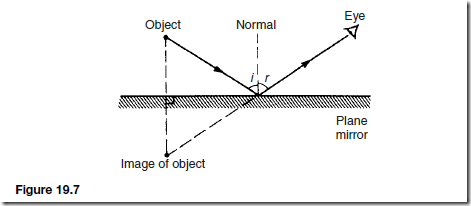
An image is the point from which reflected rays of light entering the eye appear to have originated. If the rays actually pass through the point then a real image is formed. Such images can be formed on a screen. Figure 19.7

illustrates how the eye collects rays from an object after reflection from a plane mirror. To the eye, the rays appear to come from behind the mirror and the eye sees what seems to be an image of the object as far behind the mirror as the object is in front. Such an image is called a virtual image and this type cannot be shown on a screen.

Lenses are important since they form images when an object is placed at an appropriate distance from the lens.

Bi-convex Lenses and their Applications

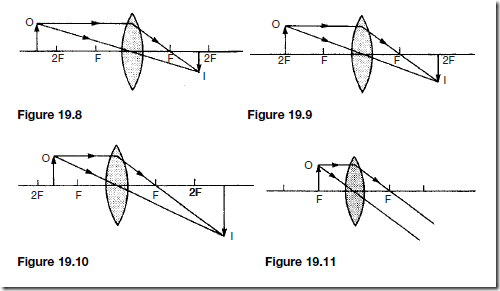
(i) Figure 19.8 shows an object O (a source of light) at a distance of more than twice the focal length from the lens. To determine the position and size of the image, two rays only are drawn, one parallel with the principal axis and the other passing through the centre of the lens. The image, I, produced is real, inverted (i.e. upside down), smaller than the object (i.e. diminished) and at a distance between one and two times the focal length from the lens. This arrangement is used in a camera.

(ii) Figure 19.9 shows an object O at a distance of twice the focal length from the lens. This arrangement is used in a photocopier.

(iii) Figure 19.10 shows an object O at a distance of between one and two focal lengths from the lens. The image I is real, inverted, magnified (i.e. greater than the object) and at a distance of more than twice the focal length from the lens. This arrangement is used in a projector

(iv) Figure 19.11 shows an object O at the focal length of the lens. After passing through the lens the rays are parallel. Thus the image I can be considered as being found at infinity and being real, inverted and very much magnified. This arrangement is used in a spotlight.

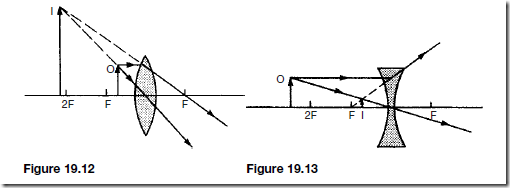
(v) Figure 19.12 shows an object O lying inside the focal length of the lens. The image I is virtual, since the rays of light only appear to come from it, is on the same side of the lens as the object, is upright and magnified. This arrangement is used in a magnifying glass.

Bi-concave Lenses

For a bi-concave lens, as shown in Figure 19.13, the object O can be any distance from the lens and the image I formed is virtual, upright, diminished and is found on the same side of the lens as the object. This arrangement is used in some types of spectacles.

A Compound Microscope

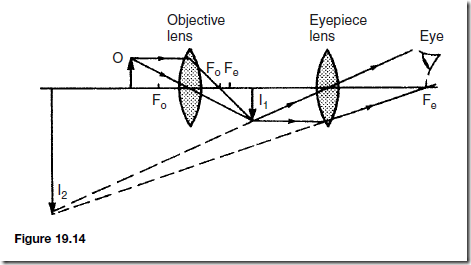
A compound microscope is able to give large magnification by the use of two (or more) lenses. An object O is placed outside the focal length Fo of a bi-convex lens, called the objective lens (since it is near to the object), as shown in Figure 19.14. This produces a real, inverted, magnified image I1.

This image then acts as the object for the eyepiece lens (i.e. the lens nearest the eye), and falls inside the focal length Fo of the lens. The eyepiece lens then produces a magnified, virtual, inverted image I2 as shown in Figure 19.14.

A Simple Projector

A simple projector arrangement is shown in Figure 19.15 and consists of a source of light and two-lens system. L is a brilliant source of light, such as a tungsten filament. One lens system, called the condenser (usually consisting of two converging lenses as shown), is used to produce an intense illumination of the object AB, which is a slide transparency or film. The second lens, called the projection lens, is used to form a magnified, real, upright image of the illuminated object on a distant screen CD.

 Interference and Diffraction

Interference

At the point where two waves cross, the total displacement is the vector sum of the individual displacements due to each wave at that point. This is the principle of superposition. If these two waves are either both transverse or both longitudinal, interference effects may be observed. It is not necessary for the two waves to have the same frequencies or amplitudes for the above statements to be true, although these are the waves considered in this chapter.

Consider two transverse waves of the same frequency and amplitude travelling in opposite directions superimposed on one another. Interference takes place between the two waves and a standing or stationary wave is produced. The standing wave is shown in Figure 18.1

The wave does not progress to the left or right and certain parts of the wave called nodes, labelled N in the diagram, do not oscillate. Those positions on the wave that undergo maximum disturbance are called antinodes, labelled

A. The distance between adjacent nodes or adjacent antinodes is , where is the wavelength. Standing waves may be set up in a string, for example, when a wave is reflected at the end of the string and is superimposed on the incoming wave. Under these circumstances standing waves are produced only for certain frequencies. Also, the nodes may not be perfect because the reflected wave may have a slightly reduced amplitude.

Two sound (longitudinal) waves of the same amplitude and frequency travelling in opposite directions and superimposed on each other also produce a standing wave. In this case there are displacement nodes where the medium does not oscillate and displacement antinodes where the displacement is a maximum.

The interference effects mentioned above are not always restricted to the line between the two sources of waves. Two dimensional interference patterns are produced on the surface of water in a ripple tank, for example. In this case, two dippers, usually oscillating in phase and with the same frequency, produce circular ripples on the surface of the water and interference takes place where the circular ripples overlap. The resulting interference pattern is shown in Figure 18.2. The sources of the waves are S1 and S2.

Diffraction

When sea waves are incident on a barrier that is parallel to them a disturbance is observed beyond the barrier in that region where it might be thought that the water would remain undisturbed. This is because waves may spread round obstacles into regions which would be in shadow if the energy travelled exactly in straight lines. This phenomenon is called diffraction. All waves whether transverse or longitudinal exhibit this property. If light, for example, is incident on a narrow slit, diffraction takes place. The diffraction pattern on the screen placed beyond the slit is not perfectly sharp. The intensity of the image varies as shown in Figure 18.3.

A consequence of diffraction is that if light from two sources that are close together pass through a slit or small circular aperture, the diffraction patterns of the two sources may overlap to such an extent that they appear to be one source. If they are to be distinguished as two separate sources, the angular separation, 8, in radians, of the two sources, must be greater than , where b is the wavelength of the light and b is the width of the slit (see Figure 18.4).

For a circular aperture the condition becomes:

If light falls on two narrow parallel slits with a small separation, light passes through both slits and because of diffraction there is an overlapping of the light and interference takes place. This is shown in Figure 18.5. The interference effects are similar to those described for water ripples above.

Suppose the light from the two slits meet at a point on a distant screen. Since the distance between the slits is much less that the slit to screen distance the two light beams will be very nearly parallel. See Figure 18.6. If the path difference is n , where n is an integer and is the wavelength there will be constructive interference and a maximum intensity occurs on the screen.

But from Figure 18.6, the path difference is BC, that is, d sin 8. Thus for a maximum intensity on the screen, n D d sin 8, that is:

The intensity of the interference pattern on the screen at various distances from the polar axis is shown in Figure 18.7. The pattern is modified by the type of diffraction pattern produced by a single slit.

A diffraction grating is similar to the two-slit arrangement, but with a very large number of slits. Very sharp values of maximum intensity are produced in this case. If the slit separation is d and light is incident along the normal to the grating, the condition for a maximum is:

If n= 2, then sin This gives the direction of the second order maximum and the path difference is 2 .

If white light is incident on a diffraction grating a continuous spectrum is produced because the angle at which the first order emerges from the grating depends on the wavelength. Thus the diffraction grating may be used to determine the wavelengths present in a source of light.

X-ray diffraction

Atoms in a crystal diffract X-rays that are incident upon them and information may be gained about crystal structure from the analysis of the diffraction pat- tern obtained. When X-rays strike atoms in a crystal, each atom scatters the X-rays in all directions. However, in certain directions constructive interference takes place. In Figure 18.8 a lattice of atoms is shown, in which X-rays strike atoms and are scattered. The X-rays emerging in a particular direction are considered.

Three planes of atoms are shown. The X-rays ‘reflected’ from the top and middle planes (and any other pair of adjacent planes) will be in phase if their path difference is n , where n is an integer and is the wavelength of the X-rays.

 Interference and Diffraction

Interference

At the point where two waves cross, the total displacement is the vector sum of the individual displacements due to each wave at that point. This is the principle of superposition. If these two waves are either both transverse or both longitudinal, interference effects may be observed. It is not necessary for the two waves to have the same frequencies or amplitudes for the above statements to be true, although these are the waves considered in this chapter.

Consider two transverse waves of the same frequency and amplitude travelling in opposite directions superimposed on one another. Interference takes place between the two waves and a standing or stationary wave is produced. The standing wave is shown in Figure 18.1

The wave does not progress to the left or right and certain parts of the wave called nodes, labelled N in the diagram, do not oscillate. Those positions on the wave that undergo maximum disturbance are called antinodes, labelled

A. The distance between adjacent nodes or adjacent antinodes is , where is the wavelength. Standing waves may be set up in a string, for example, when a wave is reflected at the end of the string and is superimposed on the incoming wave. Under these circumstances standing waves are produced only for certain frequencies. Also, the nodes may not be perfect because the reflected wave may have a slightly reduced amplitude.

Two sound (longitudinal) waves of the same amplitude and frequency travelling in opposite directions and superimposed on each other also produce a standing wave. In this case there are displacement nodes where the medium does not oscillate and displacement antinodes where the displacement is a maximum.

The interference effects mentioned above are not always restricted to the line between the two sources of waves. Two dimensional interference patterns are produced on the surface of water in a ripple tank, for example. In this case, two dippers, usually oscillating in phase and with the same frequency, produce circular ripples on the surface of the water and interference takes place where the circular ripples overlap. The resulting interference pattern is shown in Figure 18.2. The sources of the waves are S1 and S2.

Diffraction

When sea waves are incident on a barrier that is parallel to them a disturbance is observed beyond the barrier in that region where it might be thought that the water would remain undisturbed. This is because waves may spread round obstacles into regions which would be in shadow if the energy travelled exactly in straight lines. This phenomenon is called diffraction. All waves whether transverse or longitudinal exhibit this property. If light, for example, is incident on a narrow slit, diffraction takes place. The diffraction pattern on the screen placed beyond the slit is not perfectly sharp. The intensity of the image varies as shown in Figure 18.3.

A consequence of diffraction is that if light from two sources that are close together pass through a slit or small circular aperture, the diffraction patterns of the two sources may overlap to such an extent that they appear to be one source. If they are to be distinguished as two separate sources, the angular separation, 8, in radians, of the two sources, must be greater than , where b is the wavelength of the light and b is the width of the slit (see Figure 18.4).

For a circular aperture the condition becomes:

If light falls on two narrow parallel slits with a small separation, light passes through both slits and because of diffraction there is an overlapping of the light and interference takes place. This is shown in Figure 18.5. The interference effects are similar to those described for water ripples above.

Suppose the light from the two slits meet at a point on a distant screen. Since the distance between the slits is much less that the slit to screen distance the two light beams will be very nearly parallel. See Figure 18.6. If the path difference is n , where n is an integer and is the wavelength there will be constructive interference and a maximum intensity occurs on the screen.

But from Figure 18.6, the path difference is BC, that is, d sin 8. Thus for a maximum intensity on the screen, n D d sin 8, that is:

The intensity of the interference pattern on the screen at various distances from the polar axis is shown in Figure 18.7. The pattern is modified by the type of diffraction pattern produced by a single slit.

A diffraction grating is similar to the two-slit arrangement, but with a very large number of slits. Very sharp values of maximum intensity are produced in this case. If the slit separation is d and light is incident along the normal to the grating, the condition for a maximum is:

If n= 2, then sin This gives the direction of the second order maximum and the path difference is 2 .

If white light is incident on a diffraction grating a continuous spectrum is produced because the angle at which the first order emerges from the grating depends on the wavelength. Thus the diffraction grating may be used to determine the wavelengths present in a source of light.

X-ray diffraction

Atoms in a crystal diffract X-rays that are incident upon them and information may be gained about crystal structure from the analysis of the diffraction pat- tern obtained. When X-rays strike atoms in a crystal, each atom scatters the X-rays in all directions. However, in certain directions constructive interference takes place. In Figure 18.8 a lattice of atoms is shown, in which X-rays strike atoms and are scattered. The X-rays emerging in a particular direction are considered.

Three planes of atoms are shown. The X-rays ‘reflected’ from the top and middle planes (and any other pair of adjacent planes) will be in phase if their path difference is n , where n is an integer and is the wavelength of the X-rays.

Waves

Introduction to Waves

Wave motion is a travelling disturbance through a medium or through space, in which energy is transferred from one point to another without movement of matter.

Examples where wave motion occurs include:

(i) water waves, such as are produced when a stone is thrown into a still pool of water

(ii) waves on strings

(iii) waves on stretched springs

(iv) sound waves

(v) light waves (see page 75)

(vi) radio waves

(vii) infra-red waves, which are emitted by hot bodies

(viii) ultra-violet waves, which are emitted by very hot bodies and some gas discharge lamps

(ix) x-ray waves, which are emitted by metals when they are bombarded by high speed electrons

(x) gamma-rays which are emitted by radioactive elements.

Examples (i) to (iv) are mechanical waves and they require a medium (such as air or water) in order to move. Examples (v) to (x) are electromagnetic waves and do not require any medium — they can pass through a vacuum.

Wave Types

There are two types of waves, these being transverse and longitudinal waves:

(i) Transverse waves are where the particles of the medium move perpendicular to the direction of movement. For example, when a stone is thrown onto a pool of still water, the ripple moves radially outwards but the movement of a floating object shows that the water at a particular point merely moves up and down. Light and radio waves are other examples of transverse waves.

(ii) Longitudinal waves are where the particles of the medium vibrate back and forth parallel to the direction of the wave travel. Examples include sound waves and waves in springs.

Figure 17.1 shows a cross section of a typical wave.

Wavelength, Frequency and Velocity

Wavelength is the distance between two successive identical parts of a wave (for example, between two crests as shown in Figure 17.1). The symbol for wavelength is A (Greek lambda) and its unit is metres.

Frequency is the number of complete waves (or cycles) passing a fixed point in one second. The symbol for frequency is f and its unit is the hertz, Hz.

The velocity, v of a wave is given by:

The unit of velocity is metres per second.

For example , if BBC radio 4 is transmitted at a frequency of 198 kHz and a wavelength of 1500 m, the velocity of the radio wave v is given by:

Reflection and Refraction

Reflection is a change in direction of a wave while the wave remains in the same medium. There is no change in the speed of a reflected wave. All waves are reflected when they meet a surface through which they cannot pass. For example,

(i) light rays are reflected by mirrors,

(ii) water waves are reflected at the end of a bath or by a sea wall,

(iii) sound waves are reflected at a wall (which can produce an echo),

(iv) a wave reaching the end of a spring or string is reflected, and

(v) television waves are reflected by satellites above the Earth.

Experimentally, waves produced in an open tank of water may readily be observed to reflect off a sheet of glass placed at right angles to the surface of the water.

Refraction is a change in direction of a wave as it passes from one medium to another. All waves refract, and examples include:

(i) a light wave changing its direction at the boundary between air and glass, as shown in Figure 17.2,

(ii) sea waves refracting when reaching more shallow water, and

(iii) sound waves refracting when entering air of different temperature (see below).

Experimentally, if one end of a water tank is made shallow the waves may be observed to travel more slowly in these regions and are seen to change direction as the wave strikes the boundary of the shallow area. The greater the change of velocity the greater is the bending or refraction.

Sound Waves and their Characteristics

A sound wave is a series of alternate layers of air, one layer at a pressure slightly higher than atmospheric, called compressions, and the other slightly lower, called rarefactions. In other words, sound is a pressure wave. Figure 17.3(a) represents layers of undisturbed air; Figure 17.3(b) shows what happens to the air when a sound wave passes.

Sound waves exhibit the following characteristics:

(i) Sound waves can travel through solids, liquids and gases, but not through a vacuum.

(ii) Sound has a finite (i.e. fixed) velocity, the value of which depends on

the medium through which it is travelling. The velocity of sound is also affected by temperature. Some typical values for the velocity of sound are: air 331 m/s at 0°C, and 342 m/s at 18° C, water 1410 m/s at 20°C and iron 5100 m/s at 20°C.

(iii) Sound waves can be reflected, the most common example being an echo.

Echo-sounding is used for charting the depth of the sea.

(iv) Sound waves can be refracted. This occurs, for example, when sound waves meet layers of air at different temperatures. If a sound wave enters

a region of higher temperature the medium has different properties and the wave is bent as shown in Figure 17.4, which is typical of conditions

that occur at night.

Sound waves are produced as a result of vibrations.

(i) In brass instruments, such as trumpets and trombones, or wind instruments, such as clarinets and oboes, sound is due to the vibration of columns of air.

(ii) In stringed instruments, such as guitars and violins, sound is produced by vibrating strings causing air to vibrate. Similarly, the vibration of vocal chords produces speech.

(iii) Sound is produced by a tuning fork due to the vibration of the metal prongs.

(iv) Sound is produced in a loudspeaker due to vibrations in the cone.

The pitch of a sound depends on the frequency of the vibrations; the higher the frequency, the higher is the pitch. The frequency of sound depends on the form of the vibrator. The valves of a trumpet or the slide of a trombone lengthen or shorten the air column and the fingers alter the length of strings on a guitar or violin. The shorter the air column or vibrating string the higher the frequency and hence pitch. Similarly, a short tuning fork will produce a higher pitch note than a long tuning fork.

The human ear can perceive frequencies between about 20 Hz and 20 kHz.

Waves

Introduction to Waves

Wave motion is a travelling disturbance through a medium or through space, in which energy is transferred from one point to another without movement of matter.

Examples where wave motion occurs include:

(i) water waves, such as are produced when a stone is thrown into a still pool of water

(ii) waves on strings

(iii) waves on stretched springs

(iv) sound waves

(v) light waves (see page 75)

(vi) radio waves

(vii) infra-red waves, which are emitted by hot bodies

(viii) ultra-violet waves, which are emitted by very hot bodies and some gas discharge lamps

(ix) x-ray waves, which are emitted by metals when they are bombarded by high speed electrons

(x) gamma-rays which are emitted by radioactive elements.

Examples (i) to (iv) are mechanical waves and they require a medium (such as air or water) in order to move. Examples (v) to (x) are electromagnetic waves and do not require any medium — they can pass through a vacuum.

Wave Types

There are two types of waves, these being transverse and longitudinal waves:

(i) Transverse waves are where the particles of the medium move perpendicular to the direction of movement. For example, when a stone is thrown onto a pool of still water, the ripple moves radially outwards but the movement of a floating object shows that the water at a particular point merely moves up and down. Light and radio waves are other examples of transverse waves.

(ii) Longitudinal waves are where the particles of the medium vibrate back and forth parallel to the direction of the wave travel. Examples include sound waves and waves in springs.

Figure 17.1 shows a cross section of a typical wave.

Wavelength, Frequency and Velocity

Wavelength is the distance between two successive identical parts of a wave (for example, between two crests as shown in Figure 17.1). The symbol for wavelength is A (Greek lambda) and its unit is metres.

Frequency is the number of complete waves (or cycles) passing a fixed point in one second. The symbol for frequency is f and its unit is the hertz, Hz.

The velocity, v of a wave is given by:

The unit of velocity is metres per second.

For example , if BBC radio 4 is transmitted at a frequency of 198 kHz and a wavelength of 1500 m, the velocity of the radio wave v is given by:

Reflection and Refraction

Reflection is a change in direction of a wave while the wave remains in the same medium. There is no change in the speed of a reflected wave. All waves are reflected when they meet a surface through which they cannot pass. For example,

(i) light rays are reflected by mirrors,

(ii) water waves are reflected at the end of a bath or by a sea wall,

(iii) sound waves are reflected at a wall (which can produce an echo),

(iv) a wave reaching the end of a spring or string is reflected, and

(v) television waves are reflected by satellites above the Earth.

Experimentally, waves produced in an open tank of water may readily be observed to reflect off a sheet of glass placed at right angles to the surface of the water.

Refraction is a change in direction of a wave as it passes from one medium to another. All waves refract, and examples include:

(i) a light wave changing its direction at the boundary between air and glass, as shown in Figure 17.2,

(ii) sea waves refracting when reaching more shallow water, and

(iii) sound waves refracting when entering air of different temperature (see below).

Experimentally, if one end of a water tank is made shallow the waves may be observed to travel more slowly in these regions and are seen to change direction as the wave strikes the boundary of the shallow area. The greater the change of velocity the greater is the bending or refraction.

Sound Waves and their Characteristics

A sound wave is a series of alternate layers of air, one layer at a pressure slightly higher than atmospheric, called compressions, and the other slightly lower, called rarefactions. In other words, sound is a pressure wave. Figure 17.3(a) represents layers of undisturbed air; Figure 17.3(b) shows what happens to the air when a sound wave passes.

Sound waves exhibit the following characteristics:

(i) Sound waves can travel through solids, liquids and gases, but not through a vacuum.

(ii) Sound has a finite (i.e. fixed) velocity, the value of which depends on

the medium through which it is travelling. The velocity of sound is also affected by temperature. Some typical values for the velocity of sound are: air 331 m/s at 0°C, and 342 m/s at 18° C, water 1410 m/s at 20°C and iron 5100 m/s at 20°C.

(iii) Sound waves can be reflected, the most common example being an echo.

Echo-sounding is used for charting the depth of the sea.

(iv) Sound waves can be refracted. This occurs, for example, when sound waves meet layers of air at different temperatures. If a sound wave enters

a region of higher temperature the medium has different properties and the wave is bent as shown in Figure 17.4, which is typical of conditions

that occur at night.

Sound waves are produced as a result of vibrations.

(i) In brass instruments, such as trumpets and trombones, or wind instruments, such as clarinets and oboes, sound is due to the vibration of columns of air.

(ii) In stringed instruments, such as guitars and violins, sound is produced by vibrating strings causing air to vibrate. Similarly, the vibration of vocal chords produces speech.

(iii) Sound is produced by a tuning fork due to the vibration of the metal prongs.

(iv) Sound is produced in a loudspeaker due to vibrations in the cone.

The pitch of a sound depends on the frequency of the vibrations; the higher the frequency, the higher is the pitch. The frequency of sound depends on the form of the vibrator. The valves of a trumpet or the slide of a trombone lengthen or shorten the air column and the fingers alter the length of strings on a guitar or violin. The shorter the air column or vibrating string the higher the frequency and hence pitch. Similarly, a short tuning fork will produce a higher pitch note than a long tuning fork.

The human ear can perceive frequencies between about 20 Hz and 20 kHz.

Friction

Introduction to Friction

When an object, such as a block of wood, is placed on a floor and sufficient force is applied to the block, the force being parallel to the floor, the block slides across the floor. When the force is removed, motion of the block stops; thus there is a force which resists sliding. This force is called dynamic or sliding friction. A force may be applied to the block, which is insufficient to move it. In this case, the force resisting motion is called the static friction or striction. Thus there are two categories into which a frictional force may be split:

(i) dynamic or sliding friction force which occurs when motion is taking place, and

(ii) static friction force which occurs before motion takes place

There are three factors that affect the size and direction of frictional forces:

(i) The size of the frictional force depends on the type of surface (a block of wood slides more easily on a polished metal surface than on a rough concrete surface).

(ii) The size of the frictional force depends on the size of the force acting at right angles to the surfaces in contact, called the normal force; thus, if the weight of a block of wood is doubled, the frictional force is doubled when it is sliding on the same surface.

(iii) The direction of the frictional force is always opposite to the direction of motion. Thus the frictional force opposes motion, as shown in Figure 16.1.

Coefficient of Friction

The coefficient of friction, µ, is a measure of the amount of friction existing between two surfaces. A low value of coefficient of friction indicates that the force required for sliding to occur is less than the force required when the coefficient of friction is high. The value of the coefficient of friction is

The direction of the forces given in this equation is as shown in Figure 16.2 The coefficient of friction is the ratio of a force to a force, and hence has no units. Typical values for the coefficient of friction when sliding is occurring, i.e. the dynamic coefficient of friction, are:

For example, the material of a brake is being tested and it is found that the dynamic coefficient of friction between the material and steel is 0.91. The normal force, when the frictional force is 0.728 kN, is calculated as follows:

Applications of Friction

In some applications, a low coefficient of friction is desirable, for example, in bearings, pistons moving within cylinders, on ski runs, and so on. However, for such applications as force being transmitted by belt drives and braking systems, a high value of coefficient is necessary.

Advantages and Disadvantages of Frictional Forces

Instances where frictional forces are an advantage include:

(i) Almost all fastening devices rely on frictional forces to keep them in place once secured, examples being screws, nails, nuts, clips and clamps.

(ii) Satisfactory operation of brakes and clutches rely on frictional forces

being present.

(iii) In the absence of frictional forces, most accelerations along a horizontal surface are impossible; for example, a person’s shoes just slip when

walking is attempted and the tyres of a car just rotate with no forward

motion of the car being experienced.

Disadvantages of frictional forces include:

(i) Energy is wasted in the bearings associated with shafts, axles and gears due to heat being generated.

(ii) Wear is caused by friction, for example, in shoes, brake lining materials

and bearings.

(iii) Energy is wasted when motion through air occurs (it is much easier to cycle with the wind rather than against it).

Design Implications

Two examples of design implications, which arise due to frictional forces and how lubrication may or may not help, are:

(i) Bearings are made of an alloy called white metal, which has a relatively low melting point. When the rotating shaft rubs on the white metal bearing, heat is generated by friction, often in one spot and the white metal may melt in this area, rendering the bearing useless. Adequate lubrication (oil or grease) separates the shaft from the white metal, keeps the coefficient of friction small and prevents damage to the bearing. For very large bearings, oil is pumped under pressure into the bearing and the oil is used to remove the heat generated, often passing through oil coolers before being re- circulated. Designers should ensure that the heat generated by friction can be dissipated.

(ii) Wheels driving belts, to transmit force from one place to another, are used in many workshops. The coefficient of friction between the wheel and the belt must be high, and dressing the belt with a tar-like substance may increase it. Since frictional force is proportional to the normal force, a slipping belt is made more efficient by tightening it, thus increasing the normal and hence the frictional force. Designers should incorporate some belt tension mechanism into the design of such a system.

Friction

Introduction to Friction

When an object, such as a block of wood, is placed on a floor and sufficient force is applied to the block, the force being parallel to the floor, the block slides across the floor. When the force is removed, motion of the block stops; thus there is a force which resists sliding. This force is called dynamic or sliding friction. A force may be applied to the block, which is insufficient to move it. In this case, the force resisting motion is called the static friction or striction. Thus there are two categories into which a frictional force may be split:

(i) dynamic or sliding friction force which occurs when motion is taking place, and

(ii) static friction force which occurs before motion takes place

There are three factors that affect the size and direction of frictional forces:

(i) The size of the frictional force depends on the type of surface (a block of wood slides more easily on a polished metal surface than on a rough concrete surface).

(ii) The size of the frictional force depends on the size of the force acting at right angles to the surfaces in contact, called the normal force; thus, if the weight of a block of wood is doubled, the frictional force is doubled when it is sliding on the same surface.

(iii) The direction of the frictional force is always opposite to the direction of motion. Thus the frictional force opposes motion, as shown in Figure 16.1.

Coefficient of Friction

The coefficient of friction, µ, is a measure of the amount of friction existing between two surfaces. A low value of coefficient of friction indicates that the force required for sliding to occur is less than the force required when the coefficient of friction is high. The value of the coefficient of friction is

The direction of the forces given in this equation is as shown in Figure 16.2 The coefficient of friction is the ratio of a force to a force, and hence has no units. Typical values for the coefficient of friction when sliding is occurring, i.e. the dynamic coefficient of friction, are:

For example, the material of a brake is being tested and it is found that the dynamic coefficient of friction between the material and steel is 0.91. The normal force, when the frictional force is 0.728 kN, is calculated as follows:

Applications of Friction

In some applications, a low coefficient of friction is desirable, for example, in bearings, pistons moving within cylinders, on ski runs, and so on. However, for such applications as force being transmitted by belt drives and braking systems, a high value of coefficient is necessary.

Advantages and Disadvantages of Frictional Forces

Instances where frictional forces are an advantage include:

(i) Almost all fastening devices rely on frictional forces to keep them in place once secured, examples being screws, nails, nuts, clips and clamps.

(ii) Satisfactory operation of brakes and clutches rely on frictional forces

being present.

(iii) In the absence of frictional forces, most accelerations along a horizontal surface are impossible; for example, a person’s shoes just slip when

walking is attempted and the tyres of a car just rotate with no forward

motion of the car being experienced.

Disadvantages of frictional forces include:

(i) Energy is wasted in the bearings associated with shafts, axles and gears due to heat being generated.

(ii) Wear is caused by friction, for example, in shoes, brake lining materials

and bearings.

(iii) Energy is wasted when motion through air occurs (it is much easier to cycle with the wind rather than against it).

Design Implications

Two examples of design implications, which arise due to frictional forces and how lubrication may or may not help, are:

(i) Bearings are made of an alloy called white metal, which has a relatively low melting point. When the rotating shaft rubs on the white metal bearing, heat is generated by friction, often in one spot and the white metal may melt in this area, rendering the bearing useless. Adequate lubrication (oil or grease) separates the shaft from the white metal, keeps the coefficient of friction small and prevents damage to the bearing. For very large bearings, oil is pumped under pressure into the bearing and the oil is used to remove the heat generated, often passing through oil coolers before being re- circulated. Designers should ensure that the heat generated by friction can be dissipated.

(ii) Wheels driving belts, to transmit force from one place to another, are used in many workshops. The coefficient of friction between the wheel and the belt must be high, and dressing the belt with a tar-like substance may increase it. Since frictional force is proportional to the normal force, a slipping belt is made more efficient by tightening it, thus increasing the normal and hence the frictional force. Designers should incorporate some belt tension mechanism into the design of such a system.

Linear and Angular Motion

The Radian

The unit of angular displacement is the radian, where one radian is the angle subtended at the centre of a circle by an arc equal in length to the radius, as shown in Figure 15.1

The relationship between angle in radians (8), arc length (s) and radius of a circle (r) is:

Since the arc length of a complete circle is 2nr and the angle subtended at the centre is 360° , then from equation (1), for a complete circle,

Linear and Angular Velocity

Linear velocity

Linear velocity v is defined as the rate of change of linear displacement s with respect to time t, and for motion in a straight line:

The unit of linear velocity is metres per second (m/s)

Angular velocity

The speed of revolution of a wheel or a shaft is usually measured in revolutions per minute or revolutions per second but these units do not form part of a coherent system of units. The basis used in SI units is the angle turned through in one second.

Angular velocity ω is defined as the rate of change of angular displacement 8, with respect to time t, and for an object rotating about a fixed axis at a constant speed:

The unit of angular velocity is radians per second (rad/s)

An object rotating at a constant speed of n revolutions per second subtends an angle of 2nn radians in one second, that is, its angular velocity,

Equation (6) gives the relationship between linear velocity, v, and angular velocity, ω.

For example, if a wheel of diameter 540 mm is rotating at (1500/n) rev/min,

the angular velocity of the wheel and the linear velocity of a point on the rim of the wheel is calculated as follows:

From equation (5), angular velocity ω D 2nn, where n is the speed of revolution in revolutions per second, i.e.

Linear and Angular Acceleration

Linear acceleration, a, is defined as the rate of change of linear velocity with respect to time (as introduced in Chapter 8). For an object whose linear velocity is increasing uniformly:

The unit of linear acceleration is metres per second squared (m/s2). Rewriting equation (7) with v2 as the subject of the formula gives:

Angular acceleration, a, is defined as the rate of change of angular velocity with respect to time. For an object whose angular velocity is increasing uniformly:

The unit of angular acceleration is radians per second squared (rad/s2). Rewriting equation (9) with ω2 as the subject of the formula gives:

For example, if the speed of a shaft increases uniformly from 300 revolutions per minute to 800 revolutions per minute in 10s, the angular acceleration is determined as follows:

Initial angular velocity,

Further Equations of Motion

From equation (3), s D vt, and if the linear velocity is changing uniformly from v1 to v2 , then s D mean linear velocity x time

From equation (4), 8 = ωt, and if the angular velocity is changing uniformly from ω1 to ω2, then 8 D mean angular velocity ð time

Two further equations of linear motion may be derived from equations (8) and (12):

Two further equations of angular motion may be derived from equations (10) and (13):

Table 15.1 summarises the principal equations of linear and angular motion for uniform changes in velocities and constant accelerations and also gives the relationships between linear and angular quantities.

For example, the shaft of an electric motor, initially at rest, accelerates uniformly for 0.4 s at 15 rad/s2 . To determine the angle (in radians) turned through by the shaft in this time:

Relative Velocity

A vector quantity is represented by a straight line lying along the line of action of the quantity and having a length that is proportional to the size of the quantity, as shown in chapter 3. Thus ab in Figure 15.2 represents a velocity of 20 m/s, whose line of action is due west. The bold letters, ab, indicate a vector quantity and the order of the letters indicate that the time of action is from a to b.

For example, consider two aircraft A and B flying at a constant altitude, A travelling due north at 200 m/s and B travelling 30° east of north, written N 30°E, at 300 m/s, as shown in Figure 15.3.

Relative to a fixed point o, oa represents the velocity of A and ob the velocity of B.

The velocity of B relative to A, that is, the velocity at which B seems

to be travelling to an observer on A, is given by ab, and by measurement is 160 m/s in a direction E 22° N.

The velocity of A relative to B, that is, the velocity at which A seems to be travelling to an observer on B, is given by ba and by measurement is 160 m/s in a direction W 22° S.

In another example, a crane is moving in a straight line with a constant horizontal velocity of 2 m/s. At the same time it is lifting a load at a vertical velocity of 5 m/s. The velocity of the load relative to a fixed point on the earth’s surface is calculated as follows:

A vector diagram depicting the motion of the crane and load is shown in Figure 15.4. oa represents the velocity of the crane relative to a fixed point on the earth’s surface and ab represents the velocity of the load relative to the crane. The velocity of the load relative to the fixed point on the earth’s surface is ob. By Pythagoras’ theorem:

i.e. the velocity of the load relative to a fixed point on the earth’s surface is 5.385 m/s in a direction 68.20° to the motion of the crane

Linear and Angular Motion

The Radian

The unit of angular displacement is the radian, where one radian is the angle subtended at the centre of a circle by an arc equal in length to the radius, as shown in Figure 15.1

The relationship between angle in radians (8), arc length (s) and radius of a circle (r) is:

Since the arc length of a complete circle is 2nr and the angle subtended at the centre is 360° , then from equation (1), for a complete circle,

Linear and Angular Velocity

Linear velocity

Linear velocity v is defined as the rate of change of linear displacement s with respect to time t, and for motion in a straight line:

The unit of linear velocity is metres per second (m/s)

Angular velocity

The speed of revolution of a wheel or a shaft is usually measured in revolutions per minute or revolutions per second but these units do not form part of a coherent system of units. The basis used in SI units is the angle turned through in one second.

Angular velocity ω is defined as the rate of change of angular displacement 8, with respect to time t, and for an object rotating about a fixed axis at a constant speed:

The unit of angular velocity is radians per second (rad/s)

An object rotating at a constant speed of n revolutions per second subtends an angle of 2nn radians in one second, that is, its angular velocity,

Equation (6) gives the relationship between linear velocity, v, and angular velocity, ω.

For example, if a wheel of diameter 540 mm is rotating at (1500/n) rev/min,

the angular velocity of the wheel and the linear velocity of a point on the rim of the wheel is calculated as follows:

From equation (5), angular velocity ω D 2nn, where n is the speed of revolution in revolutions per second, i.e.

Linear and Angular Acceleration

Linear acceleration, a, is defined as the rate of change of linear velocity with respect to time (as introduced in Chapter 8). For an object whose linear velocity is increasing uniformly:

The unit of linear acceleration is metres per second squared (m/s2). Rewriting equation (7) with v2 as the subject of the formula gives:

Angular acceleration, a, is defined as the rate of change of angular velocity with respect to time. For an object whose angular velocity is increasing uniformly:

The unit of angular acceleration is radians per second squared (rad/s2). Rewriting equation (9) with ω2 as the subject of the formula gives:

For example, if the speed of a shaft increases uniformly from 300 revolutions per minute to 800 revolutions per minute in 10s, the angular acceleration is determined as follows:

Initial angular velocity,

Further Equations of Motion

From equation (3), s D vt, and if the linear velocity is changing uniformly from v1 to v2 , then s D mean linear velocity x time

From equation (4), 8 = ωt, and if the angular velocity is changing uniformly from ω1 to ω2, then 8 D mean angular velocity ð time

Two further equations of linear motion may be derived from equations (8) and (12):

Two further equations of angular motion may be derived from equations (10) and (13):

Table 15.1 summarises the principal equations of linear and angular motion for uniform changes in velocities and constant accelerations and also gives the relationships between linear and angular quantities.

For example, the shaft of an electric motor, initially at rest, accelerates uniformly for 0.4 s at 15 rad/s2 . To determine the angle (in radians) turned through by the shaft in this time:

Relative Velocity

A vector quantity is represented by a straight line lying along the line of action of the quantity and having a length that is proportional to the size of the quantity, as shown in chapter 3. Thus ab in Figure 15.2 represents a velocity of 20 m/s, whose line of action is due west. The bold letters, ab, indicate a vector quantity and the order of the letters indicate that the time of action is from a to b.

For example, consider two aircraft A and B flying at a constant altitude, A travelling due north at 200 m/s and B travelling 30° east of north, written N 30°E, at 300 m/s, as shown in Figure 15.3.

Relative to a fixed point o, oa represents the velocity of A and ob the velocity of B.

The velocity of B relative to A, that is, the velocity at which B seems

to be travelling to an observer on A, is given by ab, and by measurement is 160 m/s in a direction E 22° N.

The velocity of A relative to B, that is, the velocity at which A seems to be travelling to an observer on B, is given by ba and by measurement is 160 m/s in a direction W 22° S.

In another example, a crane is moving in a straight line with a constant horizontal velocity of 2 m/s. At the same time it is lifting a load at a vertical velocity of 5 m/s. The velocity of the load relative to a fixed point on the earth’s surface is calculated as follows:

A vector diagram depicting the motion of the crane and load is shown in Figure 15.4. oa represents the velocity of the crane relative to a fixed point on the earth’s surface and ab represents the velocity of the load relative to the crane. The velocity of the load relative to the fixed point on the earth’s surface is ob. By Pythagoras’ theorem:

i.e. the velocity of the load relative to a fixed point on the earth’s surface is 5.385 m/s in a direction 68.20° to the motion of the crane

Friction

Introduction to Friction

When an object, such as a block of wood, is placed on a floor and sufficient force is applied to the block, the force being parallel to the floor, the block slides across the floor. When the force is removed, motion of the block stops; thus there is a force which resists sliding. This force is called dynamic or sliding friction. A force may be applied to the block, which is insufficient to move it. In this case, the force resisting motion is called the static friction or striction. Thus there are two categories into which a frictional force may be split:

(i) dynamic or sliding friction force which occurs when motion is taking place, and

(ii) static friction force which occurs before motion takes place

There are three factors that affect the size and direction of frictional forces:

(i) The size of the frictional force depends on the type of surface (a block of wood slides more easily on a polished metal surface than on a rough concrete surface).

(ii) The size of the frictional force depends on the size of the force acting at right angles to the surfaces in contact, called the normal force; thus, if the weight of a block of wood is doubled, the frictional force is doubled when it is sliding on the same surface.

(iii) The direction of the frictional force is always opposite to the direction of motion. Thus the frictional force opposes motion, as shown in Figure 16.1.

Coefficient of Friction

The coefficient of friction, µ, is a measure of the amount of friction existing between two surfaces. A low value of coefficient of friction indicates that the force required for sliding to occur is less than the force required when the coefficient of friction is high. The value of the coefficient of friction is

The direction of the forces given in this equation is as shown in Figure 16.2 The coefficient of friction is the ratio of a force to a force, and hence has no units. Typical values for the coefficient of friction when sliding is occurring, i.e. the dynamic coefficient of friction, are:

For example, the material of a brake is being tested and it is found that the dynamic coefficient of friction between the material and steel is 0.91. The normal force, when the frictional force is 0.728 kN, is calculated as follows:

Applications of Friction

In some applications, a low coefficient of friction is desirable, for example, in bearings, pistons moving within cylinders, on ski runs, and so on. However, for such applications as force being transmitted by belt drives and braking systems, a high value of coefficient is necessary.

Advantages and Disadvantages of Frictional Forces

Instances where frictional forces are an advantage include:

(i) Almost all fastening devices rely on frictional forces to keep them in place once secured, examples being screws, nails, nuts, clips and clamps.

(ii) Satisfactory operation of brakes and clutches rely on frictional forces

being present.

(iii) In the absence of frictional forces, most accelerations along a horizontal surface are impossible; for example, a person’s shoes just slip when

walking is attempted and the tyres of a car just rotate with no forward

motion of the car being experienced.

Disadvantages of frictional forces include:

(i) Energy is wasted in the bearings associated with shafts, axles and gears due to heat being generated.

(ii) Wear is caused by friction, for example, in shoes, brake lining materials

and bearings.

(iii) Energy is wasted when motion through air occurs (it is much easier to cycle with the wind rather than against it).

Design Implications

Two examples of design implications, which arise due to frictional forces and how lubrication may or may not help, are:

(i) Bearings are made of an alloy called white metal, which has a relatively low melting point. When the rotating shaft rubs on the white metal bearing, heat is generated by friction, often in one spot and the white metal may melt in this area, rendering the bearing useless. Adequate lubrication (oil or grease) separates the shaft from the white metal, keeps the coefficient of friction small and prevents damage to the bearing. For very large bearings, oil is pumped under pressure into the bearing and the oil is used to remove the heat generated, often passing through oil coolers before being re- circulated. Designers should ensure that the heat generated by friction can be dissipated.

(ii) Wheels driving belts, to transmit force from one place to another, are used in many workshops. The coefficient of friction between the wheel and the belt must be high, and dressing the belt with a tar-like substance may increase it. Since frictional force is proportional to the normal force, a slipping belt is made more efficient by tightening it, thus increasing the normal and hence the frictional force. Designers should incorporate some belt tension mechanism into the design of such a system.