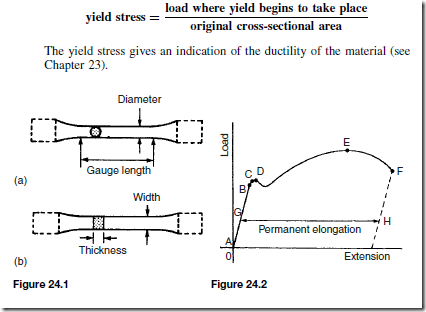
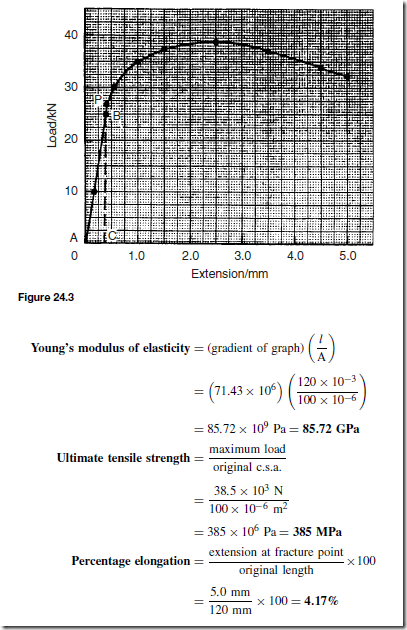
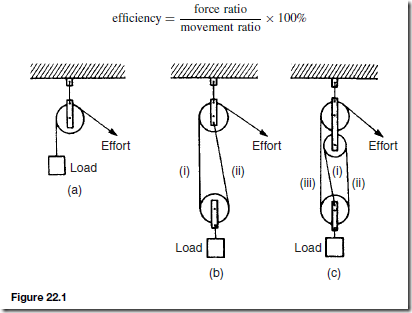
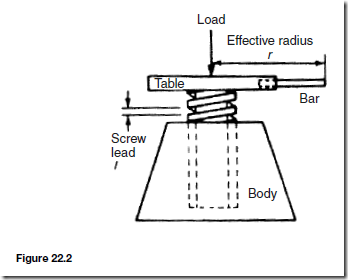
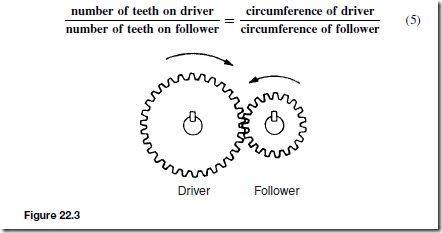
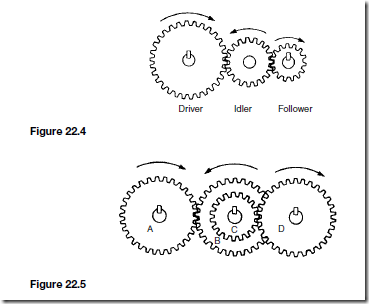
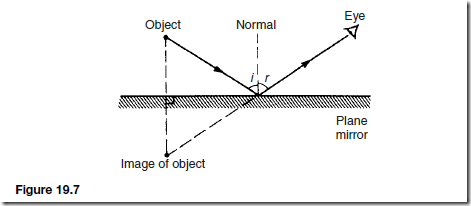
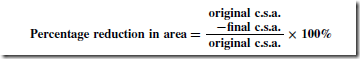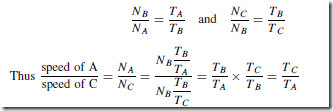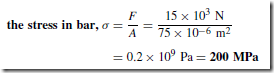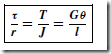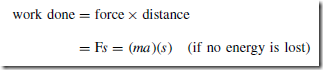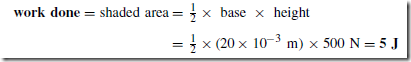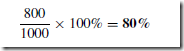The Effects of Forces on Materials
Introduction
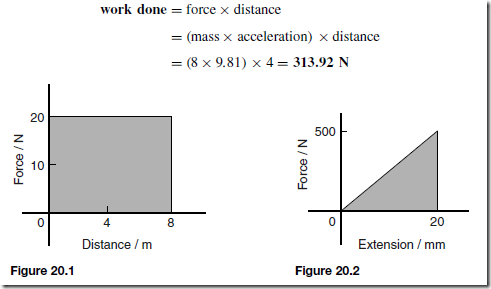
A force exerted on a body can cause a change in either the shape or the motion of the body. The unit of force is the newton, N.
No solid body is perfectly rigid and when forces are applied to it, changes in dimensions occur. Such changes are not always perceptible to the human eye since they are so small. For example, the span of a bridge will sag under the weight of a vehicle and a spanner will bend slightly when tightening a nut. It is important for engineers and designers to appreciate the effects of forces on materials, together with their mechanical properties.
The three main types of mechanical force that can act on a body are:
(i) tensile, (ii) compressive, and (iii) shear
Tensile Force
Tension is a force that tends to stretch a material, as shown in Figure 23.1. Examples include:
(i) the rope or cable of a crane carrying a load is in tension
(ii) rubber bands, when stretched, are in tension
(iii) a bolt; when a nut is tightened, a bolt is under tension
A tensile force, i.e. one producing tension, increases the length of the material on which it acts.
Compressive Force
Compression is a force that tends to squeeze or crush a material, as shown in Figure 23.2. Examples include:
(i) a pillar supporting a bridge is in compression
(ii) the sole of a shoe is in compression
(iii) the jib of a crane is in compression

A compressive force, i.e. one producing compression, will decrease the length of the material on which it acts.
Shear Force
Shear is a force that tends to slide one face of the material over an adjacent face. Examples include:
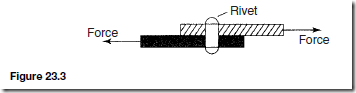
(i) a rivet holding two plates together is in shear if a tensile force is applied between the plates — as shown in Figure 23.3
(ii) a guillotine cutting sheet metal, or garden shears, each provide a shear
force
(iii) a horizontal beam is subject to shear force
(iv) transmission joints on cars are subject to shear forces
A shear force can cause a material to bend, slide or twist.
Stress
Forces acting on a material cause a change in dimensions and the material is said to be in a state of stress. Stress is the ratio of the applied force F to cross-sectional area A of the material. The symbol used for tensile and compressive stress is a (Greek letter sigma). The unit of stress is the Pascal,
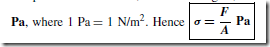
where F is the force in newtons and A is the cross-sectional area in square metres.
For tensile and compressive forces, the cross-sectional area is that which is at right angles to the direction of the force.
For example, a rectangular bar having a cross-sectional area of 75 mm2 has a tensile force of 15 kN applied to it. Then
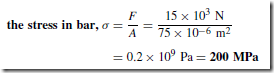
Strain
The fractional change in a dimension of a material produced by a force is called the strain. For a tensile or compressive force, strain is the ratio of the change of length to the original length. The symbol used for strain is ε (Greek epsilon). For a material of length l metres which changes in length by an amount x metres when subjected to stress,

Shear Stress and Strain
For a shear force, the shear strain is equal to force area , where the area is that which is parallel to the direction of the force. The symbol for shear stress is the Greek letter tau, r
force area , where the area is that which is parallel to the direction of the force. The symbol for shear stress is the Greek letter tau, r

For any metal the modulus of rigidity G is approximately 0.4 of the modulus of elasticity E.
Torsional Stress and Strain
With reference to Figure 23.5: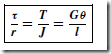
For example, a hollow shaft of length 2.4 m, has external and internal diameters of 100 mm and 80 mm. The torque the shaft can transmit if the maximum permissible shear stress is 45 MPa is given by:

Elasticity and Elastic Limit
Elasticity is the ability of a material to return to its original shape and size on the removal of external forces.
Plasticity is the property of a material of being permanently deformed by a force without breaking. Thus if a material does not return to the original shape, it is said to be plastic.
Within certain load limits, mild steel, copper, polythene and rubber are examples of elastic materials; lead and plasticine are examples of plastic materials.
If a tensile force applied to a uniform bar of mild steel is gradually increased and the corresponding extension of the bar is measured, then pro- vided the applied force is not too large, a graph depicting these results is likely to be as shown in Figure 23.6. Since the graph is a straight line, extension is directly proportional to the applied force.
If the applied force is large, it is found that the material no longer returns to its original length when the force is removed. The material is then said to have passed its elastic limit and the resulting graph of force/extension is no longer a straight line. Stress, a D A , from above, and since, for a particular bar, area A can be considered as a constant, then F a. x  Strain ε D l , from above, and since for a particular bar l is constant, then x / ε. Hence for stress applied to a material below the elastic limit a graph of stress/strain will be as shown in Figure 23.7, and is a similar shape to the force/extension graph of Figure 23.6
Strain ε D l , from above, and since for a particular bar l is constant, then x / ε. Hence for stress applied to a material below the elastic limit a graph of stress/strain will be as shown in Figure 23.7, and is a similar shape to the force/extension graph of Figure 23.6
Hooke’s Law
Hooke’s law states:
Within the elastic limit, the extension of a material is proportional to the applied force
It follows, from above, that:
Within the elastic limit of a material, the strain produced is directly proportional to the stress producing it
Young’s modulus of elasticity
Within the elastic limit, stress ˛ strain, hence
stress = (a constant) x strain
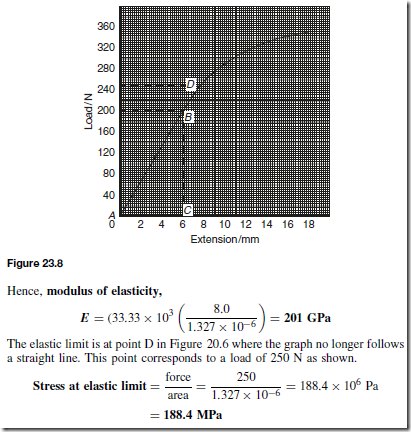
This constant of proportionality is called Young’s modulus of elasticity and is given the symbol E. The value of E may be determined from the gradient of the straight line portion of the stress/strain graph. The dimensions of E are pascals (the same as for stress, since strain is dimension-less).

Some typical values for Young’s modulus of elasticity, E, include: Aluminium 70 GPa (i.e. 70 ð 109 Pa), brass 90 GPa, copper 96 GPa, diamond 1200 GPa, mild steel 210 GPa, lead 18 GPa, tungsten 410 GPa, cast iron 110 GPa, zinc 85 GPa
Stiffness
A material having a large value of Young’s modulus is said to have a high value of stiffness, where stiffness is defined as:

Ductility, Brittleness and Malleability
Ductility is the ability of a material to be plastically deformed by elongation, without fracture. This is a property that enables a material to be drawn out into wires. For ductile materials such as mild steel, copper and gold, large extensions can result before fracture occurs with increasing tensile force. Ductile materials usually have a percentage elongation value of about 15% or more.
Brittleness is the property of a material manifested by fracture without appreciable prior plastic deformation. Brittleness is a lack of ductility, and brittle materials such as cast iron, glass, concrete, brick and ceramics, have virtually no plastic stage, the elastic stage being followed by immediate fracture. Little or no ‘waist’ occurs before fracture in a brittle material undergoing a tensile test.
Malleability is the property of a material whereby it can be shaped when cold by hammering or rolling. A malleable material is capable of undergoing plastic deformation without fracture. Examples of malleable materials include lead, gold, putty and mild steel.