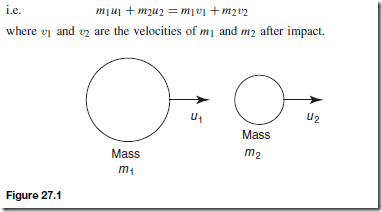
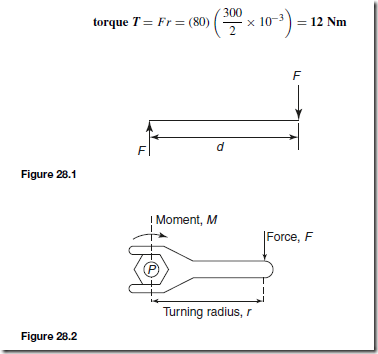
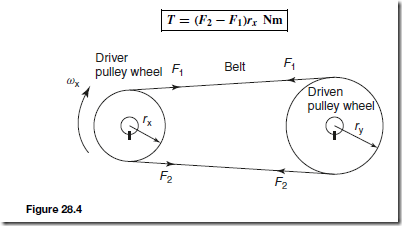
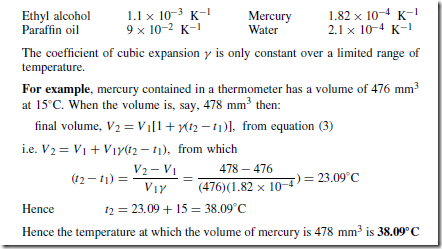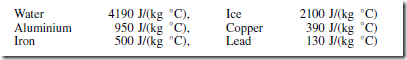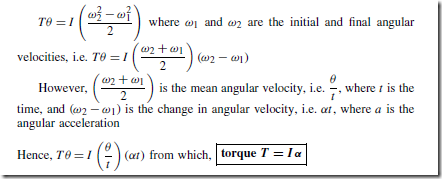Heat Energy
Introduction
Heat is a form of energy and is measured in joules.
Temperature is the degree of hotness or coldness of a substance. Heat and temperature are thus not the same thing. For example, twice the heat energy is needed to boil a full container of water than half a container — that is, different amounts of heat energy are needed to cause an equal rise in the temperature of different amounts of the same substance.
Temperature is measured either (i) on the Celsius (°C) scale (formerly Centigrade), where the temperature at which ice melts, i.e. the freezing point of water, is taken as 0°C and the point at which water boils under normal atmospheric pressure is taken as 100° C, or (ii) on the thermodynamic scale, in which the unit of temperature is the kelvin (K). The kelvin scale uses the same temperature interval as the Celsius scale but as its zero takes the ‘absolute zero of temperature’ which is at about Ð273° C. Hence,

The Measurement of Temperature
A thermometer is an instrument that measures temperature. Any substance that possesses one or more properties that vary with temperature can be used to measure temperature. These properties include changes in length, area or volume, electrical resistance or in colour. Examples of temperature measuring devices include:
(i) liquid-in-glass thermometer, which uses the expansion of a liquid with increase in temperature as its principle of operation
(ii) thermocouples, which use the e.m.f. set up when the junction of two
dissimilar metals is heated
(iii) resistance thermometer, which uses the change in electrical resistance caused by temperature change, and
(iv) pyrometers, which are devices for measuring very high temperatures, using the principle that all substances emit radiant energy when hot, the rate of emission depending on their temperature.
Each of these temperature measuring devices, together with others, are described in Chapter 31.
Specific Heat Capacity
The specific heat capacity of a substance is the quantity of heat energy required to raise the temperature of 1 kg of the substance by 1°C.
The symbol used for specific heat capacity is c and the units are J/(kg °C) or J/(kg K). (Note that these units may also be written as J kgÐ1 °CÐ1 or J kgÐ1 KÐ1)
Some typical values of specific heat capacity for the range of temperature 0°C to 100° C include:
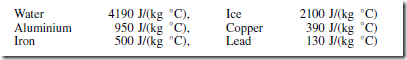
Hence, to raise the temperature of 1 kg of iron by 1°C requires 500 J of energy, to raise the temperature of 5 kg of iron by 1°C requires (500 ð 5) J of energy, and to raise the temperature of 5 kg of iron by 40°C requires (500 ð 5 ð 40) J of energy, i.e. 100 kJ
In general, the quantity of heat energy, Q, required to raise a mass m kg of a substance with a specific heat capacity c J/(kg °C) from temperature t1°C

Change of State
A material may exist in any one of three states — solid, liquid or gas. If heat is supplied at a constant rate to some ice initially at, say, Ð30°C, its temperature rises as shown in Figure 29.1. Initially the temperature increases from Ð30°C to 0°C as shown by the line AB. It then remains constant at 0°C for the time BC required for the ice to melt into water.
When melting commences the energy gained by continual heating is offset by the energy required for the change of state and the temperature remains constant even though heating is continued. When the ice is completely melted to water, continual heating raises the temperature to 100°C, as shown by CD in Figure 29.1. The water then begins to boil and the temperature again remains constant at 100°C, shown as DE, until all the water has vaporised.
Continual heating raises the temperature of the steam as shown by EF in the region where the steam is termed superheated.
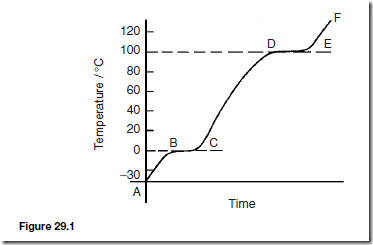
Changes of state from solid to liquid or liquid to gas occur without change of temperature and such changes are reversible processes. When heat energy flows to or from a substance and causes a change of temperature, such as between A and B, between C and D and between E and F in Figure 29.1, it is called sensible heat (since it can be ‘sensed’ by a thermometer).
Heat energy which flows to or from a substance while the temperature remains constant, such as between B and C and between D and E in Figure 29.1, is called latent heat (latent means concealed or hidden).
Latent Heats of Fusion and Vaporisation
The specific latent heat of fusion is the heat required to change 1 kg of a substance from the solid state to the liquid state (or vice versa) at constant temperature.
The specific latent heat of vaporisation is the heat required to change 1 kg of a substance from a liquid to a gaseous state (or vice versa) at constant temperature.
The units of the specific latent heats of fusion and vaporisation are J/kg, or more often kJ/kg, and some typical values are shown in Table 29.1
The quantity of heat Q supplied or given out during a change of state is given by:
Q = mL
where m is the mass in kilograms and L is the specific latent heat.
For example, the heat required to convert 10 kg of ice at 0°C to water at 0°C is given by 10 kg ð 335 kJ/kg D 3350 kJ or 3.35 MJ.
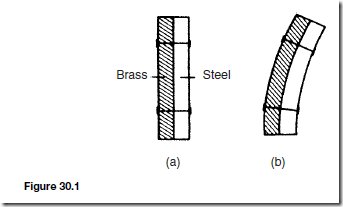
Besides changing temperature, the effects of supplying heat to a material can involve changes in dimensions, as well as in colour, state and electrical resistance. Most substances expand when heated and contract when cooled, and there are many practical applications and design implications of thermal movement (see Chapter 30).
Principle of Operation of a Simple Refrigerator
The boiling point of most liquids may be lowered if the pressure is lowered. In a simple refrigerator a working fluid, such as ammonia or freon, has the pressure acting on it reduced. The resulting lowering of the boiling point causes the liquid to vaporise. In vaporising, the liquid takes in the necessary latent heat from its surroundings, i.e. the freezer, which thus becomes cooled. The vapour is immediately removed by a pump to a condenser that is outside of the cabinet, where it is compressed and changed back into a liquid, giving out latent heat. The cycle is repeated when the liquid is pumped back to the freezer to be vaporised.
Conduction, Convection and Radiation
Heat may be transferred from a hot body to a cooler body by one or more of three methods, these being: (a) by conduction, (b) by convection, or (c) by radiation.
Conduction
Conduction is the transfer of heat energy from one part of a body to another (or from one body to another) without the particles of the body moving.
Conduction is associated with solids. For example, if one end of a metal bar is heated, the other end will become hot by conduction. Metals and metallic alloys are good conductors of heat, whereas air, wood, plastic, cork, glass and gases are examples of poor conductors (i.e. they are heat insulators).
Practical applications of conduction include:
(i) A domestic saucepan or dish conducts heat from the source to the contents.
Also, since wood and plastic are poor conductors of heat they are used for saucepan handles.
(ii) The metal of a radiator of a central heating system conducts heat from the hot water inside to the air outside.
Convection
Convection is the transfer of heat energy through a substance by the actual movement of the substance itself. Convection occurs in liquids and gases, but not in solids. When heated, a liquid or gas becomes less dense. It then rises and is replaced by a colder liquid or gas and the process repeats. For example, electric kettles and central heating radiators always heat up at the top first.
Examples of convection are:
(i) Natural circulation hot water heating systems depend on the hot water rising by convection to the top of the house and then falling back to the bottom of the house as it cools, releasing the heat energy to warm the house as it does so.
(ii) Convection currents cause air to move and therefore affect climate.
(iii) When a radiator heats the air around it, the hot air rises by convection and cold air moves in to take its place.
(iv) A cooling system in a car radiator relies on convection.
(v) Large electrical transformers dissipate waste heat to an oil tank. The heated oil rises by convection to the top, then sinks through cooling fins, losing heat as it does so.
(vi) In a refrigerator, the cooling unit is situated near the top. The air sur-
rounding the cold pipes become heavier as it contracts and sinks towards the bottom. Warmer, less dense air is pushed upwards and in turn is cooled. A cold convection current is thus created.
Radiation
Radiation is the transfer of heat energy from a hot body to a cooler one by electromagnetic waves. Heat radiation is similar in character to light waves (see Chapter 19) — it travels at the same speed and can pass through a vacuum — except that the frequency of the waves are different. Waves are emitted by a hot body, are transmitted through space (even a vacuum) and are not detected until they fall on to another body. Radiation is reflected from shining, polished surfaces but absorbed by dull, black surfaces.
Practical applications of radiation include:
(i) heat from the sun reaching earth
(ii) heat felt by a flame
(iii) cooker grills
(iv) industrial furnaces
(v) infra-red space heaters
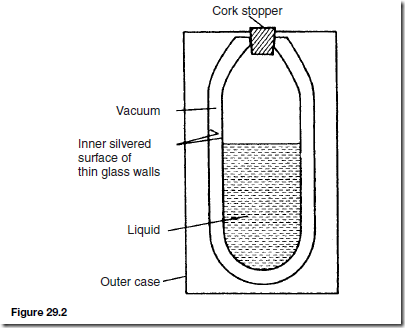
Vacuum Flask
A cross-section of a typical vacuum flask is shown in Figure 29.2 and is seen to be a double-walled bottle with a vacuum space between them, the whole supported in a protective outer case.
Very little heat can be transferred by conduction because of the vacuum space and the cork stopper (cork is a bad conductor of heat). Also, because of the vacuum space, no convection is possible. Radiation is minimised by silvering the two glass surfaces (radiation is reflected off shining surfaces).
Thus a vacuum flask is an example of prevention of all three types of heat transfer and is therefore able to keep hot liquids hot and cold liquids cold.
Use of Insulation in Conserving Fuel
Fuel used for heating a building is becoming increasingly expensive. By the careful use of insulation, heat can be retained in a building for longer periods and the cost of heating thus minimised.
(i) Since convection causes hot air to rise it is important to insulate the roof space, which is probably the greatest source of heat loss in the home. This can be achieved by laying fibre-glass between the wooden joists in the roof space.
(ii) Glass is a poor conductor of heat. However, large losses can occur through thin panes of glass and such losses can be reduced by using double-glazing. Two sheets of glass, separated by air, are used. Air is a very good insulator but the air space must not be too large otherwise convection currents can occur which would carry heat across the space.
(iii) Hot water tanks should be lagged to prevent conduction and convection of heat to the surrounding air.
(iv) Brick, concrete, plaster and wood are all poor conductors of heat. A house is made from two walls with an air gap between them. Air is a poor conductor and trapped air minimises losses through the wall. Heat losses through the walls can be prevented almost completely by using cavity wall insulation, i.e. plastic-foam.
Besides changing temperature, the effects of supplying heat to a material can involve changes in dimensions, as well as in colour, state and electrical resistance.
Most substances expand when heated and contract when cooled, and there are many practical applications and design implications of thermal movement as explained in Chapter 30 following.