7–8 RESISTORS
Resistors are one of the most common components found in electric circuits. The unit of measure for resistance is the ohm, which was named for the German scientist Georg S. Ohm. The symbol used to represent resistance is the uppercase Greek letter omega (V).
Resistors come in various sizes, types, and ratings to accommodate the needs of almost any circuit application. Resistors are commonly used to perform two functions in a circuit. One is to limit the flow of current through the circuit.
In Figure 7–17 a 30-ohm resistor is connected to a 15-volt battery. The current in this circuit is limited to a value of 0.5 ampere:
If this resistor were not present, the circuit current would be limited only by the resistance of the conductor, which would be very low and would allow a large amount of current to flow. Assume for example that the wire has a resistance of 0.0001 ohm. When the wire is connected across the 15-volt power source, a current of 150,000 amperes would try to flow through the circuit (15/0.0001 5 150,000). This is commonly known as a short circuit.
The second principal function of resistors is to produce a voltage divider, as shown in Figure 7–18. These three resistors are connected in series with a 17.5-volt battery. A volt- meter placed between different points in the circuit would indicate the following voltages:
By connecting resistors of the proper value, almost any voltage desired can be obtained. Voltage dividers were used to a large extent in vacuum tube circuits many years ago. Voltage divider circuits are still used today in applications involving field effect transistors (FETs) and in multirange voltmeter circuits.
7–9 FIXED RESISTORS
Fixed resistors have only one ohmic value that cannot be changed or adjusted. There are several different types of fixed resistors.
Carbon Resistors
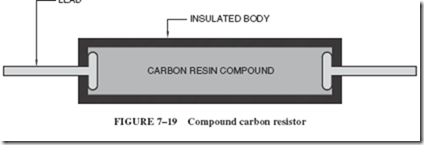
One of the most common types of fixed resistors is the composition carbon resistor. These resistors are made from a compound of carbon graphite and a resin bonding material enclosed in a case of nonconductive material with connecting leads, as shown in Figure 7–19. The proportions of carbon and resin material determine the value of resistance.
Carbon resistors are very popular for most applications because they are inexpensive and readily available. They are made in standard values that range from about 1 ohm to
about 22 million ohms and can be obtained in power ratings of 1/8, 1/4, 1/2, 1, and 2 watts. The power rating of the resistor is indicated by its size. A 1/2-watt resistor is approximately 3/8 inch long and 1/8 inch in diameter. A 2-watt resistor is approximately 11/16 inch long and approximately 5/16 inch in diameter, Figure 7–20. The 2-watt resistor is larger than the 1/2-watt or 1-watt resistor because it must have a larger surface area to be able to dissipate more heat. Although carbon resistors have many desirable characteristics, they have one characteristic that is not so desirable: Carbon resistors will change their value with age or if they are overheated. Carbon resistors generally increase instead of decrease in value.
Metal Film Resistors
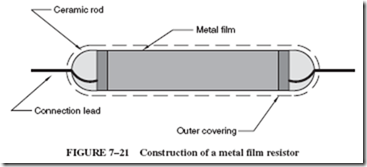
Another type of fixed resistor is the metal film resistor, constructed by applying a film of metal to a ceramic rod in a vacuum; see Figure 7–21. The resistance is determined by the type of metal used to form the film and the thickness of the film. Typical thickness for the film is from 0.000 01 to 0.000 000 01 inch. Leads are then attached to the film coating and the entire assembly is covered with a coating. Metal film resistors are superior to carbon resistors in several respects. They do not change their value with age, and their tolerance is generally better than carbon resistors. Also, carbon resistors commonly have a tolerance range of 20%, 10%, or 5% compared to the metal film resistor’s general range of 2% to 0.1%. The disadvantage of the metal film resistor is that it is higher in cost.
Carbon Film Resistors
Constructed in a similar manner as the metal film resistor, the carbon film resistor is made by coating a ceramic rod with a film of carbon instead of metal. Carbon film resistors are less expensive to manufacture than metal film resistors and can have a higher tolerance rating than composition carbon resistors.
Metal Glaze Resistors
Another resistor that is similar to the metal film one is the metal glaze resistor. This resistor is made by combining metal with glass. The compound is then applied to a ceramic base as a thick film. The resistance is determined by the amount of metal used in the compound. Tolerance ratings of 2% and 1% are common.
Wire Wound Resistors
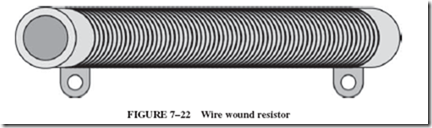
Wire wound resistors are made by winding a piece of resistive wire around a ceramic core; see Figure 7–22. The resistance of a wire wound resistor is determined by the type of material used to make the resistive wire, the diameter of the wire, and the length of the wire.
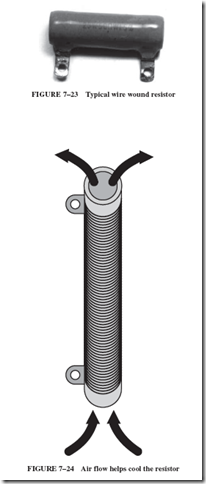
Wire wound resistors can be found in various case styles and sizes. These resistors are generally used when a high power rating is needed. Wire wound resistors can operate at higher temperatures than any other type of resistor. A wire wound resistor with a hollow center is shown in Figure 7–23. The center of the resistor is hollow for a very good reason: When the resistor is mounted vertically (as it must be), the heat from the resistor produces a chimney effect and causes air to circulate through the center; see Figure 7–24.
7–10 COLOR CODE
The values of a resistor can often be determined by the color code. Many resistors have bands of color that are used to determine the resistance value, tolerance, and, in some cases, reliability. Each color in the band represents a different numerical value, as shown in Figure 7–25. The resistor shown beside the color chart illustrates how to determine the value of a resistor. Resistors can have from three to five bands of color. Resistors with a tolerance of 620% have only three color bands, but most resistors have four. For resistors with tolerances that range from 610% to 62%, the first two color bands represent numerical values. The third band is called the multiplier, which indicates how many times the first two numbers should be multiplied by 10 to obtain the resistance value. The fourth band indicates the tolerance.
For example, assume a resistor has color bands of brown, green, red, and silver, as shown in Figure 7–26. The first two colors represent the numbers 1 and 5 (brown is 1 and green is 5). The third band is red, which represents 2. Thus the number 15 should be multiplied by 10 two times, and the value of the resistor is 1,500 ohms. Another method, which is simpler to understand, is to add to the first two numbers the number of zeros indicated by the multiplier band. With the red multiplier band in our example representing a numeric value of 2, we add two zeros to the first two numbers and the number 15 becomes 1,500.
The brown fifth band indicates that this resistor has a tolerance of 61%. To determine the value of a 1% resistor, note that the first three bands are numbers and the fourth band is the multiplier. In this example, the first band is brown, which has a numerical value of 1. The next two bands are black, which represents 0. The fourth band is brown, which means add one 0 to the first three numbers. The value of this resistor is 1,000 ohms 61%.
EXAMPLE 7–9
A five-band resistor has the following color bands:
The first three bands represent numerical values: Red is 2, orange is 3, and violet is 7. The red fourth band is the multiplier; in this case red represents 2. Add two 0’s to the number 237 to find that the value of the resistor is 23,700 ohms. The brown fifth band indicates a tolerance of 61%.
Military resistors often have five color bands also. These resistors are read resistors with four color bands. The fifth band can represent different things. A fifth band of orange or yellow is used to indicate reliability. Resistors with a fifth band of orange have a reliability good enough to be used in missile systems, and those with a fifth band of yellow can be used in space flight equipment. A fifth band of white indicates that the resistor has solderable leads. Resistors with tolerance ratings ranging from 0.5% to 0.1% will generally have their values printed directly on the resistor.
Gold and Silver as Multipliers
The colors gold and silver are generally found in the fourth band of a resistor, but they can be used in the multiplier band also. A gold multiplier band means to divide the first two numbers by 10. A silver multiplier band means to divide the first two numbers by 100. For example, assume a resistor has color bands of orange, white, gold, and gold. Orange 5 3, white 5 9, gold means to divide 39 by 10 (which equals 3.9), and gold in the fourth band means 65% tolerance. The value of this resistor is 3.9 ohms with a tolerance of 65%.
Standard Resistance Values
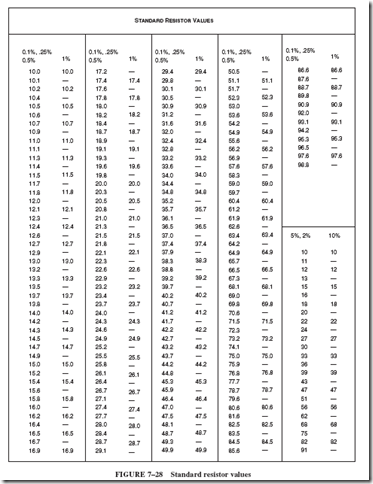
Fixed resistors are generally produced in standard values. The higher the tolerance value, the fewer resistance values available. Standard resistor values are listed in Figure 7–28. In the column under 10%, there are only 12 values of resistors listed. These values, however, can be multiplied by factors of 10. For example, one of the standard values listed is 33 ohms. There are also standard values in 10% resistors of 0.33; 3.3; 330; 3,300; 33,000; 330,000; and 3,300,000 ohms. The 5% column shows there are 24 resistor values and the 1% column lists 96 values. All the values listed in the chart can be multi- plied by factors of 10 to obtain other resistance values.



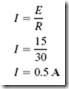













![image_thumb[9] image_thumb[9]](http://lh4.ggpht.com/-_XERF88upPU/VKmHlb25QrI/AAAAAAABATo/jR2CL2NkKfc/image_thumb%25255B9%25255D_thumb.png?imgmax=800)
![image_thumb[10] image_thumb[10]](http://lh5.ggpht.com/-UunJluJnXdo/VKmHqZbqZYI/AAAAAAABAUI/CeWF3IzOCFU/image_thumb%25255B10%25255D_thumb.png?imgmax=800)
![image_thumb[11] image_thumb[11]](http://lh4.ggpht.com/-BtWHa0zZ2qA/VKmHufu5wpI/AAAAAAABAUo/Iw-3BpPilcw/image_thumb%25255B11%25255D_thumb.png?imgmax=800)
![image_thumb[12] image_thumb[12]](http://lh5.ggpht.com/-SVG4L8hVgNY/VKmHywoANDI/AAAAAAABAVA/coiGGZwjwco/image_thumb%25255B12%25255D_thumb.png?imgmax=800)
![image_thumb[13] image_thumb[13]](http://lh5.ggpht.com/-MA3SKsCPwq0/VKmH33owCrI/AAAAAAABAVQ/Yc1TTEBtwaM/image_thumb%25255B13%25255D_thumb.png?imgmax=800)
![image_thumb[14] image_thumb[14]](http://lh5.ggpht.com/-G79WojqkkEA/VKmH9iopsOI/AAAAAAABAVg/0m375kutBuo/image_thumb%25255B14%25255D_thumb.png?imgmax=800)
![image_thumb[15] image_thumb[15]](http://lh6.ggpht.com/-tBC2QoQ75c0/VKmIBmk6mCI/AAAAAAABAVw/LfTEJaPnm1w/image_thumb%25255B15%25255D_thumb.png?imgmax=800)
![image_thumb[16] image_thumb[16]](http://lh4.ggpht.com/-47qwkMKsRJs/VKmIETCZQDI/AAAAAAABAWA/mfFzbzasiSo/image_thumb%25255B16%25255D_thumb.png?imgmax=800)
![image_thumb[17] image_thumb[17]](http://lh3.ggpht.com/-uBLFQP_sMTk/VKmIHOZFMjI/AAAAAAABAWQ/eO73id0eT4Y/image_thumb%25255B17%25255D_thumb.png?imgmax=800)
![image_thumb[18] image_thumb[18]](http://lh6.ggpht.com/-ZNDXconzJS0/VKmIJxdZuvI/AAAAAAABAWg/UfvxfzXU3hQ/image_thumb%25255B18%25255D_thumb.png?imgmax=800)