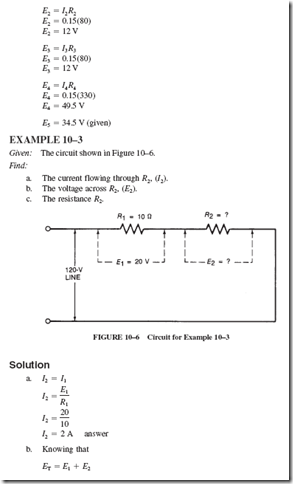
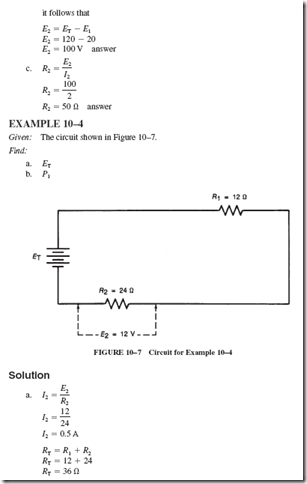
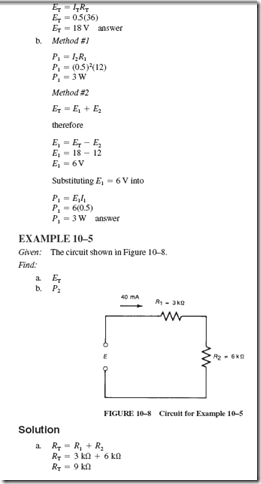
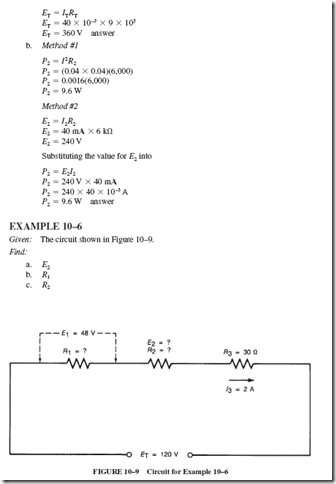
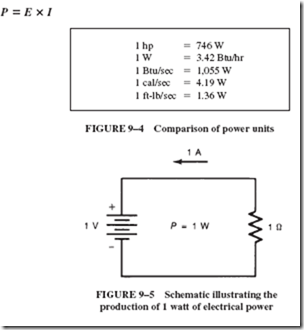
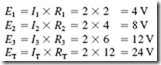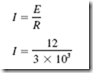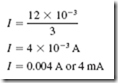9–4 ENERGY AND COST CALCULATIONS
Electrical energy is commercially sold in units called kilowatt-hours. The consumption of energy is not only a function of the power rating of the appliance, but also of
the amount of time for which it is employed. Obviously, it makes a difference on your electrical bill whether you burn a lamp for 1 hour or for 10 hours. Take, for instance, a 100-watt lightbulb. If you burn it for 1 hour, you have expended 100 watts 3 1 hour 5 100 watt-hours, which is equivalent to 0.1 kilowatt-hour (kWh). Burning it for 10 hours will require 10 times as much energy:

EXAMPLE 9–14
Given: Five 60-watt lamps and four 100-watt lamps burning daily for 5 hours.
Find: The cost of operating the lamps for a billing period of 30 days, at the cost of $0.056 per kilowatt-hour.
Solution

The Kilowatt-Hour Meter
The electrical energy delivered to consumers is measured by an instrument known as the kilowatt-hour meter. Such a meter generally has four dials geared to each other with a ratio of 10 to 1. Thus, when the unit dial makes ten revolutions, the tens dial makes one revolution. Similarly, the tens dial makes ten revolutions for every one revolution of the hundreds scale. The dials are driven by a small motor with a turning effect proportional to the product of voltage and current (E 3 I). The reading of each dial represents a whole number, with any fractional part of that number being found on the next lower dial.
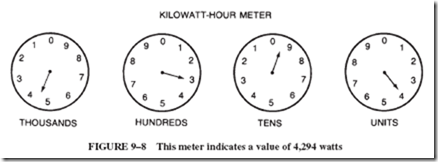
Figure 9–8 represents the four dials of such a kWh meter. In reading such a meter, some people start with the unit dial and then read from right to left; others read the dials from left to right, taking care to record the last number the pointer has passed. No matter how you do it, remember this:
If the pointer is between two digits, select the lower of the two numbers.
Put this knowledge to use and read the meter in Figure 9–8. If you do it correctly, the answer should be 4,294 kWh.
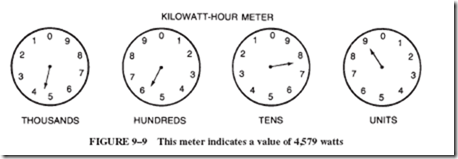
Now look at the dials in Figure 9–9. These dials represent the same meter read 1 month later. Do you agree that the new value is 4,579 kWh? By subtraction we find the difference between the two meter readings: 4,579 2 4,294 5 285 kWh. Thus, we have determined the amount of energy used during that month.
9–5 EFFICIENCY OF ENERGY CONVERSION
“Energy is never created (from nothing), and energy never vanishes” is one way of stating a principle long known as the law of conservation of energy. Each kilowatt- hour used comes from the burning of a fuel or from the release of some stored water. The energy of coal is still responsible for batteries used to light lamps; that is, coal is oxidized to release the zinc or lead used in the battery from other elements when the metal is refined. The electrical energy that we use daily is soon converted to heat by one process or another. Electrical energy can be stored briefly by charging batteries or
by pumping water into a storage tank. However, examples of energy storage are few. In general, energy is converted from one form to another. The efficiency of this energy conversion is a way of measuring how well the energy-converting device accomplishes its task.

EXAMPLE 9–15
Given: A DC motor taking 4.2 amperes on a 120-volt line and delivering 0.5 horsepower.
Find: The efficiency of the motor.
Solution
The power output is 0.5 hp, or 373 W (1 hp = 746 W).
The power input is 120 V x 4.2 A = 504 W.
The efficiency of the motor is 373/504 = 0.74 or 74%.
The efficiency of any device can be no greater than 100%. In other words, the device cannot give out more energy than it takes in. The efficiency of all electrical heating devices is 100%, because the electrical production of heat is easy. Heating devices may vary, however, in how effectively they deliver the heat from the coils in which it is produced to the place where it is to be used. In Example 9–15, we found that the motor is 74% efficient. The other 26% of the energy used appears as heat. If the motor stalls and produces no mechanical power, then 100% of the energy is converted to heat.
EXAMPLE 9–16
Given: An electrical generator with a 10-horsepower input producing 50 amperes at 100 volts.
Find: The efficiency of the generator.
Solution
Power output: 50 A x 100 V = 5,000 W
Power input: 10 hp = 7,460 W
Efficiency = 5,000/7,460 = 0.67 or 67%
You may ask yourself, “Can I drive an electrical generator with an electric motor and let the generated current run the motor?” The answer is, “This scheme will not work very well.” The reason is apparent from the previous discussion and Example 9–16. Both the motor and the generator waste some of the energy applied, with the result that one device is not going to produce enough energy to run the other device.
9–6 A PRACTICAL APPLICATION—RESISTANCE HEATING
The purpose of this section is twofold:
1. To encourage a review of theories and formulas covered up to this point, and
2. To demonstrate a practical application of many laws and formulas.
Most common heating devices, such as toasters, irons, and electric ranges, are heated by current in a coil of nickel-chromium alloy wire or ribbon. Electrical devices are widely used for localized production of small amounts of heat because of their ease of control. The appeal of nickel-chromium (nichrome, chromel, etc.) alloys lies in their small size and reasonable relationship of cost to durability.
To design a heavy-duty resistance-type soldering iron that develops heat at a rate of about 180 watts, consult Figure 9–10 for wire recommendations. Number 26-gauge wire might be used.
All the formulas necessary to complete the calculations have already been learned. The current in the wire is found from
Watts = Volts x Amperes
180 =120X
X = 1.5 A
|
Heater Watts (115 Volts)
|
Wire Gauge #
|
|
100–200
|
26–30
|
|
200–350
|
24–28
|
|
350–400
|
22–26
|
|
450–500
|
20–24
|
|
550–650
|
19–23
|
|
700–800
|
18–22
|
|
850–950
|
17–21
|
|
1,000–1,500
|
16–20
|
|
1,200–1,350
|
14–18
|
|
1,400–1,500
|
12–16
|
|
2,000
|
10–14
|
FIGURE 9–10 Nichrome wire recommendations
The resistance of the wire is found from Ohm’s law:

as shown in the section “Calculating the Resistance of a Wire” in Chapter 7. The value of K is 600, as specified in Figure 7–2, and the cross-sectional area A for #26 wire is given as 254 circular mils in the wire gauge table, Figure A–2 of the Appendix.
Rewriting the above equation for l, we obtain:

Assuming that the construction of a heating element with 33.8 feet of #26 wire would result in an element too large or too bulky for its application, a smaller and lighter element could be constructed using #28 wire instead. The same mathematical formula can be used to calculate the required length of #28 wire. The answer is that only 21.3 feet would be required instead of 33.8 feet. Thus it would appear that the use of #28 wire would be a superior choice because the heating coil would be smaller, lighter, and cheaper. However, there are trade-offs to be considered. When the required wattage is produced in a smaller volume of wire, the surface temperature of the wire is higher. Therefore, #28 wire will oxidize faster and have a shorter life.
Some heating appliances often use a heater element consisting of a coiled resistance wire enclosed in a steel tube. The space around the wire is packed with magnesium oxide, or similar filler, to insulate the wire from the protecting tube.
SUMMARY
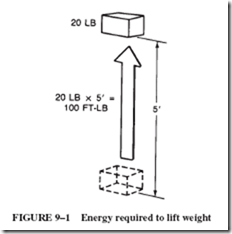
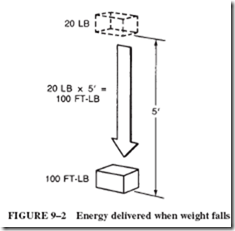
• Work 5 Force 3 Distance.
• Energy is the ability to do work.
• Power is the rate of using energy.
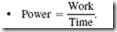
• Power x Time = Energy.
• Watts = Volts x Amperes.
• I2 R is synonymous with electrical power.
• Watts and kilowatts measure power, which is a rate.
• Watt-hours and kilowatt-hours measure energy.

Achievement Review
1. The word rate implies division by a unit of time. For example, the rate of speed for a car that travels 200 miles in 4 hours is 200 ÷ 4 or 50 miles per hour. Electric power, too, is defined as a rate. What is this definition?
2. A certain motor consumes 1,492 watts. What is the power rating in:
a. Horsepower?
b. Kilowatts?
3. If it were desired to obtain more light in a room, should a bulb with a smaller or greater wattage rating be used? Why?
4. What is meant by I2R losses?
5. What is the equation for finding P, if E and I are given?
6. What is the equation for finding E, if P and R are given?
7. What is the equation for finding I, if R and P are given?
8. What is the equation for finding R, if P and E are given?
9. Calculate the wattage for a 60-volt, 10-ampere arc lamp.
10. Find the power used by a 12-ampere, 110-volt heater.
11. What is the wattage rating of a 100-ohm resistor carrying 0.5 amperes?
12. Calculate the watts for a 2-ohm resistor on a 6-volt line.
13. Calculate resistance of a 60-watt, 120-volt lamp when operating.
14. Find operating current for an 800-watt, 115-volt toaster.
15. Find the cost of operating the toaster of question 14 for 5 hours per month if en- ergy costs $0.135 cents per kilowatt-hour.
16. A 4-ohm resistor is rated at 144 watts. What is the maximum current it can carry without burning up?
17. Another resistance is rated at 25 watts. This particular resistor has 400 ohms.
How much current can be pushed through this resistor before it might burn up?
18. A 750-watt electric iron, when connected to 120 volts, will take how much current?
19. How much current will flow through a wire supplying a 1-horsepower motor at 120 volts?
20. What would be the power, in watts, consumed if a heater rated at 7.5 amperes were connected to a 220-volt circuit?
21. A small pilot light is rated at 5.4 watts. What is the voltage needed to produce a current of 0.3 amperes?
22. How much will it cost to operate a washing machine for 15 hours a month if its motor is rated at 1⁄3 horsepower and the price of electric energy is $0.12 per kilowatt-hour? Assume 60% efficiency.
23. What is the resistance of a toaster whose label reads 1,200 W/120 V?
24. A long power transmission line suffers a power loss of 3.2 megawatts when 800 amperes are flowing through it. What is the resistance of the cable?
25. Two hundred forty milliamperes are flowing through a 4.7-kilohm resistance. What should be the minimum wattage rating of the resistor, including a 10% margin for safety?
26. A 6-volt battery is charged at the rate of 5 amperes for 24 hours. What is the amount of energy charge in kilowatt-hours?
27. One 1⁄4-horsepower DC motor is 70% efficient. What is the current through the motor, in amperes, when it is operating on a 120-volt line and delivering 1⁄4 horsepower?
28. A DC motor takes 5 amperes on a 110-volt line and is 60% efficient. Find the horsepower output. Find the heating rate in watts.
29. One pound of coal releases 12,000 Btu of energy when it is burned. What is this value expressed in foot-pounds?
30. If the energy of a pound of coal is converted into electrical energy (kilowatt- hours) by means of equipment that has an overall efficiency of 30%, what is the energy in kilowatt-hours obtained from a pound of coal?
31. Assuming that 50,000 Btu per hour are required to heat a house in cold weather, how many watts of electrical heat are needed to produce heat at this rate? (Electrical heat is 100% efficient.)
32. Calculate the power in watts that must be supplied to a 40-gallon electrical water heater to raise the temperature of a tank of water from 50°F to 150°F in 2 hours. Assume that no heat is wasted (1 gallon 5 81⁄3 lb). Calculate the cost of heating the water at $0.04 per kilowatt-hour.
33. Find the amount of time required for a 1,600-watt heating element to warm 30 gallons of water from 50°F to 150°F.
34. Find the time required to heat 1,900 grams of water (about 2 quarts) from 10°C to boiling (100°C) on a 660-watt hotplate.
35. Find the time required for the heating operation in question 34 if the process is 90% efficient; that is, only 90% of the heat input is delivered to the water.
36. The heating element of a 1,800-watt/120-volt hotplate has to be replaced. The heating coil will be made of nichrome, and the size of the wire must yield a maxi- mum life span.
a. How many ohms are required?
b. What size should the wire be?
c. How long should the wire be?
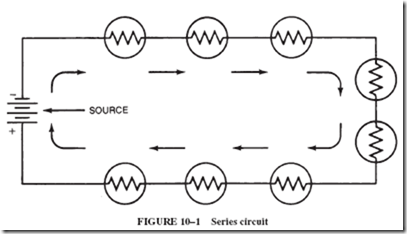
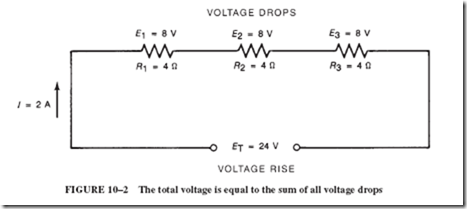
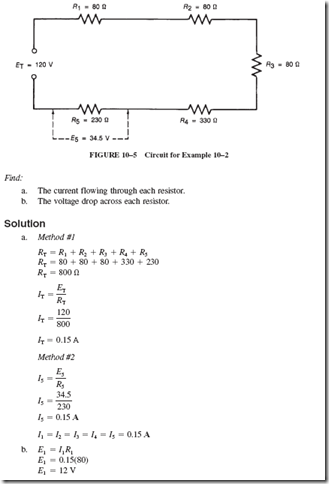
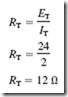 This may have been obvious to you right along. After all, if you add all the resistances in each circuit, you obtain the same result for RT, namely, 12 ohms. In other words,
This may have been obvious to you right along. After all, if you add all the resistances in each circuit, you obtain the same result for RT, namely, 12 ohms. In other words,