science universe

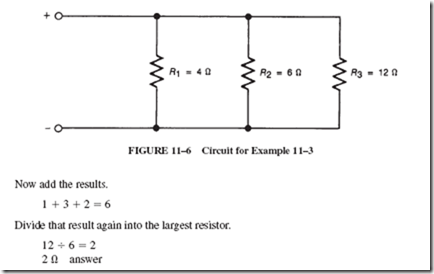
Conduction in Liquids and Gases

13–1 THE IONIZATION PROCESS

In solid conductors, the transfer of electrical charges is made by the movement of electrons. In liquids and gases, the transfer of electrical charges depends on particles

called ions. Ions were defined in Chapter 1 as atoms that have become electrically unbalanced by virtue of having lost or gained electrons.

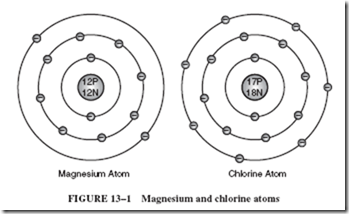
To briefly review this concept, consider the model of a magnesium atom alongside a chlorine atom, as shown in Figure 13–1.

You should recall that magnesium is classified as a metal because it has only two valence electrons. By contrast, chlorine gas has seven valence electrons and is, therefore, classified as a nonconductor.

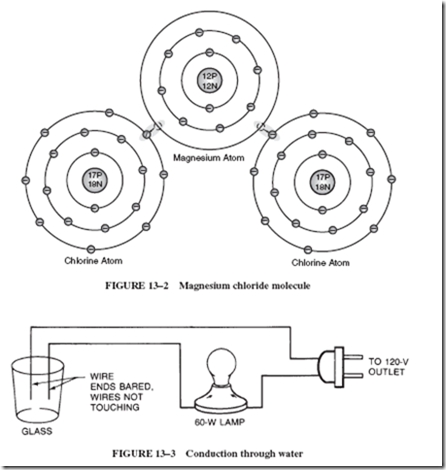
When a piece of magnesium is heated in the presence of chlorine gas, the two substances will chemically interact to form a new compound: a metallic salt called magnesium chloride. During this chemical process, each magnesium atom gives up its two valence electrons, which are then transferred to two neighboring atoms, as shown in Figure 13–2. These atoms are no longer known as atoms, since they now have been electrically charged. After an originally neutral atom becomes electrically charged, it is called an ion.

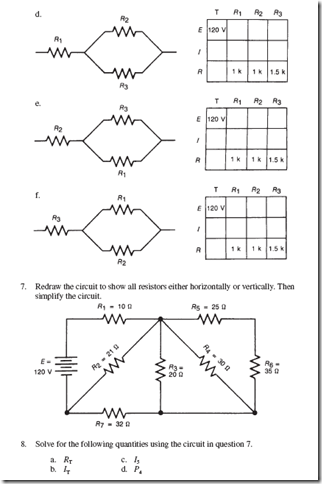
The magnesium atom has lost electrons (negative charges) and is now positively charged. Thus, it is called a positive ion. Likewise, the chlorine atoms have gained additional electrons and have been transformed into negative ions. Notice in Figure 13–2 that each ion has eight electrons in its outer shell.

This newly formed substance, magnesium chloride, is similar to table salt. The chemical name for table salt is sodium chloride; that is, the elements that make up table salt are a metal, sodium, and a nonmetal, chlorine.

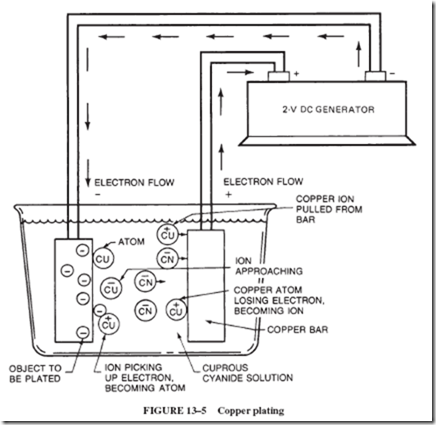
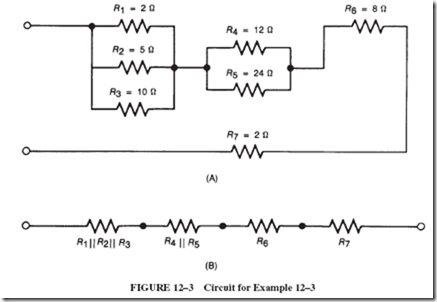
The conducting ability of a solution of salt in water can be demonstrated with the equipment shown in Figure 13–3. First, fill the glass with kerosene, and then connect the circuit to the 120-volt line. Nothing happens to the lamp as a result of this step. Now add some table salt or magnesium chloride to the kerosene. The neutral molecules of the kerosene do not attract the undissolved charged ions of the salt. Again, there is no current through the lamp.

Fill another glass with pure distilled water (if available) and connect the circuit. Note that nothing happens. If water from the faucet is used in the glass, the lamp may light very dimly. When salt is added to the water and is stirred to dissolve, the lamp brightens. What causes this increased conductivity when magnesium chloride or sodium

chloride is dissolved in water? The dissolved substance does not retain its molecular structure but breaks up into its ion particles, which are free to move through the liquid.

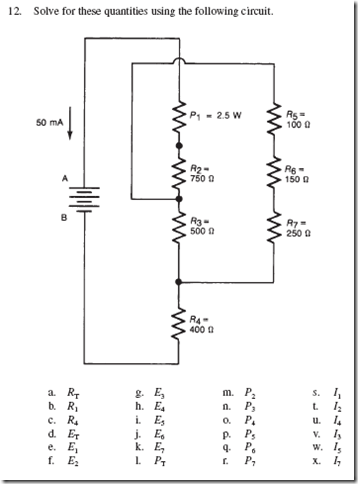
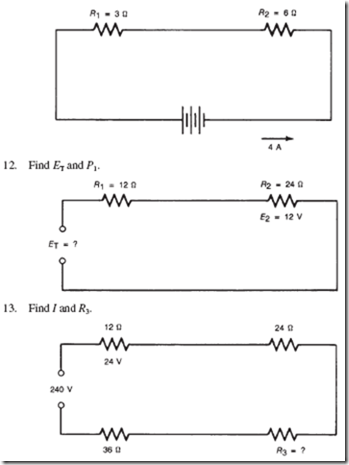
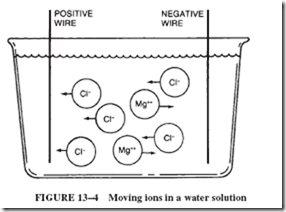
Figure 13–4 shows a water solution consisting of negative chlorine ions and positive magnesium ions. When two electrically charged wires are submerged into the solution, a two-way movement of ions takes place. The negative chlorine ions are being attracted by the positive wire, and the positive magnesium ions are pulled toward the negative wire. When the ions reach their respective wires, the resulting action depends on the kinds of ions and the type of wire used.

In this manner, water solutions of acids, bases, and metallic salts can conduct large amounts of current. Such solutions are known as electrolytes.

The following points summarize the information presented so far:

• Metals and nonmetals unite to form compounds by transferring electrons from the metallic atoms to the nonmetallic atoms.

• As a result of the electron transfer, the compound consists of positively charged metallic

ions and negatively charged nonmetallic ions.

• Some compounds dissolve in water and dissociate; that is, the ions become separated and move freely. Ions are much larger and heavier than electrons.

• Conduction in metals consists of the movement of free (negative) electrons.

• Conduction in solutions, known as electrolytes, consists of the movement of free positive and negative ions in opposite directions.

13–2 USEFUL CHEMICAL COMPOUNDS

The ions covered so far are formed by the electrical charging (either positive or negative) of a single atom. More complicated ions, however, do exist. These ions consist of charged groups of atoms. The following four compounds, each of which is useful in electrical processes, are formed, in part, of these larger ions.

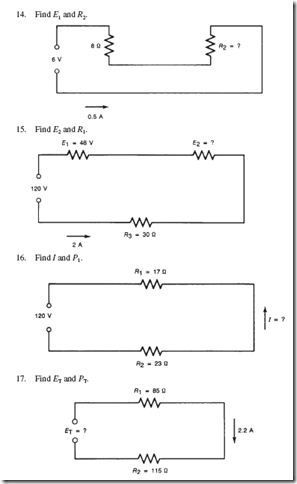
Sulfuric Acid. This compound is used as the electrolyte in automobile batteries. The chemical formula for sulfuric acid is H2SO4. In other words, one molecule of the acid contains two atoms of hydrogen, one atom of sulfur, and four atoms of oxygen. When mixed with water, each molecule can separate into the ions shown: H1 H1 SO422. The 1 sign on the H indicates a hydrogen ion (a hydrogen atom that has lost its one electron). The is called a sulfate ion and consists of one sulfur atom, four oxygen atoms, and two extra electrons. (Notice that an ion can be either one electrically charged atom or a group of such atoms.) The two electrons are necessary to hold the SO4 group together. The electrons are part of an electron-sharing arrangement that keeps the electron rings of the sulfur and oxygen atoms tied together.

Ammonium Chloride. The electrolyte in a dry cell is a solution of ammonium chloride dissolved in water. Pure ammonium chloride is a white solid. The formula for ammonium

chloride is NH4Cl. Ammonium chloride separates into two ions when it dissolves: NH41 and Cl2. The symbol NH41 means that one nitrogen atom and four hydrogen atoms are grouped together with the loss of one electron. The electron lost by the NH4 group is taken by the chlorine atom to form a negatively charged chlorine ion. The NH41 group is called an ammonium ion.

Cuprous Cyanide. The commercial process of electroplating copper on iron uses a poi- sonous solid called cuprous cyanide as the plating solution. The formula for cuprous cyanide is CuCN. In solution, the compound separates into the ions Cu1 and CN2. Cu is the symbol for copper. Cu1 represents the cuprous ion (a copper atom that has lost its outer- most electron). CN2 is one atom of carbon and one atom of nitrogen held together with the help of one electron taken from the copper atom. CN2 is called the cyanide ion.

Copper Sulfate. Some copper-plating processes use a copper compound called copper sulfate, CuSO4. Copper sulfate is a solid in the form of blue crystals. When copper sulfate dissolves in water, it forms Cu11 and SO422 ions. Under some conditions, a copper atom can lose two of its electrons to form an ion called a cupric ion. SO422 is the same sulfate ion that appears in sulfuric acid.

13–3 ELECTROPLATING AND ELECTROLYSIS

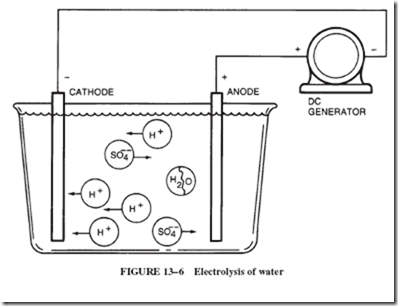
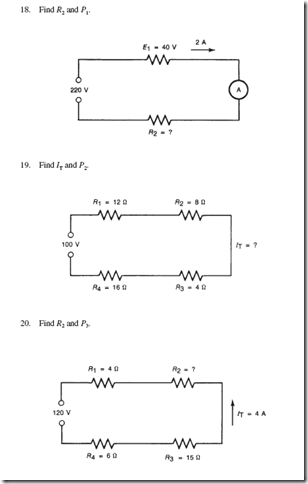
To illustrate the electrical process that occurs in the plating of metals, let us examine the plating of an object with copper from a cyanide solution. The object to be plated, Figure 13–5, must be an electrical conductor. It is connected to the negative terminal of a battery or DC generator and is covered by the cuprous cyanide solution. The positive terminal of the supply is connected to a copper bar, which is also covered by the solution. When the circuit is complete, positively charged copper ions in the liquid move toward the object to be plated. When the copper ions touch the negatively charged object, the ions pick up electrons and become neutral atoms of copper. As the ions become atoms at the surface of the negatively charged object, they form a copper coating over the object. As long as the generator pushes electrons onto the object to be plated so that its negative charge is maintained, a copper coating of increasing thickness will be deposited on the object.

When the cyanide ions hit the positive copper bar, copper atoms on the surface of the bar lose electrons and become ions. In other words, the negative CN ion causes a copper atom to lose an electron and become a positive ion. The copper ion is attracted into the solution by the negative ions present in the solution. The electrons lost by the copper atoms drift toward the generator. Just as many copper ions are liberated from the copper bar as are de- posited on the object to be plated; therefore, the solution stays at a constant strength.

In any electroplating process, the solution must contain the ions of the metal that is to form the coating. Since metal ions are all positively charged, the object to be plated is connected to the negative wire. The positive terminal normally is made of the same metal that is to form the coating. Plating solutions also contain ingredients other than the dissolved metal compound. These other ingredients are added to prevent corrosion of the object to be plated, to prevent poisonous fumes, and to aid in forming a smooth coating.

The purification of metals can be accomplished through a large-scale plating process. Almost all commercial copper is refined by plating in a copper sulfate solution.

Pure copper is deposited on the negative plate. Impurities from the crude copper on the positive terminal either stay in the solution or never leave the copper bar at all. Impure copper has a high resistance. Copper wire manufacturers require electrolytically purified copper in the production of low-resistance conductor wire. Zinc and other metals are purified in a similar fashion.

The term electrolysis refers to the process of separating elements by the use of electrical energy. The commercial production of metallic and nonmetallic elements is often a matter of separating the element from others with which it is chemically combined. In 1885, aluminum was a rare and precious metal because it was difficult to separate from its abundant compound, aluminum oxide. Aluminum metal became inexpensive when a process was discovered for separating the aluminum from the oxygen. The extraction of aluminum is an electrical process in which electrons are removed from oxygen ions and are returned to aluminum ions. Magnesium metal is extracted from magnesium chloride (from seawater) by electrically separating the magnesium ions from the chlorine ions.

One process that has an important application in batteries is the electrolysis of water containing sulfuric acid. Hydrogen and oxygen gases are produced in this process; however, the commercial production of large amounts of these gases is achieved more economically by other processes.

Electrolysis of Sulfuric Acid in Water

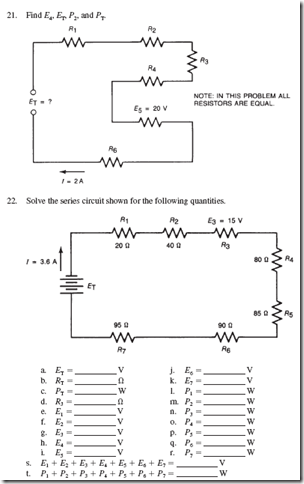
Two new terms are shown in Figure 13–6: the cathode is the terminal or electrode where electrons enter the cell, and the anode is the electrode that carries electrons away from the cell.

Assume that the cathode and anode are made of materials that are not affected by the sulfuric acid solution or by the hydrogen or oxygen released in the process. When hydrogen ions touch the cathode, they pick up electrons from it and become neutral atoms. These atoms of hydrogen form hydrogen gas, which escapes from the solution as bubbles. When the sulfate ions approach the anode, they cause the water molecules to break up. The positive anode requires electrons, and the water molecules part with electrons more readily than the SO422 ions. Therefore, the removal of two electrons from the H2O molecule leaves two H1 ions and one oxygen atom. The oxygen atoms bubble away as gas at the anode, and the H1 ions stay in the solution. For each pair of hydrogen ions formed at the anode, a pair of hydrogen ions is discharged as gas at the cathode. The amount of acid in the solution remains constant, and the water is gradually consumed.

If lead plates are used for the cathode and anode, then not all of the oxygen bubbles away. A portion of the oxygen combines with the lead anode to form lead dioxide. The hydrogen does not affect the cathode, which remains as pure lead.

Applications of plates of lead and lead dioxide in a solution of sulfuric acid relates to the working principles of storage batteries. More detailed information about this principle is offered in Section 14–5.

Electrolytic Corrosion

Corrosion is the rusting or wearing away of a metal by the formation of a chemical compound of the metal. In some instances, the corrosion process is desirable. For example, in copper plating, the copper anode dissolves and in that way maintains the necessary copper ions in the plating solution. An example of an undesirable type of corrosion is shown when there is an electrical current through the earth that can follow buried water pipes for a portion of its path. At any points where the buried metal is positive (anodic) as compared to the earth, the attack on the pipe by negative ions converts the metal atoms into metal ions; in other words, iron pipe is converted into iron rust.

12–3 KIRCHHOFF’S CURRENT LAW

Consider a junction of three wires, called a node, as shown in Figure 12–9. Information is given concerning the amount and direction of the current in only two of the wires. With this information, however, it is possible to deduce the amount and direction of the unknown current in the third wire. This is what Kirchhoff’s current law is all about. This law can be stated as follows:

At any node, the algebraic sum of the currents equals zero.

You have probably reasoned already that, in Figure 12–9A, a current of 2 amperes is flowing from left to right, and in Figure 12–9B, a current of 8 amperes is flowing from left to right. It appears that the total amount of current flowing into a junction must equal the current coming out. In short: What goes in must come out.

To apply Kirchhoff’s current law, we arbitrarily assign positive direction to currents flowing into the junction and negative direction to currents coming out of the juncion. If X denotes the unknown quantity, it follows that for Figure 12–9A

Remember, the negative sign of the answer denotes the current flowing away from the junction.

The following example is designed to demonstrate the usefulness of Kirchhoff’s volt- age and current laws in the solution of complex circuits.

EXAMPLE 12–6

Given: The circuit shown in Figure 12–10.

Find: All voltage drops, all resistance values, and all branch currents that are not given.

Solution

Note: Remember, our aim is to find all branch currents.

Applying the principles of Kirchhoff ’s current law, the following facts can be confirmed.

• The 8-ampere current entering node A divides in such manner that 3 amperes will flow upward (from A to B) through R8.

• The power source provides a line current of 8 amperes to the circuit. The same 8-ampere current returns to the power source through R1. Therefore, I1 5 8 amperes.

• At point B the current I8 combines with the current I2 to constitute the 8-ampere line current leaving point B toward the left. This implies that I2 must be equal to 5 amperes.

• Knowing that I2 5 5 amperes and I3 5 3 amperes, it follows that I9, flowing from D to C, equals 2 amperes.

• This completes all the computations for the different branch currents. We suggest that you enter the new information into your diagram, as shown in Figure 12–10.

Using Ohm’s law, we can now find the voltage drops of the first loop as follows:

12–4 LOADED VOLTAGE DIVIDERS

At this time you should have a complete understanding of simple voltage dividers, which were covered in Chapter 10. A brief review of Sections 10–8 through 10–11 is highly recommended before proceeding with this section.

To understand the concept of loaded voltage dividers, consider the following hypothetical problem.

Let us assume you own a small portable radio that requires a 9-volt battery. All you have available is a 12-volt battery and a few resistors, so you decide to construct a voltage divider like the one shown in Figure 12–11. The values of the resistors are chosen in a ratio of 1 to 3; therefore, the supply voltage will be divided in a like ratio and you have your desired 9-volt supply, or so you think.

But watch what happens when you connect your radio across terminals A and B. Your radio, too, has a resistance, say 30 kilohms. When you connect the radio across the 60-kilohm resistor, you have a parallel circuit from A to B with an equivalent resistance of 20 kilohms. Now your voltage division is in a ratio of only 1 to 1, and your radio receives only 6 volts instead of the anticipated 9 volts. The radio has loaded the voltage divider. In other words, simple (unloaded) voltage dividers are series circuits, while loaded voltage dividers represent series-parallel circuits.

Note: The word load refers, of course, to any device that draws current from the voltage divider. That much is probably obvious to you. What may be new is the fact that

A small resistance is a big load and a large resistance represents a small load.

You see, the nominal size of a load is determined by the current it draws, not by its resistance value. Knowing this, you may appreciate the fact that the output from a voltage divider changes with varying load conditions. This f luctuation of voltage output is referred to as voltage regulation.

A high percentage of voltage regulation is undesirable and can be improved by minimizing the value of the so-called bleeder resistor. The bleeder is defined as that portion of the voltage divider that is connected parallel to the load.

The design of a voltage divider begins with choosing the size of the bleeder resistor so that it will draw at least 10% of the load current. An example will illustrate this.

EXAMPLE 12–7

Given: A power source of 240 volts and a load that draws 60 milliamps at 150 volts, as shown in Figure 12–12.

Find: The proper resistance values of the voltage divider.

SUMMARY

• Series-parallel circuits can be redrawn in a simplified form by substituting equivalent resistors for parallel and series combinations.

• Kirchhoff’s voltage law states that the algebraic sum of voltages around any closed

loop equals zero.

• Kirchhoff’s current law states that the algebraic sum of currents at a node equals zero.

• Practical voltage dividers are series-parallel circuits whose resistance values are determined by the load(s).

• Heavy loads are characterized by a low resistance, and small loads are characterized by high resistance.

• Low-value bleeder resistors improve the voltage regulation of voltage dividers.

Achievement Review

1. Solve for these quantities using the following schematic.

.

9. Solve the following circuit to find all voltage drops and all the currents. Sug- gested sequence of operations:

a. Find RT and IT.

b. Apply Kirchhoff’s and Ohm’s laws to find unknown.

c. Enter all your answers in the drawing. (It helps to use different colors.)

d. Confirm your results by adding voltages around each loop.

10. Find

a. The total resistance of the circuit.

b. The voltage drop across A–B.

c. The current in the branch A–D–C.

d. The potential difference between B and D.

Series-Parallel Circuits and Loaded Voltage Dividers

12–1 SIMPLIFYING SERIES-PARALLEL CIRCUITS

Pure series circuits and pure parallel circuits are seldom encountered in the practical applications of electricity and electronics. It is more common to deal with circuits that combine the aspects of both.

This chapter will introduce you to seemingly complicated circuit problems that may be solved by the same principles you have learned in the last two chapters. These principles can be summarized as follows:

In series circuits, current is the same; voltages add. In parallel circuits, voltage is the same; currents add.

There is no one formula that can be applied to an entire circuit to obtain the desired answer or answers. Ohm’s law must be applied first to one part of the circuit and then to another part. This procedure will lead from what we know to what we need to find.

EXAMPLE 12–1

Given: The circuit shown in Figure 12–1A.

Find: The total circuit resistance..

Solution

a. Identify all parallel combinations and solve for their equivalent resistance values.

Note the symbols R2 7 R3 and R4 7 R5 used to identify these values.

The symbol 7 means “the parallel combination of.” In the computation here, R2 7 R3 is a symbolic way of saying “the equivalent resistance of the parallel combination of R2 and R3.”

b. Redraw the circuit with the computed equivalent values, as shown in Figure 12–1B.

c. Redraw the circuit as a single resistance, as shown in Figure 12–1C.

EXAMPLE 12–2

Given: The circuit shown in Figure 12–2A.

Find: The total circuit resistance.

Solution

Note: R4 is not in parallel with R2 as it may seem upon casual inspection. Instead, it is the series combination of R3 and R4 that is connected parallel to R2. The result is a single parallel circuit with an equivalent resistance of 2.73 ohms.

EXAMPLE 12–3

Given: The circuit shown in Figure 12–3A.

Find: The total circuit resistance..

Solution

Note: The parallel combinations have been identified for you, and the circuit has been redrawn accordingly, as shown in Figure 12–3B. Now it is your task to compute the equivalent values and to finish the problem. The answer is 19.25 ohms.

EXAMPLE 12–4

Given: The circuit shown in Figure 12–4.

Find: The total circuit resistance.

Solution

Once again, the parallel combinations have been identified for you, and the circuit should be redrawn accordingly. Finish it! The answer is 50 ohms.

EXAMPLE 12–5

Given: The circuit shown in Figure 12–5.

Find:

a. The total circuit resistance R_T.

b. The current from A to B.

c. The current from C to D.

d. The total current supplied.

e. Each voltage drop across the resistors.

12–2 KIRCHHOFF’S VOLTAGE LAW

We will now use Example 12–5 to develop the ideas expressed by Kirchhoff’s voltage law, which states:

Around any closed loop, the algebraic sum of the voltages is equal to zero.

Or, as some people prefer it:

Around any closed loop, the sum of the voltage drops is equal to the sum of the voltage rises.

Note that one key phrase is common to both statements, namely: “Around any closed loop . . .”

The problem of Example 12–5 has three closed loops, as shown in Figure 12–8.

Recall our convention of determining the polarity of a voltage drop. This was fully explained in Section 10–9, which you may have to review before you continue.

Tracking the loops in a clockwise direction, we obtain the following information:

This, indeed, confirms Kirchhoff’s voltage law. Incidentally, the note at the conclusion of Example 12–5 is another statement confirming the truth of Kirchhoff’s voltage law.

Series-Parallel Circuits and Loaded Voltage Dividers

12–1 SIMPLIFYING SERIES-PARALLEL CIRCUITS

Pure series circuits and pure parallel circuits are seldom encountered in the practical applications of electricity and electronics. It is more common to deal with circuits that combine the aspects of both.

This chapter will introduce you to seemingly complicated circuit problems that may be solved by the same principles you have learned in the last two chapters. These principles can be summarized as follows:

In series circuits, current is the same; voltages add. In parallel circuits, voltage is the same; currents add.

There is no one formula that can be applied to an entire circuit to obtain the desired answer or answers. Ohm’s law must be applied first to one part of the circuit and then to another part. This procedure will lead from what we know to what we need to find.

EXAMPLE 12–1

Given: The circuit shown in Figure 12–1A.

Find: The total circuit resistance..

Solution

a. Identify all parallel combinations and solve for their equivalent resistance values.

Note the symbols R2 7 R3 and R4 7 R5 used to identify these values.

The symbol 7 means “the parallel combination of.” In the computation here, R2 7 R3 is a symbolic way of saying “the equivalent resistance of the parallel combination of R2 and R3.”

b. Redraw the circuit with the computed equivalent values, as shown in Figure 12–1B.

c. Redraw the circuit as a single resistance, as shown in Figure 12–1C.

EXAMPLE 12–2

Given: The circuit shown in Figure 12–2A.

Find: The total circuit resistance.

Solution

Note: R4 is not in parallel with R2 as it may seem upon casual inspection. Instead, it is the series combination of R3 and R4 that is connected parallel to R2. The result is a single parallel circuit with an equivalent resistance of 2.73 ohms.

EXAMPLE 12–3

Given: The circuit shown in Figure 12–3A.

Find: The total circuit resistance..

Solution

Note: The parallel combinations have been identified for you, and the circuit has been redrawn accordingly, as shown in Figure 12–3B. Now it is your task to compute the equivalent values and to finish the problem. The answer is 19.25 ohms.

EXAMPLE 12–4

Given: The circuit shown in Figure 12–4.

Find: The total circuit resistance.

Solution

Once again, the parallel combinations have been identified for you, and the circuit should be redrawn accordingly. Finish it! The answer is 50 ohms.

EXAMPLE 12–5

Given: The circuit shown in Figure 12–5.

Find:

a. The total circuit resistance R_T.

b. The current from A to B.

c. The current from C to D.

d. The total current supplied.

e. Each voltage drop across the resistors.

12–2 KIRCHHOFF’S VOLTAGE LAW

We will now use Example 12–5 to develop the ideas expressed by Kirchhoff’s voltage law, which states:

Around any closed loop, the algebraic sum of the voltages is equal to zero.

Or, as some people prefer it:

Around any closed loop, the sum of the voltage drops is equal to the sum of the voltage rises.

Note that one key phrase is common to both statements, namely: “Around any closed loop . . .”

The problem of Example 12–5 has three closed loops, as shown in Figure 12–8.

Recall our convention of determining the polarity of a voltage drop. This was fully explained in Section 10–9, which you may have to review before you continue.

Tracking the loops in a clockwise direction, we obtain the following information:

This, indeed, confirms Kirchhoff’s voltage law. Incidentally, the note at the conclusion of Example 12–5 is another statement confirming the truth of Kirchhoff’s voltage law.

11–4 VOLTAGE SOURCES IN PARALLEL

Voltage sources, such as batteries and generators, can be interconnected in a parallel arrangement in order to increase the current output capability. Voltage sources connected in parallel must have the same voltage rating, and care must be taken to match the polarities—positive to positive and negative to negative.

Figure 11–11 shows three 12-volt batteries properly connected in a parallel arrangement. Compare this with the series connection described in the summary to Chapter 10, and note that the parallel connection involves one voltage only.

The advantage gained with a parallel connection is based on current considerations. For example, if each battery in this illustration is capable of delivering 100 amperes of current, it is true that three batteries in parallel can deliver as much as 300 amperes. This is the same as saying that the system can deliver three times more power, or watts, than can be obtained from one battery alone. In the event that the current demand is limited to 100 amperes, the battery system would last three times as long as would one battery before it needed to be replaced or recharged.

11–5 A PRACTICAL APPLICATION—KITCHEN RANGE HEATING ELEMENT

Note: In the past, earlier designs of kitchen range heating elements lent themselves well to a demonstration of the use of series and parallel connections with a dual-voltage source.

Dual Voltage and the Three-Wire Supply

It is commonly assumed that American household appliances operate on 120 volts. However, it is economically advantageous to operate larger heating devices, such as electric kitchen ranges, water heaters, clothes dryers, and high-Btu air conditioners on a higher

voltage, namely, 240 V. Since power is equal to the product of voltage and current (P 5 E 3 I), it stands to reason that by doubling the voltage we cut the current in half. This makes for great savings of resources because with only half the current, the circuit wiring can be installed with smaller conductors.

The common distribution system brings two voltages on three wires into a home. Figure 11–12 illustrates such a system as if it came from two series-connected generators. Each generator develops 120 volts; the two in series give 240 volts. The two outside wires at top and bottom provide the 240-volt supply for ranges and large heaters. The middle wire, in practice, is grounded securely to a cold-water pipe. The neutral wire carries only the difference in current carried by the two outside wires and therefore need not be as large as the outside wires.

These relationships of voltages and currents hold true whether the source voltage is DC or AC. On alternating current, the two circles marked G in Figure 11–12 represent the two halves of a 240-volt winding on a distribution transformer that supplies AC energy to a house. Such a wiring arrangement for AC is called three-wire, single-phase.

The Range Top Heating Element

Electric ranges connect to the neutral as well as to the 240-volt wires, thus pro- viding a dual voltage. It will be shown that this voltage of 120/240 V can be applied many different ways to a heating element similar to the one shown in Figure 11–13. Notice that this heating element is composed of two series-connected resistors with three terminals. With both 120 and 240 volts available, a multiple-contact switch allows as many as eight different heating rates to be obtained from various combinations of voltages on the two resistors of the cooking unit.

For example, one manufacturer uses a six-position switch to obtain five different heat settings from the two heater elements in Figure 11–13, as follows:

You are encouraged to confirm the information above by making the appropriate calculations.

11–6 CURRENT DIVIDERS

All parallel circuits are current dividers. As discussed previously, the sum of the currents through each branch must equal the total circuit current. More current will flow through a branch having a low resistance than a branch having a high resistance. The amount of current flowing through each branch is inversely proportional to the resistance of that branch.

In a parallel circuit, the voltage across each branch is the same. Therefore, the cur- rent flow through any branch can be computed by dividing the source voltage (ET) by the resistance of that branch.

EXAMPLE 11–8

Three resistors having values of 40 ohms, 60 ohms, and 120 ohms are connected in parallel. The total circuit current is 3 amperes. Find the current through each branch using the current divider formula.

Solution

First find the total circuit resistance.

SUMMARY

• There is only one voltage in parallel circuits.

• In parallel circuits, each device has its own current, which is independent of other devices.

• In parallel circuits, the total current is equal to the sum of all the individual branch currents.

• In parallel circuits, the total circuit resistance is always smaller than any of the branch resistors.

• The total resistance of a parallel circuit can be calculated by the reciprocal formula.

• Parallel circuits with only two resistors can be solved by the product over the sum equation.

• Parallel circuits with all equal resistors have a total circuit resistance equal to the value of one resistor divided by the number of branches.

• Voltage sources in parallel must have the same voltage rating.

• Voltage sources in parallel can yield more current and increased power output.

• The current divider formula can be used to determine the current through each branch of a parallel circuit.

Achievement Review

1. Determine the total resistance of a 5-ohm resistor and a 15-ohm resistor connected in parallel.

2. Four 12-ohm resistors are connected in parallel. Calculate the total circuit resistance.

3. A 4-ohm, 12-ohm, and 16-ohm resistor are connected in parallel. Calculate the total circuit resistance by using the reciprocal formula.

4. The group of resistors mentioned in question 3 is connected in parallel across a 120-volt DC supply. Calculate the current through each resistor. Find the total current and the total circuit resistance by applying Ohm’s law.

5. Five lamps of equal resistance are connected in parallel across a 120-volt line.

If the total current supplied measures 3 amperes, what is the resistance of each

lamp?

6. The combined resistance (RT) of two lamps in parallel is 35 ohms. If the resistance of one lamp is 105 ohms, what is the resistance of the other?

7. Three equal resistors are connected in series and have a total resistance of 45 ohms. What would be their combined resistance if they were connected in parallel?

8. Find R1 and RT.

18. Show, by calculation, how eight different heating rates can be obtained from a heating element, as shown in Figure 11–13, consisting of two resistors in series with values of 50 ohms and 65 ohms, respectively.

11–4 VOLTAGE SOURCES IN PARALLEL

Voltage sources, such as batteries and generators, can be interconnected in a parallel arrangement in order to increase the current output capability. Voltage sources connected in parallel must have the same voltage rating, and care must be taken to match the polarities—positive to positive and negative to negative.

Figure 11–11 shows three 12-volt batteries properly connected in a parallel arrangement. Compare this with the series connection described in the summary to Chapter 10, and note that the parallel connection involves one voltage only.

The advantage gained with a parallel connection is based on current considerations. For example, if each battery in this illustration is capable of delivering 100 amperes of current, it is true that three batteries in parallel can deliver as much as 300 amperes. This is the same as saying that the system can deliver three times more power, or watts, than can be obtained from one battery alone. In the event that the current demand is limited to 100 amperes, the battery system would last three times as long as would one battery before it needed to be replaced or recharged.

11–5 A PRACTICAL APPLICATION—KITCHEN RANGE HEATING ELEMENT

Note: In the past, earlier designs of kitchen range heating elements lent themselves well to a demonstration of the use of series and parallel connections with a dual-voltage source.

Dual Voltage and the Three-Wire Supply

It is commonly assumed that American household appliances operate on 120 volts. However, it is economically advantageous to operate larger heating devices, such as electric kitchen ranges, water heaters, clothes dryers, and high-Btu air conditioners on a higher

voltage, namely, 240 V. Since power is equal to the product of voltage and current (P 5 E 3 I), it stands to reason that by doubling the voltage we cut the current in half. This makes for great savings of resources because with only half the current, the circuit wiring can be installed with smaller conductors.

The common distribution system brings two voltages on three wires into a home. Figure 11–12 illustrates such a system as if it came from two series-connected generators. Each generator develops 120 volts; the two in series give 240 volts. The two outside wires at top and bottom provide the 240-volt supply for ranges and large heaters. The middle wire, in practice, is grounded securely to a cold-water pipe. The neutral wire carries only the difference in current carried by the two outside wires and therefore need not be as large as the outside wires.

These relationships of voltages and currents hold true whether the source voltage is DC or AC. On alternating current, the two circles marked G in Figure 11–12 represent the two halves of a 240-volt winding on a distribution transformer that supplies AC energy to a house. Such a wiring arrangement for AC is called three-wire, single-phase.

The Range Top Heating Element

Electric ranges connect to the neutral as well as to the 240-volt wires, thus pro- viding a dual voltage. It will be shown that this voltage of 120/240 V can be applied many different ways to a heating element similar to the one shown in Figure 11–13. Notice that this heating element is composed of two series-connected resistors with three terminals. With both 120 and 240 volts available, a multiple-contact switch allows as many as eight different heating rates to be obtained from various combinations of voltages on the two resistors of the cooking unit.

For example, one manufacturer uses a six-position switch to obtain five different heat settings from the two heater elements in Figure 11–13, as follows:

You are encouraged to confirm the information above by making the appropriate calculations.

11–6 CURRENT DIVIDERS

All parallel circuits are current dividers. As discussed previously, the sum of the currents through each branch must equal the total circuit current. More current will flow through a branch having a low resistance than a branch having a high resistance. The amount of current flowing through each branch is inversely proportional to the resistance of that branch.

In a parallel circuit, the voltage across each branch is the same. Therefore, the cur- rent flow through any branch can be computed by dividing the source voltage (ET) by the resistance of that branch.

EXAMPLE 11–8

Three resistors having values of 40 ohms, 60 ohms, and 120 ohms are connected in parallel. The total circuit current is 3 amperes. Find the current through each branch using the current divider formula.

Solution

First find the total circuit resistance.

SUMMARY

• There is only one voltage in parallel circuits.

• In parallel circuits, each device has its own current, which is independent of other devices.

• In parallel circuits, the total current is equal to the sum of all the individual branch currents.

• In parallel circuits, the total circuit resistance is always smaller than any of the branch resistors.

• The total resistance of a parallel circuit can be calculated by the reciprocal formula.

• Parallel circuits with only two resistors can be solved by the product over the sum equation.

• Parallel circuits with all equal resistors have a total circuit resistance equal to the value of one resistor divided by the number of branches.

• Voltage sources in parallel must have the same voltage rating.

• Voltage sources in parallel can yield more current and increased power output.

• The current divider formula can be used to determine the current through each branch of a parallel circuit.

Achievement Review

1. Determine the total resistance of a 5-ohm resistor and a 15-ohm resistor connected in parallel.

2. Four 12-ohm resistors are connected in parallel. Calculate the total circuit resistance.

3. A 4-ohm, 12-ohm, and 16-ohm resistor are connected in parallel. Calculate the total circuit resistance by using the reciprocal formula.

4. The group of resistors mentioned in question 3 is connected in parallel across a 120-volt DC supply. Calculate the current through each resistor. Find the total current and the total circuit resistance by applying Ohm’s law.

5. Five lamps of equal resistance are connected in parallel across a 120-volt line.

If the total current supplied measures 3 amperes, what is the resistance of each

lamp?

6. The combined resistance (RT) of two lamps in parallel is 35 ohms. If the resistance of one lamp is 105 ohms, what is the resistance of the other?

7. Three equal resistors are connected in series and have a total resistance of 45 ohms. What would be their combined resistance if they were connected in parallel?

8. Find R1 and RT.

18. Show, by calculation, how eight different heating rates can be obtained from a heating element, as shown in Figure 11–13, consisting of two resistors in series with values of 50 ohms and 65 ohms, respectively.

Parallel Circuits

11–1 THE NATURE OF PARALLEL CIRCUITS

You should recall that series circuits were defined as having one, and only one, path along which the current can flow. By contrast, a parallel circuit has more than one path through which the current can flow. Figure 11–1 is such a parallel circuit. This is the standard representation where all resistors are drawn parallel to one another, resembling the ties between railroad tracks.

Now look at the two schematics in Figure 11–2, which are representations of the same parallel circuit shown in Figure 11–1. The common feature of these parallel circuits can be detected by carefully tracing each possible current path. Then it will become clear that each individual resistor is connected to the negative and positive pole of the battery. If you have difficulty in perceiving this fact, trace the negative and positive supply lines with two different-colored pencils from the source to each resistor.

What all these drawings convey is the fact that there is only one voltage serving all load resistors. (Compare this with the characteristics of a series circuit, where every resistor may have a different voltage drop.) Mathematically stated,

Also, as you trace the current path from its power source, you will notice that the current divides at some junction point, flows through the individual branch resistors, and then recombines at some other junction point before it returns to the power source.

Now, carefully check the three drawings just mentioned. They all show identical current flow to demonstrate that the total line current (supplied by the source) is equal to the sum of all the individual branch currents. (Compare this with the characteristics of a series circuit, where we dealt with one common current in each part of the circuit.) Mathematically stated,

We have compared the voltage and current distribution of parallel circuits with that of series circuits. Now it is time to compare the total resistance of such circuits.

In a series circuit, as you should recall, the total resistance increases with every additional resistance. In parallel circuits, by contrast, we encounter exactly the opposite.

In other words, the total resistance of a parallel circuit decreases whenever additional resistors are connected to the circuit. In fact, the total resistance is always smaller than any of the individual branch resistors.

There are five different methods by which the total resistance of a parallel circuit may be computed. How to employ these methods will be the subject of the next few sections.

11–2 FIVE METHODS OF COMPUTATION

Method #1: Use of Ohm’s Law for Computing RT

An easy way of determining the total resistance is by applying Ohm’s law:

This necessitates, in some cases, finding the total current first. The following example should make this clear.

EXAMPLE 11–1

Given: The circuit shown in Figure 11–3.

Find:

With the number 0.3667 in your calculator display, press 1/X again and obtain the answer: 2.73. The series of keys to press on a scientific calculator to determine the correct answer is shown in Figure 11–5.

Method #3: A Practical Method

The reciprocal equation inevitably requires the finding of the lowest common denominator. This procedure could, at times, be cumbersome. The following method is offered as an alternative practical solution. This method works in all cases.

EXAMPLE 11–3

Given: The circuit shown in Figure 11–6.

Find: The total resistance.

Solution

Pick the largest resistance value in the circuit; then divide it by all the parallel resistors (including itself).

Now that you have been given an example, try to do it yourself. Substitute the numbers 20, 30, and 60 for the resistance values shown in Figure 11–6. When you are done, you should get 10 ohms for an answer. If not, better try again.

Method #4: The Product Over the Sum Formula

This is a quick way of getting the answer, provided that only two resistors are given. Study the example shown here. The equation to be used is

EXAMPLE 11–4

Given: The circuit shown in Figure 11–7.

Find: The total circuit resistance.

Solve the above problem once again, substituting 15 ohms for R1 and 30 ohms for R2. Your answer should be 10 ohms.

Method #5: A Special Condition: All Equal Resistors

Occasionally, you may encounter circuits where all load resistors are of identical value. That makes our computation really easy. We merely take the resistance value of one device and divide it by the number of branch resistors. Mathematically, we might state it like this:

What answers did you get for the circuits shown in D and E? Do you agree with 12 and 10 ohms, respectively?

As with series circuits, there are three rules, when used with Ohm’s law, that can be applied in solving for unknown electrical quantities in parallel circuits.

1. Voltage is the same across all branches of a parallel circuit. (Voltage remains the same.)

2. The total current is the sum of the currents through individual branches. (Current adds.)

3. The reciprocal of the total resistance is equal to the sum of the reciprocals of the resistance of each branch.

11–3 POWER DISSIPATION IN PARALLEL CIRCUITS

Each resistor develops heat in accordance with the amount of current flowing through it. Regardless of the type of circuit involved, the power dissipated by R1 is P1 5 E1I1. Likewise, P2 5 E2I2; P3 5 E3I3, and so on.

The total circuit power (PT) is simply the sum of all the various power dissipations on the branch resistors. Mathematically stated,

PT 5 P1 1 P2 1 P3 1 . . . 1 Pn

Of course, if the total current is known, it is even simpler to compute PT directly by using the power equation PT 5 ET IT or PT 5 (IT)2 RT.

EXAMPLE 11–6

Given: The circuit shown in Figure 11–9.

Find: The total power consumption.

Parallel Circuits

11–1 THE NATURE OF PARALLEL CIRCUITS

You should recall that series circuits were defined as having one, and only one, path along which the current can flow. By contrast, a parallel circuit has more than one path through which the current can flow. Figure 11–1 is such a parallel circuit. This is the standard representation where all resistors are drawn parallel to one another, resembling the ties between railroad tracks.

Now look at the two schematics in Figure 11–2, which are representations of the same parallel circuit shown in Figure 11–1. The common feature of these parallel circuits can be detected by carefully tracing each possible current path. Then it will become clear that each individual resistor is connected to the negative and positive pole of the battery. If you have difficulty in perceiving this fact, trace the negative and positive supply lines with two different-colored pencils from the source to each resistor.

What all these drawings convey is the fact that there is only one voltage serving all load resistors. (Compare this with the characteristics of a series circuit, where every resistor may have a different voltage drop.) Mathematically stated,

Also, as you trace the current path from its power source, you will notice that the current divides at some junction point, flows through the individual branch resistors, and then recombines at some other junction point before it returns to the power source.

Now, carefully check the three drawings just mentioned. They all show identical current flow to demonstrate that the total line current (supplied by the source) is equal to the sum of all the individual branch currents. (Compare this with the characteristics of a series circuit, where we dealt with one common current in each part of the circuit.) Mathematically stated,

We have compared the voltage and current distribution of parallel circuits with that of series circuits. Now it is time to compare the total resistance of such circuits.

In a series circuit, as you should recall, the total resistance increases with every additional resistance. In parallel circuits, by contrast, we encounter exactly the opposite.

In other words, the total resistance of a parallel circuit decreases whenever additional resistors are connected to the circuit. In fact, the total resistance is always smaller than any of the individual branch resistors.

There are five different methods by which the total resistance of a parallel circuit may be computed. How to employ these methods will be the subject of the next few sections.

11–2 FIVE METHODS OF COMPUTATION

Method #1: Use of Ohm’s Law for Computing RT

An easy way of determining the total resistance is by applying Ohm’s law:

This necessitates, in some cases, finding the total current first. The following example should make this clear.

EXAMPLE 11–1

Given: The circuit shown in Figure 11–3.

Find:

With the number 0.3667 in your calculator display, press 1/X again and obtain the answer: 2.73. The series of keys to press on a scientific calculator to determine the correct answer is shown in Figure 11–5.

Method #3: A Practical Method

The reciprocal equation inevitably requires the finding of the lowest common denominator. This procedure could, at times, be cumbersome. The following method is offered as an alternative practical solution. This method works in all cases.

EXAMPLE 11–3

Given: The circuit shown in Figure 11–6.

Find: The total resistance.

Solution

Pick the largest resistance value in the circuit; then divide it by all the parallel resistors (including itself).

Now that you have been given an example, try to do it yourself. Substitute the numbers 20, 30, and 60 for the resistance values shown in Figure 11–6. When you are done, you should get 10 ohms for an answer. If not, better try again.

Method #4: The Product Over the Sum Formula

This is a quick way of getting the answer, provided that only two resistors are given. Study the example shown here. The equation to be used is

EXAMPLE 11–4

Given: The circuit shown in Figure 11–7.

Find: The total circuit resistance.

Solve the above problem once again, substituting 15 ohms for R1 and 30 ohms for R2. Your answer should be 10 ohms.

Method #5: A Special Condition: All Equal Resistors

Occasionally, you may encounter circuits where all load resistors are of identical value. That makes our computation really easy. We merely take the resistance value of one device and divide it by the number of branch resistors. Mathematically, we might state it like this:

What answers did you get for the circuits shown in D and E? Do you agree with 12 and 10 ohms, respectively?

As with series circuits, there are three rules, when used with Ohm’s law, that can be applied in solving for unknown electrical quantities in parallel circuits.

1. Voltage is the same across all branches of a parallel circuit. (Voltage remains the same.)

2. The total current is the sum of the currents through individual branches. (Current adds.)

3. The reciprocal of the total resistance is equal to the sum of the reciprocals of the resistance of each branch.

11–3 POWER DISSIPATION IN PARALLEL CIRCUITS

Each resistor develops heat in accordance with the amount of current flowing through it. Regardless of the type of circuit involved, the power dissipated by R1 is P1 5 E1I1. Likewise, P2 5 E2I2; P3 5 E3I3, and so on.

The total circuit power (PT) is simply the sum of all the various power dissipations on the branch resistors. Mathematically stated,

PT 5 P1 1 P2 1 P3 1 . . . 1 Pn

Of course, if the total current is known, it is even simpler to compute PT directly by using the power equation PT 5 ET IT or PT 5 (IT)2 RT.

EXAMPLE 11–6

Given: The circuit shown in Figure 11–9.

Find: The total power consumption.

10–6 VOLTAGE DROP ON A LINE

Why do the lights in a house dim when a motor starts? The question is answered by Ohm’s law and the use of the series circuit principle.

The sum of individual voltages equals the total applied voltage.

Assume that each wire leading to the house, as illustrated in Figure 10–10A, has 0.5-ohm resistance and that lamps in the house cause a 2-ampere current in the line. We then have a series circuit and can calculate the voltage at the house.

Each line wire is, in effect, a 0.5-ohm resistor with 2 amperes through it.

which is the potential energy used to maintain the 2-ampere current in the 0.5-ohm resistance of the wire. One volt is used on each wire, since the potential difference between the wires at the house is equal to 120 2 2 or 118 volts, as shown in Figure 10–10B.

If a motor is turned on so that the current in the line becomes 20 amperes instead of 2 amperes, more voltage will be required to maintain the current in the line leading to the house.

E = IR

E = 20 x 0.5

E = 10 V for each wire

Therefore, subtracting 20 volts from 120 volts gives 100 volts delivered at the house, as shown in Figure 10–10C.

With 2 amperes in the line, the voltage at the house is 118 volts; and with 20 amperes in the line, the voltage at the house is 100 volts. Lighting in the house is dimmer on 100 volts than on 118 volts, since the decreased voltage means that there is less current in the lamps. This 2-volt or 20-volt loss is called the voltage drop on the line. According to Ohm’s law, this voltage depends on the resistance of the line and the current in the line (ED = IL x RL).

EXAMPLE 10–7

Given: A certain electric motor requires at least 12 amperes at 110 volts to operate properly, as shown in Figure 10–11, and the motor is to be used 500 feet from a 120-volt power line.

Find: The size copper wire needed for the 500-foot extension.

Solution

Since the source is 120 volts and 110 volts must be delivered to the motor, the difference, 10 volts, can be used by the wire when the current is 12 amperes. Since E and I are known, we can find the resistance of the extension wires.

R =E/I

R = 0.83 Ω

(These wires are a resistance in series with the motor. Applying Ohm’s law, we used the 10 volts to find the resistance of the wire that is responsible for the 10-volt potential difference.)

The wire size can now be found from tables. (See Figure A–2 in the Appendix: American Wire Gauge.) The 500-foot extension requires 1,000 feet of wire with no

more than 0.83 ohms of resistance. Using the “Ohms per 1,000 ft.” column in Figure A–2, we find that the closest wire size is #9. (If #9 copper wire were not available, then the extension could be made of #8 copper wire.)

10–7 VOLTAGE AT AN OPEN ELEMENT

In Figure 10–12 there were seven lamps in the series circuit, but one lamp has been removed. How much voltage, if any, exists across the open socket?

One way of arriving at the answer is to consider how much of the 220-volt source is being used on each of the six remaining lamps, using E 5 IR. The current in each lamp is zero. As a result, each lamp has 0 volts across it; therefore, the entire 220-volt potential appears at the open socket.

The same reasoning applies to voltage at an open switch. The pressure is there, even though it may not be causing any current.

10–8 SERIES CIRCUITS AS VOLTAGE DIVIDERS

When series circuits are used for the purpose of obtaining different voltages from one voltage source, they are known as voltage dividers. The principle of voltage division was implied earlier, in Section 10–3, where it was stated that “. . . voltage drops are proportional to the values of the resistors.” In other words, voltage dividers are series circuits in which the source voltage is divided among the resistors proportionally to their ohmic values.

The six circuit diagrams shown in Figure 10–13 will help clarify this point, especially if you make the effort to confirm the mathematical accuracy by using Ohm’s law.

In some applications, voltage division is achieved by means of potentiometers. You may wish to refresh your memory on that subject by rereading Section 7–12, dealing with variable resistors.

Remember, a potentiometer is a three-terminal device having the same effect as the two-resistor circuit in Figure 10–13A. In fact, the movable contact of the potentiometer divides the resistance element into two series-connected resistors. By varying the setting of the movable contact, any voltage drop from zero to maximum can be obtained, as shown in Figure 10–14.

10-9 THE GENERAL VOLTAGE DIVIDER FORMULA

A common method for determining the voltage drop across series elements is to use the general voltage divider formula. Since the current flow through a series circuit is the same at all points in the circuit, the voltage drop across any particular resistance is equal to the total circuit current times the value of that resistor:

The voltage drop across any series component (EX) can be determined by substituting the value of RX for the resistance value of any component when the source voltage and total resistance are known.

EXAMPLE 10–8

A series circuit containing three resistors is connected to a 48-volt source. Resistor R1 has a value of 400 ohms, R2 a value of 600 ohms, and R3 a value of 280 ohms. What is the voltage drop across each resistor?

Solution

Find the total resistance of the circuit.

10–10 POLARITY CONSIDERATIONS

In discussing the voltage distribution of a circuit, it is not good enough to merely refer to the magnitude of the voltages. Equal consideration should be given to the polarity of the voltages.

To illustrate this point, let us have another look at a voltage divider circuit in which we have identified the terminal points of the resistors with letters, as shown in Figure 10–15.

To determine the polarity of a voltage drop, we simply consider the direction of the current. Remember, electrons move from negative to positive, as indicated by the arrows in our drawing. Since the electrons flow from point A toward point B, it follows that point A is negative with respect to point B. (We could have said, instead, that point B is positive with respect to point A.) Similarly, point B is negative with respect to point C (or point C is positive with respect to point B).

Do not be confused by the two polarity markings (1 and 2) at points B, C, and D. Some students may wonder how any given point can be assigned both positive and negative

markings at the same time. This simply depends on your reference point. Point C is positive with respect to point B, but it is negative with respect to point D. This is somewhat analogous to describing someone’s age. A person can be described as being young and old at the same time. Compared to your grandfather, you are young; but compared to your baby brother, you are old.

10–11 GROUND AS A REFERENCE POINT

The concept of a reference point is important in describing not only polarity markings but voltage levels as well. In electrical theory such reference points are often called ground, regardless of whether or not they are actually connected to the earth. Automobiles, for instance, are said to have a negative ground. That simply means that the chassis, connected to the negative terminal of the battery, is the common reference point. But certainly the car is not grounded to the earth. If anything, it is well insulated from the earth by its rubber tires.

Two graphic symbols are used in schematics to denote a ground, as shown in Figure 10–16. The first, Figure 10–16A, is used to describe a chassis ground. Let us employ that symbol to denote a reference point in the voltage divider circuit of Figure 10–15.

We are going to place this reference point first on point A, then on point B, then on to points C, D, and E. The schematics shown in Figure 10–17 will show how the voltage levels on each point change with every change of the reference ground.

Be sure to study these drawings to gain understanding of this important principle. The same concept will be presented in the following section, as well as in Chapter 12.

10–12 VOLTAGE SOURCES IN SERIES

Cells and other voltage sources are often connected in series to obtain higher volt- ages. The voltage produced by several cells connected in series is the total of the individual cell voltages; see Figure 10–18. This method of connecting voltage sources is known as series-aiding. Note that with this method, the positive pole of one source always connects with the negative pole of another source. A familiar example of this is the loading of a flashlight with multiple dry cells.

Consider, by contrast, two voltage sources interconnected with identical poles, as shown in Figure 10–19. Such connections are known as series-opposing. When voltage sources are connected like this, their voltages subtract from one another. If the individual source voltages are equal, their combined output will equal 0 volts, as shown in Figure 10–19A.

If the individual source voltages are of different magnitude, their net difference will represent the output voltage, with the larger of the two determining the polarity of the output. (Compare Figures 10–19B and C.)

SUMMARY

• In series circuits there is only one path for the current.

• In series circuits the current is the same for all components.

• In series circuits the sum of all voltage drops is equal to the applied voltage.

• In series circuits the total circuit resistance is equal to the sum of all the individual resistors.

• In series circuits the total circuit power is equal to the sum of all the individual resistors’ power dissipation.

• Long power lines supplying a load represent resistors in series with the load causing a voltage drop in the line.

• When one resistor element in a series circuit opens up, the source voltage will appear

across its terminals.

• Series circuits may be considered voltage dividers.

• Voltage division is achieved proportionally to the values of the resistors.

• The general voltage divider formula is used to determine the voltage drop across series elements

• The polarity of voltage drops is negative at the point where the electron current enters the resistor and positive where the current exits.

• The word ground denotes a common reference point.

• Voltage sources may be connected series-aiding or series-opposing.

Achievement Review

Note: For each problem, draw a circuit diagram to gain practice in schematic work and to aid in visualizing each problem. All answers must include units of measurement.

1. In a television receiver, two resistors are in series. The first resistor (R1) has a voltage drop of 200 volts across it. The second resistor (R2) has a drop of 50 volts across it. Current in the circuit is 20 milliamperes (0.02 A). What is the value of each resistor? What is the total resistance?

2. In question 1, what wattage is dissipated by each resistor?

3. Across a 300-volt power supply in an electronic device there are four resistors in series. Resistor values are 20,000, 50,000, 500, and 4,500 ohms. What is the current, in milliamperes, that flows through this network?

4. In a radio there are three resistors in series: R1 has a 1.5-volt drop across it; R2 has a 3-volt drop across it; and R3 has a 0.6-volt drop across it. R3 is 20 ohms. What is the current in the circuit, and what are the resistance values of R1 and R2?

5. Consider a barn located a considerable distance from a farmhouse. The two wires supplying the power to the barn have a resistance of 0.3 ohm each. The resistance of these wires forms a series circuit with the load (machinery) in the barn. The voltage at the farmhouse is 120 volts. How many volts will be avail- able at the barn when 20 amperes is supplied?

6. Explain how the answer would change in question 5 if the current were increased to 35 amperes. Specifically, what effect would this have on the machinery to be operated in the barn?

7. Two resistors are connected in series across a 24-volt power supply. A voltage drop of 9 volts can be measured across the first resistor. The current through the second resistor is 1.5 amperes. What are the values of the two resistors?

8. Vacuum tubes such as the ones used in older radios or TVs require different volt- ages for their heaters. An efficient method of connecting such heaters is in a series configuration, providing that all tubes require the same heater current. Consider the following four tubes connected in such a manner to a 120-volt supply:

Tube #1 requires 25 V/0.3 A

Tube #2 requires 12 V/0.3 A

Tube #3 requires 6 V/0.3 A

Tube #4 requires 12 V/0.3 A

If the tubes were to be connected to a 120-volt circuit, an additional series-drop- ping resistor would be needed to compensate for the difference in voltages. What must be the ohms and wattage rating of such a resistor?

9. A motor rated for use on a 230-volt line can generally tolerate 7% voltage fluctuation.

a. What is the lowest voltage it will tolerate?

b. Assuming that such a motor will draw 12 amperes when run at 214 volts, if the motor is located 800 feet away from the power source, what size wire must be installed? Let us find out! First, draw a simple schematic diagram like this.

Note that the resistances of the wires are connected in series with the motor, dropping a voltage along the way that is lost to the motor.

c. How much is the voltage drop in the wire?

d. Using this answer (and Ohm’s law) find the maximum resistance permissible

in the wire.

e. How many feet of wire are needed for this installation?

f. Use the preceding two answers to compute the number of ohms per 1,000 feet.

g. Now consult your wire table to find the proper wire size for this installation.

10. An advertising sign is to be constructed with low-voltage lightbulbs rated at 6 V/25 W. The bulbs will be connected to a source of 114 volts.

a. How many lamps should be used?

b. If only 16 bulbs were used, how much voltage would each lamp receive?

c. What effect will this have on the current?

d. How will this affect the life span of the bulb?

By contrast, if 20 or more lamps were to be used, what effect would this have on

e. The light intensity?

f. The power consumption?

11. Find E_T and P₂.

10–6 VOLTAGE DROP ON A LINE

Why do the lights in a house dim when a motor starts? The question is answered by Ohm’s law and the use of the series circuit principle.

The sum of individual voltages equals the total applied voltage.

Assume that each wire leading to the house, as illustrated in Figure 10–10A, has 0.5-ohm resistance and that lamps in the house cause a 2-ampere current in the line. We then have a series circuit and can calculate the voltage at the house.

Each line wire is, in effect, a 0.5-ohm resistor with 2 amperes through it.

which is the potential energy used to maintain the 2-ampere current in the 0.5-ohm resistance of the wire. One volt is used on each wire, since the potential difference between the wires at the house is equal to 120 2 2 or 118 volts, as shown in Figure 10–10B.

If a motor is turned on so that the current in the line becomes 20 amperes instead of 2 amperes, more voltage will be required to maintain the current in the line leading to the house.

E = IR

E = 20 x 0.5

E = 10 V for each wire

Therefore, subtracting 20 volts from 120 volts gives 100 volts delivered at the house, as shown in Figure 10–10C.

With 2 amperes in the line, the voltage at the house is 118 volts; and with 20 amperes in the line, the voltage at the house is 100 volts. Lighting in the house is dimmer on 100 volts than on 118 volts, since the decreased voltage means that there is less current in the lamps. This 2-volt or 20-volt loss is called the voltage drop on the line. According to Ohm’s law, this voltage depends on the resistance of the line and the current in the line (ED = IL x RL).

EXAMPLE 10–7

Given: A certain electric motor requires at least 12 amperes at 110 volts to operate properly, as shown in Figure 10–11, and the motor is to be used 500 feet from a 120-volt power line.

Find: The size copper wire needed for the 500-foot extension.

Solution

Since the source is 120 volts and 110 volts must be delivered to the motor, the difference, 10 volts, can be used by the wire when the current is 12 amperes. Since E and I are known, we can find the resistance of the extension wires.

R =E/I

R = 0.83 Ω

(These wires are a resistance in series with the motor. Applying Ohm’s law, we used the 10 volts to find the resistance of the wire that is responsible for the 10-volt potential difference.)

The wire size can now be found from tables. (See Figure A–2 in the Appendix: American Wire Gauge.) The 500-foot extension requires 1,000 feet of wire with no

more than 0.83 ohms of resistance. Using the “Ohms per 1,000 ft.” column in Figure A–2, we find that the closest wire size is #9. (If #9 copper wire were not available, then the extension could be made of #8 copper wire.)

10–7 VOLTAGE AT AN OPEN ELEMENT

In Figure 10–12 there were seven lamps in the series circuit, but one lamp has been removed. How much voltage, if any, exists across the open socket?

One way of arriving at the answer is to consider how much of the 220-volt source is being used on each of the six remaining lamps, using E 5 IR. The current in each lamp is zero. As a result, each lamp has 0 volts across it; therefore, the entire 220-volt potential appears at the open socket.

The same reasoning applies to voltage at an open switch. The pressure is there, even though it may not be causing any current.

10–8 SERIES CIRCUITS AS VOLTAGE DIVIDERS

When series circuits are used for the purpose of obtaining different voltages from one voltage source, they are known as voltage dividers. The principle of voltage division was implied earlier, in Section 10–3, where it was stated that “. . . voltage drops are proportional to the values of the resistors.” In other words, voltage dividers are series circuits in which the source voltage is divided among the resistors proportionally to their ohmic values.

The six circuit diagrams shown in Figure 10–13 will help clarify this point, especially if you make the effort to confirm the mathematical accuracy by using Ohm’s law.

In some applications, voltage division is achieved by means of potentiometers. You may wish to refresh your memory on that subject by rereading Section 7–12, dealing with variable resistors.

Remember, a potentiometer is a three-terminal device having the same effect as the two-resistor circuit in Figure 10–13A. In fact, the movable contact of the potentiometer divides the resistance element into two series-connected resistors. By varying the setting of the movable contact, any voltage drop from zero to maximum can be obtained, as shown in Figure 10–14.

10-9 THE GENERAL VOLTAGE DIVIDER FORMULA

A common method for determining the voltage drop across series elements is to use the general voltage divider formula. Since the current flow through a series circuit is the same at all points in the circuit, the voltage drop across any particular resistance is equal to the total circuit current times the value of that resistor:

The voltage drop across any series component (EX) can be determined by substituting the value of RX for the resistance value of any component when the source voltage and total resistance are known.

EXAMPLE 10–8

A series circuit containing three resistors is connected to a 48-volt source. Resistor R1 has a value of 400 ohms, R2 a value of 600 ohms, and R3 a value of 280 ohms. What is the voltage drop across each resistor?

Solution

Find the total resistance of the circuit.

10–10 POLARITY CONSIDERATIONS

In discussing the voltage distribution of a circuit, it is not good enough to merely refer to the magnitude of the voltages. Equal consideration should be given to the polarity of the voltages.

To illustrate this point, let us have another look at a voltage divider circuit in which we have identified the terminal points of the resistors with letters, as shown in Figure 10–15.

To determine the polarity of a voltage drop, we simply consider the direction of the current. Remember, electrons move from negative to positive, as indicated by the arrows in our drawing. Since the electrons flow from point A toward point B, it follows that point A is negative with respect to point B. (We could have said, instead, that point B is positive with respect to point A.) Similarly, point B is negative with respect to point C (or point C is positive with respect to point B).

Do not be confused by the two polarity markings (1 and 2) at points B, C, and D. Some students may wonder how any given point can be assigned both positive and negative

markings at the same time. This simply depends on your reference point. Point C is positive with respect to point B, but it is negative with respect to point D. This is somewhat analogous to describing someone’s age. A person can be described as being young and old at the same time. Compared to your grandfather, you are young; but compared to your baby brother, you are old.

10–11 GROUND AS A REFERENCE POINT

The concept of a reference point is important in describing not only polarity markings but voltage levels as well. In electrical theory such reference points are often called ground, regardless of whether or not they are actually connected to the earth. Automobiles, for instance, are said to have a negative ground. That simply means that the chassis, connected to the negative terminal of the battery, is the common reference point. But certainly the car is not grounded to the earth. If anything, it is well insulated from the earth by its rubber tires.

Two graphic symbols are used in schematics to denote a ground, as shown in Figure 10–16. The first, Figure 10–16A, is used to describe a chassis ground. Let us employ that symbol to denote a reference point in the voltage divider circuit of Figure 10–15.

We are going to place this reference point first on point A, then on point B, then on to points C, D, and E. The schematics shown in Figure 10–17 will show how the voltage levels on each point change with every change of the reference ground.

Be sure to study these drawings to gain understanding of this important principle. The same concept will be presented in the following section, as well as in Chapter 12.

10–12 VOLTAGE SOURCES IN SERIES

Cells and other voltage sources are often connected in series to obtain higher volt- ages. The voltage produced by several cells connected in series is the total of the individual cell voltages; see Figure 10–18. This method of connecting voltage sources is known as series-aiding. Note that with this method, the positive pole of one source always connects with the negative pole of another source. A familiar example of this is the loading of a flashlight with multiple dry cells.

Consider, by contrast, two voltage sources interconnected with identical poles, as shown in Figure 10–19. Such connections are known as series-opposing. When voltage sources are connected like this, their voltages subtract from one another. If the individual source voltages are equal, their combined output will equal 0 volts, as shown in Figure 10–19A.

If the individual source voltages are of different magnitude, their net difference will represent the output voltage, with the larger of the two determining the polarity of the output. (Compare Figures 10–19B and C.)

SUMMARY

• In series circuits there is only one path for the current.

• In series circuits the current is the same for all components.

• In series circuits the sum of all voltage drops is equal to the applied voltage.

• In series circuits the total circuit resistance is equal to the sum of all the individual resistors.

• In series circuits the total circuit power is equal to the sum of all the individual resistors’ power dissipation.

• Long power lines supplying a load represent resistors in series with the load causing a voltage drop in the line.

• When one resistor element in a series circuit opens up, the source voltage will appear

across its terminals.

• Series circuits may be considered voltage dividers.

• Voltage division is achieved proportionally to the values of the resistors.

• The general voltage divider formula is used to determine the voltage drop across series elements

• The polarity of voltage drops is negative at the point where the electron current enters the resistor and positive where the current exits.

• The word ground denotes a common reference point.

• Voltage sources may be connected series-aiding or series-opposing.

Achievement Review

Note: For each problem, draw a circuit diagram to gain practice in schematic work and to aid in visualizing each problem. All answers must include units of measurement.

1. In a television receiver, two resistors are in series. The first resistor (R1) has a voltage drop of 200 volts across it. The second resistor (R2) has a drop of 50 volts across it. Current in the circuit is 20 milliamperes (0.02 A). What is the value of each resistor? What is the total resistance?

2. In question 1, what wattage is dissipated by each resistor?

3. Across a 300-volt power supply in an electronic device there are four resistors in series. Resistor values are 20,000, 50,000, 500, and 4,500 ohms. What is the current, in milliamperes, that flows through this network?

4. In a radio there are three resistors in series: R1 has a 1.5-volt drop across it; R2 has a 3-volt drop across it; and R3 has a 0.6-volt drop across it. R3 is 20 ohms. What is the current in the circuit, and what are the resistance values of R1 and R2?

5. Consider a barn located a considerable distance from a farmhouse. The two wires supplying the power to the barn have a resistance of 0.3 ohm each. The resistance of these wires forms a series circuit with the load (machinery) in the barn. The voltage at the farmhouse is 120 volts. How many volts will be avail- able at the barn when 20 amperes is supplied?

6. Explain how the answer would change in question 5 if the current were increased to 35 amperes. Specifically, what effect would this have on the machinery to be operated in the barn?

7. Two resistors are connected in series across a 24-volt power supply. A voltage drop of 9 volts can be measured across the first resistor. The current through the second resistor is 1.5 amperes. What are the values of the two resistors?

8. Vacuum tubes such as the ones used in older radios or TVs require different volt- ages for their heaters. An efficient method of connecting such heaters is in a series configuration, providing that all tubes require the same heater current. Consider the following four tubes connected in such a manner to a 120-volt supply:

Tube #1 requires 25 V/0.3 A

Tube #2 requires 12 V/0.3 A

Tube #3 requires 6 V/0.3 A

Tube #4 requires 12 V/0.3 A

If the tubes were to be connected to a 120-volt circuit, an additional series-drop- ping resistor would be needed to compensate for the difference in voltages. What must be the ohms and wattage rating of such a resistor?

9. A motor rated for use on a 230-volt line can generally tolerate 7% voltage fluctuation.

a. What is the lowest voltage it will tolerate?

b. Assuming that such a motor will draw 12 amperes when run at 214 volts, if the motor is located 800 feet away from the power source, what size wire must be installed? Let us find out! First, draw a simple schematic diagram like this.

Note that the resistances of the wires are connected in series with the motor, dropping a voltage along the way that is lost to the motor.

c. How much is the voltage drop in the wire?

d. Using this answer (and Ohm’s law) find the maximum resistance permissible

in the wire.

e. How many feet of wire are needed for this installation?

f. Use the preceding two answers to compute the number of ohms per 1,000 feet.

g. Now consult your wire table to find the proper wire size for this installation.

10. An advertising sign is to be constructed with low-voltage lightbulbs rated at 6 V/25 W. The bulbs will be connected to a source of 114 volts.

a. How many lamps should be used?

b. If only 16 bulbs were used, how much voltage would each lamp receive?

c. What effect will this have on the current?

d. How will this affect the life span of the bulb?

By contrast, if 20 or more lamps were to be used, what effect would this have on

e. The light intensity?

f. The power consumption?

11. Find E_T and P₂.