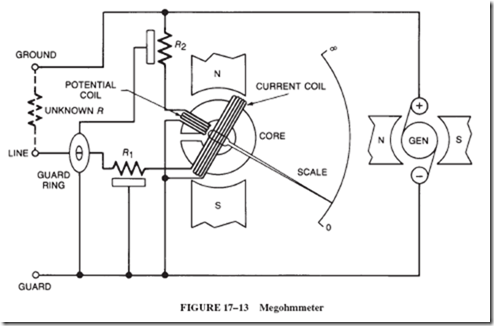
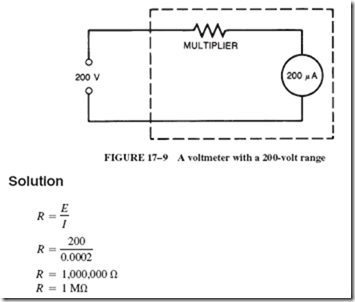
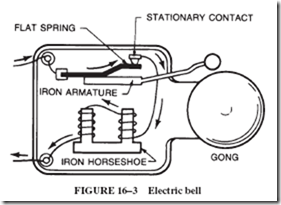
15–6 PERMANENT MAGNETS
A rough classification divides magnets into two groups: permanent or temporary. A permanent magnet will keep its strength after the magnetizing force is removed; that is, the magnet maintains its orderly atomic arrangement. Before 1920, high-carbon tool steels (cobalt, molybdenum, and chrome-tungsten) were the only useful permanent-magnet materials. These materials were and still are used in engine magnetos, telephone ringers and receivers, electrical measuring instruments, and compass needles. The discovery that weakly magnetic and nonmagnetic metals can be alloyed to make strong magnets promptly led to the commercial development of dozens of new magnetic materials that have better magnetic properties than the steel materials.
Alnico 5 is presently the most frequently used permanent magnet material. It can be found in loudspeakers, toys, and door latches. Alnico 5 is also used in magnetic separators; rotors for small generators; magnetic chucks and holding devices; and motors used in aircraft, automobiles, computers, and small appliances. Permanent magnets are replacing small electromagnets in many simple applications.
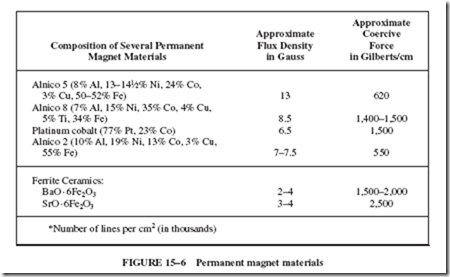
In Figure 15–6, the term coercive force refers to the difficulty of magnetizing or demagnetizing a magnet. The coercive force of permanent-magnet steels is about 200. Alnico 5 makes a stronger magnetic field than do the magnets made of the steel materials and is about three times as difficult to demagnetize.
The properties of magnetic materials depend on their composition and are influenced by the methods used to manufacture and treat the materials. Alloys can be cast from molten metal or formed by sintering. (Sintering is the high-temperature heating of a compressed fine-powder mixture.) Rolling and heat treatment cause changes in the grain structure and magnetic properties of alloys. The compounds barium ferrite and strontium ferrite are formed by sintering and are called ceramic magnets. These materials have the properties of stone rather than those of metal. Ferrites are useful in several different forms: they can be
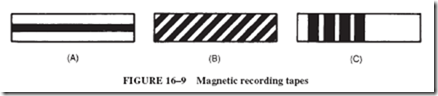
used in the bulk solid form; they can be powdered and mixed with plastic or rubber; or they can be mixed with liquid to make a product such as the magnetic printing ink used for the numbers at the bottom of bank checks. The brown material on magnetic recording tapes is a magnetic iron oxide.
The strength of a given permanent magnet is limited. When all of the atoms are facing in the same direction, the magnet achieves its maximum strength. This state is called saturation.
15–7 ELECTROMAGNETISM OF A STRAIGHT WIRE
The first experimentation leading to the conclusion that magnetism was in some way connected with electrical behavior occurred in 1819. Hans Oersted, a physics professor in Denmark, noted that a magnetic compass needle was affected by a wire that was connected to a battery.
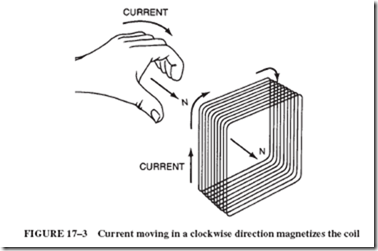
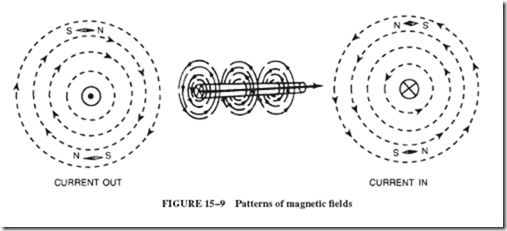
Assume that a wire connected to a battery is inserted through the black dot in the center of Figure 15–7 and is held perpendicular to the paper. The wire is connected to a battery so that electrons come from behind the page toward the reader. Compasses placed on the paper near the wire will point as shown. The north ends of the compasses point in the direction shown by the clockwise arrows around the wire.
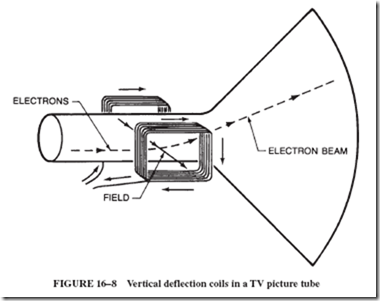
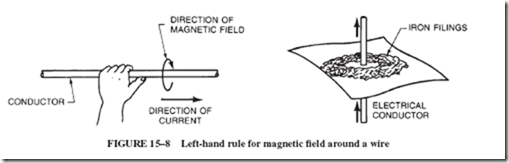
In other words, Oersted discovered that a current-carrying conductor produces a circular magnetic field about itself. The circular pattern becomes more evident when iron filings are sprinkled on a plane through which the wire is stuck, as shown in Figure 15–8.
It can be shown that the density of these circular flux lines is strongest near the wire and weakens with distance from the wire. More importantly, the direction of the circular flux depends on the direction of the current.
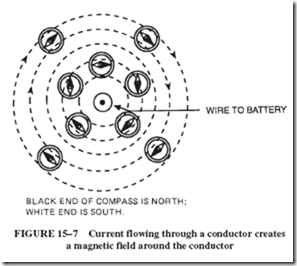
If the direction of electron flow is known, the direction of the magnetic field can be found as shown in Figure 15–8. If a wire is grasped with the left hand so that the thumb points in the direction of the electron current, the fingers will encircle the wire in the same direction as the magnetic lines of force. (The direction of the field is the direction in which the north pole of the compass is pointing.)
Conversely, if it is necessary to determine the direction of the electron current, the field direction can be found with a compass. Then, if the wire is grasped so that the fin- gers point around the wire in the direction indicated by the north pole of the compass, the thumb gives the direction of the electron flow.
The pattern of the magnetic field is shown in Figure 15–9. The dot in the center of the left-hand wire indicates that the arrow showing current direction is pointing toward the observer. The X in the right-hand wire indicates that the current arrow is pointing away from the observer.
If two current-carrying conductors are placed in close proximity to one another, a force of attraction or repulsion may be observed between the two wires.
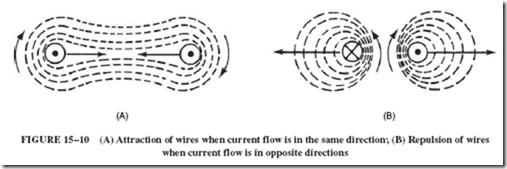
In 1822, Andre Ampére reported: “I observed that when I passed a current of electricity in both of these wires at once, they attracted each other when the two currents were in the same direction, and repelled each other when the currents were in opposite directions . . .” Figure 15–10 illustrates this principle. Figure 15–10A shows how currents flowing in the same direction cause the magnetic fields about the two wires to join and reinforce each other. Since flux lines are said to contract like stretched rubber bands, the conductors will move toward one another.
Compare this with Figure 15–10B, where currents in opposite directions cause op- posing magnetic fields. Recall from Section 15–3 that flux lines in opposite directions repel each other; thus, the two wires will be forced apart.
(A note of explanation is in order here. Many readers think that this statement is contradicted by drawings such as Figure 15–10B. They see the two arrows in the center of the drawing, both pointing upward, and then wrongly conclude that the flux lines are pointing in the same direction. Not so! The flux lines are said to be in the opposite direction because one set is clockwise and the other set is counterclockwise.)
15–8 ELECTROMAGNETISM OF A COIL
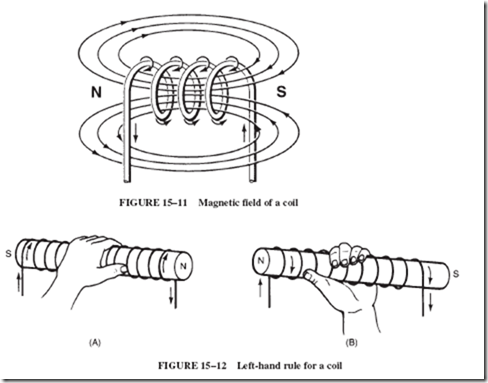
When a wire is wound into the form of a coil, as shown in Figure 15–11, each turn of wire is surrounded by its own circular magnetic field. These little whirls of magnetic force combine to produce one large field that surrounds the entire coil.
The magnetic coil shown in Figure 15–12 is termed a solenoid. The figure indicates a way of remembering the relationship between the current direction and the field direction for a coil.
The ends of the coil are, in effect, magnetic poles (whether or not there is an iron core in the coil). Therefore, if the coil is grasped with the left hand so that the fingers point in the same direction as the electron current in the wires, the thumb points toward the north end of the coil. If the current direction is unknown but the field direction of the coil is known or can be found with a compass, the current direction can be found by the use of this left-hand coil rule.
Carefully compare the two drawings presented in Figure 15–12. Can you tell why the two electromagnets show different magnetic polarity? Note that the first coil is wound in a clockwise direction. The other coil is wound counterclockwise. Consequently, the left hand must be switched around so that the fingertips line up with the current.
15–9 THE MAGNETIC CORE IN THE COIL
The illustrations of Figure 15–12 show the coils wrapped around a core. The material of such a core greatly determines the magnetizing ability of a solenoid. If the core is made of a ferromagnetic substance, the magnetomotive force (mmf) is greatly enhanced by the core’s ability to concentrate the lines of flux. The magnetomotive force (mmf) of a coil is described and measured in either of two ways.
1. The magnetizing ability of a coil, or magnetic strength, is represented by a certain number of lines of force, or flux lines, in each square inch of sectional area of the coil. The number of lines of force per square inch is called the flux density. Flux means the total number of lines of force.
2. The magnetizing ability can also be represented by the number of ampere-turns of the coil. This quantity is obtained by multiplying the current (in amperes) by the number of turns of wire in the coil. A current of 2 amperes in a coil of 20 turns provides the same magnetic effect as a current of 4 amperes in a coil of 10 turns, or 0.5 ampere in an 80-turn coil. A current of 2 amperes in a 100-turn coil has five times as much magnetizing force as 2 amperes in a 20-turn coil.
The presence of nonmagnetic materials in the DC magnet coil has no appreciable effect on its magnetic force. The insertion of magnetic material inside the coil results in a great increase in the total force. Assume that we have a long coil of wire with enough cur- rent in it to produce a magnetic field whose strength is indicated by 10 lines of force; see Figure 15–13A. When a bar of magnetic material is inserted inside the coil, the material is
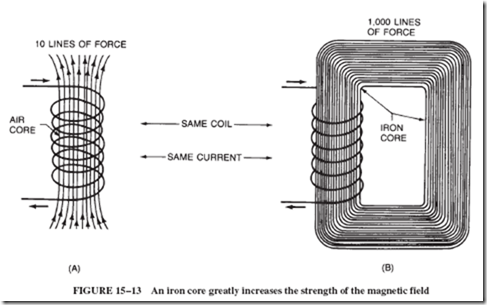
magnetized and there are now 1,000 lines of force; see Figure 15–13B. The insertion of the bar of material increases the magnetic field 100 times.
The ability of a magnetic material to increase the field strength is called permeability. In other words, permeability is the number of times that the flux density is increased by the addition of the magnetic material. The permeability of the iron core in Figure 15–13B is 100.
Magnetic flux density also increases when the current in the coil increases. The manufacturers of magnetic materials provide graphs showing this relationship for each of their products, such as shown in Figure 15–14. The expression magnetizing intensity on the graph means the ampere-turns of the coil divided by the total length of the magnetic path, in inches. (Magnetic units are more fully explained in Section 15–10.)
Note that the increase of flux density has a limit at the saturation point (point S). Beyond point S the increase of current is wasteful, because no significant increase in magnetic flux can be achieved.
Two other properties of special interest can also be indicated on a graph of this type. The dashed line shows the magnetic behavior of the material as the current in the magnetizing coil is reduced. The height of point R above 0 represents residual magnetism. This is the amount of magnetism remaining in the core after the magnetizing force (the current in the coil) is removed. In good temporary magnets, residual magnetism is very low.
The relative strength of permanent magnet materials, as shown in Figure 15–6, is given in thousands of lines per square centimeter. For example, Alnico 8 has a residual magnetism of 8,500 lines per square centimeter (or 55,000 lines per square inch).
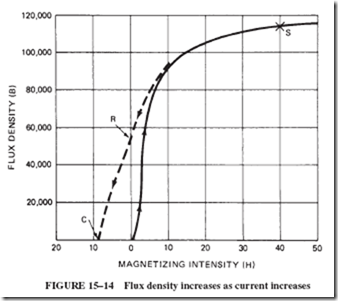
Returning to Figure 15–14, the distance on the horizontal scale from 0 to point C is a measure of coercive force. The measurement to the left on the scale indicates the amount of current in the reverse direction that must be put through the coil to remove the residual magnetism (to reduce the magnetism in the core to the zero level). If the coercive force is large, the magnet is difficult to demagnetize. A large coercive force is a desirable property for permanent magnets. However, the best materials for temporary magnets have a coercive force that is very close to zero.
The relationship between B and H, shown in the graph of Figure 15–14, can be expanded to explain a magnetic phenomenon known as hysteresis.
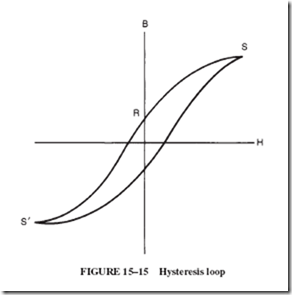
Let us assume that the current of the coil has been reduced from its point of saturation (point S in Figure 15–14) to its point of residual magnetism (point R) when the current is equal to 0 amperes. A subsequent reversal of current will not only remove the residual magnetism but also reverse the magnetic field to saturation in its opposite direction, point S9 in Figure 15–15.
The graph shown in Figure 15–15 illustrates the kind of loop generated when alternating current (AC) is applied to the coil. This is known as a hysteresis loop. The size of its area under the curve is directly related to the energy losses suffered by the coil. Such losses, given off in the form of heat, are the consequence of the molecular friction caused by the continuous reversal of the magnetic domains under the influence of alternating current.
Solenoids are temporary magnets; therefore, solenoids require core materials that readily lose their magnetism when the current to the coil is removed. In a soft alloy such as silicon-iron (2% to 4% Si), the atoms slide and rotate easily, making the magnetic organization and disorganization of atoms very easy. Silicon-iron is widely used in the production of transformers, motors, generators, relays, and in other equipment.
Many alloys that are easier to magnetize and demagnetize than iron or silicon-iron have been developed. Some of the more useful are:
Permalloy (78% nickel, 21% iron)
4–79 Permalloy (4% molybdenum, 79% nickel, 17% iron)
Mu-metal (75% nickel, 2% chromium, 5% copper, 18% iron)
Supermalloy (79% nickel, 5% molybdenum, 15% iron)
1040 Alloy (72% nickel, 14% copper, 3% molybdenum, 11% iron)
The specialized field of powder metallurgy (the process of forming alloys by mixing powdered metals and subjecting them to high pressure) produces many alloys that are useful for both temporary and permanent magnets. One alloy produced by the process of powder metallurgy, supermendur (2% vanadium, 49% iron, 49% cobalt), has the lowest coercive force of all the iron-cobalt alloys.
When iron oxide is mixed with oxides of manganese, cobalt, nickel, copper, or zinc and then is pressed and fired, the resulting temporary magnetic materials are called ferrites. These materials have good magnetic properties and high electrical resistance and thus are preferred for use in electronic equipment.
15–10 MAGNETIC QUANTITIES
A discussion of magnetic units can be somewhat confusing because three different systems of measurement have been commonly used in the analysis of magnetic circuits. Besides the English measuring system, we have to consider the metric system with two different measuring standards: the mks and the cgs system. These abbreviations simply refer to the basic units of length, mass, and time, where m stands for meter, c stands for centimeter (0.01 m), g stands for gram, k is for kilogram (1,000 grams), and s stands for time in seconds.
This fact is merely mentioned in passing so that you may appreciate the reason for the different names, symbols, and units of measurement. However, our purpose in this text is to convey the important concepts of magnetism without emphasizing the units and formulas necessary for a mathematical analysis of magnetic circuits.
Magnetic Flux
One line of magnetic flux is generally called a maxwell. One hundred million (108) lines of flux are called a weber (wb). The Greek letter f (phi) denotes magnetic flux.
Flux Density
As previously mentioned, the number of flux lines per unit area is called the flux density, denoted by the letter B. This relationship is mathematically stated by the formula
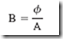
The flux density is expressed either in teslas, gausses, or lines per square inch.
tesla = webers per m2 (mks)
gauss = maxwells per cm2 (cgs)
Magnetomotive Force (mmf)
The term mmf was explained in Section 15–9 as being equivalent to the product of the current (in amperes) and the number of turns.
mmf = ampere-turns (A-turns) in both the mks and the English systems mmf is measured in gilberts (in the cgs system) 1 gilbert 5 1.26 ampere-turns Note: In addition to the number of ampere-turns, the flux density depends on the de- sign of the core—for example, its length, cross-sectional area, and type of material (permeability).
Magnetic Intensity (H)
Magnetic intensity is defined as mmf per unit length (l). In other words, a given number of ampere-turns is more intense on a short core than on a long core. The letter H denotes the magnetizing intensity. The basic mathematical statement is
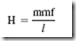
Magnetizing intensity can be expressed in ampere-turns per meter (mks system), ampere-turns per inch (English system), or gilberts per centimeter (cgs system). In the cgs system,

Note: Gilberts per centimeter are called oersteds.
Permeability (μ)
The word permeability, as mentioned earlier, refers to the ability of a substance to conduct and concentrate lines of magnetic flux. In this respect, permeability, denoted by the Greek letter μ (mu), is to magnetism what the word conductivity is to electricity.
Permeability is a pure number (without units) indicating how much better a material can establish magnetic flux within itself as compared to the permeability of a vacuum (or air).
For practical purposes, the permeability of nonmagnetic materials, such as wood, aluminum, and plastic, is the same as the permeability of a vacuum (or air). (By contrast, the ferromagnetic substances and alloys have permeability numbers ranging in the thousands.)
But, strictly speaking, even some of those nonmagnetic substances can become slightly magnetized under the influence of strong magnetic fields. Such substances are classified as being either paramagnetic or diamagnetic.
Paramagnetic substances have permeability ratings slightly greater than that of air. Aluminum is an example of a paramagnetic substance.
Diamagnetic substances have a permeability rating slightly less than that of air. Diamagnetic materials are characterized by the fact that their magnetization is in opposite direction to that of the external, magnetizing force. Copper is an example.
Reluctance
Reluctance is to magnetism what resistance is to electricity. In other words, reluctance opposes the passage of flux lines.
Recall that the resistance of a conductor can be computed by the equation
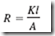
Compare this expression with a similar equation for magnetic circuits, in which reluctance is expressed as:
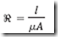
This means that, like resistance, reluctance varies directly with length and inversely with the cross-sectional area. The unit of reluctance is the rel (English) or the ampere-turn per weber (mks).
Ohm’s Law for Magnetic Circuits
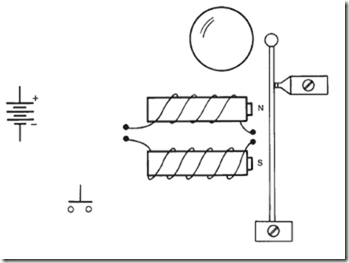
The similarities of electric circuits to magnetic circuits have been demonstrated. Com- paring the two circuits in Figure 15–16, we acknowledge that each circuit has a force (emf and mmf) between two distinctly different poles (+ and –, as well as N and S). This force must overcome a unit of opposition (resistance or reluctance) to set up a closed path for cur- rent (or flux) with a specific direction (negative to positive or north to south). Thus, it is possible to write an Ohm’s law equation for each circuit as shown in the drawing.

The term magnetic circuit can be used to mean the path of the lines of force through a magnetic device, even though there is no motion along these lines. All magnetic devices have a magnetic circuit. Beginning at any point, the magnetic circuit can be traced by following the lines of force through the iron and the air and returning to the starting point.
Recall that it is easy to magnetize iron and difficult to produce lines of force in air; therefore, the path of the lines (magnetic circuit) through air or other nonmagnetic material in all magnetic devices should be as short as possible. Figure 15–17 shows two possible
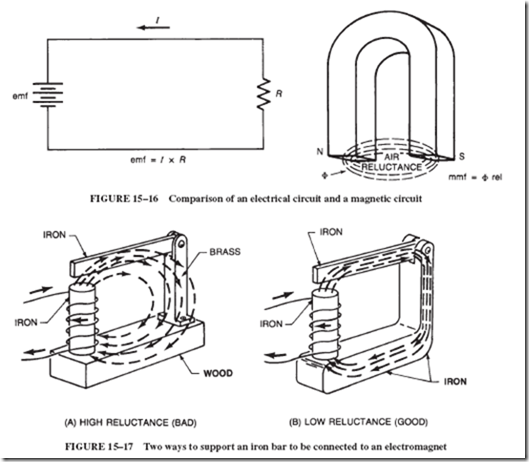
ways of supporting a pivoted iron bar so that it can be attracted to an electromagnet. If the number of ampere-turns is the same in each coil, then the force pulling on the iron bar in arrangement A is only a small fraction of the force exerted on the bar in arrangement B. The reluctance in the wood mount in A is so large that a greater number of ampere-turns is required for A to equal the amount of flux produced by B, which has an iron mount.
Core Design
Many DC electromagnets are solid bars or rods. However, the magnets for DC vibrators, motors, and generators and for AC equipment are an assembly of thin sheets of iron called laminations. For this type of magnet, the magnetic fields are in motion; that is, the lines of force whip back and forth as the current is turned on or off or is reversed.
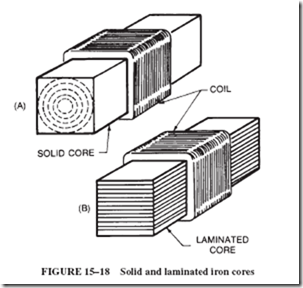
Whenever lines of force pass through any kind of metal, they tend to generate a cur- rent in the metal. For example, the dotted line in Figure 15–18A indicates the current that is generated inside the iron core of the electromagnet each time the amount or direction of the current in the coil is changed. The generated current is called an eddy current. An eddy current is considered to be a nuisance, because it takes energy from the coil circuit and heats the iron core.
The magnet core in Figure 15–18B consists of a stack of thin sheets of insulated iron. Only a small amount of current can circulate within the laminations of this type of core because of the poor electrical contact between the sheets. The small amount of electrical contact between the sheets is due to a coating of insulating lacquer on each sheet and the buildup of iron oxide on the sheets.
If eddy currents can be prevented, the loss of energy and the production of heat can be reduced. Iron containing a small amount of silicon is used for the core laminations because this combination possesses high permeability and high electrical resistance. A high electrical resistance in a core material hinders the formation of eddy currents in the core material.
Demagnetizers
Occasionally, it may be necessary to demagnetize an object. This is accomplished by placing the object into a varying magnetic field powered by a source of alternating cur- rent. This procedure will upset the orderly alignment of the atoms within the object to be demagnetized.
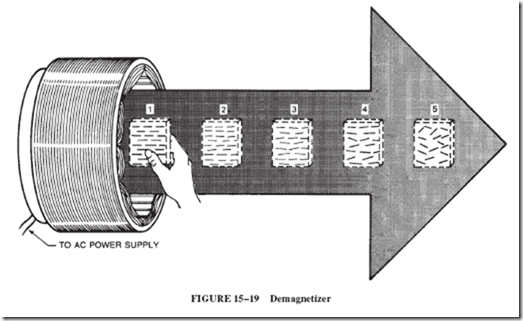
To illustrate the procedure, we are using a convenient demagnetizer fashioned from the stator winding of a small discarded motor. This winding is then connected to an AC power line through a current-limiting resistor, as shown in Figure 15–19.
In Figure 15–19, at position 1, a piece of steel is being magnetized; that is, the upper end of the steel piece is changing from north to south and back again at the rate of 60 times per second on an AC line. The piece of steel is now moved away from the coil to position 2. The steel is still being magnetized 60 times per second but not as strongly as at position 1. At position 3, the magnetizing effect is weaker and at position 4, weaker still, with the upper end of the steel piece alternating between a very weak north and a very weak south. By the time the steel piece reaches position 5, the magnetizing force of the coil is so weak that the steel atoms are left in general disarrangement and the steel piece is no longer magnetized.
Residual Magnetism
After an electromagnet has been de-energized (power turned off ), a ferromagnetic core is not completely demagnetized. The core has retained some of the magnetism. This is known as residual magnetism. The amount of residual magnetism depends on the retentivity of the steel used. Generally speaking, hard steels have a high degree of retentivity as opposed to soft iron, which has low retentivity.
In some instances, residual magnetism may be considered a nuisance factor. In some applications, however, the residual magnetism is a desirable and necessary characteristic of the appliance.
SUMMARY
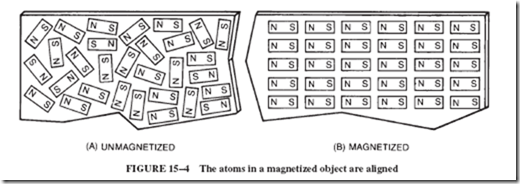
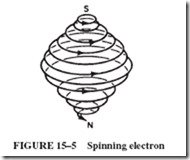
• All magnetism is due to electron motion, either the movement of electrons as they pass through a coil or the spinning motion of electrons in atoms.
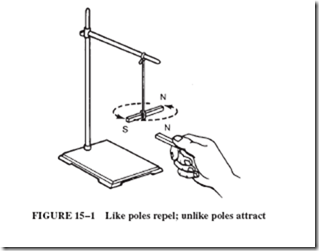
• Like poles repel; unlike poles attract.
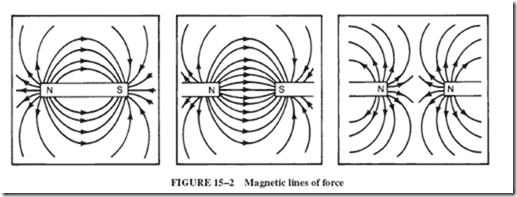
• The strength of a magnetic field is represented by the density of the lines of force. The direction of the field means the direction in which the north pole of a compass points.
• Most materials are nonmagnetic. The spinning of the electrons in the atoms of iron, nickel, and some alloys and oxides makes them magnetic.
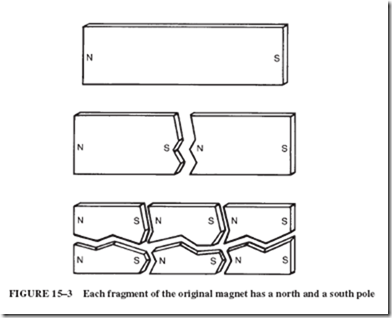
• Atoms of iron are little permanent magnets. The magnetizing of a piece of iron is a matter of arranging these atoms so that like poles face in the same direction.
• The left-hand rule for a single wire states that the thumb is in the direction of electron flow and the fingers are in the direction of the magnetic field.
• The left-hand rule for a coil states that the thumb is at the north pole and the fingers point in the direction of the electron current.
• Parallel currents in the same direction attract; parallel currents in opposite directions repel.
• The magnetic strength of a coil can be measured in ampere-turns (amperes 3 turns).
• Permeability is the ability of a material to become magnetized. Residual magnetism is the flux density that is retained in the material after the magnetizing force is removed. Coercive force is a magnetizing force applied in the opposite direction to demagnetize the material.
• A magnetic field contains useful energy.
• Moving electrons exert force on magnets; moving magnets exert force on electrons.
• Maintaining the strength of a permanent magnet depends on:
1. The type of alloy
2. Avoidance of excessive heat, shock, and AC magnetic fields
3. The presence of an iron core between the poles
• It is easy to remagnetize a permanent magnet.
• The magnetizing force of a coil depends on the number of ampere-turns per inch of the magnetic circuit. Equal magnetizing forces can be produced by large current and few turns or by small current and many turns.
• The complete path of lines of force through a magnet, the iron that the magnet attracts, the air, and so on are called the magnetic circuit.
• The opposition to the passage of flux lines in a magnetic circuit is called reluctance.
Magnetizing force in ampere-turns/inch
• Total number of lines of force 5 Reluctance of the magnetic circuit
• The use of laminated cores prevents energy loss due to eddy currents.
• Silicon steel is preferred to ordinary steel for laminated magnet cores because of its improved permeability and low eddy current energy loss.
Achievement Review
1. Naturally magnetic metals are called ferromagnetic materials. There are only three of these. Name them.
2. Explain the ferro in ferromagnetic.
3. How can a ferromagnetic metal be magnetized? Explain two methods.
4. The theory of magnetic domains explains the difference between magnetic and nonmagnetic substances. Draw a neat sketch and write a few brief sentences explaining this theory.
5. State the magnetic laws of attraction and repulsion.
6. Review your knowledge of electrostatic fields. How do those forces compare to the forces of magnetism? Explain.
7. Explain three ways to demagnetize a magnet.
8. Draw a neat sketch of a magnetic field around a bar magnet.
9. Flux lines have a specific direction. They are assumed to leave the pole and enter into the pole.
10. Magnetic lines of force will not cross one another. True or false?
11. What is reluctance? Explain.
12. Magnetic lines of flux can pass through all materials, even those that have no magnetic properties. True or false?
13. In Figure 15–9 you see pictures of concentric circles that resemble a rifle target of sorts. Explain
a. What these drawings represent
b. The significance of the innermost circle (containing a dot or cross mark)
c. The significance of the dot and the cross mark
14. What happens when a coil or wire is connected to a source of direct current?
15. What happens to a piece of steel when it is placed in a coil that is connected to a source of direct current?
16. Name at least 10 electrical devices that use electromagnets.
17. What effect does the steel core have on the magnetic field of an electromagnet?
18. There are two left-hand rules. How do they differ from each other?
19. Explain, in your own words, the left-hand rule for straight conductors.
20. Explain, in your own words, the left-hand rule for coils.
21. Name three factors that determine the strength of an electromagnet.
22. What happens to an electromagnet when the current through the coil is reversed?
23. Explain the word solenoid.
24. For what are solenoids used? Explain. Name some practical applications.
25. Solenoid cores are generally constructed from a soft iron rather than hard steel.
Why is soft iron preferred? (Explain this in terms of magnetic domains as explained in Figure 15–4.)
26. What effect, if any, does the polarity of a solenoid have on its electromagnetic strength?
27. How would the electromagnetic power of a solenoid be affected if one added:
a. More insulation to the wire?
b. More resistance to the solenoid circuit?