science universe

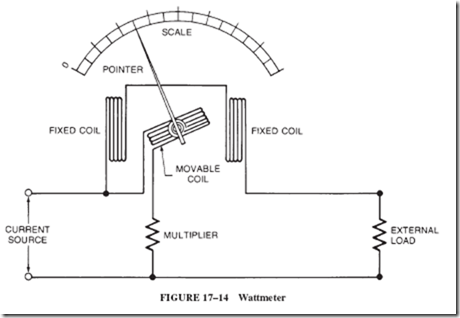
19–6 THREE TYPES OF SELF-EXCITED GENERATORS (SERIES, SHUNT, AND COMPOUND)

The Series Generator

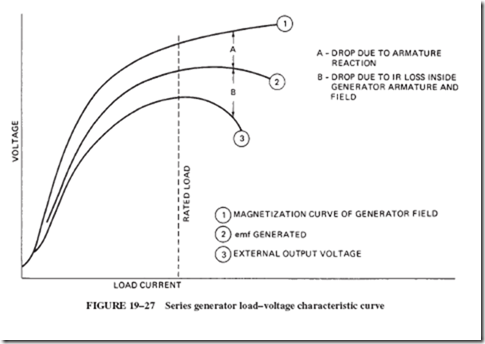
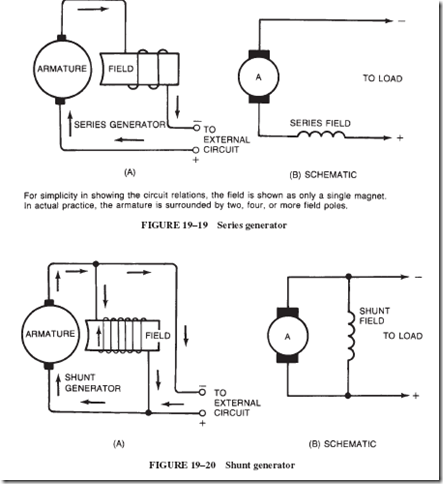
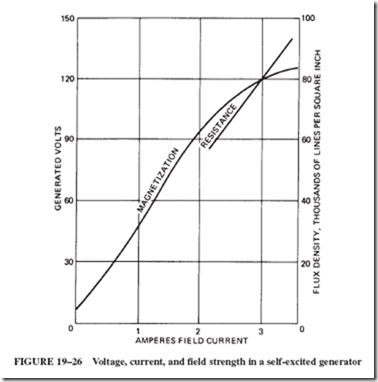
Look back at Figure 19–19 and recall that the field of the series generator carries the entire load current to the external circuit; therefore, the greater the load current, the greater the magnetic field strength; see Figure 19–27. If the generator is started with the external circuit disconnected from the generator terminals, there is no buildup of field. The small voltage due to residual magnetism cannot produce any current at all in an open circuit. If a small load current is taken from the generator, its output voltage is low. If a reasonably high load current is taken, the output voltage is high. If an ordinary parallel- wired lighting circuit is used as the load and two or three lamps turned on, the lamps are dim. The more lamps that are turned on, the brighter each lamp becomes. However, a little

of this voltage-increasing effect can be a good thing; it illustrates the effect of the series field of a cumulative compound generator; see Figure 19–27. The series generator, impractical for most jobs, does have one interesting application: It can be used in a simple motor-control system, driving a series motor at nearly constant speed with changing load on the motor (Chapter 21).

The Shunt Generator

We have seen, in Figure 19–20, that a shunt generator has its field winding connected parallel to the armature. Comparing this arrangement with that of the series generator, we find that the shunt field coil is constructed of many turns of relatively thin wire. Recall that magnetic field strength is proportional to the number of ampere-turns; thus, the shunt field coil requires relatively little current, generally amounting to less than 3% of the total current supplied by the armature.

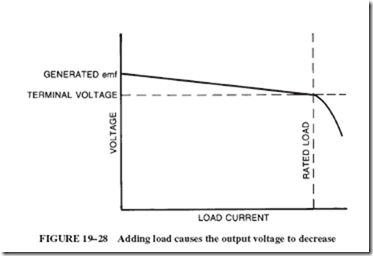
With the field coil parallel to the armature, it is reasonable to expect a stable output voltage as long as the generator is driven at constant speed. This is true, indeed, except that the voltage is gradually reduced as the load on the generator is increased; see Figure 19–28.

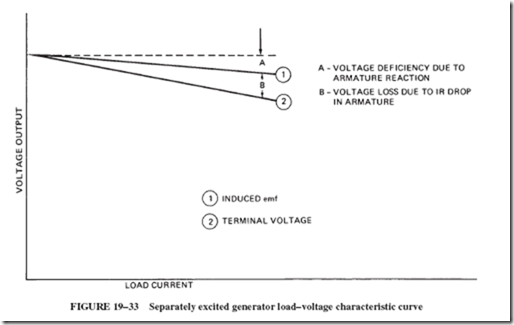
In our discussion, we distinguish between the generated emf (when the generator is unloaded) and the terminal voltage (delivered to the load). The difference between these two values represents the drop in output voltage that accompanies the increase in load current. This reduction in voltage is due to two factors, as follows:

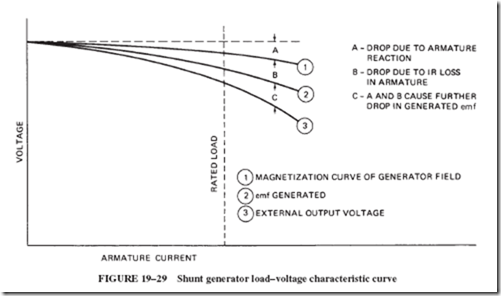
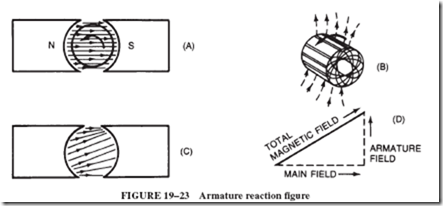
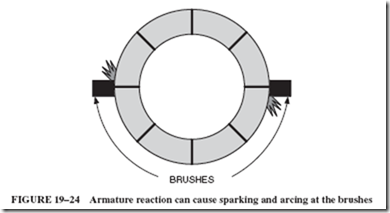
1. Armature reaction weakens the field, thereby decreasing the generated emf; see Figure 19–29 (drop A).

2. The IR drop of the armature. There is only a little resistance in the armature winding but enough to cause a voltage drop (IR drop). This IR drop, which varies proportionally with the load current, is lost to the load and causes a further reduction in output voltage; see Figure 19–29 (drop B).

Both of these effects reduce the output voltage. Reduced output voltage causes reduced field current and therefore field flux. With reduced field flux, there is a further reduction in generated emf; see Figure 19–29 (drop C).

Assume that we have a shunt generator with armature resistance equal to 0.4 ohm, rated 10-ampere output current. When operating with no load (external circuit open), we find that the emf is 121 volts. When operated at its rated 10-ampere load, there is a 4-volt drop, or waste, in the armature. (E 5 IR 5 10 3 0.4 5 4 V. Four volts are used in pushing electrons through the generator itself.) This 10-ampere load in the armature also distorts and weakens the field so that there is a decrease in the generated emf of 3 volts. Because of all these voltage deficiencies, the field current and flux are reduced; thus, the generated emf is less by another 4 volts. Because of armature reaction and reduced field current, 121 2 7 5 114 volts are generated. After subtracting the 4 volts used in the armature, there is an output voltage at the terminal of 110 volts.

The characteristic of shunt generators dropping their voltage with increased load is not all bad. In extreme cases of overload, such as a short circuit, the generator will pro- tect itself from damage by reducing the field excitation and, correspondingly, the output voltage. For example, if the generator is overloaded to 15 amperes instead of 10 amperes, increased armature reaction and the resulting reduction in field current bring the generated emf down to 109 volts. Fifteen amperes through the 0.4-ohm armature use 6 volts, so the terminal voltage is down to 103 volts.

Voltage Regulation

As a measurable quantity, the term voltage regulation means the percentage change of voltage from rated-load to no-load conditions.

The Compound Generator

The compound generator is designed to compensate for the voltage losses that characterize shunt generators under the influence of increased load. Recall that in a series generator, just the opposite phenomenon occurs: The voltage increases with increasing load. By adding a series winding to the shunt generator, we can combine the features of both windings to provide a more stable output voltage.

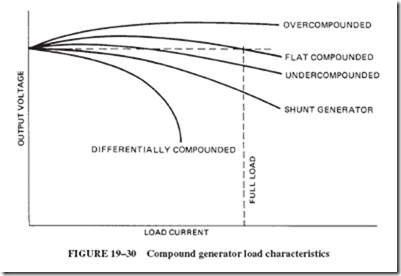
Let us examine the effect of adding series field coils to the shunt generator described previously. At a 10-ampere load with a series field coil present, we still have the field- weakening effect of armature reaction and the 4-volt IR drop on the armature, plus a possible 1-volt additional IR drop in the series field. All of these effects can be overcome by adding enough turns of the wire to the field. These turns are connected in series with the load; thus, the 10 amperes in these turns can add to the magnetizing effect of the shunt field coil, increasing the generated emf. The generated emf can readily be brought up to 126, which, less the 5-volt internal IR drops, makes the output voltage 121, the same as at no load. A generator with open-circuit voltage equal to rated load voltage is called flat compounded; see Figure 19–30.

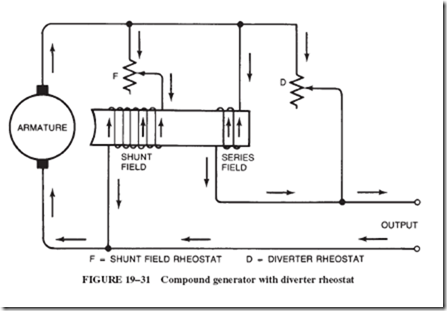
A generator can be overcompounded. Enough series ampere-turns can be provided to make the output voltage rise above no-load voltage as the output current increases. (Compare with series generators.) Usually, compound generators are built with enough series turns to accomplish overcompounding. The user can adjust the current in the series winding to suit specific operating conditions. Adjustment of the diverter rheostat allows some load current to bypass the series coils, as illustrated in Figure 19–31, and thereby to change the degree of compounding. For instance, if the effect of the series coil is severely limited, the shunt coil will dominate the output characteristics of the generator. Such a machine is said to be undercompounded.

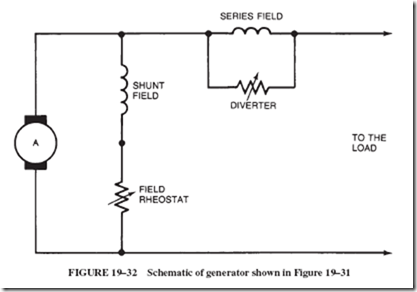
The same circuit of Figure 19–31 is shown schematically in Figure 19–32 to illustrate two points.

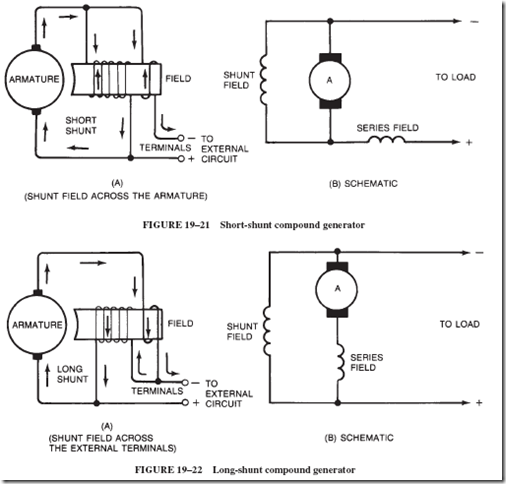
1. The generator is connected as a short-shunt generator. Remember, compound generators can be connected either in a short-shunt or long-shunt configuration.

2. The drawing shows a rheostat in the shunt field circuit for the purpose of varying the output voltage. As explained earlier in this chapter, with this rheostat, the operator can weaken or strengthen the magnetic field, thereby changing the output voltage of the generator.

Before leaving the subject of compound generators, let us have another look at Figure 19–30, and note the term differentially compounded. Most generators are cumulatively compounded; that is, the two windings on the pole pieces (series and shunt) are wound in the same direction, so that their magnetic fields will reinforce each other; see Figure 19–31. In a differentially compounded generator, by contrast, the two magnetic fields are opposing each other. Not many generators are differentially compounded.

19–7 SEPARATELY EXCITED GENERATORS

Two general ways of providing a magnetic field for a generator have been mentioned:

1. Permanent magnet (very limited application)

2. Self-excitation—shunt, series, or compound (the most widely used method)

A third possibility is a separate current source energizing the field coils of the generator, as illustrated in Figure 19–33. Normally, this method is used only as a part of a specialized motor-control circuit, such as Ward Leonard system, Rototrol system, or Amplidyne control system, to name a few. The purpose of these systems is to permit the operator to select any specific speed, after which the system holds the motor at that speed regardless of variations in the load on the motor. Separate excitation systems of this type are used in mine hoists, steel-mill rolling mills, paper machines, diesel-electric locomotives, and other similar devices.

19–8 GENERATOR CALCULATIONS

The following paragraphs are not intended to provide enough details to illustrate all of the factors that must be calculated by a generator designer. They are intended only to point out the basic principles of the energy conversion that goes on in a generator.

Generator emf

As stated before, generator emf is proportional to field strength, number of wires on the armature, and rpm of the armature. When the field strength, armature windings, and rpm of the armature are known, the number of lines of force cut per second can be found. The cutting of 100,000,000 lines by wire each second makes 1 volt.

EXAMPLE 19–1

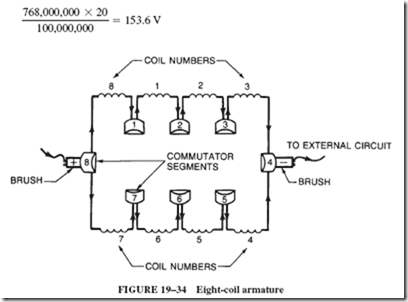
Given: An armature as shown in Figure 19–34. (This is similar to the armature in Figures 19–13 and 19–14.) The armature has eight coils, each coil consisting of

40 turns, operating at 1,200 rpm, between two field poles, each pole having 15 square inches of face area and a flux density of 80,000 lines per square inch.

Find: The emf generated.

Solution

Figure 19–34 shows that the coils are in two parallel groups, with four coils in series in each group. The emf is produced by four coils in series, not eight. Therefore, we need to take into account four coils of 40 turns each 5 160 turns. Since the purpose of this calculation is to find the average emf, we need not be concerned about differences in instantaneous voltages in the coils.

Each turn of wire in the coil has two sides, both of which cut the entire field twice (once up and once down) during each revolution. The 160 turns, then, have to be multiplied by 4 to give the number of times that the entire field is cut by wire each revolution. The field is cut 640 times.

The total field flux is 80,000 lines per sq in. 3 15 sq in. 5 1,200,000 lines. During one rotation, 1,200,000 lines are cut 640 times: 640 3 1,200,000 5 768,000,000 total lines of force cut.

The coils rotate at 1,200 rpm, which is 20 revolutions per second. The total cutting of lines per second is 768,000,000 times 20. The emf generated is

Planning a generator design to produce a given emf involves a sensible choice of turns, flux, rpm, and type of winding—based on both theory and experience—and takes into account any special demands on the generator in use.

Emf vs.Terminal Voltage

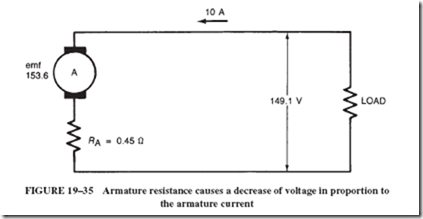
The emf that we just calculated in the preceding problem is not the same as the voltage delivered to the terminals of the load. To understand why, consider the following: The armature has some resistance, say 0.4 ohm; and the brushes, riding on the commutator, have resistance of about 0.05 ohm. These resistances are shown as RA, lumped together outside the armature, in the schematic diagram of Figure 19–35.

Assuming that 10 amperes is flowing through the armature, there will be a voltage drop of 4.5 volts in the armature, which is lost to the load. Think of it as a series circuit, and you will see that only 149.1 volts will be available at the terminals of the load.

Kirchhoff’s voltage law is proven once again and is stated now like this:

Output voltage = Generated emf – IR drop in armature and brushes

19–3 GENERATOR FIELD STRUCTURES

DC generators can be classified by the method used for providing the magnetic field. This classification can be tabulated like this:

1. Permanent-magnet generators

2. Separately excited generators

3. Self-excited generators

a. Shunt generators

b. Series generators

c. Compound generators

Permanent-magnet generators are reserved for a few low-power applications where control of field strength is not needed. Such constant-field generators are useful in control devices or circuits. In such applications, use is made of the permanent magnet generator’s characteristic to deliver a voltage output proportional to its speed.

Permanent-magnet generators are also known as magnetos and find applications with the electrical systems of motorcycles, small tractors, lawn mower engines, and the like.

The field structure of a permanent-magnet generator is similar in design to that shown in Figure 19–1. Generally, though, electromagnets are used instead of permanent magnets. In this case, the circular frame, or yoke, is fitted with laminated iron pole pieces to accommodate the field winding, as illustrated in Figures 19–16 and 19–17.

Look at these drawings and note how the magnetic poles are developed in accordance with the left-hand rule for coils and the direction of the electron current. Furthermore, note that the magnetic circuit is completed by the iron yoke, or frame, which carries and concentrates the lines of magnetic flux. Note the positive and negative polarity marking on the wires that supply the field coils. It is the electric polarity of the power source that determines the direction of the current flow and, therefore, the orientation of the magnetic poles.

This is shown by the schematic diagram in Figure 19–18. If these field coil wires are attached to a storage battery or to a rectifier, the generator is an externally excited or a separately excited generator.

Field Connections for Self-Excited Generators

There are three possible field connections for self-excited generators, energized by current generated in the armature of the same machine.

1. Series: The field coils can be in series with the external load circuit. Series coils consist of relatively few turns of large wire, since they must carry the entire output current. Of the three types, this series generator is used least often; see Figure 19–19.

2. Shunt (or parallel): The field coils are connected across the brushes of the generator, which puts the coils in parallel with the external load. Shunt coils consist of a large number of turns of small wire and carry only a small current; see Figure 19–20.

3. Compound: The field-magnet iron is magnetized by the combined effect of two sets of coils. One set of low-resistance coils is in series with the external load circuit, and one set of high-resistance coils is in parallel with the load circuit.

In both of the compound generators shown in Figures 19–21 and 19–22, the series field aids the shunt field in magnetizing effect. This is the usual arrangement, called cumulative compounding. In a less common arrangement called differential compounding, the fields are connected so that they oppose each other.

19–4 ARMATURE REACTION

Ideally, the magnetic field in a generator has a straight, uniform pattern, as shown in Figure 19–23A. But the current generated in the armature causes another magnetic field, shown in B. Both magnetic fields combine (main field and armature field), making the total magnetic field take the direction shown in C. The distortion, or bending, of the main magnetic field of the generator, caused by the magnetic field of the current in the armature, is called armature reaction. Unless the distortion is corrected when the armature is producing current, the actual field in the generator is twisted, as shown in Figure 19–23D.

The Ill Effects of a Twisted Field

The bunching of the lines at the corners of the field poles causes an irregularity in the voltage output. More importantly, the field iron is not used effectively, and the total flux is less, making the average voltage output low.

Furthermore, the twisted field changes the timing of the current reversals in the armature coils. In the explanation of Figures 19–13 and 19–14, it is stated that no harm is done by the brushes at certain instants when emf is not generated in the coil connected to the pair of segments involved. That statement is true only if the magnetic field is not disturbed. When the field is distorted, there is an emf between the commutator segments at the instant when both touch the same brush. This emf generates a brief, high current that causes excessive sparking and arcing as the commutator rotates; see Figure 19–24.

Remedies

Rotation. The first remedy used for field distortion was to rotate the brush holder by an equal amount to the twisting of the field. The rotation caused commutator segments to break contact with the brush at the instant of no emf. This remedy was unsatisfactory

because the amount of the field distortion changes whenever the armature current (load current) changes. To improve commutation in a generator, the brush holder is turned forward in the direction of rotation of the armature. To improve commutation in a motor, the brush holder is turned backward.

Interpoles. A better remedy is the addition of small field poles, called interpoles, or commutating poles, between the main field poles. Previous sketches show the armature current causing a vertical upward flux that tips the main magnetic field. The interpoles create another downward flux that tends to tip the main field back where it belongs. The interpole coils of the generator are connected into the circuit so that the interpoles have the same polarity as the main poles directly ahead of them (ahead in the sense of direction of armature rotation). In Figure 19–25, if rotation is reversed, the polarity of the interpoles must be reversed also.

To make the strength of the interpoles appropriate for their changing duty as the armature and load current changes, the interpoles are energized by coils in series with the armature. They therefore carry the same current as the armature. Since interpoles take care of the commutator difficulties, stationary brush holders can be used, with the brushes at the geometrical axis as shown originally.

Compensating Winding. However, these interpoles overcome field distortion only in their immediate neighborhood; much of the overall field-weakening effect is still present.

Large generators carry their output current through a few wires lying in the pole face placed parallel to the armature wires. This pole-face winding, called a compensating winding, is the most complete way of overcoming the field-weakening effect of armature reaction.

Advantages. Armature reaction can actually be advantageous in generators that must operate over a wide range of speeds. An example of this would be the DC generators that were used in automobiles of the 1920s through the 1950s. Consider the wide range of speeds encountered in a car engine. When field strength is constant, emf is proportional to rpm, a condition highly undesirable in the automotive generator. However, at moderate current output, the armature current distorts and weakens the average field sufficiently to help keep the emf at a reasonable value at high speed.

19–5 BUILDUP OF SELF-EXCITED FIELDS

The successful starting up of a generator depends on the existence of residual magnetism in the field iron; that is, a little magnetism remains from the effect of previous current in the field coil. When the armature of a shunt or compound generator starts rotating, a very low voltage is generated in the armature. This voltage is caused by the weak field in which the armature rotates. The low voltage causes a small current in the shunt field coils, increasing the strength of the field slightly. The increased field strength, in turn, causes the generated voltage to increase slightly. This increase causes more current in the field, increasing the field strength and therefore the armature voltage still more. The maximum amount of voltage, current, and field strength that can be built up is shown on the graph in Figure 19–26.

The magnetization curve, like that shown in Figure 19–26, shows the increase in field strength as the field current increases. Assume we have a generator, rated 120 volts output, that has a 40-ohm field coil. When the generator is started, the magnetization starts at a point above the zero line. This point represents a residual flux density of, say, 5,000 lines per square inch. According to the scales at the left, 5,000 lines per square inch cause a generated voltage of 7.5 volts when the armature is rotating at rated speed. The small current in the field (I 5 7.5/40 5 0.19 amperes) adds to the field strength, and the buildup continues to a field strength of 80,000 lines per square inch. By this time, the generated 120 volts is putting 3 amperes through the field. This 3-ampere current is needed to maintain the field at 80,000 lines per square inch in order for the 120 volts to be generated. At 3 amperes, because no more than 120 volts can be generated, the buildup stops. This limit is indicated by the resistance line on the graph. (Points on this resistance line give values of volts and amperes for 40-ohm resistance.)

The previous condition assumes constant speed. The generator output can be in- creased or decreased by increasing or decreasing the rpm. Also, the operating voltage of this shunt generator can be lowered to some other value (possibly 100 volts) by putting a little more resistance in the field circuit by using a rheostat in series with the field coil. Voltage output on a shunt generator is commonly controlled by such a field rheostat.

Failure to Develop Voltage

A generator without residual magnetism will fail to build up the magnetic field that is necessary to develop an output. Any of the following conditions may cause a self- excited generator to fail in producing the desired voltage:

• The direction of rotation may be such that it produces a magnetic field in the same direction as the residual magnetism. If the rotation is accidentally reversed, the generated field will oppose the residual magnetism and thereby obliterate it.

• A generator should not be started under load. If a load is attached before the generator develops its rated output, the terminal voltage may drop enough to cause a corresponding reduction in the field current, which in turn may cause a further decrease in the terminal voltage. This cycle of events continues until there is virtually no voltage output.

• Almost all generators have a rheostat connected in series with their shunt field winding for changing the output voltage by varying the field strength (excitation). Such a rheostat should be adjusted to its minimum resistance value during the start-up process, while the generator is building up its field.

• Also, accidental application of alternating current (AC) to the field coils will result in the loss of the residual magnetism that is so necessary for the buildup of the generator’s field. (Recall from Chapter 15 that AC acts as a demagnetizer.) In the event that the residual magnetism has been lost, it can be restored by a process known as flashing the field. This procedure requires a separate DC source to be applied briefly to the field coils. The voltage used for flashing the field should be nearly as high as the rated voltage for the generator. A 10- to 20-second application is generally sufficient.

19–3 GENERATOR FIELD STRUCTURES

DC generators can be classified by the method used for providing the magnetic field. This classification can be tabulated like this:

1. Permanent-magnet generators

2. Separately excited generators

3. Self-excited generators

a. Shunt generators

b. Series generators

c. Compound generators

Permanent-magnet generators are reserved for a few low-power applications where control of field strength is not needed. Such constant-field generators are useful in control devices or circuits. In such applications, use is made of the permanent magnet generator’s characteristic to deliver a voltage output proportional to its speed.

Permanent-magnet generators are also known as magnetos and find applications with the electrical systems of motorcycles, small tractors, lawn mower engines, and the like.

The field structure of a permanent-magnet generator is similar in design to that shown in Figure 19–1. Generally, though, electromagnets are used instead of permanent magnets. In this case, the circular frame, or yoke, is fitted with laminated iron pole pieces to accommodate the field winding, as illustrated in Figures 19–16 and 19–17.

Look at these drawings and note how the magnetic poles are developed in accordance with the left-hand rule for coils and the direction of the electron current. Furthermore, note that the magnetic circuit is completed by the iron yoke, or frame, which carries and concentrates the lines of magnetic flux. Note the positive and negative polarity marking on the wires that supply the field coils. It is the electric polarity of the power source that determines the direction of the current flow and, therefore, the orientation of the magnetic poles.

This is shown by the schematic diagram in Figure 19–18. If these field coil wires are attached to a storage battery or to a rectifier, the generator is an externally excited or a separately excited generator.

Field Connections for Self-Excited Generators

There are three possible field connections for self-excited generators, energized by current generated in the armature of the same machine.

1. Series: The field coils can be in series with the external load circuit. Series coils consist of relatively few turns of large wire, since they must carry the entire output current. Of the three types, this series generator is used least often; see Figure 19–19.

2. Shunt (or parallel): The field coils are connected across the brushes of the generator, which puts the coils in parallel with the external load. Shunt coils consist of a large number of turns of small wire and carry only a small current; see Figure 19–20.

3. Compound: The field-magnet iron is magnetized by the combined effect of two sets of coils. One set of low-resistance coils is in series with the external load circuit, and one set of high-resistance coils is in parallel with the load circuit.

In both of the compound generators shown in Figures 19–21 and 19–22, the series field aids the shunt field in magnetizing effect. This is the usual arrangement, called cumulative compounding. In a less common arrangement called differential compounding, the fields are connected so that they oppose each other.

19–4 ARMATURE REACTION

Ideally, the magnetic field in a generator has a straight, uniform pattern, as shown in Figure 19–23A. But the current generated in the armature causes another magnetic field, shown in B. Both magnetic fields combine (main field and armature field), making the total magnetic field take the direction shown in C. The distortion, or bending, of the main magnetic field of the generator, caused by the magnetic field of the current in the armature, is called armature reaction. Unless the distortion is corrected when the armature is producing current, the actual field in the generator is twisted, as shown in Figure 19–23D.

The Ill Effects of a Twisted Field

The bunching of the lines at the corners of the field poles causes an irregularity in the voltage output. More importantly, the field iron is not used effectively, and the total flux is less, making the average voltage output low.

Furthermore, the twisted field changes the timing of the current reversals in the armature coils. In the explanation of Figures 19–13 and 19–14, it is stated that no harm is done by the brushes at certain instants when emf is not generated in the coil connected to the pair of segments involved. That statement is true only if the magnetic field is not disturbed. When the field is distorted, there is an emf between the commutator segments at the instant when both touch the same brush. This emf generates a brief, high current that causes excessive sparking and arcing as the commutator rotates; see Figure 19–24.

Remedies

Rotation. The first remedy used for field distortion was to rotate the brush holder by an equal amount to the twisting of the field. The rotation caused commutator segments to break contact with the brush at the instant of no emf. This remedy was unsatisfactory

because the amount of the field distortion changes whenever the armature current (load current) changes. To improve commutation in a generator, the brush holder is turned forward in the direction of rotation of the armature. To improve commutation in a motor, the brush holder is turned backward.

Interpoles. A better remedy is the addition of small field poles, called interpoles, or commutating poles, between the main field poles. Previous sketches show the armature current causing a vertical upward flux that tips the main magnetic field. The interpoles create another downward flux that tends to tip the main field back where it belongs. The interpole coils of the generator are connected into the circuit so that the interpoles have the same polarity as the main poles directly ahead of them (ahead in the sense of direction of armature rotation). In Figure 19–25, if rotation is reversed, the polarity of the interpoles must be reversed also.

To make the strength of the interpoles appropriate for their changing duty as the armature and load current changes, the interpoles are energized by coils in series with the armature. They therefore carry the same current as the armature. Since interpoles take care of the commutator difficulties, stationary brush holders can be used, with the brushes at the geometrical axis as shown originally.

Compensating Winding. However, these interpoles overcome field distortion only in their immediate neighborhood; much of the overall field-weakening effect is still present.

Large generators carry their output current through a few wires lying in the pole face placed parallel to the armature wires. This pole-face winding, called a compensating winding, is the most complete way of overcoming the field-weakening effect of armature reaction.

Advantages. Armature reaction can actually be advantageous in generators that must operate over a wide range of speeds. An example of this would be the DC generators that were used in automobiles of the 1920s through the 1950s. Consider the wide range of speeds encountered in a car engine. When field strength is constant, emf is proportional to rpm, a condition highly undesirable in the automotive generator. However, at moderate current output, the armature current distorts and weakens the average field sufficiently to help keep the emf at a reasonable value at high speed.

19–5 BUILDUP OF SELF-EXCITED FIELDS

The successful starting up of a generator depends on the existence of residual magnetism in the field iron; that is, a little magnetism remains from the effect of previous current in the field coil. When the armature of a shunt or compound generator starts rotating, a very low voltage is generated in the armature. This voltage is caused by the weak field in which the armature rotates. The low voltage causes a small current in the shunt field coils, increasing the strength of the field slightly. The increased field strength, in turn, causes the generated voltage to increase slightly. This increase causes more current in the field, increasing the field strength and therefore the armature voltage still more. The maximum amount of voltage, current, and field strength that can be built up is shown on the graph in Figure 19–26.

The magnetization curve, like that shown in Figure 19–26, shows the increase in field strength as the field current increases. Assume we have a generator, rated 120 volts output, that has a 40-ohm field coil. When the generator is started, the magnetization starts at a point above the zero line. This point represents a residual flux density of, say, 5,000 lines per square inch. According to the scales at the left, 5,000 lines per square inch cause a generated voltage of 7.5 volts when the armature is rotating at rated speed. The small current in the field (I 5 7.5/40 5 0.19 amperes) adds to the field strength, and the buildup continues to a field strength of 80,000 lines per square inch. By this time, the generated 120 volts is putting 3 amperes through the field. This 3-ampere current is needed to maintain the field at 80,000 lines per square inch in order for the 120 volts to be generated. At 3 amperes, because no more than 120 volts can be generated, the buildup stops. This limit is indicated by the resistance line on the graph. (Points on this resistance line give values of volts and amperes for 40-ohm resistance.)

The previous condition assumes constant speed. The generator output can be in- creased or decreased by increasing or decreasing the rpm. Also, the operating voltage of this shunt generator can be lowered to some other value (possibly 100 volts) by putting a little more resistance in the field circuit by using a rheostat in series with the field coil. Voltage output on a shunt generator is commonly controlled by such a field rheostat.

Failure to Develop Voltage

A generator without residual magnetism will fail to build up the magnetic field that is necessary to develop an output. Any of the following conditions may cause a self- excited generator to fail in producing the desired voltage:

• The direction of rotation may be such that it produces a magnetic field in the same direction as the residual magnetism. If the rotation is accidentally reversed, the generated field will oppose the residual magnetism and thereby obliterate it.

• A generator should not be started under load. If a load is attached before the generator develops its rated output, the terminal voltage may drop enough to cause a corresponding reduction in the field current, which in turn may cause a further decrease in the terminal voltage. This cycle of events continues until there is virtually no voltage output.

• Almost all generators have a rheostat connected in series with their shunt field winding for changing the output voltage by varying the field strength (excitation). Such a rheostat should be adjusted to its minimum resistance value during the start-up process, while the generator is building up its field.

• Also, accidental application of alternating current (AC) to the field coils will result in the loss of the residual magnetism that is so necessary for the buildup of the generator’s field. (Recall from Chapter 15 that AC acts as a demagnetizer.) In the event that the residual magnetism has been lost, it can be restored by a process known as flashing the field. This procedure requires a separate DC source to be applied briefly to the field coils. The voltage used for flashing the field should be nearly as high as the rated voltage for the generator. A 10- to 20-second application is generally sufficient.

18–4 LENZ’S LAW

There is a more fundamental way of determining the current direction. As pointed out before, electrical energy is produced by mechanical energy; the hand that removes the magnet from the coil must do some work. The magnet does not push out of the coil by itself; the hand must pull it out.

The coil itself, however, makes it difficult to move the magnet. It creates magnetic poles of its own that oppose the motion of the hand. Figure 18–6 shows the magnet a little more removed from the coil than in Figure 18–5. The induced current in the coil is in such a direction as to develop poles in the coil as shown. (Recall the left-hand rule for a coil.) The attraction of these opposite poles pulls the magnet toward the coil.

If the motion of the magnet is reversed, that is, pushed into the coil, the induced current reverses also, developing poles on the coil that repel the approaching magnet.

This general idea was recognized years ago by Heinrich Lenz and is summarized in Lenz’s law:

An induced voltage or current opposes the motion that causes it.

Lenz’s law is also useful in determining induced current direction in more complex machinery. Note that in Figures 18–3 and 18–5 the coil is surrounded by the magnetic field of the bar magnet. Removing the magnet removes this magnetic field. The induced current in the coil tries to maintain a field of the same strength and direction as the field

that is being removed; see Figure 18–7. (Apply the left-hand rule to the coil in Figure 18–6 to determine direction and shape of the field of the coil due to current in it.)

There is another way of looking at Lenz’s law. Originally, the coil in Figure 18–8 had no magnetic field in it. As the approaching magnet’s lines of force enter the coil, the coil develops a field of its own that tends to restore conditions in the coil to the original zero-field condition, that is, tends to cancel out the oncoming field. Therefore, there is an alternate way of stating Lenz’s law:

An induced voltage or current opposes a change of magnetic field.

In the preceding discussion, the terms induced voltage and induced current seem to have been used interchangeably. One should understand that the relative motion of wire and magnetic field always induces a voltage, or emf. If there is a closed circuit, this induced emf causes a current.

18–5 INDUCTION IN ROTATING MACHINES

Commercial generators produce electrical energy either by rotating coils of wire in a stationary magnetic field or by rotating a magnet inside a stationary coil of wire. Let us explore the rotation of a coil within a magnetic field. To analyze this action, we are going to reduce the coil to one single loop and examine the result of its rotation for one revolution. The single loop shown in Figure 18–9 represents the concept of such a simple generator.

Mechanical energy must be expended to rotate this coil within the magnetic field and cut the lines of flux. In practical applications, such energy is provided by turbines or engines called prime movers.

As the coil is rotated, an emf is induced, which appears between the two ends of the loop. Two metal bands, called slip rings, are attached to these ends to facilitate the transfer of this voltage to an external load. Carbon brushes riding on these smooth metal rings conduct the generated electricity to the circuit, where it can be utilized.

The voltage generated in this manner continually changes in magnitude and direction. Such emf is known as alternating voltage and can be made visible on an instrument known as the oscilloscope. The pattern displayed is called a sine wave, which shows the variations of the ever-changing voltage as the coil is rotated for one complete revolution.

Figure 18–10 shows such a sine wave, representing the voltage output generated during one revolution. Note the voltage scale to the left of the curve showing both positive and negative values. The sine wave shows how these values change with respect to the angle of rotation through which the coil has traveled. (One circle of rotation 5 360 degrees.)

In tracing this curve, we find moments when the voltage output is 0. This happens every 180 degrees, when the cutting edge of the coil moves parallel to the lines of flux, Figure 18–9. By contrast, when the cutting edges move perpendicular to the flux lines

(beneath the poles), the rate of cutting flux lines—and therefore the voltage output—is at its maximum. This is shown at the 90-degree and 270-degree points of the sine wave.

Recall that not all generators are designed to rotate coils within a magnetic field but, instead, rotate a magnet within a stationary coil. The largest generators built contain stationary coils in which useful current is induced by a rotating magnet. Figure 18–11 shows one stationary coil. The cylindrical object shown within the coil represents a rotating magnet that is magnetized along a diameter.

Let us assume that this cylindrical magnet is rotated within the coil and, as the magnetic poles revolve, its flux lines are cut by the stationary conductors of the coil. Such rotation produces an alternating current, just as the repeated motion of the wire in Figure 18–1 produces AC.

To stress an important point once more, we can state that one such revolution produces one cycle of alternating voltage output in the form of a sine wave. Commercial generators in the United States are standardized to produce 60 cycles per second. This standard is known as the frequency of the power supply.

As you progress in your study of electricity, you will learn more about AC. What you need to know at this time is that the induction process in rotating machines produces AC. If direct current (DC) is needed, it can be obtained from AC by using rectifiers.

DC generators achieve rectification by using a commutator instead of slip rings. This is one of the facts to be presented in the next chapter.

SUMMARY

• The voltage produced by generators is called induced emf. This emf is produced either by the motion of wires across a magnetic field or by the motion of a magnetic field across wires.

• This induction process in a generator converts mechanical energy into electrical

energy.

• The amount of induced emf depends on the strength of the magnetic field, the number of turns of wire in the device, and the speed of motion.

• To produce 1 volt, the wire must cut 100,000,000 lines of flux per second.

• Lenz’s law: An induced voltage or current opposes the motion that causes it. An in- duced voltage or current opposes a change of magnetic field.

• Alternating current is generated in stationary coils when a magnet is rotated inside the coil.

• Alternating current is generated in a coil when the coil is rotated in a stationary magnetic field. By means of a commutator, this current is fed into the outside circuit as direct (one-way) current.

Achievement Review

1. A wire is moved through a field, as in the sketch below. What is the direction of the induced emf?

2. In a generator, from where does the electrical energy come?

3. The electric automobile of 1912 was powered only by storage batteries and an electric motor. The necessity of frequent battery charging helped make these cars obsolete. Could a generator, belt-driven from the wheels of a trailer, charge the batteries to make longer trips possible?

4. State three factors on which the amount of induced voltage depends.

5. In a certain generator, like that shown in Figure 18–11, the loop of wire en- closes 10,000 lines of force. What is the total number of lines of force cut during one complete rotation of the magnet?

6. If the magnet of the generator in Figure 18–11 is rotated at a speed of 2,400 rpm, how many lines of force are cut each second? How much voltage is produced?

7. In the generator in the sketch below, determine which brush is positive and which is negative.

8. State Lenz’s law. State the left-hand generator rule. Which one of these is the more important fundamental principle?

9. Figure 18–5 shows a magnet being pulled out from a coil to the right. If the magnet is pulled out to the left, is the induced current in the same direction as shown? Explain your answer.

10. A copper disk is supported between magnet poles so it can be rotated, as shown in the sketch. What happens in the disk as it rotates?

11. Does the strength of the magnet in the previous sketch have any effect on the amount of force needed to turn the disk?

12. A coin spinning on the end of a thread is lowered into a magnetic field. Explain what happens and why it does happen.

13. An aluminum cup is hung upside down on a pivot over a rotating magnet, as shown in the sketch below. Explain what happens to the cup.

18–4 LENZ’S LAW

There is a more fundamental way of determining the current direction. As pointed out before, electrical energy is produced by mechanical energy; the hand that removes the magnet from the coil must do some work. The magnet does not push out of the coil by itself; the hand must pull it out.

The coil itself, however, makes it difficult to move the magnet. It creates magnetic poles of its own that oppose the motion of the hand. Figure 18–6 shows the magnet a little more removed from the coil than in Figure 18–5. The induced current in the coil is in such a direction as to develop poles in the coil as shown. (Recall the left-hand rule for a coil.) The attraction of these opposite poles pulls the magnet toward the coil.

If the motion of the magnet is reversed, that is, pushed into the coil, the induced current reverses also, developing poles on the coil that repel the approaching magnet.

This general idea was recognized years ago by Heinrich Lenz and is summarized in Lenz’s law:

An induced voltage or current opposes the motion that causes it.

Lenz’s law is also useful in determining induced current direction in more complex machinery. Note that in Figures 18–3 and 18–5 the coil is surrounded by the magnetic field of the bar magnet. Removing the magnet removes this magnetic field. The induced current in the coil tries to maintain a field of the same strength and direction as the field

that is being removed; see Figure 18–7. (Apply the left-hand rule to the coil in Figure 18–6 to determine direction and shape of the field of the coil due to current in it.)

There is another way of looking at Lenz’s law. Originally, the coil in Figure 18–8 had no magnetic field in it. As the approaching magnet’s lines of force enter the coil, the coil develops a field of its own that tends to restore conditions in the coil to the original zero-field condition, that is, tends to cancel out the oncoming field. Therefore, there is an alternate way of stating Lenz’s law:

An induced voltage or current opposes a change of magnetic field.

In the preceding discussion, the terms induced voltage and induced current seem to have been used interchangeably. One should understand that the relative motion of wire and magnetic field always induces a voltage, or emf. If there is a closed circuit, this induced emf causes a current.

18–5 INDUCTION IN ROTATING MACHINES

Commercial generators produce electrical energy either by rotating coils of wire in a stationary magnetic field or by rotating a magnet inside a stationary coil of wire. Let us explore the rotation of a coil within a magnetic field. To analyze this action, we are going to reduce the coil to one single loop and examine the result of its rotation for one revolution. The single loop shown in Figure 18–9 represents the concept of such a simple generator.

Mechanical energy must be expended to rotate this coil within the magnetic field and cut the lines of flux. In practical applications, such energy is provided by turbines or engines called prime movers.

As the coil is rotated, an emf is induced, which appears between the two ends of the loop. Two metal bands, called slip rings, are attached to these ends to facilitate the transfer of this voltage to an external load. Carbon brushes riding on these smooth metal rings conduct the generated electricity to the circuit, where it can be utilized.

The voltage generated in this manner continually changes in magnitude and direction. Such emf is known as alternating voltage and can be made visible on an instrument known as the oscilloscope. The pattern displayed is called a sine wave, which shows the variations of the ever-changing voltage as the coil is rotated for one complete revolution.

Figure 18–10 shows such a sine wave, representing the voltage output generated during one revolution. Note the voltage scale to the left of the curve showing both positive and negative values. The sine wave shows how these values change with respect to the angle of rotation through which the coil has traveled. (One circle of rotation 5 360 degrees.)

In tracing this curve, we find moments when the voltage output is 0. This happens every 180 degrees, when the cutting edge of the coil moves parallel to the lines of flux, Figure 18–9. By contrast, when the cutting edges move perpendicular to the flux lines

(beneath the poles), the rate of cutting flux lines—and therefore the voltage output—is at its maximum. This is shown at the 90-degree and 270-degree points of the sine wave.

Recall that not all generators are designed to rotate coils within a magnetic field but, instead, rotate a magnet within a stationary coil. The largest generators built contain stationary coils in which useful current is induced by a rotating magnet. Figure 18–11 shows one stationary coil. The cylindrical object shown within the coil represents a rotating magnet that is magnetized along a diameter.

Let us assume that this cylindrical magnet is rotated within the coil and, as the magnetic poles revolve, its flux lines are cut by the stationary conductors of the coil. Such rotation produces an alternating current, just as the repeated motion of the wire in Figure 18–1 produces AC.

To stress an important point once more, we can state that one such revolution produces one cycle of alternating voltage output in the form of a sine wave. Commercial generators in the United States are standardized to produce 60 cycles per second. This standard is known as the frequency of the power supply.

As you progress in your study of electricity, you will learn more about AC. What you need to know at this time is that the induction process in rotating machines produces AC. If direct current (DC) is needed, it can be obtained from AC by using rectifiers.

DC generators achieve rectification by using a commutator instead of slip rings. This is one of the facts to be presented in the next chapter.

SUMMARY

• The voltage produced by generators is called induced emf. This emf is produced either by the motion of wires across a magnetic field or by the motion of a magnetic field across wires.

• This induction process in a generator converts mechanical energy into electrical

energy.

• The amount of induced emf depends on the strength of the magnetic field, the number of turns of wire in the device, and the speed of motion.

• To produce 1 volt, the wire must cut 100,000,000 lines of flux per second.

• Lenz’s law: An induced voltage or current opposes the motion that causes it. An in- duced voltage or current opposes a change of magnetic field.

• Alternating current is generated in stationary coils when a magnet is rotated inside the coil.

• Alternating current is generated in a coil when the coil is rotated in a stationary magnetic field. By means of a commutator, this current is fed into the outside circuit as direct (one-way) current.

Achievement Review

1. A wire is moved through a field, as in the sketch below. What is the direction of the induced emf?

2. In a generator, from where does the electrical energy come?

3. The electric automobile of 1912 was powered only by storage batteries and an electric motor. The necessity of frequent battery charging helped make these cars obsolete. Could a generator, belt-driven from the wheels of a trailer, charge the batteries to make longer trips possible?

4. State three factors on which the amount of induced voltage depends.

5. In a certain generator, like that shown in Figure 18–11, the loop of wire en- closes 10,000 lines of force. What is the total number of lines of force cut during one complete rotation of the magnet?

6. If the magnet of the generator in Figure 18–11 is rotated at a speed of 2,400 rpm, how many lines of force are cut each second? How much voltage is produced?

7. In the generator in the sketch below, determine which brush is positive and which is negative.

8. State Lenz’s law. State the left-hand generator rule. Which one of these is the more important fundamental principle?

9. Figure 18–5 shows a magnet being pulled out from a coil to the right. If the magnet is pulled out to the left, is the induced current in the same direction as shown? Explain your answer.

10. A copper disk is supported between magnet poles so it can be rotated, as shown in the sketch. What happens in the disk as it rotates?

11. Does the strength of the magnet in the previous sketch have any effect on the amount of force needed to turn the disk?

12. A coin spinning on the end of a thread is lowered into a magnetic field. Explain what happens and why it does happen.

13. An aluminum cup is hung upside down on a pivot over a rotating magnet, as shown in the sketch below. Explain what happens to the cup.

Electromagnetic Induction

18–1 MOVING COILS—STATIONARY FIELDS

A simple way of demonstrating the induction process is shown in Figure 18–1. A piece of copper wire is connected to the terminals of a sensitive meter and moved

downward through a magnetic field, the wire cutting across the lines of force. While the wire is moving, a voltage, or emf, is produced, tending to drive electrons from A toward B. This emf induced by the movement of the wire across the field produces a current if a complete circuit exists. When the magnet and wire are kept stationary, no emf is produced; motion is necessary. A strong horseshoe magnet (preferably Alnico) should be used. The meter can be a millivoltmeter, milliammeter, microammeter, or galvanometer, preferably a zero-center type.

When the wire is moved upward through the magnetic field, Figure 18–2, the meter needle is deflected in the direction opposite to its previous motion. This change shows

that the induced emf and induced current have been reversed in direction. If the wire is repeatedly pumped up and down, the pointer on the meter will fluctuate from left to right, indicating the generation of alternating current (AC).

When the wire is moved endwise through the field, as from A to B and back again, no emf is produced. If the wire is moved in a direction parallel to the lines of force, as from S toward N or N toward S, no induced emf is generated. The wire has to move so that it cuts across the lines of magnetic force. This cutting is a quick way of describing the motion that must occur if any voltage is to be produced. (No one need be concerned about any damage to these imaginary lines during the cutting process, for the field is just as strong after the wire has passed through as it was before.)

The induction process is greatly enhanced if the wire is shaped into a coil. Remember, to generate a useful voltage, we can move a coil through a magnetic field.

18–2 MOVING FIELDS—STATIONARY COILS

Up to this point, we have discussed generation of voltage by moving wire so that it cuts across a magnetic field. Actually, it is often just as practical to produce emf by moving the magnetic field so that it cuts across stationary wires.

An emf is produced in a stationary coil, as illustrated in Figure 18–3, when a bar magnet is withdrawn from, or inserted into, the coil so that the lines of force, moving with the magnet, cut across the wires of the coil.

The results of this experiment can be changed by using various magnets of different strength, and/or coils that differ in their number of turns. The results then demonstrate that a greater voltage output can be obtained by using a stronger magnet and/or coils with more turns.

Furthermore, the experiment reveals that the amount of voltage output depends on the speed at which the magnet is moved. The faster the motion, the more emf is produced.

These results can be summarized as follows:

The amount of emf induced is proportional to the product of three factors that deter- mine the rate of cutting magnetic flux, namely:

• The number of lines of force

• The number of turns of the wire

• The speed of the motion of wires through field or field through wires

When lines of force are cut by wire coil, the relationship of voltage measurements to magnetic field measurements is this:

To produce 1 volt, the wire must cut 100,000,000 lines of flux per second.

Recalling that 100,000,000 lines of flux are called a weber, we can state that

Cutting 1 weber/second results in the generation of 1 volt.

For instance, when 50,000 lines of force are cut by a coil of 2,000 turns in 1 second, the total cutting is 50,000 3 2,000 5 100,000,000 lines per second, and 1 volt is induced.

EXAMPLE 18–1

Given: 300,000 lines of flux cut by a coil of 5,000 turns in 2 seconds.

Find: The value of the induced emf.

Solution

The total number of lines cut in 2 seconds is equal to

All generators operate on this principle of cutting flux lines with the relative motion of magnetic fields and coils of wire. Remember, cutting 100,000,000 lines of flux per second generates 1 volt.

18–3 FLEMING’S LEFT-HAND RULE FOR GENERATORS

The relation of direction of motion of the wire in a field to direction of induced emf can be determined by Fleming’s left-hand rule. With the thumb, forefinger, and middle finger of the left hand each placed at right angles to the other two fingers, as shown in Figure 18–4, the f orefinger (or f irst finger) gives the direction of the f ield, the thumb gives the direction of motion of the wire, and the center finger gives the direction of the induced current. This rule does not explain anything; it is merely one of the ways of determining one of these directions when the other two are known.

One way of remembering this rule is to associate the first letters of the fingers used with the first letters of the indicated quantity.

THumb stands for THrust Forefinger stands for Flux Center finger stands for Current

If you think you understand this concept well, look back at Figures 18–1 and 18–2. Look carefully at all the arrowheads indicating the various directions of field, current, and conductor motion to see if you can verify the correctness of the information presented in these drawings.

Now let us apply this left-hand rule to find the direction of current flow in the coil of Figure 18–5 when the magnet is withdrawn from the coil.

Figure 18–5 shows the withdrawal of the magnet from the coil. The magnetic field of the N pole is moving to the right, cutting across the wires of the coil. To determine the direction of induced emf using the left-hand rule, remember that the rule is based on the relative motion of the wire. Pulling the magnet to the right is equivalent to moving the coil of wire to the left. To use the left-hand rule, the thumb must point to the left, representing the relative motion of the wire through the field.

To find the direction of emf over the top of the coil, the thumb points to the left, the forefinger (for field) upward, and the center finger then gives the current direction toward the observer at the top of the coil. At the bottom of the coil, the thumb still points to the left, the field is downward, and the center finger points away from the observer, giving the current direction around the coil as shown by the arrows on the wire in Figure 18–5.

Electromagnetic Induction

18–1 MOVING COILS—STATIONARY FIELDS

A simple way of demonstrating the induction process is shown in Figure 18–1. A piece of copper wire is connected to the terminals of a sensitive meter and moved

downward through a magnetic field, the wire cutting across the lines of force. While the wire is moving, a voltage, or emf, is produced, tending to drive electrons from A toward B. This emf induced by the movement of the wire across the field produces a current if a complete circuit exists. When the magnet and wire are kept stationary, no emf is produced; motion is necessary. A strong horseshoe magnet (preferably Alnico) should be used. The meter can be a millivoltmeter, milliammeter, microammeter, or galvanometer, preferably a zero-center type.

When the wire is moved upward through the magnetic field, Figure 18–2, the meter needle is deflected in the direction opposite to its previous motion. This change shows

that the induced emf and induced current have been reversed in direction. If the wire is repeatedly pumped up and down, the pointer on the meter will fluctuate from left to right, indicating the generation of alternating current (AC).

When the wire is moved endwise through the field, as from A to B and back again, no emf is produced. If the wire is moved in a direction parallel to the lines of force, as from S toward N or N toward S, no induced emf is generated. The wire has to move so that it cuts across the lines of magnetic force. This cutting is a quick way of describing the motion that must occur if any voltage is to be produced. (No one need be concerned about any damage to these imaginary lines during the cutting process, for the field is just as strong after the wire has passed through as it was before.)

The induction process is greatly enhanced if the wire is shaped into a coil. Remember, to generate a useful voltage, we can move a coil through a magnetic field.

18–2 MOVING FIELDS—STATIONARY COILS

Up to this point, we have discussed generation of voltage by moving wire so that it cuts across a magnetic field. Actually, it is often just as practical to produce emf by moving the magnetic field so that it cuts across stationary wires.

An emf is produced in a stationary coil, as illustrated in Figure 18–3, when a bar magnet is withdrawn from, or inserted into, the coil so that the lines of force, moving with the magnet, cut across the wires of the coil.

The results of this experiment can be changed by using various magnets of different strength, and/or coils that differ in their number of turns. The results then demonstrate that a greater voltage output can be obtained by using a stronger magnet and/or coils with more turns.

Furthermore, the experiment reveals that the amount of voltage output depends on the speed at which the magnet is moved. The faster the motion, the more emf is produced.

These results can be summarized as follows:

The amount of emf induced is proportional to the product of three factors that deter- mine the rate of cutting magnetic flux, namely:

• The number of lines of force

• The number of turns of the wire

• The speed of the motion of wires through field or field through wires

When lines of force are cut by wire coil, the relationship of voltage measurements to magnetic field measurements is this:

To produce 1 volt, the wire must cut 100,000,000 lines of flux per second.

Recalling that 100,000,000 lines of flux are called a weber, we can state that

Cutting 1 weber/second results in the generation of 1 volt.

For instance, when 50,000 lines of force are cut by a coil of 2,000 turns in 1 second, the total cutting is 50,000 3 2,000 5 100,000,000 lines per second, and 1 volt is induced.

EXAMPLE 18–1

Given: 300,000 lines of flux cut by a coil of 5,000 turns in 2 seconds.

Find: The value of the induced emf.

Solution

The total number of lines cut in 2 seconds is equal to

All generators operate on this principle of cutting flux lines with the relative motion of magnetic fields and coils of wire. Remember, cutting 100,000,000 lines of flux per second generates 1 volt.

18–3 FLEMING’S LEFT-HAND RULE FOR GENERATORS

The relation of direction of motion of the wire in a field to direction of induced emf can be determined by Fleming’s left-hand rule. With the thumb, forefinger, and middle finger of the left hand each placed at right angles to the other two fingers, as shown in Figure 18–4, the f orefinger (or f irst finger) gives the direction of the f ield, the thumb gives the direction of motion of the wire, and the center finger gives the direction of the induced current. This rule does not explain anything; it is merely one of the ways of determining one of these directions when the other two are known.

One way of remembering this rule is to associate the first letters of the fingers used with the first letters of the indicated quantity.

THumb stands for THrust Forefinger stands for Flux Center finger stands for Current

If you think you understand this concept well, look back at Figures 18–1 and 18–2. Look carefully at all the arrowheads indicating the various directions of field, current, and conductor motion to see if you can verify the correctness of the information presented in these drawings.

Now let us apply this left-hand rule to find the direction of current flow in the coil of Figure 18–5 when the magnet is withdrawn from the coil.

Figure 18–5 shows the withdrawal of the magnet from the coil. The magnetic field of the N pole is moving to the right, cutting across the wires of the coil. To determine the direction of induced emf using the left-hand rule, remember that the rule is based on the relative motion of the wire. Pulling the magnet to the right is equivalent to moving the coil of wire to the left. To use the left-hand rule, the thumb must point to the left, representing the relative motion of the wire through the field.

To find the direction of emf over the top of the coil, the thumb points to the left, the forefinger (for field) upward, and the center finger then gives the current direction toward the observer at the top of the coil. At the bottom of the coil, the thumb still points to the left, the field is downward, and the center finger points away from the observer, giving the current direction around the coil as shown by the arrows on the wire in Figure 18–5.

17–9 CLAMP-ON METERS

All the instruments discussed so far in this chapter operate on magnetic principles. Be aware, though, that modern technology provides meters that employ principles of electronics and induction. Induction, as you will learn in the following chapter, involves transfer of energy from one conductor onto another without physical contact. This energy transfer occurs via the magnetic field that surrounds a current-carrying conductor. This phenomenon allows the technician to measure electrical current in a conductor without

having to break the circuit or otherwise interrupt the service. The instrument used in this manner is called a clamp-on meter, or just clamp meter, also sometimes referred to as an amp clamp; see Figure 17–19. Such instruments have a tapered jaw that can be opened and closed single-handedly by pressure action on a side lever. The jaws are clamped around the conductor in which the current is to be measured.

Although these instruments are primarily used to measure current, they can also be used to obtain voltage readings, in both AC and DC installations. The meter scale is built right into the handheld body of the instrument and can be of either analog or digital design.

Some manufacturers also offer clamp-on accessories that can be attached to a VOM or DMM, thereby providing greater versatility to an existing meter. Figure 17–20 shows how a handheld VOM looks before and after being outfitted with a clamp-on accessory.

17–10 DIGITAL MULTIMETERS

Digital multimeters, such as the one shown in Figure 17–21, have become increasingly popular in the past few years. The most apparent difference between digital meters and analog meters is the fact that digital meters display their reading in discrete digits instead

of with a pointer and scale. Some digital meters have a range switch (similar to the one used with analog meters) that sets the full-range value of the meter. Many digital meters have voltage range settings from 200 millivolts to 2,000 volts. The lower ranges are used for accuracy. For example, assume it is necessary to measure a voltage of 16 volts. The meter will be able to make a more accurate measurement when set on the 20 volts range than it will when set on the 2,000 volts range.

Digital meters that do not contain a range-setting control are known as auto-rang- ing meters. They contain a function control switch that permits selection of the electrical quantity to be measured—such as AC volts, DC volts, ohms, etc. When the meter probes are connected to the object to be tested, the meter automatically selects the proper range and displays the value.

Analog meters change scale value by inserting or removing resistance from the meter circuit. The typical resistance of an analog meter is 20,000 ohms per volt for DC and 5,000 ohms per volts for AC. This means that if the meter is set for a full-scale value of 60 volts, there will be 1.2 megohms of resistance connected in series with the meter if it is being used to measure DC (60 3 20,000 5 1,200,000) and 300 kilohms if is it is being used to measure AC (60 3 5,000 5 300,000). The impedance of the meter is of little concern if it is used to measure circuits connected to a high current source. For example, assume the voltage of a 480-volt panel is to be measured with a multimeter with a resistance of 5,000 ohms per volt. If the meter is set on the 600 volts range, the resistance connected in series with the meter is 3 megohms (600 3 5,000 5 3,000,000). This will permit a current of 160 microamperes to flow in the meter circuit (480/3,000,000 5 0.000160), which would not be enough to affect the circuit being tested.

Now assume that this meter is to be used to test a 24-volt circuit with a current flow of 100 microamperes. If the 60 volts range is used, the meter circuit contains a resistance of 300 kilohms (60 3 5,000 5 300,000). This means that a current of 80 microamperes will flow when the meter is connected to the circuit (24/300,000 5 0.000080). The con- nection of the meter to the circuit has changed the entire circuit operation. This is known as the loading effect.

Digital meters do not have this problem. Most digital meters have an input imped- ance of about 10 megohms on all ranges. This is accomplished by using field effect transistors (FETs) and a voltage divider circuit. A simple schematic for this circuit is shown in Figure 17–22. Notice that the meter input is connected across 10 megohms of resistance regardless of the range setting of the meter. If this meter is used to measure the voltage of the 24-volt circuit, a current of 2.4 microamperes will flow through the meter. This is not enough current to upset the rest of the circuit, so voltage measurements can be made accurately.

Digital Ohmmeters

Digital ohmmeters display the resistance in figures instead of using a meter movement. When using a digital ohmmeter, be sure to notice the scale indication on the meter. For example, most digital meters will display a “k” on the scale to indicate kilohms or an “M” to indicate megohms (recall that kilo means 1,000 and mega means 1,000,000). If the meter is showing a resistance of 0.200 k, it means 0.200 3 1,000, or 200 ohms. If the meter indicates 1.65 M, it means 1.65 3 1,000,000, or 1,650,000 ohms.

Appearance is not the only difference between analog and digital ohmmeters. Their operating principle is also different. Analog ohmmeters operate by measuring the amount of current change in the circuit when an unknown value of resistance is added. Digital ohmmeters measure resistance by measuring the amount of voltage drop across an un- known resistance. In the circuit shown in Figure 17–23, a constant current generator is used to supply a known amount of current to a resistor, RX. Let us assume that the amount of current supplied is 1 milliampere. The voltage dropped across the resistor is proportional to the resistance of the resistor and the amount of current flow. For example, assume the value of the unknown resistor is 4,700 ohms. The voltmeter would indicate a drop of

volts when 1 milliampere of current flows through the resistor.

The scale factor of the ohmmeter can be changed by changing the amount of current flow through the resistor. Digital ohmmeters generally exhibit an accuracy of about 61%.

The ohmmeter must never be connected to a circuit when the power is turned on.

Since the ohmmeter uses its own internal power supply, it has a very low operating voltage. If a meter is connected to power when it is set in the ohms position, it will probably be damaged or destroyed.

Low-Impedance Voltage Tester

Another device used to test voltage is simply referred to as a voltage tester. This device does measure voltage, but it does not contain a meter movement or digi- tal display. Rather, it contains a coil and a plunger. The coil produces a magnetic field, which is proportional to the voltage the tester is connected to. The higher the voltage the tester is connected to, the stronger the magnetic field becomes. The plunger must overcome the force of a spring as it is drawn into the coil, as shown in Figure 17–24, and acts as a pointer to indicate the amount of voltage the tester is connected to. The tester has an impedance of approximately 5,000 ohms and can generally be used to measure voltages as high as 600 volts. This type of tester has a very large current draw when compared to other types of voltmeters and should never be used to test low-power circuits.

The relatively high current draw of the voltage tester can be an advantage when testing certain types of circuits, however, because the tester is not susceptible to giving the misleading voltage readings caused by high-impedance ground paths or feedback voltages. An example is shown in Figure 17–25. A transformer is used to supply power to a load. Notice that neither the output side of the transformer nor the load is connected to ground. If a high-impedance voltmeter is used to measure between one side of the transformer and a grounded point, it will most likely indicate some amount of voltage. This is due to the fact that ground can act as a large capacitor and permit a small amount of current to flow through the circuit created by the meter. This high-impedance ground path can support only a few microamperes of current flow, but it is enough to operate the meter. If a voltage tester is used to make the same measurement, it will not show a voltage because there cannot be enough current flow to attract the plunger. A voltage tester is shown in Figure 17–26.

SUMMARY

• A DC galvanometer consists of a small coil of wire and a pointer connected in an assembly, moved by magnetic action in the field of a permanent magnet; small spiral hairsprings return the pointer back to the 0 mark on the meter scale.

• Galvanometers are also known as d’Arsonval meters or permanent magnet meter movements.

• An ammeter is a low-resistance meter and consists of a galvanometer and a shunt resistor of low value in parallel with the galvanometer.

• An ammeter is connected in series with the device in which current is to be measured.

• A voltmeter is a high-resistance meter and consists of a galvanometer plus a resistor in series with the galvanometer.

• A voltmeter can be connected directly to a voltage source and must be connected across (in parallel with) the device in which voltage is to be measured.

• An ohmmeter consists of a galvanometer, dry cells, and series resistors. It measures the resistance between the test leads and the instrument. An ohmmeter must be used in a dead circuit; this instrument must NOT be used on resistors that have current in them from some other source.

• A wattmeter contains a voltage coil across the line and a current coil in series with the line. A wattmeter will indicate either DC or AC watts.

• There are more electrons on the negative terminal of a device (such as a meter, resistor, or battery) than there are on its positive terminal. (Remember this point when you must determine either the polarity of a device or the electron current direction. Electrons move from the negative toward the positive terminal.)

• Electrical measurements are based on the accuracy of mathematical formulas and the reliability of precision instruments.

• Wheatstone bridges are laboratory-type, precision instruments for the measurement of unknown resistors.

• Wheatstone bridges operate on the principle that the voltage drops in a series circuit must equal the applied voltage.

• Clamp-on meters permit current readings without interrupting the circuit.

• Digital voltmeters generally maintain the same input resistance regardless of the range setting.

• Some digital meters are auto-ranging.

• Digital ohmmeters measure resistance by measuring the voltage drop across an un- known resistor when a known amount of current flows through it.

• Low-impedance voltage testers contain a coil and a plunger rather than a meter movement or digital display.

• Low-impedance voltage testers do not give misleading voltage readings caused by high- impedance ground paths or feedback voltages, an advantage when testing certain circuits.

Achievement Review

1. State the purpose of each of the following: the hairsprings in a galvanometer, a shunt in an ammeter, and a series resistor in a voltmeter.

2. Under what conditions is each of the following devices used: a Wheatstone bridge, a megohmmeter?

3. Diagram the internal circuit of a voltmeter, an ammeter, an ohmmeter, and a wattmeter.

4. The user of an ohmmeter finds that when the test leads are shorted, the adjustment does not cause the pointer to move to the 0 mark. Instead, the pointer stops at about R 5 5. Why?

5. Calculate the resistance of the shunt required to convert a 100-microampere meter with a 40-ohm moving coil to a 10-milliampere meter.

6. Calculate the series resistor required to convert the 100-microampere meter in question 5 to a voltmeter with a full scale of 100 millivolts.

7. Calculate the series resistor required to convert the 100-microampere meter in question 5 to a voltmeter scaled to 100 volts.

8. A pair of #28 AWG copper wires in a telephone cable is accidentally short- circuited. A Wheatstone bridge is connected to the accessible ends of the wires. The values for the resistances are as follows: R1 5 100 Ω, R2 5 327.8 Ω, R3 5 100 Ω. Using the formula R1 RX 5 R2 R3, calculate the distance from the accessible end of the cable to the point where the pair of wires is shorted. (The ambient temperature is 70°F.)

9. a. Using the data from the illustration in Figure 17–7, calculate the voltage across the moving coil and the voltage across the shunt when 2 amperes pass through the meter (use terminals 2 and – ).

b. Using the 10 and – terminals, find the voltage across the moving coil and the voltage across the shunt when 10 amperes pass through the meter.

10. Two resistors, A and B, are connected in parallel. This combination is placed in series with a third resistor, C. This entire group is connected across a 120-volt DC supply. The resistance of A is 20 ohms. The current in B is 3 amperes, and the current in C is 5 amperes.

a. Determine the voltage across A, the resistance of B, and the resistance of C.

b. If resistor A is accidentally open-circuited, find the new voltages across resistor A and resistor C.

11. A 0- to 150-volt voltmeter has a resistance of 2,000 ohms per volt. It is de- sired to change this voltmeter to a 0- to 600-volt instrument by the addition of an external multiplier. What is the resistance, in ohms, of this external multiplier?

12. A 0- to 150-volt DC voltmeter has a resistance of 100 ohms per volt.

a. What is the instrument resistance?

b. What is the instrument full-scale current?

c. Extend the range of the voltmeter to 750 volts by adding an external multi- plier. What is the resistance of this external multiplier?

d. What is the power dissipation of the external multiplier when the voltmeter is used to measure 750 volts?

13. A d’Arsonval movement has a full-scale deflection at 25 milliamperes, and the coil has a resistance of 2 ohms.

a. What is the resistance of the multiplier required to convert this instrument into a voltmeter with a full-scale deflection at 300 volts?

b. What is the resistance of the shunt required to convert this instrument into an ammeter with a full-scale deflection at 25 amperes?

14. The power to a 25-watt lamp is being measured with a voltmeter and an am- meter. The voltmeter has a resistance of 14,160 ohms. The meter is connected directly across the lamp terminals. When the ammeter reads 0.206 ampere, the voltmeter reads 119 volts.

a. What is the true power taken by the lamp?

b. What percentage of error is introduced if the instrument power is neglected?

15. A DC instrument has a resistance of 2.5 ohms. It gives a full-scale deflection when carrying 20 milliamperes.

a. What is the resistance of the shunt required to give the instrument a full-scale deflection when the current is 10 amperes?

b. What resistance is connected in series with the instrument movement so that a full-scale deflection occurs when the instrument is connected across 150 volts?

16. The resistance of a 0- to 50-millivoltmeter is 10 ohms. This meter is connected with an external shunt in a circuit in which the current is 100 amperes.

a. Draw a diagram showing the method of connecting the instrument and the shunt in the circuit.

b. What instrument current causes full-scale deflection?

c. Determine the resistance of the shunt that is used with the instrument to cause a full-scale deflection.

17. Why are electronic wattmeters replacing dynamic wattmeters?

18. Digital meters that do not contain a control to set the range for measuring volt- age, current, or resistance are known as meters.

19. Most digital voltmeters exhibit an input resistance of about 10 MΩ on all ranges.

How is this accomplished?

20. Explain the difference in operating principle between analog ohmmeters and digital ohmmeters.

17–9 CLAMP-ON METERS

All the instruments discussed so far in this chapter operate on magnetic principles. Be aware, though, that modern technology provides meters that employ principles of electronics and induction. Induction, as you will learn in the following chapter, involves transfer of energy from one conductor onto another without physical contact. This energy transfer occurs via the magnetic field that surrounds a current-carrying conductor. This phenomenon allows the technician to measure electrical current in a conductor without

having to break the circuit or otherwise interrupt the service. The instrument used in this manner is called a clamp-on meter, or just clamp meter, also sometimes referred to as an amp clamp; see Figure 17–19. Such instruments have a tapered jaw that can be opened and closed single-handedly by pressure action on a side lever. The jaws are clamped around the conductor in which the current is to be measured.

Although these instruments are primarily used to measure current, they can also be used to obtain voltage readings, in both AC and DC installations. The meter scale is built right into the handheld body of the instrument and can be of either analog or digital design.

Some manufacturers also offer clamp-on accessories that can be attached to a VOM or DMM, thereby providing greater versatility to an existing meter. Figure 17–20 shows how a handheld VOM looks before and after being outfitted with a clamp-on accessory.

17–10 DIGITAL MULTIMETERS

Digital multimeters, such as the one shown in Figure 17–21, have become increasingly popular in the past few years. The most apparent difference between digital meters and analog meters is the fact that digital meters display their reading in discrete digits instead

of with a pointer and scale. Some digital meters have a range switch (similar to the one used with analog meters) that sets the full-range value of the meter. Many digital meters have voltage range settings from 200 millivolts to 2,000 volts. The lower ranges are used for accuracy. For example, assume it is necessary to measure a voltage of 16 volts. The meter will be able to make a more accurate measurement when set on the 20 volts range than it will when set on the 2,000 volts range.

Digital meters that do not contain a range-setting control are known as auto-rang- ing meters. They contain a function control switch that permits selection of the electrical quantity to be measured—such as AC volts, DC volts, ohms, etc. When the meter probes are connected to the object to be tested, the meter automatically selects the proper range and displays the value.

Analog meters change scale value by inserting or removing resistance from the meter circuit. The typical resistance of an analog meter is 20,000 ohms per volt for DC and 5,000 ohms per volts for AC. This means that if the meter is set for a full-scale value of 60 volts, there will be 1.2 megohms of resistance connected in series with the meter if it is being used to measure DC (60 3 20,000 5 1,200,000) and 300 kilohms if is it is being used to measure AC (60 3 5,000 5 300,000). The impedance of the meter is of little concern if it is used to measure circuits connected to a high current source. For example, assume the voltage of a 480-volt panel is to be measured with a multimeter with a resistance of 5,000 ohms per volt. If the meter is set on the 600 volts range, the resistance connected in series with the meter is 3 megohms (600 3 5,000 5 3,000,000). This will permit a current of 160 microamperes to flow in the meter circuit (480/3,000,000 5 0.000160), which would not be enough to affect the circuit being tested.

Now assume that this meter is to be used to test a 24-volt circuit with a current flow of 100 microamperes. If the 60 volts range is used, the meter circuit contains a resistance of 300 kilohms (60 3 5,000 5 300,000). This means that a current of 80 microamperes will flow when the meter is connected to the circuit (24/300,000 5 0.000080). The con- nection of the meter to the circuit has changed the entire circuit operation. This is known as the loading effect.

Digital meters do not have this problem. Most digital meters have an input imped- ance of about 10 megohms on all ranges. This is accomplished by using field effect transistors (FETs) and a voltage divider circuit. A simple schematic for this circuit is shown in Figure 17–22. Notice that the meter input is connected across 10 megohms of resistance regardless of the range setting of the meter. If this meter is used to measure the voltage of the 24-volt circuit, a current of 2.4 microamperes will flow through the meter. This is not enough current to upset the rest of the circuit, so voltage measurements can be made accurately.

Digital Ohmmeters

Digital ohmmeters display the resistance in figures instead of using a meter movement. When using a digital ohmmeter, be sure to notice the scale indication on the meter. For example, most digital meters will display a “k” on the scale to indicate kilohms or an “M” to indicate megohms (recall that kilo means 1,000 and mega means 1,000,000). If the meter is showing a resistance of 0.200 k, it means 0.200 3 1,000, or 200 ohms. If the meter indicates 1.65 M, it means 1.65 3 1,000,000, or 1,650,000 ohms.

Appearance is not the only difference between analog and digital ohmmeters. Their operating principle is also different. Analog ohmmeters operate by measuring the amount of current change in the circuit when an unknown value of resistance is added. Digital ohmmeters measure resistance by measuring the amount of voltage drop across an un- known resistance. In the circuit shown in Figure 17–23, a constant current generator is used to supply a known amount of current to a resistor, RX. Let us assume that the amount of current supplied is 1 milliampere. The voltage dropped across the resistor is proportional to the resistance of the resistor and the amount of current flow. For example, assume the value of the unknown resistor is 4,700 ohms. The voltmeter would indicate a drop of

volts when 1 milliampere of current flows through the resistor.

The scale factor of the ohmmeter can be changed by changing the amount of current flow through the resistor. Digital ohmmeters generally exhibit an accuracy of about 61%.

The ohmmeter must never be connected to a circuit when the power is turned on.

Since the ohmmeter uses its own internal power supply, it has a very low operating voltage. If a meter is connected to power when it is set in the ohms position, it will probably be damaged or destroyed.

Low-Impedance Voltage Tester

Another device used to test voltage is simply referred to as a voltage tester. This device does measure voltage, but it does not contain a meter movement or digi- tal display. Rather, it contains a coil and a plunger. The coil produces a magnetic field, which is proportional to the voltage the tester is connected to. The higher the voltage the tester is connected to, the stronger the magnetic field becomes. The plunger must overcome the force of a spring as it is drawn into the coil, as shown in Figure 17–24, and acts as a pointer to indicate the amount of voltage the tester is connected to. The tester has an impedance of approximately 5,000 ohms and can generally be used to measure voltages as high as 600 volts. This type of tester has a very large current draw when compared to other types of voltmeters and should never be used to test low-power circuits.

The relatively high current draw of the voltage tester can be an advantage when testing certain types of circuits, however, because the tester is not susceptible to giving the misleading voltage readings caused by high-impedance ground paths or feedback voltages. An example is shown in Figure 17–25. A transformer is used to supply power to a load. Notice that neither the output side of the transformer nor the load is connected to ground. If a high-impedance voltmeter is used to measure between one side of the transformer and a grounded point, it will most likely indicate some amount of voltage. This is due to the fact that ground can act as a large capacitor and permit a small amount of current to flow through the circuit created by the meter. This high-impedance ground path can support only a few microamperes of current flow, but it is enough to operate the meter. If a voltage tester is used to make the same measurement, it will not show a voltage because there cannot be enough current flow to attract the plunger. A voltage tester is shown in Figure 17–26.

SUMMARY

• A DC galvanometer consists of a small coil of wire and a pointer connected in an assembly, moved by magnetic action in the field of a permanent magnet; small spiral hairsprings return the pointer back to the 0 mark on the meter scale.

• Galvanometers are also known as d’Arsonval meters or permanent magnet meter movements.

• An ammeter is a low-resistance meter and consists of a galvanometer and a shunt resistor of low value in parallel with the galvanometer.

• An ammeter is connected in series with the device in which current is to be measured.

• A voltmeter is a high-resistance meter and consists of a galvanometer plus a resistor in series with the galvanometer.

• A voltmeter can be connected directly to a voltage source and must be connected across (in parallel with) the device in which voltage is to be measured.

• An ohmmeter consists of a galvanometer, dry cells, and series resistors. It measures the resistance between the test leads and the instrument. An ohmmeter must be used in a dead circuit; this instrument must NOT be used on resistors that have current in them from some other source.

• A wattmeter contains a voltage coil across the line and a current coil in series with the line. A wattmeter will indicate either DC or AC watts.

• There are more electrons on the negative terminal of a device (such as a meter, resistor, or battery) than there are on its positive terminal. (Remember this point when you must determine either the polarity of a device or the electron current direction. Electrons move from the negative toward the positive terminal.)

• Electrical measurements are based on the accuracy of mathematical formulas and the reliability of precision instruments.

• Wheatstone bridges are laboratory-type, precision instruments for the measurement of unknown resistors.

• Wheatstone bridges operate on the principle that the voltage drops in a series circuit must equal the applied voltage.

• Clamp-on meters permit current readings without interrupting the circuit.

• Digital voltmeters generally maintain the same input resistance regardless of the range setting.

• Some digital meters are auto-ranging.

• Digital ohmmeters measure resistance by measuring the voltage drop across an un- known resistor when a known amount of current flows through it.

• Low-impedance voltage testers contain a coil and a plunger rather than a meter movement or digital display.

• Low-impedance voltage testers do not give misleading voltage readings caused by high- impedance ground paths or feedback voltages, an advantage when testing certain circuits.

Achievement Review

1. State the purpose of each of the following: the hairsprings in a galvanometer, a shunt in an ammeter, and a series resistor in a voltmeter.

2. Under what conditions is each of the following devices used: a Wheatstone bridge, a megohmmeter?

3. Diagram the internal circuit of a voltmeter, an ammeter, an ohmmeter, and a wattmeter.

4. The user of an ohmmeter finds that when the test leads are shorted, the adjustment does not cause the pointer to move to the 0 mark. Instead, the pointer stops at about R 5 5. Why?

5. Calculate the resistance of the shunt required to convert a 100-microampere meter with a 40-ohm moving coil to a 10-milliampere meter.

6. Calculate the series resistor required to convert the 100-microampere meter in question 5 to a voltmeter with a full scale of 100 millivolts.

7. Calculate the series resistor required to convert the 100-microampere meter in question 5 to a voltmeter scaled to 100 volts.

8. A pair of #28 AWG copper wires in a telephone cable is accidentally short- circuited. A Wheatstone bridge is connected to the accessible ends of the wires. The values for the resistances are as follows: R1 5 100 Ω, R2 5 327.8 Ω, R3 5 100 Ω. Using the formula R1 RX 5 R2 R3, calculate the distance from the accessible end of the cable to the point where the pair of wires is shorted. (The ambient temperature is 70°F.)

9. a. Using the data from the illustration in Figure 17–7, calculate the voltage across the moving coil and the voltage across the shunt when 2 amperes pass through the meter (use terminals 2 and – ).

b. Using the 10 and – terminals, find the voltage across the moving coil and the voltage across the shunt when 10 amperes pass through the meter.

10. Two resistors, A and B, are connected in parallel. This combination is placed in series with a third resistor, C. This entire group is connected across a 120-volt DC supply. The resistance of A is 20 ohms. The current in B is 3 amperes, and the current in C is 5 amperes.

a. Determine the voltage across A, the resistance of B, and the resistance of C.

b. If resistor A is accidentally open-circuited, find the new voltages across resistor A and resistor C.

11. A 0- to 150-volt voltmeter has a resistance of 2,000 ohms per volt. It is de- sired to change this voltmeter to a 0- to 600-volt instrument by the addition of an external multiplier. What is the resistance, in ohms, of this external multiplier?

12. A 0- to 150-volt DC voltmeter has a resistance of 100 ohms per volt.

a. What is the instrument resistance?

b. What is the instrument full-scale current?

c. Extend the range of the voltmeter to 750 volts by adding an external multi- plier. What is the resistance of this external multiplier?

d. What is the power dissipation of the external multiplier when the voltmeter is used to measure 750 volts?

13. A d’Arsonval movement has a full-scale deflection at 25 milliamperes, and the coil has a resistance of 2 ohms.

a. What is the resistance of the multiplier required to convert this instrument into a voltmeter with a full-scale deflection at 300 volts?

b. What is the resistance of the shunt required to convert this instrument into an ammeter with a full-scale deflection at 25 amperes?

14. The power to a 25-watt lamp is being measured with a voltmeter and an am- meter. The voltmeter has a resistance of 14,160 ohms. The meter is connected directly across the lamp terminals. When the ammeter reads 0.206 ampere, the voltmeter reads 119 volts.

a. What is the true power taken by the lamp?

b. What percentage of error is introduced if the instrument power is neglected?

15. A DC instrument has a resistance of 2.5 ohms. It gives a full-scale deflection when carrying 20 milliamperes.

a. What is the resistance of the shunt required to give the instrument a full-scale deflection when the current is 10 amperes?

b. What resistance is connected in series with the instrument movement so that a full-scale deflection occurs when the instrument is connected across 150 volts?

16. The resistance of a 0- to 50-millivoltmeter is 10 ohms. This meter is connected with an external shunt in a circuit in which the current is 100 amperes.

a. Draw a diagram showing the method of connecting the instrument and the shunt in the circuit.

b. What instrument current causes full-scale deflection?

c. Determine the resistance of the shunt that is used with the instrument to cause a full-scale deflection.

17. Why are electronic wattmeters replacing dynamic wattmeters?

18. Digital meters that do not contain a control to set the range for measuring volt- age, current, or resistance are known as meters.

19. Most digital voltmeters exhibit an input resistance of about 10 MΩ on all ranges.

How is this accomplished?

20. Explain the difference in operating principle between analog ohmmeters and digital ohmmeters.

17–6 MEGOHMMETERS

An instrument called a megohmmeter is used for insulation testing and similar high-resistance tests. The megohmmeter contains a high-voltage generator that supplies current through the series resistors and the unknown resistance (R) to the two-coil assembly that operates the pointer; see Figure 17–13.

Note in the figure that permanent magnets supply the field for the DC generator and the field for the moving coil assembly. The potential coil is connected in series with R2 across the generator output. The current coil is connected in series with the unknown resistance. The current in the coil depends on the value of the unknown resistance. The potential coil and the current coil are fastened together and can rotate only as a single unit.

Since there is no spring in the coil and pointer assembly, the pointer can take any position on the scale when the meter is not in use. If there is no external connection across the ground and line terminals, when the generator is operated the current in the potential coil causes a magnetic force that rotates the coil assembly counterclockwise, moving the pointer to the infinity (∞) end of the scale (open-circuit point). If the ground and line terminals are shorted (if the unknown R has a value of 0 ohms), there is almost no current in the potential coil. Thus, the strong field of the current coil will rotate the assembly clockwise and move the pointer to the 0 end of the scale.

When the value of the unknown R is neither very high nor very low, the currents in the two coils produce opposing torques. As a result, the coil and pointer assembly comes to rest at the position near the middle, where these torques balance each other. A low value of external resistance permits the current coil to turn the pointer assembly closer to the 0 end of the scale. As the assembly is moved closer to the 0 side, the potential coil is pushed far enough into the north-pole field to prevent further turning. In the presence of

a high external resistance, the current coil has less effect and the potential coil moves the pointer closer to the ∞ end of the scale. The scale is marked to show external resistance in megohms.

In addition to the megohmmeter, various electronic instruments operated from a 120-volt AC line can measure high resistance.

17–7 WATTMETERS

As stated in Chapter 9, Watts 5 Volts 3 Amperes in DC circuits. To measure the wattage of a circuit, a meter must have two coils; one coil is affected by the voltage and one by the current. The voltage coil is the moving coil and is connected across the current line so that the magnetic strength of the coil is proportional to the line voltage. The combination of the moving coil and its series resistor in Figure 17–14 is similar to a voltmeter, described previously. However, instead of having a permanent magnet to provide the magnetic field for the moving coil, the wattmeter has current coils to provide the magnetic field. The magnetic strength of these coils is proportional to the current through them (the current supplied to the device being tested).

The amount of movement of the coil and pointer depends on the strength of both coils. If there is a voltage but no current, then there is no magnetic field to turn the moving coil; therefore, the pointer reads 0. If the magnetic strength of either coil is

increased, the turning force increases; that is, the turning force depends on the product of the magnetic strengths of the two coils, just as the force between any two magnets depends on the product of their magnetic strengths (Chapter 16).

With this coil arrangement, the pointer reading depends on the product of the volt- age on one coil and the current in the other coil. Thus, the meter scale is calibrated in watts. The coils used have air cores, not iron cores. A wattmeter can operate on AC as well as DC, because the magnetic polarity of both coils reverses when the current reverses, and the turning force remains in the same direction.

Wattmeters are more necessary for AC measurements than for DC measurements. In DC circuits, watts are always equal to volts 3 amperes, and wattmeters are not required. In AC circuits, there are occasions when watts are not equal to volts 3 amperes, and wattmeters are needed to indicate the power consumption in the circuit.

Many wattmeters have terminals marked “V” for the voltmeter function and “A” for the ammeter function. Such meters are connected as shown in Figure 17–15. Note that in this case one of the “V” terminals always connects to one of the “A” terminals. Therefore, many instruments provide a common terminal only, which is generally labeled 6 or COM2. Figure 17–16 illustrates how the hookup looks with such instruments.

Wattmeters that contain both stationary and moving coils are generally referred to as dynamic wattmeters. Dynamic wattmeters are rapidly being replaced with electronic wattmeters due to the high cost of constructing a dynamic wattmeter. Electronic wattmeters contain an electronic circuit that permits the use of a standard d’Arsonval movement or can be output to a digital display.

17–8 BRIDGE CIRCUITS

One of the most common methods used to accurately measure values of resistance, inductance, and capacitance is with a bridge constructed by connecting four components together to form a parallel-series circuit. All four components are of the same type, such as four resistors, four inductors, or four capacitors. The bridge used to measure resistance is called a Wheatstone bridge. The basic circuit for a Wheatstone bridge is shown in Figure 17–17. The bridge operates on the principle that the sum of the voltage drops in a series circuit must equal the applied voltage. A galvanometer is used to measure the voltage between points B and D. The galvanometer can be connected to different values of resistance or directly between points B and D. Values of resistance are used to change the sensitivity of the meter circuit. When the meter is connected directly across the two points, its sensitivity is maximum.

In Figure 17–17, assume the battery has a voltage of 12 volts, and that resistors R1 and R2 are precision resistors and have the same value of resistance. Since resistors R1 and R2 are connected in series and have the same value, each will have a voltage drop equal to one-half of the applied voltage, or 6 volts. This means that point B is 6 volts more negative than point A and 6 volts more positive than point C.

Resistors RV (variable) and RX (unknown) in Figure 17–17 are connected in series with each other. Resistor RX represents the unknown value of resistance to be measured.

Resistor RV can be adjusted for different resistive values. If the value of RV is greater than the value of RX, the voltage at point D will be more positive than the voltage at point B. This will cause the pointer of the zero-center galvanometer to move in one direction. If the value of RV is less than RX, the voltage at point D will be more negative than the voltage at point B, causing the pointer to move in the opposite direction. When the value of RV becomes equal to RX, the voltage at point D will become equal to the voltage at point B. When this occurs, the galvanometer will indicate 0. A Wheatstone bridge is shown in Figure 17–18.