science universe

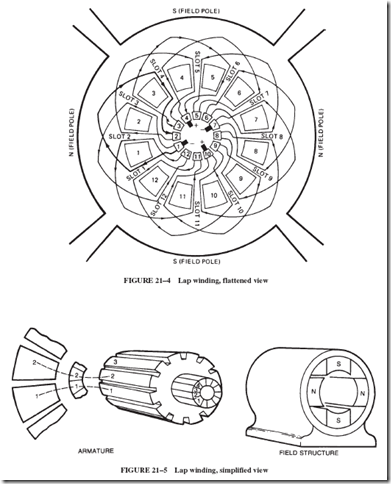
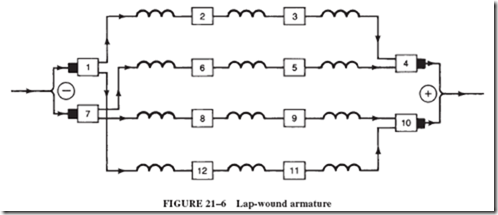
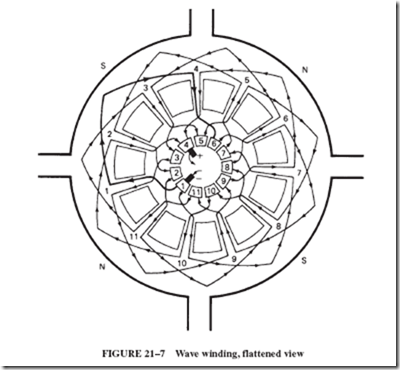
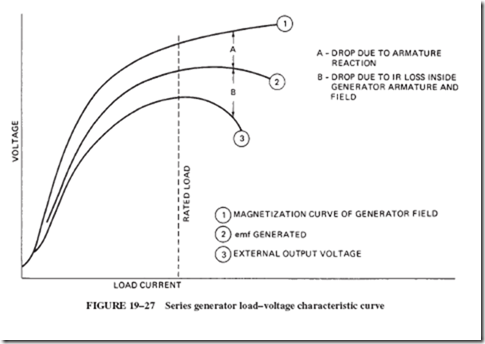
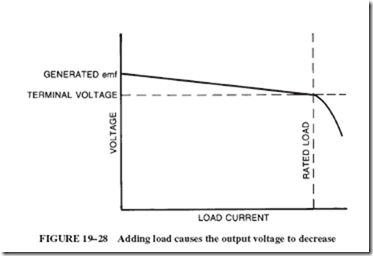
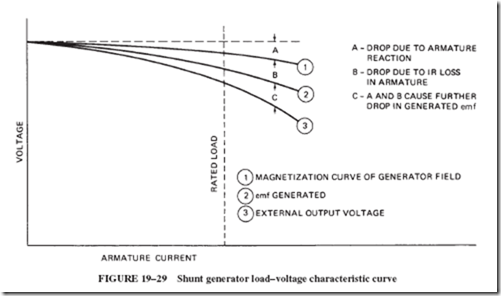
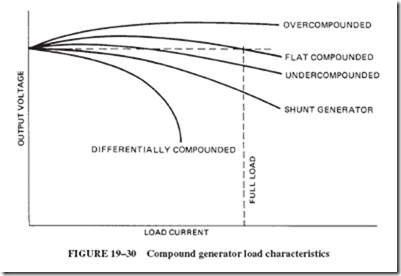
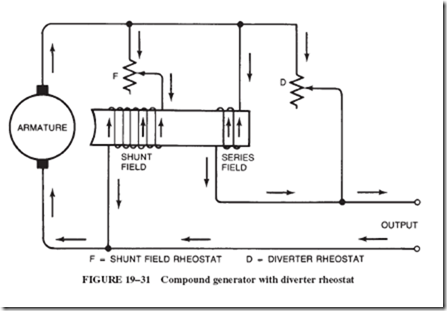
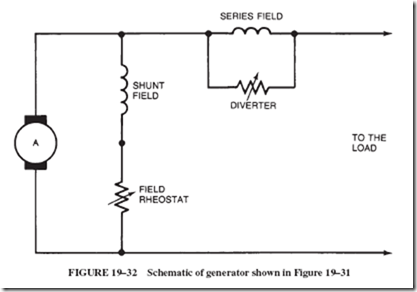
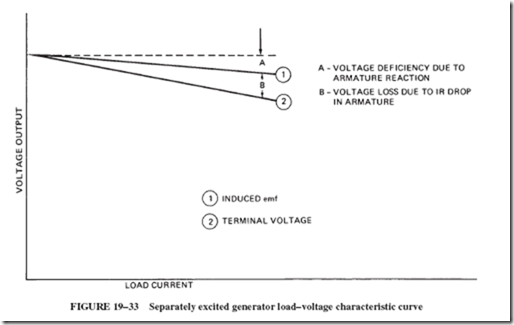
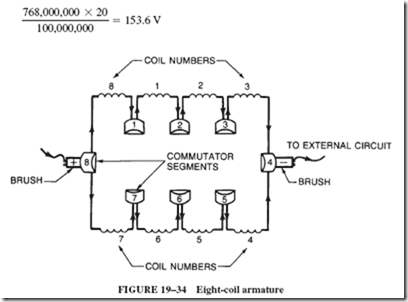
21–4 FIELD DISTORTION AND THE NEED FOR INTERPOLES

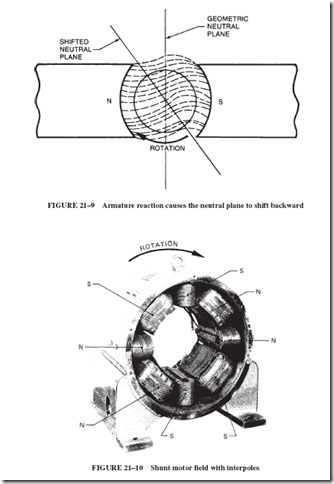
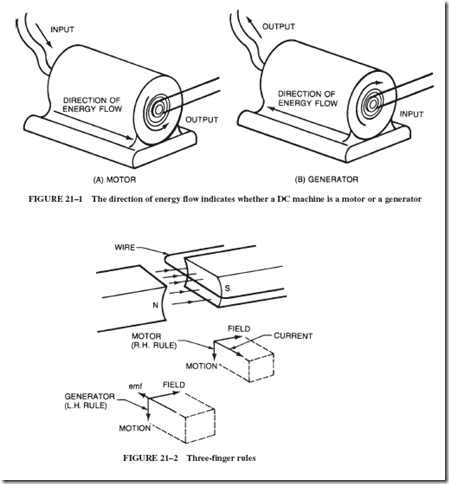
In our study of generators we learned of a concept known as armature reaction (Section 19–4), which results in a distortion of the magnetic field. This distortion causes the neutral plane to shift forward (with respect to the direction of rotation).

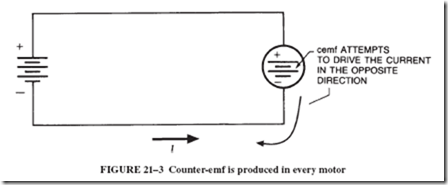
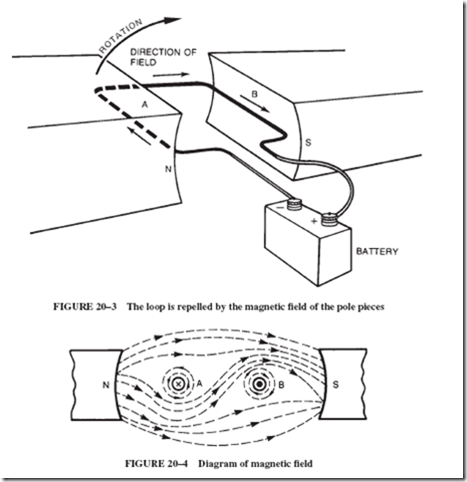
In electric motors, as in generators, the current of the armature produces a magnetic field that interacts with and distorts the magnetic field in which the armature rotates. However, the magnetic action of motors is opposite to that of generators and, consequently, the neutral plane is shifted backward with respect to the direction of rotation; see Figure 21–9.

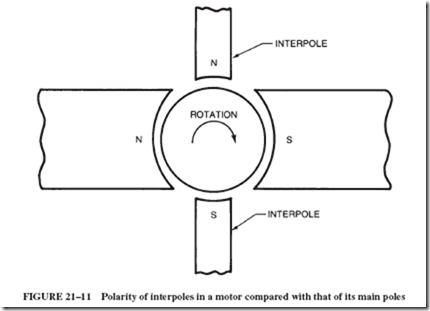
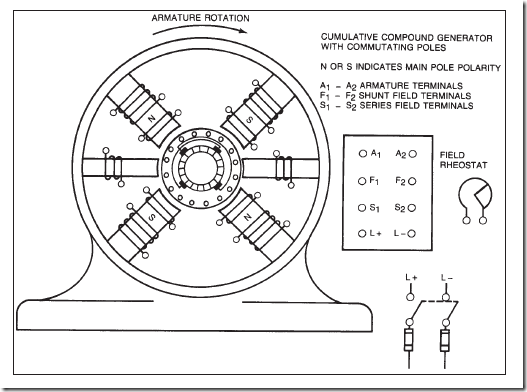
To counteract this warping of the magnetic field, large DC motors are often built with interpoles, or commutating poles. The windings of these poles are in series with the armature. The poles produce a field that counteracts the armature field. Interpoles increase efficiency and control excessive sparking at the commutator when the motor is operated under conditions requiring high armature current. In the motor shown in Figure 21–10, the four large poles are the main field poles, and the four small ones are the interpoles.

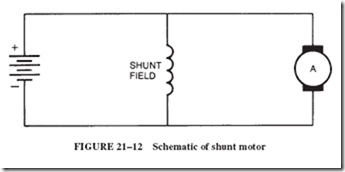
In a motor, the interpoles must have the same polarity as the main poles directly in back of them (back in the sense of direction of rotation of the armature); see Figure 21–11. In a generator, the interpoles have the same polarity as the main poles directly ahead of them.

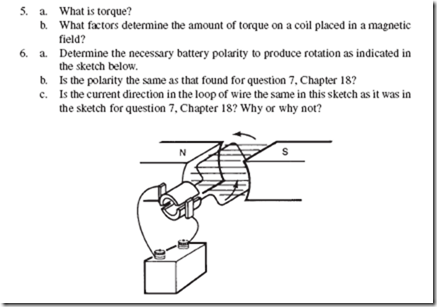
In Figure 21–10, assuming a clockwise rotation of the armature (not shown), the polarities of the four main field poles and their interpoles would be as indicated.

DC machines are generally designed in such a manner that they can be employed as either a generator or a motor. Since the polarity of the interpoles differs between a genera- tor and a motor, many manufacturers provide access to the interpole winding by bringing leads out to the terminal connection box. Interpole, or commutating field, leads are generally labeled C1 and C2. Since the commutating field is connected in series with the armature, some manufacturers label the leads S3 and S4.

21–5 THE SHUNT MOTOR

DC motors, like DC generators, are classified by the way their field coils are connected; thus, we differentiate between shunt motors, series motors, and compound motors.

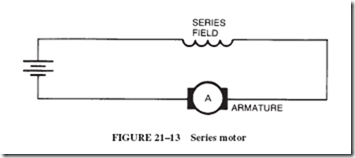
Shunt motors, as their name implies, have their field coils connected in parallel to their armature and the power supply, as shown in Figure 21–12. The shunt field, therefore, consists of many turns of fine wire and maintains a steady magnetic field as long as the line voltage is constant. The torque of the motor is therefore solely a function of the armature current.

Let us assume that the load on a motor is increased. As a result, the motor slows down. Consequently, the cemf goes down also, the armature current increases, and the motor increases its torque to meet the new demand of the load.

This action can be summarized by a form of shorthand notation, in which arrows pointing up indicate an increase of the quantity and vice versa, like this:

Speed Regulation

When the torque increases to meet the new load demand, the speed will readjust itself; thus, the motor maintains a fairly constant speed. We say that the motor is self-regulating. This self-regulating effect, called speed regulation, is a characteristic of the motor itself. The speed regulation is numerically expressed as

Note: The concept of speed regulation is not just for shunt motors but applies to all types of electric motors. The lower the percentage of regulation, the more constant the speed of the motor.

In a DC motor, the speed regulation is proportional to the resistance of the armature. The lower the armature resistance, the better speed regulation the motor will exhibit. DC motors operate on the principle of attraction and repulsion of magnetism between the magnetic field developed in the pole pieces and the magnetic field developed in the armature. If load is added to the motor, the motor must produce more torque to overcome the added load. To produce more torque, the magnetic field strength of the armature or pole pieces must increase. The increase in field strength is accomplished when the armature speed decreases, causing less counter-emf to be produced in the armature. The decrease of cemf permits more current to flow through the armature, causing an increase in magnetic field strength. The amount of counter-emf produced in the armature is proportional to the magnetic field strength of the pole pieces and the speed of armature rotation. If the armature resistance is very low, a small decrease of cemf will cause a significant increase in current and magnetic field strength.

EXAMPLE 21–3

Given: A motor turns 1,620 rpm at rated load but speeds up to 1,750 rpm when the load is removed.

Find: The speed regulation.

Solution

The concept of regulation allows us to compare the speed change characteristic of various motors. A low-percentage regulation indicates a fairly constant speed. Example 21–3 is typical of shunt motors, which makes this type of motor desirable for industrial applications with constant speed requirements.

Shunt motors have a peculiar characteristic. When resistance is added to their shunt field circuits, thereby decreasing the current and the magnetic flux, the motors will speed up. (This feature is explained in greater detail later in this chapter.) This fact must be understood to appreciate that shunt motors, especially the large ones, must be protected against an accidental loss of their magnetic field. If, for some reason, the shunt field should open up, the loss of the magnetic field would cause the motor to accelerate to dangerously high levels.

If you wonder how a motor can run without a magnetic field, remember that there is a sufficient amount of residual magnetism to cause the motor to run away. Runaway motors can eventually destroy themselves due to the physical stress caused by centrifugal force.

Note: Study groups desiring a more detailed analysis of shunt-motor characteristics are referred to the Appendix.

21–6 THE SERIES MOTOR

Unlike the shunt-motor field in which magnetization is attained by a small current in many turns, the series-motor field carries the entire current in a low-resistance coil of few turns; see Figure 21–13. Shunt field magnetization remains constant whether or not armature current changes; series field magnetization changes as the motor changes under varying load.

Unlike the shunt motor, the series motor does not have a constant speed characteristic. With every change in load, the current through the field coil changes correspondingly, causing tremendous speed variations.

Unlike in the shunt motor, the torque and speed of the series motor are inversely proportional. In our accepted shorthand notation, this can be expressed as

In other words, whenever the load on a series motor is reduced, the motor will speed up. In fact, if the load should be completely disconnected, the series motor might run away and destroy itself.

One might reason that the brisk acceleration would cause the cemf to increase rap- idly enough to shut off the torque-producing current. This, however, is not possible due to the sharp decrease in the magnetic flux. Thus, the torque accelerates the motor further, theoretically without limit. With the load removed, speeds can easily rise to 10,000 rpm, and if the friction in the motor is less than equivalent to the torque produced, speeds build up even more.

In actuality, the top speed of series motors is limited.

• In small motors, friction from bearings, brushes, and windage limits the speed. At 10,000 rpm, the entire power input can be expended on friction, and there is no further increase in speed.

• In large motors, high speed produces inertial forces that burst the bands holding the armature coils in place. At 5,000 rpm, the surface of an 8-inch-diameter armature is traveling at about 2 miles per minute, and each ounce of copper wire in the slots requires a force of 180 pounds to hold it in place.

For these reasons, it is recommended that series motors be used only in applications where the load is geared directly to the shaft of the motor. Belt drives, which are prone to slip or break, are not suitable for use with series motors.

A motor with such severe limitations must have some other strong advantages to recommend itself, and, indeed, it does. The series motor has the ability to provide high levels of torque at startup or whenever a sudden overload condition places a heavy demand on the motor. Let us see why this is so.

Torque is an interaction of the two fields produced by the armature and the series field. Let us assume the current through the motor is doubled. This, in turn, doubles the magnetic flux of the series field as well as the magnetic flux of the armature. As a result, the torque will increase by a factor of (2)2, or 4. We say that the torque of the series motor is proportional to the square of the current. (Of course, this statement is made with the assumption that the magnetic core is not saturated. Nevertheless, it should make the point that the series motor is ideally suited for any industrial application where extremely high torque is required and where very heavy overload is suddenly applied during operation. Examples of such applications include cranes, hoists, electric loco- motives for railways, and other electrical vehicles.)

But remember that this type of motor cannot be used where a relatively constant speed is required from no load to full load. Because the series motor has poor speed regulation, it can reach a dangerously fast speed when the load is removed.

Note: Study groups desiring a more detailed analysis of series-motor characteristics are referred to the Appendix.

21–7 THE COMPOUND MOTOR

Compare the advantages of series and shunt motors. The shunt motor has a more constant speed, but the series motor (of the same power rating) can exert a much greater torque without a great increase in current. These two desirable features can be obtained in the same motor by placing both a series field winding and a shunt field winding on the field poles of the motor, which is now a compound motor.

Consider the effect of adding a few series field turns to an existing shunt motor. At heavy loads, when the motor slows down, the increased current through the series field boosts the field strength, which gives added torque and speed.

Or consider the effect of adding a shunt field to a series motor. At light loads, when the motor tends to overspeed because of decreased field flux, the added constant-flux shunt field provides enough flux to put a reasonable limit on the top speed.

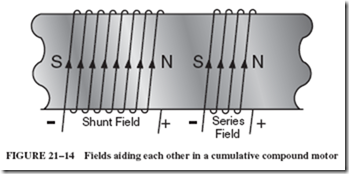
Combining the two fields within one motor results in a machine that retains the excellent starting torque of the series motor without the excessive speedup when the load is removed. These beneficial characteristics are derived only when the two field coils, the shunt and the series coils, produce magnetic fields aligned in the same direction (Figure 21–14). Wound in this manner, the windings are aiding each other in producing flux, and the motor is called a cumulative compound motor; see Figure 21–14. Most compound motors are wound in this manner and, therefore, the term compound motor implies that it is cumulatively compounded.

Infrequently, a motor is connected with its series field opposing the shunt field; in other words, their magnetic fields are opposing each other. This can be done either by winding the two coils in different directions on the field pole, as shown in Figure 21–15, or simply by reversing the current through one set of coils, arranged as in Figure 21–14. This type of motor is said to be differentially compounded.

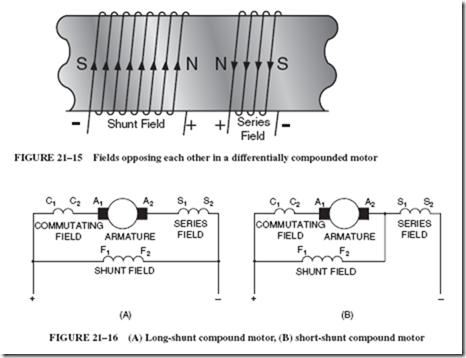
When the shunt field is connected directly to the line, the connection is called long shunt, as shown in Figure 21–16A. When the shunt field is connected directly across the armature, the connection is called short shunt; see Figure 21–16B. The long-shunt connection is generally used, but the type of connection makes no particular difference in motor performace.

If a given long-shunt motor is reconnected to a short shunt, slight changes do occur. At no load, with small armature current, the shunt field current passing through

the series field slightly increases the total field flux. As a result, the maximum rpm of the motor is reduced. At heavy overload with high armature current, the voltage drop on the series field reduces voltage and current available to the shunt field. As a result, to maintain a high torque, the motor can take 1% more current and run 1% faster than when connected long shunt.

Excellent speed regulation can be obtained with this type of motor. The motor runs with practically constant speed under varying load conditions.

In summary, compound motors are generally connected long shunt and cumulative compound. Such motors develop a high torque when the load is suddenly increased. This motor also has another advantage: It does not race to an excessively high speed if the load is removed.

Some of the industrial applications for this motor are drives for passenger and freight elevators, for metal stamping presses, for rolling mills in the steel industry, for metal shears, and in similar applications.

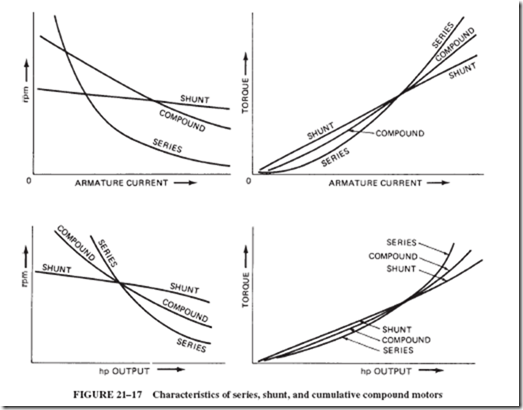
The graphs in Figure 21–17 compare the characteristics of the three types of motors: series, shunt, and cumulative compound. Compound motors can be built with characteristics approaching either the series or the shunt characteristics, depending on the relative division of ampere-turns between series and shunt coils.

DC Motors

21–1 DC MACHINES—MOTOR OR GENERATOR?

The brief introduction to motors provided by Chapter 20 points to great similarities between motors and generators. Certainly their physical design features are so similar that often it is impossible, without close inspection, to tell a motor from a generator. In fact, there are a few machines that can be used either as a motor or as a generator.

All electrical machines are essentially energy converters. It is the direction of the energy flow through the machine that determines its name and function. Figure 21–1 illustrates this idea.

Both machines are look-alikes with their armature, field poles, commutators, and such. Where they differ is in the opposite application of electromagnetism. This fact is

emphasized by the contrast between Fleming’s left-hand rule for generators versus the right-hand rule for motors. If you compare Figure 20–6 with Figure 18–4, you may notice that for any two quantities that are the same, the third one is exactly the opposite. The same idea is conveyed by Figure 21–2. This fact has some significant consequences, as we shall see in the following section.

21–2 THE COUNTER-emf IN A MOTOR

When a coil of wire is rotated within a magnetic field, it generates an emf, regardless of what causes its motion. It does not necessarily take an external agent sup- plying muscle energy to the crank on a shaft, as implied by Figure 21–1B. It can be electromagnetic motor action that sets the armature spinning and starts to generate an emf. In other words, every motor inadvertently acts like a generator and produces a volt- age within itself while it is running. This voltage is known as counter-emf (cemf ), because its polarity is such that it opposes the applied line voltage; see Figure 21–3.

Like the output voltage from a generator, the amount of cemf depends on two factors:

1. The strength of the magnetic field

2. The speed of rotation

We can, in fact, use the generator formula, first introduced in Section 19–8, to calculate the cemf generated within the motor.

EXAMPLE 21–1

It may surprise some students to see that the cemf is nearly as high as the applied voltage. In fact, it is sometimes difficult for a beginner to realize the value of the emf that a motor generates. The generated emf is a measure of the useful mechanical energy obtained from the electrons passing through the armature.

As stated before, this emf is called counter-emf or back-emf because it opposes the voltage applied to the motor. This is a useful sort of opposition. The generated back-emf opposes the movement of the incoming electrons in the same way that the weight of a sack of groceries opposes the efforts of a boy carrying the sack up a flight of stairs. If there is no opposition, no useful work is done. If the boy leaves the groceries on the sidewalk, he can run upstairs faster, but the groceries are not delivered. An electric heater element generates no back-emf; the electrons can run through it rapidly, but they produce no mechanical work.

It is easy to make an adjustment on the electric motor so that it generates no counter-emf. Merely bolt down the armature so that it cannot turn. Then electrons run through the motor faster and more easily, and the motor is converted into an electric heater.

The example we used before had a line voltage of 120 volts applied. This power line has two jobs to do: First, it must supply 100 volts, which is converted to mechanical energy. Second, it must supply enough additional voltage to force the 10-ampere current through the 2-ohm wire resistance. It takes 20 volts to put 10 amperes through 2 ohms; thus, the line voltage must be 100 + 20 = 120 volts.

Carry this calculation one step further. Multiply the total applied voltage (120 volts) by the current (10 amperes) and find the total power input, 1,200 watts.

Generated voltage (100 volts) times 10 amperes equals the useful mechanical power output, 1,000 watts. This same figure was found once before: the 1.34 horsepower output that was found from torque and rpm (Chapter 20).

The power input is 1,200 watts; the output is 1,000 watts. Where did the other 200 watts go? By multiplying the 20 volts used on resistance by the 10 amperes, we get 200 watts. This represents the rate at which energy is converted into heat in the armature. The rate of heat production is 200 watts.

The counter-emf does not produce useful mechanical energy, but the useful power produced can be calculated from the counter-emf and the current. This is just like saying that the useful power (working rate) accomplished by the grocery bagger can be calculated from the weight of the sack and the speed with which he lifts it. The weight is not doing the work; but the greater the weight, the more work done by the bagger.

EXAMPLE 21–2

Given: A 5-ohm armature taking 6 amperes from a 115-volt line when operating at its normal rating.

Find:

a. Counter-emf generated

b. Power input

c. Useful power output

d. Heating rate

e. Efficiency

f. Current and heating rate if the motor is stalled

Solution

21–3 ARMATURE WINDINGS

As pointed out in Section 19–2, two main types of drum armature windings are in use: the lap winding and the wave winding. In Figure 21–4 (as in Figure 19–14), the innermost circle of numbered rectangles represents an end view of commutator bars. The next circle of 12 distorted rectangles represents sections of the face of the armature. (A different view of the face sections is shown in Figure 21–5.)

Outside of the rectangles in Figure 21–4, representing the cylindrical armature face, are lines showing the coil connections at the back of the armature. (This information is not visible in a diagram such as Figure 21–5.) The field poles represent a four-pole field in which this armature is to rotate. (Note the simplified view of the field structure in Figure 21–5.)

The Lap Winding

A few minutes spent in tracing the wiring in Figure 21–4 makes the pattern seem less complicated, since the 12 coils on this armature are all alike. Start with the negative

brush touching bar 1. Electrons flowing from the DC supply line to bar 1 can escape into the winding by either of two paths. (The brushes are shown as if inside, rather than in their actual position outside.)

Follow the heavily shaded wire through slot 1 and back through slot 4. The main feature of the lap winding is that the finish end of this coil, coming through slot 4, is connected to commutator bar 2, next to the one from which we started (1). From bar 2 the current path is through slot 2, back by slot 5 to bar 3. Then the current path goes out slot 3 and back by slot 6 to bar 4. Bar 4 is in contact with a positive brush that completes the circuit to the DC power source. Returning again to bar 1, another path can be traced through slots 3, 12, 2, 11, 1, and 10, back to the other positive brush.

Note that under both N poles, the current is away from the commutator. Under both S poles, the current is toward the commutator. With the help of Figure 21–5 and the three-finger right-hand rule, determine the direction of rotation of the armature.

Figure 21–6 is a schematic view of the circuits through this four-pole armature. Each numbered rectangle corresponds to a numbered commutator bar, as shown in Figure 21–4. The purpose of this sketch is to show that there are four parallel paths through this armature.

There are so many variations in armature windings that the subject can merely be in- troduced in these few pages; for the whole story, consult a text dealing only with armatures.

In general, lap windings require

• As many brushes as there are poles

• As many parallel paths through the armature as there are poles

The Wave Winding

Figure 21–7 shows another pattern called the wave winding. Compare it with the lap winding. Notice that the wave winding accomplishes a similar control of current direction in the wires under each field pole, so that rotation is produced. (One need not be concerned because the wires in slot 7 carry currents in opposite directions, which oppose and therefore cancel each other. Because slot 7 is between field poles at the instant shown, there is no force on the wires anyway.)

To see the difference between wave winding, Figure 21–7, and lap winding, Figure 21–6, observe the heavily shaded wire that starts from bar 1. The ends of the coil are spread apart, connecting to widely separated bars in wave winding rather than to adjacent bars as in lap winding.

Eleven bars and slots, rather than 12, are used in wave winding, because a 4-pole wave winding does not fit on a 12-bar, 12-slot armature. The reason for this difference, as well as the reasons for the locations of the commutator connections, involves calculations not worked out here.

Trace through or (better yet) redraw the winding, starting with a sketch that does not show the wiring. Begin at bar 1, through slot 1, over to slot 4, to bar 6, out slot 6, to slot 9, to bar 11, continuing around the armature until bar 4 is finally reached. There is another path from bar 1, out slot 10, in slot 7, and so forth, again finally arriving at bar 4.

Figure 21–8 shows, in schematic fashion, that there are only two parallel paths through this armature. (The numbered rectangles correspond to the commutator bars in Figure 21–7.)

Wave windings require

• A minimum of two brushes but a maximum of as many brushes as poles

• Only two parallel paths through the armature in one complete wave winding, regard- less of the number of brushes

Comparative Uses

Lap windings are good for high-current, low-voltage motors because they have more parallel paths for the current. Wave windings are good for high-voltage, low-current motors and generators because they have more coils in series.

Up to this point, we have assumed that the armature rotates in the field of a permanent magnet. Actually, until recent times, motors with permanent magnetic fields have had limited applications in industry. Although this trend is changing (see Section 21–11), most industrial motors have traditionally used, and still use, electromagnets for their field structure.

Field-magnet coils may be in series, or in parallel, or one in series and one in parallel with the armature, as in compound-wound motors, which have two sets of windings. The behavior of these magnetic field windings and their effect on motor performance is the subject of the next chapter.

DC Motors

21–1 DC MACHINES—MOTOR OR GENERATOR?

The brief introduction to motors provided by Chapter 20 points to great similarities between motors and generators. Certainly their physical design features are so similar that often it is impossible, without close inspection, to tell a motor from a generator. In fact, there are a few machines that can be used either as a motor or as a generator.

All electrical machines are essentially energy converters. It is the direction of the energy flow through the machine that determines its name and function. Figure 21–1 illustrates this idea.

Both machines are look-alikes with their armature, field poles, commutators, and such. Where they differ is in the opposite application of electromagnetism. This fact is

emphasized by the contrast between Fleming’s left-hand rule for generators versus the right-hand rule for motors. If you compare Figure 20–6 with Figure 18–4, you may notice that for any two quantities that are the same, the third one is exactly the opposite. The same idea is conveyed by Figure 21–2. This fact has some significant consequences, as we shall see in the following section.

21–2 THE COUNTER-emf IN A MOTOR

When a coil of wire is rotated within a magnetic field, it generates an emf, regardless of what causes its motion. It does not necessarily take an external agent sup- plying muscle energy to the crank on a shaft, as implied by Figure 21–1B. It can be electromagnetic motor action that sets the armature spinning and starts to generate an emf. In other words, every motor inadvertently acts like a generator and produces a volt- age within itself while it is running. This voltage is known as counter-emf (cemf ), because its polarity is such that it opposes the applied line voltage; see Figure 21–3.

Like the output voltage from a generator, the amount of cemf depends on two factors:

1. The strength of the magnetic field

2. The speed of rotation

We can, in fact, use the generator formula, first introduced in Section 19–8, to calculate the cemf generated within the motor.

EXAMPLE 21–1

It may surprise some students to see that the cemf is nearly as high as the applied voltage. In fact, it is sometimes difficult for a beginner to realize the value of the emf that a motor generates. The generated emf is a measure of the useful mechanical energy obtained from the electrons passing through the armature.

As stated before, this emf is called counter-emf or back-emf because it opposes the voltage applied to the motor. This is a useful sort of opposition. The generated back-emf opposes the movement of the incoming electrons in the same way that the weight of a sack of groceries opposes the efforts of a boy carrying the sack up a flight of stairs. If there is no opposition, no useful work is done. If the boy leaves the groceries on the sidewalk, he can run upstairs faster, but the groceries are not delivered. An electric heater element generates no back-emf; the electrons can run through it rapidly, but they produce no mechanical work.

It is easy to make an adjustment on the electric motor so that it generates no counter-emf. Merely bolt down the armature so that it cannot turn. Then electrons run through the motor faster and more easily, and the motor is converted into an electric heater.

The example we used before had a line voltage of 120 volts applied. This power line has two jobs to do: First, it must supply 100 volts, which is converted to mechanical energy. Second, it must supply enough additional voltage to force the 10-ampere current through the 2-ohm wire resistance. It takes 20 volts to put 10 amperes through 2 ohms; thus, the line voltage must be 100 + 20 = 120 volts.

Carry this calculation one step further. Multiply the total applied voltage (120 volts) by the current (10 amperes) and find the total power input, 1,200 watts.

Generated voltage (100 volts) times 10 amperes equals the useful mechanical power output, 1,000 watts. This same figure was found once before: the 1.34 horsepower output that was found from torque and rpm (Chapter 20).

The power input is 1,200 watts; the output is 1,000 watts. Where did the other 200 watts go? By multiplying the 20 volts used on resistance by the 10 amperes, we get 200 watts. This represents the rate at which energy is converted into heat in the armature. The rate of heat production is 200 watts.

The counter-emf does not produce useful mechanical energy, but the useful power produced can be calculated from the counter-emf and the current. This is just like saying that the useful power (working rate) accomplished by the grocery bagger can be calculated from the weight of the sack and the speed with which he lifts it. The weight is not doing the work; but the greater the weight, the more work done by the bagger.

EXAMPLE 21–2

Given: A 5-ohm armature taking 6 amperes from a 115-volt line when operating at its normal rating.

Find:

a. Counter-emf generated

b. Power input

c. Useful power output

d. Heating rate

e. Efficiency

f. Current and heating rate if the motor is stalled

Solution

21–3 ARMATURE WINDINGS

As pointed out in Section 19–2, two main types of drum armature windings are in use: the lap winding and the wave winding. In Figure 21–4 (as in Figure 19–14), the innermost circle of numbered rectangles represents an end view of commutator bars. The next circle of 12 distorted rectangles represents sections of the face of the armature. (A different view of the face sections is shown in Figure 21–5.)

Outside of the rectangles in Figure 21–4, representing the cylindrical armature face, are lines showing the coil connections at the back of the armature. (This information is not visible in a diagram such as Figure 21–5.) The field poles represent a four-pole field in which this armature is to rotate. (Note the simplified view of the field structure in Figure 21–5.)

The Lap Winding

A few minutes spent in tracing the wiring in Figure 21–4 makes the pattern seem less complicated, since the 12 coils on this armature are all alike. Start with the negative

brush touching bar 1. Electrons flowing from the DC supply line to bar 1 can escape into the winding by either of two paths. (The brushes are shown as if inside, rather than in their actual position outside.)

Follow the heavily shaded wire through slot 1 and back through slot 4. The main feature of the lap winding is that the finish end of this coil, coming through slot 4, is connected to commutator bar 2, next to the one from which we started (1). From bar 2 the current path is through slot 2, back by slot 5 to bar 3. Then the current path goes out slot 3 and back by slot 6 to bar 4. Bar 4 is in contact with a positive brush that completes the circuit to the DC power source. Returning again to bar 1, another path can be traced through slots 3, 12, 2, 11, 1, and 10, back to the other positive brush.

Note that under both N poles, the current is away from the commutator. Under both S poles, the current is toward the commutator. With the help of Figure 21–5 and the three-finger right-hand rule, determine the direction of rotation of the armature.

Figure 21–6 is a schematic view of the circuits through this four-pole armature. Each numbered rectangle corresponds to a numbered commutator bar, as shown in Figure 21–4. The purpose of this sketch is to show that there are four parallel paths through this armature.

There are so many variations in armature windings that the subject can merely be in- troduced in these few pages; for the whole story, consult a text dealing only with armatures.

In general, lap windings require

• As many brushes as there are poles

• As many parallel paths through the armature as there are poles

The Wave Winding

Figure 21–7 shows another pattern called the wave winding. Compare it with the lap winding. Notice that the wave winding accomplishes a similar control of current direction in the wires under each field pole, so that rotation is produced. (One need not be concerned because the wires in slot 7 carry currents in opposite directions, which oppose and therefore cancel each other. Because slot 7 is between field poles at the instant shown, there is no force on the wires anyway.)

To see the difference between wave winding, Figure 21–7, and lap winding, Figure 21–6, observe the heavily shaded wire that starts from bar 1. The ends of the coil are spread apart, connecting to widely separated bars in wave winding rather than to adjacent bars as in lap winding.

Eleven bars and slots, rather than 12, are used in wave winding, because a 4-pole wave winding does not fit on a 12-bar, 12-slot armature. The reason for this difference, as well as the reasons for the locations of the commutator connections, involves calculations not worked out here.

Trace through or (better yet) redraw the winding, starting with a sketch that does not show the wiring. Begin at bar 1, through slot 1, over to slot 4, to bar 6, out slot 6, to slot 9, to bar 11, continuing around the armature until bar 4 is finally reached. There is another path from bar 1, out slot 10, in slot 7, and so forth, again finally arriving at bar 4.

Figure 21–8 shows, in schematic fashion, that there are only two parallel paths through this armature. (The numbered rectangles correspond to the commutator bars in Figure 21–7.)

Wave windings require

• A minimum of two brushes but a maximum of as many brushes as poles

• Only two parallel paths through the armature in one complete wave winding, regard- less of the number of brushes

Comparative Uses

Lap windings are good for high-current, low-voltage motors because they have more parallel paths for the current. Wave windings are good for high-voltage, low-current motors and generators because they have more coils in series.

Up to this point, we have assumed that the armature rotates in the field of a permanent magnet. Actually, until recent times, motors with permanent magnetic fields have had limited applications in industry. Although this trend is changing (see Section 21–11), most industrial motors have traditionally used, and still use, electromagnets for their field structure.

Field-magnet coils may be in series, or in parallel, or one in series and one in parallel with the armature, as in compound-wound motors, which have two sets of windings. The behavior of these magnetic field windings and their effect on motor performance is the subject of the next chapter.

20–4 THE NEED FOR ADDED ARMATURE COILS

This impractical single-coil armature has a variety of faults, one of which is the irregularity of the torque that it produces. When the loop is horizontal, the force on the wire is at its greatest; when the loop is vertical, there is no force on the wire. This is illustrated by the graph in Figure 20–10. Note the similarity of this graph with that of Figure 19–8, which shows the voltage fluctuations of a simple generator. Other drawings in this chapter, too, will look familiar and will help convey the idea that the design and the internal functions of DC motors are very similar to those of DC generators.

A steadier torque is achieved by using the several coils of a drum-wound armature. The armature shown in Figure 20–11 is just as appropriate in a motor as it is in a generator.

Figure 20–11 shows a similar but simpler drum winding. Assume that the S pole of the field magnet is at the left. (It has been omitted from the diagram in order to show the windings clearly.) Trace incoming electrons from the negative brush through commutat or segment 1 through coil A to segment 2, then through B to segment 3, where the positive brush leads to the completed circuit (not shown) through a source of DC and back to the negative brush. From the negative brush, another circuit can be traced through armature coils C and D to the positive brush. Compare this drum winding with that shown in Figure 19–13 to note the similarity in principle.

The circuitry of this drum-wound armature is redrawn two different ways in Figure 20–12 to reveal the series-parallel arrangement of the four-loop armature. Note that with this arrangement, only one additional pair of commutator segments is needed. All four coils, receiving current from the power source simultaneously, contribute their torque to aid rotation of the armature.

In the preceding section we explained that commutation must take place at the moment a loop enters the neutral plane. In a practical DC motor, the brushes are so arranged that they will short-circuit the loop as it passes through the neutral plane. This will eliminate undesirable sparking between the brushes and the commutator.

As Figure 20–13 shows, there is no current in coil C because both ends of it touch the same brush. Similarly, there can be no current in coil B. This condition exists at the instant when coils B and C are in a vertical position. Even if there were current in coils B and C, no torque would be produced. Therefore, the absence of current in the coils during this short interval is no disadvantage. At this same instant, coils A and D are in horizontal position, where they are producing maximum torque.

20–5 FROM TORQUE TO HORSEPOWER

Some students may wonder about the significance of torque, since this term has been used so frequently in our discussion of mechanical energy.

Torque is an essential component used in the calculation of the horsepower rating of a machine. Torque by itself does not tell the power of a machine; speed must be taken into account. We can say that

Horsepower is proportional to torque and speed.

Let us see what needs to be done to determine the amount of horsepower developed by a four-coil armature such as the one shown in Figure 20–11. First we need to determine the torque exerted on the armature. This can be done two different ways: experimentally and mathematically.

Experimentally, the torque of a motor is measured directly by a device called a Prony brake, as shown in Figure 20–14. Tightening the bolts makes the brake tend to turn along with the motor pulley. The brake arm is restrained by the stationary spring scale; thus, a torque load is placed on the motor. The torque is the product of the effective length (l) of the torque arm in feet times the net force (F) on the scale in pounds.

A more sophisticated device known as an electrodynamometer can be used to measure torque. Such a device, resembling an electric motor, utilizes the interaction of magnetic forces to yield readings of torque when coupled to the shaft of a motor.

Mathematically, the torque exerted on the armature of a motor can be found by use of the following equation:

EXAMPLE 20–1

Given: An armature, 6 inches long, placed between magnetic poles as shown in Figure 20–15. The armature carries 200 turns. Flux density equals 50,000 lines per square inch. Current through the armature equals 10 amperes. The armature is designed like the one shown in Figures 20–11 and 20–12.

Find: Torque exerted by the armature.

Solution

200 turns = 400 wires = Z in the formula (every loop has two edges that cut the flux lines). Total number of flux lines to be cut 5 1,200,000 (24 x 50,000).

Calculation of Horsepower

Remember, horsepower is a function of torque and speed. Specifically,

Speed of the motor can be found with a revolutions counter and stopwatch, or a tachometer, or a calibrated stroboscopic light. Tachometers can read the rotational speed directly in revolutions per minute (rpm). Thus, the true mechanical horsepower output (or brake horsepower) can be determined from measurements of torque and speed.

EXAMPLE 20–2

Given: The armature of the preceeding example developing 5.65 pound-feet, turning at 1,250 revolutions per minute.

Find: The horsepower output.

Solution

One horsepower equals 746 watts, so 1.34 horsepower equals 1,000 watts. Assume that this armature has a current of 10 amperes. If it is 100% efficient, a power input of 100 volts 3 10 amperes 5 1,000 watts, or 1.34 horsepower.

If the horsepower output is known, from electrical data, torque can readily be calculated for any known value of rpm.

SUMMARY

• Electrons moving through a magnetic field are pushed sideways in a direction at right angles to the field and to their original direction.

• This fact explains the motion of armatures in DC and AC motors and the controlled movement of electron streams in electrical arcs or cathode-ray tubes.

• A three-finger right-hand rule is used to describe the motor effect.

• Torque is the twisting effect that produces rotation about an axis.

• The quantity of torque is needed for the computation of horsepower.

• DC motors require commutators for the reversal of current through the armature loop every 180°.

• Reversal of current must occur when the wire loop enters the neutral plane.

• The drum armature is an effective way of arranging coils to produce a continuous torque in a motor.

Achievement Review

1. In the sketch below, how should magnet poles be placed so that the wire is moved upward when the switch is closed?

2. What happens to the wire in question 1 if an alternating current (60 cycle) is sent through the wire?

3. A brass strip is fastened to the left terminal in the sketch below and rests in loose contact with the right-hand terminal. What happens when a battery is connected to the terminals

a. With the left one negative?

b. With the right one negative?

7. The center of a 6-foot-long plank is placed on a fulcrum as shown. How much torque is developed if a force of 75 pounds is applied at the end of the plank?

8. Calculate the torque produced on a lap-wound armature of 300 wires. Total armature current is 40 amperes; flux is 2,125,000 lines; m 5 2.

9. How much force does the torque in question 8 produce at the rim of a 4-inch- diameter pulley?

10. The armature in question 8 rotates at 990 revolutions per minute. Calculate the horsepower.

20–4 THE NEED FOR ADDED ARMATURE COILS

This impractical single-coil armature has a variety of faults, one of which is the irregularity of the torque that it produces. When the loop is horizontal, the force on the wire is at its greatest; when the loop is vertical, there is no force on the wire. This is illustrated by the graph in Figure 20–10. Note the similarity of this graph with that of Figure 19–8, which shows the voltage fluctuations of a simple generator. Other drawings in this chapter, too, will look familiar and will help convey the idea that the design and the internal functions of DC motors are very similar to those of DC generators.

A steadier torque is achieved by using the several coils of a drum-wound armature. The armature shown in Figure 20–11 is just as appropriate in a motor as it is in a generator.

Figure 20–11 shows a similar but simpler drum winding. Assume that the S pole of the field magnet is at the left. (It has been omitted from the diagram in order to show the windings clearly.) Trace incoming electrons from the negative brush through commutat or segment 1 through coil A to segment 2, then through B to segment 3, where the positive brush leads to the completed circuit (not shown) through a source of DC and back to the negative brush. From the negative brush, another circuit can be traced through armature coils C and D to the positive brush. Compare this drum winding with that shown in Figure 19–13 to note the similarity in principle.

The circuitry of this drum-wound armature is redrawn two different ways in Figure 20–12 to reveal the series-parallel arrangement of the four-loop armature. Note that with this arrangement, only one additional pair of commutator segments is needed. All four coils, receiving current from the power source simultaneously, contribute their torque to aid rotation of the armature.

In the preceding section we explained that commutation must take place at the moment a loop enters the neutral plane. In a practical DC motor, the brushes are so arranged that they will short-circuit the loop as it passes through the neutral plane. This will eliminate undesirable sparking between the brushes and the commutator.

As Figure 20–13 shows, there is no current in coil C because both ends of it touch the same brush. Similarly, there can be no current in coil B. This condition exists at the instant when coils B and C are in a vertical position. Even if there were current in coils B and C, no torque would be produced. Therefore, the absence of current in the coils during this short interval is no disadvantage. At this same instant, coils A and D are in horizontal position, where they are producing maximum torque.

20–5 FROM TORQUE TO HORSEPOWER

Some students may wonder about the significance of torque, since this term has been used so frequently in our discussion of mechanical energy.

Torque is an essential component used in the calculation of the horsepower rating of a machine. Torque by itself does not tell the power of a machine; speed must be taken into account. We can say that

Horsepower is proportional to torque and speed.

Let us see what needs to be done to determine the amount of horsepower developed by a four-coil armature such as the one shown in Figure 20–11. First we need to determine the torque exerted on the armature. This can be done two different ways: experimentally and mathematically.

Experimentally, the torque of a motor is measured directly by a device called a Prony brake, as shown in Figure 20–14. Tightening the bolts makes the brake tend to turn along with the motor pulley. The brake arm is restrained by the stationary spring scale; thus, a torque load is placed on the motor. The torque is the product of the effective length (l) of the torque arm in feet times the net force (F) on the scale in pounds.

A more sophisticated device known as an electrodynamometer can be used to measure torque. Such a device, resembling an electric motor, utilizes the interaction of magnetic forces to yield readings of torque when coupled to the shaft of a motor.

Mathematically, the torque exerted on the armature of a motor can be found by use of the following equation:

EXAMPLE 20–1

Given: An armature, 6 inches long, placed between magnetic poles as shown in Figure 20–15. The armature carries 200 turns. Flux density equals 50,000 lines per square inch. Current through the armature equals 10 amperes. The armature is designed like the one shown in Figures 20–11 and 20–12.

Find: Torque exerted by the armature.

Solution

200 turns = 400 wires = Z in the formula (every loop has two edges that cut the flux lines). Total number of flux lines to be cut 5 1,200,000 (24 x 50,000).

Calculation of Horsepower

Remember, horsepower is a function of torque and speed. Specifically,

Speed of the motor can be found with a revolutions counter and stopwatch, or a tachometer, or a calibrated stroboscopic light. Tachometers can read the rotational speed directly in revolutions per minute (rpm). Thus, the true mechanical horsepower output (or brake horsepower) can be determined from measurements of torque and speed.

EXAMPLE 20–2

Given: The armature of the preceeding example developing 5.65 pound-feet, turning at 1,250 revolutions per minute.

Find: The horsepower output.

Solution

One horsepower equals 746 watts, so 1.34 horsepower equals 1,000 watts. Assume that this armature has a current of 10 amperes. If it is 100% efficient, a power input of 100 volts 3 10 amperes 5 1,000 watts, or 1.34 horsepower.

If the horsepower output is known, from electrical data, torque can readily be calculated for any known value of rpm.

SUMMARY

• Electrons moving through a magnetic field are pushed sideways in a direction at right angles to the field and to their original direction.

• This fact explains the motion of armatures in DC and AC motors and the controlled movement of electron streams in electrical arcs or cathode-ray tubes.

• A three-finger right-hand rule is used to describe the motor effect.

• Torque is the twisting effect that produces rotation about an axis.

• The quantity of torque is needed for the computation of horsepower.

• DC motors require commutators for the reversal of current through the armature loop every 180°.

• Reversal of current must occur when the wire loop enters the neutral plane.

• The drum armature is an effective way of arranging coils to produce a continuous torque in a motor.

Achievement Review

1. In the sketch below, how should magnet poles be placed so that the wire is moved upward when the switch is closed?

2. What happens to the wire in question 1 if an alternating current (60 cycle) is sent through the wire?

3. A brass strip is fastened to the left terminal in the sketch below and rests in loose contact with the right-hand terminal. What happens when a battery is connected to the terminals

a. With the left one negative?

b. With the right one negative?

7. The center of a 6-foot-long plank is placed on a fulcrum as shown. How much torque is developed if a force of 75 pounds is applied at the end of the plank?

8. Calculate the torque produced on a lap-wound armature of 300 wires. Total armature current is 40 amperes; flux is 2,125,000 lines; m 5 2.

9. How much force does the torque in question 8 produce at the rim of a 4-inch- diameter pulley?

10. The armature in question 8 rotates at 990 revolutions per minute. Calculate the horsepower.

Mechanical Motion from Electrical Energy

20–1 BASIC MOTOR ACTION

The term motor action was described briefly in Section 16–4. The sketch accompanying this explanation is reproduced for your convenience as Figure 20–1.

Figure 20–1 illustrates that a wire carrying electrons across a magnetic field will be pushed sideways. The current in the wire has a magnetic field of its own. The wire’s magnetic field combines with the externally applied magnetic field. The result of these combined fields causes the closely bunched, distorted lines of force to push the wire into the area that is less densely occupied by flux lines. This same idea is demonstrated, in a slightly different manner, by the sketch in Figure 20–2.

To apply this effect in an electric motor, examine the effect of an external magnetic field on a rectangular loop of wire. Assume that the wire is supplied with DC from a battery and that the external magnetic field is supplied by a permanent magnet, Figure 20–3. The sections of the loop that lie parallel to the field are not affected by the field. The side

of the loop marked A is pushed upward; the side marked B is pushed downward. Let us see why this happens.

Figure 20–4 represents a vertical cross-sectional view of the loop in the magnetic field shown in Figure 20–3. The heavy circles represent wires A and B in Figure 20–3. The X in the A circle represents electrons moving away from the observer (like the tail of an arrow flying away). The dot in the B circle represents electrons moving toward the observer (the point of an approaching arrow). The circular patterns around A and B represent the magnetic field of the current in these wires. (Using the left-hand rule, check the correctness of the direction arrows.)

Underneath A, the N S S magnetic field combines with the field of the wire, making a strong field under the wire. Above A, the field of the magnet and the field of the wire are in opposite directions. They cancel each other, making the weak field represented by the less-concentrated lines above A. Wire A is lifted by the strong magnetic field beneath. To account for this lifting effect, think of the N S S lines of force as both repelling each other and attempting to straighten themselves. A similar effect at B pushes wire B downward, much as a round stick is pushed down by a string, as shown in Figure 20–5.

The direction of motion of the wire can be found quickly by using a three-finger right-hand rule: With first finger, middle finger, and thumb at right angles to each other, forefinger 5 f ield, center finger 5 current, thumb 5 motion; see Figure 20–6.

Notice the similarity with Fleming’s left-hand rule for generators, as described in Section 18–3. The two rules may appear identical to the casual observer, but note the important difference:

The left-hand rule is used with generators, and the right-hand rule applies to motors.

This statement is, of course, based on the theory that defines current flow as a motion of electrons from negative to positive.

20–2 TORQUE AND ROTARY MOTION

Torque, also known as a moment of force, is a measure of the twisting effect that produces rotation about an axis. Torque is measured in pound-feet (or in similar units) and is calculated by multiplying the applied force by the radius of the turning circle.

Figure 20–7 shows examples of torque. Figure 20–7A represents a wagon wheel with a 4-foot diameter and the weight of a person (150 pounds) pressing downward on one of the spokes. Applying what we know about calculating torque,

2 ft x 150 lb = 300 lb-ft of torque

Note: Remember, radius is one-half the diameter.

Figure 20–7B shows two hands on a steering wheel with an 8-inch radius applying 5 pounds of pressure. Thus,

2⁄3 x 5 lb = 31⁄3 lb-ft of torque

The torque delivered by a motor is a more useful quantity than the single force pushing against the two vertical sides of the coil. The torque of an electric motor is

actually caused by the interaction of two magnetic fields, namely the main magnetic field (in our examples provided by the permanent magnet) and the magnetism created by the current flowing through the armature. Torque is a necessary quantity in the calculation of a motor’s horsepower, but we will discuss more about that later.

A Word of Caution:

Many students mistakenly confuse the term torque with work because of its similarity of calculation, the result being the mathematical product of force 3 distance.

Torque and work are not the same thing, and can exist independently of one another. To differentiate between the two terms, it is customary to call the unit of work the foot-pound and the unit of torque the pound-foot.

The lifting of one side of the loop and the pushing down of the other side creates a turning effect, or torque, on the loop of the wire. This combination of forces is the

torque that turns the armature of electric motors. This same method also explains the turning effect on the moving coil in a voltmeter or ammeter.

20–3 THE NEED FOR COMMUTATION

Imagine that the loop has rotated clockwise 90° from the position shown in Figure 20–3, until wires A and B are vertically aligned, as shown in Figure 20–8. Continued lifting of wire A and pushing down on wire B are useless. The loop is now perpendicular to the magnetic field and is said to be in the neutral plane.

When the loop is in the neutral plane, no torque is produced. To achieve continued rotation, the current direction in the loop must be reversed just as the loop enters the neutral plane. Since the loop is in motion, its inertia will carry it past the neutral plane position and, thus, continued rotation is assured.

This necessary reversal of the current is accomplished, for a single coil, by a two-segment commutator; see Figure 20–9. At the instant shown, electrons flow from the negative brush through A and return to the positive brush through B. As A is lifted to

the top of its rotation, the commutator segment that supplied electrons to A slides away from the negative brush and touches the positive brush; thus, the current in the loop is reversed. Momentum carries the loop past the vertical position. A is then pushed downward to the right, B is lifted to the left, and another half-turn of rotation continues. This description may help explain the need for commutators to reverse the current through the loop each time the loop passes through the neutral plane.

An additional function of the commutator is, of course, to carry the current from the supply line, via the brushes, into the rotating armature.

Mechanical Motion from Electrical Energy

20–1 BASIC MOTOR ACTION

The term motor action was described briefly in Section 16–4. The sketch accompanying this explanation is reproduced for your convenience as Figure 20–1.

Figure 20–1 illustrates that a wire carrying electrons across a magnetic field will be pushed sideways. The current in the wire has a magnetic field of its own. The wire’s magnetic field combines with the externally applied magnetic field. The result of these combined fields causes the closely bunched, distorted lines of force to push the wire into the area that is less densely occupied by flux lines. This same idea is demonstrated, in a slightly different manner, by the sketch in Figure 20–2.

To apply this effect in an electric motor, examine the effect of an external magnetic field on a rectangular loop of wire. Assume that the wire is supplied with DC from a battery and that the external magnetic field is supplied by a permanent magnet, Figure 20–3. The sections of the loop that lie parallel to the field are not affected by the field. The side

of the loop marked A is pushed upward; the side marked B is pushed downward. Let us see why this happens.

Figure 20–4 represents a vertical cross-sectional view of the loop in the magnetic field shown in Figure 20–3. The heavy circles represent wires A and B in Figure 20–3. The X in the A circle represents electrons moving away from the observer (like the tail of an arrow flying away). The dot in the B circle represents electrons moving toward the observer (the point of an approaching arrow). The circular patterns around A and B represent the magnetic field of the current in these wires. (Using the left-hand rule, check the correctness of the direction arrows.)

Underneath A, the N S S magnetic field combines with the field of the wire, making a strong field under the wire. Above A, the field of the magnet and the field of the wire are in opposite directions. They cancel each other, making the weak field represented by the less-concentrated lines above A. Wire A is lifted by the strong magnetic field beneath. To account for this lifting effect, think of the N S S lines of force as both repelling each other and attempting to straighten themselves. A similar effect at B pushes wire B downward, much as a round stick is pushed down by a string, as shown in Figure 20–5.

The direction of motion of the wire can be found quickly by using a three-finger right-hand rule: With first finger, middle finger, and thumb at right angles to each other, forefinger 5 f ield, center finger 5 current, thumb 5 motion; see Figure 20–6.

Notice the similarity with Fleming’s left-hand rule for generators, as described in Section 18–3. The two rules may appear identical to the casual observer, but note the important difference:

The left-hand rule is used with generators, and the right-hand rule applies to motors.

This statement is, of course, based on the theory that defines current flow as a motion of electrons from negative to positive.

20–2 TORQUE AND ROTARY MOTION

Torque, also known as a moment of force, is a measure of the twisting effect that produces rotation about an axis. Torque is measured in pound-feet (or in similar units) and is calculated by multiplying the applied force by the radius of the turning circle.

Figure 20–7 shows examples of torque. Figure 20–7A represents a wagon wheel with a 4-foot diameter and the weight of a person (150 pounds) pressing downward on one of the spokes. Applying what we know about calculating torque,

2 ft x 150 lb = 300 lb-ft of torque

Note: Remember, radius is one-half the diameter.

Figure 20–7B shows two hands on a steering wheel with an 8-inch radius applying 5 pounds of pressure. Thus,

2⁄3 x 5 lb = 31⁄3 lb-ft of torque

The torque delivered by a motor is a more useful quantity than the single force pushing against the two vertical sides of the coil. The torque of an electric motor is

actually caused by the interaction of two magnetic fields, namely the main magnetic field (in our examples provided by the permanent magnet) and the magnetism created by the current flowing through the armature. Torque is a necessary quantity in the calculation of a motor’s horsepower, but we will discuss more about that later.

A Word of Caution:

Many students mistakenly confuse the term torque with work because of its similarity of calculation, the result being the mathematical product of force 3 distance.

Torque and work are not the same thing, and can exist independently of one another. To differentiate between the two terms, it is customary to call the unit of work the foot-pound and the unit of torque the pound-foot.

The lifting of one side of the loop and the pushing down of the other side creates a turning effect, or torque, on the loop of the wire. This combination of forces is the

torque that turns the armature of electric motors. This same method also explains the turning effect on the moving coil in a voltmeter or ammeter.

20–3 THE NEED FOR COMMUTATION

Imagine that the loop has rotated clockwise 90° from the position shown in Figure 20–3, until wires A and B are vertically aligned, as shown in Figure 20–8. Continued lifting of wire A and pushing down on wire B are useless. The loop is now perpendicular to the magnetic field and is said to be in the neutral plane.

When the loop is in the neutral plane, no torque is produced. To achieve continued rotation, the current direction in the loop must be reversed just as the loop enters the neutral plane. Since the loop is in motion, its inertia will carry it past the neutral plane position and, thus, continued rotation is assured.

This necessary reversal of the current is accomplished, for a single coil, by a two-segment commutator; see Figure 20–9. At the instant shown, electrons flow from the negative brush through A and return to the positive brush through B. As A is lifted to

the top of its rotation, the commutator segment that supplied electrons to A slides away from the negative brush and touches the positive brush; thus, the current in the loop is reversed. Momentum carries the loop past the vertical position. A is then pushed downward to the right, B is lifted to the left, and another half-turn of rotation continues. This description may help explain the need for commutators to reverse the current through the loop each time the loop passes through the neutral plane.

An additional function of the commutator is, of course, to carry the current from the supply line, via the brushes, into the rotating armature.

19–9 POWER LOSSES

All machines suffer power losses in the form of heat. Electrical machines, in particu- lar, suffer two kinds of power losses: copper losses (also known as I2R losses) and stray power losses; see Figure 19–36.

This phenomenon is sometimes explained by comparing the machine to a leaky water pipe, with one end of the pipe representing the input, and the other end the output. Such an illustration, depicting the losses on a motor, is represented in Figure 21–23. This analogy should make the fact clear that in all machines

Power input = Power output + All losses

As an exercise to further illustrate this point, make a sketch analogous to the generator shown in Figure 19–36.

Mechanical losses are caused by friction in bearings and brushes and by friction of the air, called windage. Windage loss varies with speed but is independent of load current. Core losses consist of hysteresis and eddy current losses. Hysteresis loss is due to molecule friction in the iron of the armature because of continual reversal of magnetization. Hysteresis loss increases with increase in flux density and increase in speed. Eddy current losses are due to small circulating, or eddying, currents.

Copper losses are a result of heat production by currents in the armature and field circuits of the machine. In other words:

Total I²R losses = I²R of armature + I²R of field(s)

EXAMPLE 19–2

Given: A shunt generator with an armature resistance of 1 ohm, delivering 9.5 amperes to a load at a terminal voltage of 120 volts; the shunt field has a resistance of 240 ohms, as shown in Figure 19–37.

Find:

a. Total I2R losses

b. The total emf generated

Efficiency of a Machine

Conversion of energy always incurs losses. In other words, the power output of a machine is always less than its power input; and the difference between the two represents the losses.

P_out = P_in – Losses

The ratio between the power output and the power input is described as the efficiency

of the machine. Efficiency is generally expressed as a percentage, as follows:

EXAMPLE 19–3

Given: The generator of Example 19–2, Figure 19–37, requiring a mechanical input of 2 horsepower.

Find:

a. The efficiency of the machine

b. The stray power losses

Solution

19–10 GENERATOR DATA AND RATINGS

The full-load rating of a generator is a statement of conditions that provide efficient operation without exceeding safe limits of speed and temperature. These data, which are supplied on the nameplate of the machine, include speed, voltage, power output (kW) or current output, and allowable temperature rise.

If operated at very low current output, efficiency is low. At a speed that is too low, air circulation is poor and overheating can result. Higher than normal current over a long time raises temperature and can damage insulation and burn the commutator and brushes. Standard voltages for larger DC generators are 125, 250, 275, and 600 volts.

The temperature rise allowed in a machine is a rise above 40°C, which is taken as a standard surrounding temperature. For example, the temperature of Class A insulation (enamel, oil-impregnated paper, and cotton) should not exceed 105°C. A machine with this insulation is rated 50°C temperature rise. This rating allows the average, or surface, temperature of a coil to be 90°C (40 1 50) while allowing for hot spots in the center of the coil to be 15°C higher than 90°C, which is the 105°C specified limit.

19–11 MAGNETOHYDRODYNAMIC (MHD) GENERATION

MHD generation, or energy conversion, uses the principles already discussed but in a different manner. Instead of moving a wire carrying electrons through a magnetic field, a stream of electrons and ions is made to move through a magnetic field. The high-speed electrons and positive ions are deflected in opposite directions by the magnetic field. Electrons

collect at one plate and positive ions at another. The excess negative and positive charges on the plates cause them to be at a different electrical potential, like the terminals of a battery. Think of the superheater in Figure 19–38 as a place for heating a gas, either by burning it or by applying heat from an external source. The temperature of the superheated gas is so high that gas molecules ionize, forming a cloud of electrons and positive ions.

The ionized gas blows through a nozzle, entering the magnetic field area at a tempera- ture of about 2,000°C and a velocity of over 1,500 miles per hour. As shown in Figure 19–38, the magnetic lines of force are directed at right angles to the page, as from an N pole above the page to an S pole behind the page. Just as electrons in a wire in an ordinary generator are forced to move in a direction relative to the magnetic field and to their direction of motion, electrons in this device are forced upward toward the anode.

The anode may be negatively charged already because of the previous accumulation of electrons. As more electrons come roaring by, the magnetic field deflects them. Their high kinetic energy slams them onto the anode, building up the negative charge still more. Positive ions are deflected in the opposite direction. They collide with the cathode and pick up electrons from it; thus the cathode maintains a positive charge (electron deficiency). Anode and cathode connect to the useful external circuit.

When and if MHD converters can be built to produce huge amounts of electrical energy, efficiency much higher than that for conventional steam turbine generator plants is possible. The size of the converter may be relatively small; Westinghouse has built an MHD generator that produces 2.5 kW from a unit about the size of this book.

Serious problems must yet be overcome. Extremely high temperatures are needed for the gases to ionize sufficiently to stay ionized rather than to recombine. Heat sources capable of producing the extremely high temperature must be developed. New materials must be found to resist critically high temperatures, or better use must be made of materials now available.

SUMMARY

• DC armatures carry coils in a series-parallel arrangement. There are two or more parallel paths though the armature, and each path consists of several coils in series.

• The magnetic field of the generator is usually supplied by current from the generator itself. This process is called self-excitation.

• Shunt field coils, in parallel with the load circuit, produce field magnetism that decreases slightly as the current output of the generator increases.

• Series field coils, in series with the load circuit, produce field magnetism that increases in proportion to the output current.

• Compound generators have both series and shunt fields.

• DC generators that are a part of specialized motor-control circuits are usually separately excited.

• Armature reaction, which is field distortion due to armature current, causes commutation difficulties that can be corrected by interpoles. It also causes field weakening, which can be corrected by compensating windings.

Achievement Review

1. A four-pole generator field has a flux density of 75,000 lines per square inch.

Each pole face is 5 inches square. Calculate the total flux.

2. Name three types of field coil arrangements for self-excited generators. Which gives the steadiest voltage output?

3. Name the three factors of greatest influence in determining the emf produced in a generator armature.

4. What is armature reaction? Name the two main disagreeable effects of armature reaction. How can both of these effects be corrected?

5. After standing idle for several weeks, an engine-driven DC compound generator is started up. It runs well but produces no voltage. Suggest reasonable causes and remedies.

6. If the efficiency of the generator is the only consideration, should the armature resistance be high or low? Should the shunt field resistance be high or low? Should the series field coil be high or low resistance?

7. Draw typical load–voltage characteristic curves for

a. A shunt generator

b. An undercompounded generator

c. An overcompounded generator

d. A series generator

8. Give three different reasons why the terminal voltage of a shunt generator decreases with an increase in load current.

9. A shunt generator is rated 125 volts, 25 kilowatts; armature resistance is 0.08 ohm; shunt field circuit resistance is 25 ohms. Determine

a. The induced emf in the armature at rated load

b. The watts loss in the armature

c. The watts loss in the shunt field circuit

d. The total power generated in the armature

10. A 10-kilowatt, 120-volt DC generator has an output of 120 volts at rated load.

With no load, a voltmeter across the output terminals reads 110 volts. Determine the voltage regulation. Is this machine a shunt, cumulative compound, or differential compound generator? How can you tell?

11. A 12-kilowatt, 240-volt, 1,500-revolutions-per-minute shunt generator has an armature resistance of 0.2 ohm and a shunt field resistance of 160 ohms. The stray power losses are 900 watts. Assuming shunt field current is constant, calculate

a. The efficiency at rated load

b. The efficiency at half-rated load

12. Explain how interpoles accomplish their purpose in a DC generator. State the polarity rule for interpoles.

13. A 10-kilowatt, 230-volt, long-shunt compound DC generator has efficiency 5 82%, armature resistance 5 0.15 ohm, series field 5 0.1 ohm, shunt field 5 100 ohms. At rated load, calculate

a. The armature current

b. The voltage across the brushes

c. The generated emf

d. The total copper losses

e. The horsepower of the prime mover

14. A separately excited 6-kilowatt generator has a terminal voltage of 135 volts at no load. At full load, the terminal voltage is 120 volts with speed and field excitation unchanged. Armature resistance 5 0.25 ohm. Find

a. The amount of voltage decrease caused by armature reaction

b. The voltage regulation

15. Complete the internal and external connections for the compound generator illustrated in the sketch below. This generator is to be connected as a cumulative compound long-shunt machine. The interpole field windings are to be a part of the armature circuit terminating at the connection points A1 and A2. Be sure the connections for all main field poles and interpoles are correct so that the proper polarities will be obtained.

19–9 POWER LOSSES

All machines suffer power losses in the form of heat. Electrical machines, in particu- lar, suffer two kinds of power losses: copper losses (also known as I2R losses) and stray power losses; see Figure 19–36.

This phenomenon is sometimes explained by comparing the machine to a leaky water pipe, with one end of the pipe representing the input, and the other end the output. Such an illustration, depicting the losses on a motor, is represented in Figure 21–23. This analogy should make the fact clear that in all machines

Power input = Power output + All losses

As an exercise to further illustrate this point, make a sketch analogous to the generator shown in Figure 19–36.

Mechanical losses are caused by friction in bearings and brushes and by friction of the air, called windage. Windage loss varies with speed but is independent of load current. Core losses consist of hysteresis and eddy current losses. Hysteresis loss is due to molecule friction in the iron of the armature because of continual reversal of magnetization. Hysteresis loss increases with increase in flux density and increase in speed. Eddy current losses are due to small circulating, or eddying, currents.

Copper losses are a result of heat production by currents in the armature and field circuits of the machine. In other words:

Total I²R losses = I²R of armature + I²R of field(s)

EXAMPLE 19–2

Given: A shunt generator with an armature resistance of 1 ohm, delivering 9.5 amperes to a load at a terminal voltage of 120 volts; the shunt field has a resistance of 240 ohms, as shown in Figure 19–37.

Find:

a. Total I2R losses

b. The total emf generated

Efficiency of a Machine

Conversion of energy always incurs losses. In other words, the power output of a machine is always less than its power input; and the difference between the two represents the losses.

P_out = P_in – Losses

The ratio between the power output and the power input is described as the efficiency

of the machine. Efficiency is generally expressed as a percentage, as follows:

EXAMPLE 19–3

Given: The generator of Example 19–2, Figure 19–37, requiring a mechanical input of 2 horsepower.

Find:

a. The efficiency of the machine

b. The stray power losses

Solution

19–10 GENERATOR DATA AND RATINGS

The full-load rating of a generator is a statement of conditions that provide efficient operation without exceeding safe limits of speed and temperature. These data, which are supplied on the nameplate of the machine, include speed, voltage, power output (kW) or current output, and allowable temperature rise.

If operated at very low current output, efficiency is low. At a speed that is too low, air circulation is poor and overheating can result. Higher than normal current over a long time raises temperature and can damage insulation and burn the commutator and brushes. Standard voltages for larger DC generators are 125, 250, 275, and 600 volts.

The temperature rise allowed in a machine is a rise above 40°C, which is taken as a standard surrounding temperature. For example, the temperature of Class A insulation (enamel, oil-impregnated paper, and cotton) should not exceed 105°C. A machine with this insulation is rated 50°C temperature rise. This rating allows the average, or surface, temperature of a coil to be 90°C (40 1 50) while allowing for hot spots in the center of the coil to be 15°C higher than 90°C, which is the 105°C specified limit.

19–11 MAGNETOHYDRODYNAMIC (MHD) GENERATION

MHD generation, or energy conversion, uses the principles already discussed but in a different manner. Instead of moving a wire carrying electrons through a magnetic field, a stream of electrons and ions is made to move through a magnetic field. The high-speed electrons and positive ions are deflected in opposite directions by the magnetic field. Electrons

collect at one plate and positive ions at another. The excess negative and positive charges on the plates cause them to be at a different electrical potential, like the terminals of a battery. Think of the superheater in Figure 19–38 as a place for heating a gas, either by burning it or by applying heat from an external source. The temperature of the superheated gas is so high that gas molecules ionize, forming a cloud of electrons and positive ions.

The ionized gas blows through a nozzle, entering the magnetic field area at a tempera- ture of about 2,000°C and a velocity of over 1,500 miles per hour. As shown in Figure 19–38, the magnetic lines of force are directed at right angles to the page, as from an N pole above the page to an S pole behind the page. Just as electrons in a wire in an ordinary generator are forced to move in a direction relative to the magnetic field and to their direction of motion, electrons in this device are forced upward toward the anode.

The anode may be negatively charged already because of the previous accumulation of electrons. As more electrons come roaring by, the magnetic field deflects them. Their high kinetic energy slams them onto the anode, building up the negative charge still more. Positive ions are deflected in the opposite direction. They collide with the cathode and pick up electrons from it; thus the cathode maintains a positive charge (electron deficiency). Anode and cathode connect to the useful external circuit.

When and if MHD converters can be built to produce huge amounts of electrical energy, efficiency much higher than that for conventional steam turbine generator plants is possible. The size of the converter may be relatively small; Westinghouse has built an MHD generator that produces 2.5 kW from a unit about the size of this book.

Serious problems must yet be overcome. Extremely high temperatures are needed for the gases to ionize sufficiently to stay ionized rather than to recombine. Heat sources capable of producing the extremely high temperature must be developed. New materials must be found to resist critically high temperatures, or better use must be made of materials now available.

SUMMARY

• DC armatures carry coils in a series-parallel arrangement. There are two or more parallel paths though the armature, and each path consists of several coils in series.

• The magnetic field of the generator is usually supplied by current from the generator itself. This process is called self-excitation.

• Shunt field coils, in parallel with the load circuit, produce field magnetism that decreases slightly as the current output of the generator increases.

• Series field coils, in series with the load circuit, produce field magnetism that increases in proportion to the output current.

• Compound generators have both series and shunt fields.

• DC generators that are a part of specialized motor-control circuits are usually separately excited.

• Armature reaction, which is field distortion due to armature current, causes commutation difficulties that can be corrected by interpoles. It also causes field weakening, which can be corrected by compensating windings.

Achievement Review

1. A four-pole generator field has a flux density of 75,000 lines per square inch.

Each pole face is 5 inches square. Calculate the total flux.

2. Name three types of field coil arrangements for self-excited generators. Which gives the steadiest voltage output?

3. Name the three factors of greatest influence in determining the emf produced in a generator armature.

4. What is armature reaction? Name the two main disagreeable effects of armature reaction. How can both of these effects be corrected?

5. After standing idle for several weeks, an engine-driven DC compound generator is started up. It runs well but produces no voltage. Suggest reasonable causes and remedies.

6. If the efficiency of the generator is the only consideration, should the armature resistance be high or low? Should the shunt field resistance be high or low? Should the series field coil be high or low resistance?

7. Draw typical load–voltage characteristic curves for

a. A shunt generator

b. An undercompounded generator

c. An overcompounded generator

d. A series generator

8. Give three different reasons why the terminal voltage of a shunt generator decreases with an increase in load current.

9. A shunt generator is rated 125 volts, 25 kilowatts; armature resistance is 0.08 ohm; shunt field circuit resistance is 25 ohms. Determine

a. The induced emf in the armature at rated load

b. The watts loss in the armature

c. The watts loss in the shunt field circuit

d. The total power generated in the armature

10. A 10-kilowatt, 120-volt DC generator has an output of 120 volts at rated load.

With no load, a voltmeter across the output terminals reads 110 volts. Determine the voltage regulation. Is this machine a shunt, cumulative compound, or differential compound generator? How can you tell?

11. A 12-kilowatt, 240-volt, 1,500-revolutions-per-minute shunt generator has an armature resistance of 0.2 ohm and a shunt field resistance of 160 ohms. The stray power losses are 900 watts. Assuming shunt field current is constant, calculate

a. The efficiency at rated load

b. The efficiency at half-rated load

12. Explain how interpoles accomplish their purpose in a DC generator. State the polarity rule for interpoles.

13. A 10-kilowatt, 230-volt, long-shunt compound DC generator has efficiency 5 82%, armature resistance 5 0.15 ohm, series field 5 0.1 ohm, shunt field 5 100 ohms. At rated load, calculate

a. The armature current

b. The voltage across the brushes

c. The generated emf

d. The total copper losses

e. The horsepower of the prime mover

14. A separately excited 6-kilowatt generator has a terminal voltage of 135 volts at no load. At full load, the terminal voltage is 120 volts with speed and field excitation unchanged. Armature resistance 5 0.25 ohm. Find

a. The amount of voltage decrease caused by armature reaction

b. The voltage regulation

15. Complete the internal and external connections for the compound generator illustrated in the sketch below. This generator is to be connected as a cumulative compound long-shunt machine. The interpole field windings are to be a part of the armature circuit terminating at the connection points A1 and A2. Be sure the connections for all main field poles and interpoles are correct so that the proper polarities will be obtained.

19–6 THREE TYPES OF SELF-EXCITED GENERATORS (SERIES, SHUNT, AND COMPOUND)

The Series Generator

Look back at Figure 19–19 and recall that the field of the series generator carries the entire load current to the external circuit; therefore, the greater the load current, the greater the magnetic field strength; see Figure 19–27. If the generator is started with the external circuit disconnected from the generator terminals, there is no buildup of field. The small voltage due to residual magnetism cannot produce any current at all in an open circuit. If a small load current is taken from the generator, its output voltage is low. If a reasonably high load current is taken, the output voltage is high. If an ordinary parallel- wired lighting circuit is used as the load and two or three lamps turned on, the lamps are dim. The more lamps that are turned on, the brighter each lamp becomes. However, a little

of this voltage-increasing effect can be a good thing; it illustrates the effect of the series field of a cumulative compound generator; see Figure 19–27. The series generator, impractical for most jobs, does have one interesting application: It can be used in a simple motor-control system, driving a series motor at nearly constant speed with changing load on the motor (Chapter 21).

The Shunt Generator

We have seen, in Figure 19–20, that a shunt generator has its field winding connected parallel to the armature. Comparing this arrangement with that of the series generator, we find that the shunt field coil is constructed of many turns of relatively thin wire. Recall that magnetic field strength is proportional to the number of ampere-turns; thus, the shunt field coil requires relatively little current, generally amounting to less than 3% of the total current supplied by the armature.

With the field coil parallel to the armature, it is reasonable to expect a stable output voltage as long as the generator is driven at constant speed. This is true, indeed, except that the voltage is gradually reduced as the load on the generator is increased; see Figure 19–28.

In our discussion, we distinguish between the generated emf (when the generator is unloaded) and the terminal voltage (delivered to the load). The difference between these two values represents the drop in output voltage that accompanies the increase in load current. This reduction in voltage is due to two factors, as follows:

1. Armature reaction weakens the field, thereby decreasing the generated emf; see Figure 19–29 (drop A).

2. The IR drop of the armature. There is only a little resistance in the armature winding but enough to cause a voltage drop (IR drop). This IR drop, which varies proportionally with the load current, is lost to the load and causes a further reduction in output voltage; see Figure 19–29 (drop B).

Both of these effects reduce the output voltage. Reduced output voltage causes reduced field current and therefore field flux. With reduced field flux, there is a further reduction in generated emf; see Figure 19–29 (drop C).

Assume that we have a shunt generator with armature resistance equal to 0.4 ohm, rated 10-ampere output current. When operating with no load (external circuit open), we find that the emf is 121 volts. When operated at its rated 10-ampere load, there is a 4-volt drop, or waste, in the armature. (E 5 IR 5 10 3 0.4 5 4 V. Four volts are used in pushing electrons through the generator itself.) This 10-ampere load in the armature also distorts and weakens the field so that there is a decrease in the generated emf of 3 volts. Because of all these voltage deficiencies, the field current and flux are reduced; thus, the generated emf is less by another 4 volts. Because of armature reaction and reduced field current, 121 2 7 5 114 volts are generated. After subtracting the 4 volts used in the armature, there is an output voltage at the terminal of 110 volts.

The characteristic of shunt generators dropping their voltage with increased load is not all bad. In extreme cases of overload, such as a short circuit, the generator will pro- tect itself from damage by reducing the field excitation and, correspondingly, the output voltage. For example, if the generator is overloaded to 15 amperes instead of 10 amperes, increased armature reaction and the resulting reduction in field current bring the generated emf down to 109 volts. Fifteen amperes through the 0.4-ohm armature use 6 volts, so the terminal voltage is down to 103 volts.

Voltage Regulation

As a measurable quantity, the term voltage regulation means the percentage change of voltage from rated-load to no-load conditions.

The Compound Generator

The compound generator is designed to compensate for the voltage losses that characterize shunt generators under the influence of increased load. Recall that in a series generator, just the opposite phenomenon occurs: The voltage increases with increasing load. By adding a series winding to the shunt generator, we can combine the features of both windings to provide a more stable output voltage.

Let us examine the effect of adding series field coils to the shunt generator described previously. At a 10-ampere load with a series field coil present, we still have the field- weakening effect of armature reaction and the 4-volt IR drop on the armature, plus a possible 1-volt additional IR drop in the series field. All of these effects can be overcome by adding enough turns of the wire to the field. These turns are connected in series with the load; thus, the 10 amperes in these turns can add to the magnetizing effect of the shunt field coil, increasing the generated emf. The generated emf can readily be brought up to 126, which, less the 5-volt internal IR drops, makes the output voltage 121, the same as at no load. A generator with open-circuit voltage equal to rated load voltage is called flat compounded; see Figure 19–30.

A generator can be overcompounded. Enough series ampere-turns can be provided to make the output voltage rise above no-load voltage as the output current increases. (Compare with series generators.) Usually, compound generators are built with enough series turns to accomplish overcompounding. The user can adjust the current in the series winding to suit specific operating conditions. Adjustment of the diverter rheostat allows some load current to bypass the series coils, as illustrated in Figure 19–31, and thereby to change the degree of compounding. For instance, if the effect of the series coil is severely limited, the shunt coil will dominate the output characteristics of the generator. Such a machine is said to be undercompounded.

The same circuit of Figure 19–31 is shown schematically in Figure 19–32 to illustrate two points.

1. The generator is connected as a short-shunt generator. Remember, compound generators can be connected either in a short-shunt or long-shunt configuration.

2. The drawing shows a rheostat in the shunt field circuit for the purpose of varying the output voltage. As explained earlier in this chapter, with this rheostat, the operator can weaken or strengthen the magnetic field, thereby changing the output voltage of the generator.

Before leaving the subject of compound generators, let us have another look at Figure 19–30, and note the term differentially compounded. Most generators are cumulatively compounded; that is, the two windings on the pole pieces (series and shunt) are wound in the same direction, so that their magnetic fields will reinforce each other; see Figure 19–31. In a differentially compounded generator, by contrast, the two magnetic fields are opposing each other. Not many generators are differentially compounded.

19–7 SEPARATELY EXCITED GENERATORS

Two general ways of providing a magnetic field for a generator have been mentioned:

1. Permanent magnet (very limited application)

2. Self-excitation—shunt, series, or compound (the most widely used method)

A third possibility is a separate current source energizing the field coils of the generator, as illustrated in Figure 19–33. Normally, this method is used only as a part of a specialized motor-control circuit, such as Ward Leonard system, Rototrol system, or Amplidyne control system, to name a few. The purpose of these systems is to permit the operator to select any specific speed, after which the system holds the motor at that speed regardless of variations in the load on the motor. Separate excitation systems of this type are used in mine hoists, steel-mill rolling mills, paper machines, diesel-electric locomotives, and other similar devices.

19–8 GENERATOR CALCULATIONS

The following paragraphs are not intended to provide enough details to illustrate all of the factors that must be calculated by a generator designer. They are intended only to point out the basic principles of the energy conversion that goes on in a generator.

Generator emf

As stated before, generator emf is proportional to field strength, number of wires on the armature, and rpm of the armature. When the field strength, armature windings, and rpm of the armature are known, the number of lines of force cut per second can be found. The cutting of 100,000,000 lines by wire each second makes 1 volt.

EXAMPLE 19–1

Given: An armature as shown in Figure 19–34. (This is similar to the armature in Figures 19–13 and 19–14.) The armature has eight coils, each coil consisting of

40 turns, operating at 1,200 rpm, between two field poles, each pole having 15 square inches of face area and a flux density of 80,000 lines per square inch.

Find: The emf generated.

Solution

Figure 19–34 shows that the coils are in two parallel groups, with four coils in series in each group. The emf is produced by four coils in series, not eight. Therefore, we need to take into account four coils of 40 turns each 5 160 turns. Since the purpose of this calculation is to find the average emf, we need not be concerned about differences in instantaneous voltages in the coils.

Each turn of wire in the coil has two sides, both of which cut the entire field twice (once up and once down) during each revolution. The 160 turns, then, have to be multiplied by 4 to give the number of times that the entire field is cut by wire each revolution. The field is cut 640 times.

The total field flux is 80,000 lines per sq in. 3 15 sq in. 5 1,200,000 lines. During one rotation, 1,200,000 lines are cut 640 times: 640 3 1,200,000 5 768,000,000 total lines of force cut.

The coils rotate at 1,200 rpm, which is 20 revolutions per second. The total cutting of lines per second is 768,000,000 times 20. The emf generated is

Planning a generator design to produce a given emf involves a sensible choice of turns, flux, rpm, and type of winding—based on both theory and experience—and takes into account any special demands on the generator in use.

Emf vs.Terminal Voltage

The emf that we just calculated in the preceding problem is not the same as the voltage delivered to the terminals of the load. To understand why, consider the following: The armature has some resistance, say 0.4 ohm; and the brushes, riding on the commutator, have resistance of about 0.05 ohm. These resistances are shown as RA, lumped together outside the armature, in the schematic diagram of Figure 19–35.

Assuming that 10 amperes is flowing through the armature, there will be a voltage drop of 4.5 volts in the armature, which is lost to the load. Think of it as a series circuit, and you will see that only 149.1 volts will be available at the terminals of the load.

Kirchhoff’s voltage law is proven once again and is stated now like this:

Output voltage = Generated emf – IR drop in armature and brushes