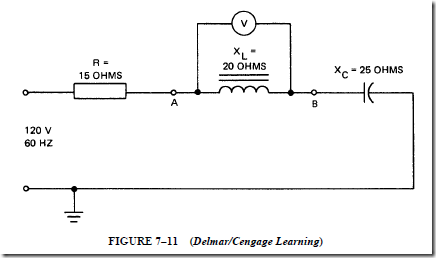
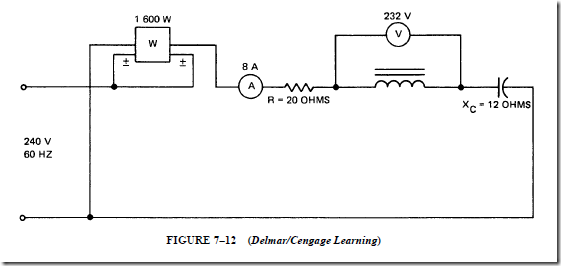
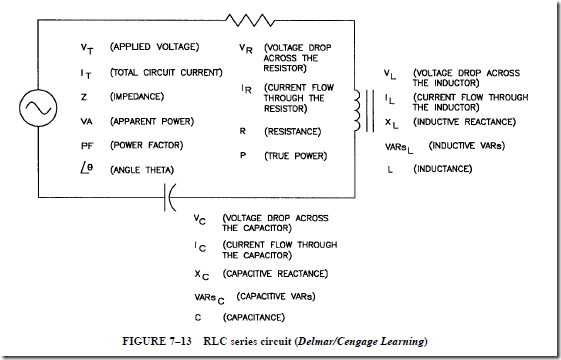
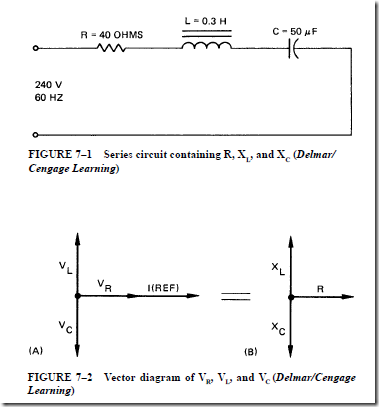
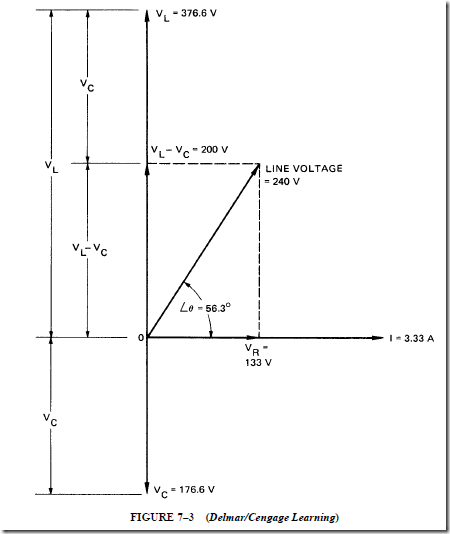
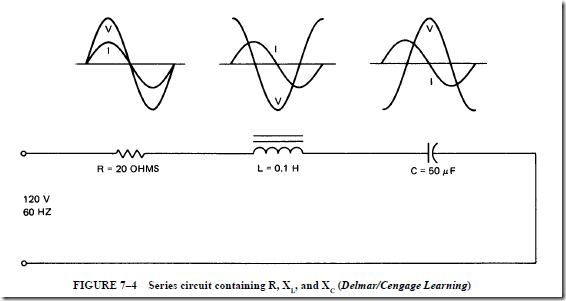
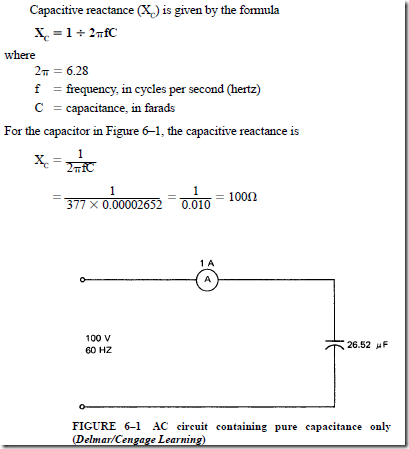
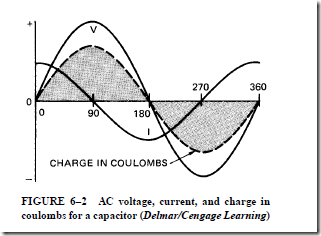
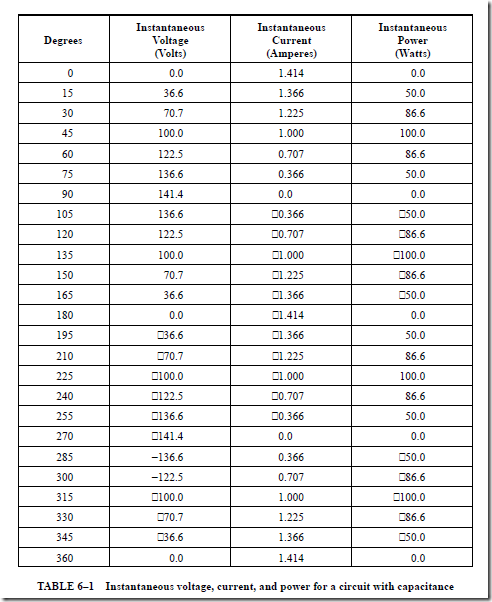
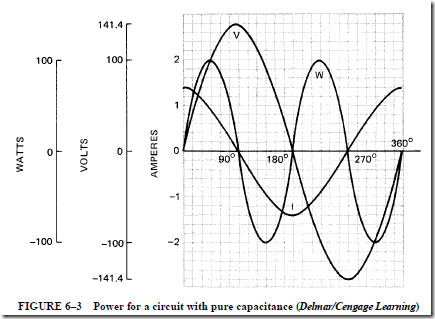
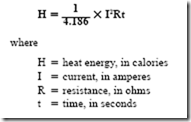
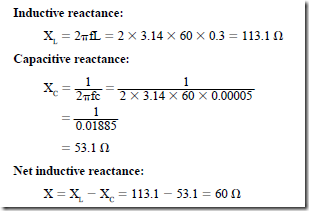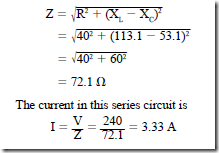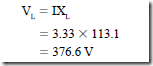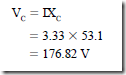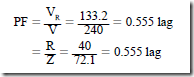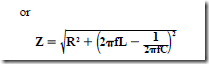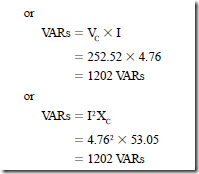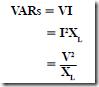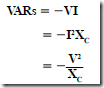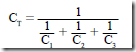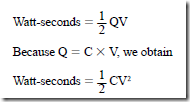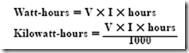RL TIME CONSTANTS
A discussion of time constants for RL series circuits is given here because the exponential curves and calculations involved are similar to those for RC series circuits.
Current in an RL Circuit
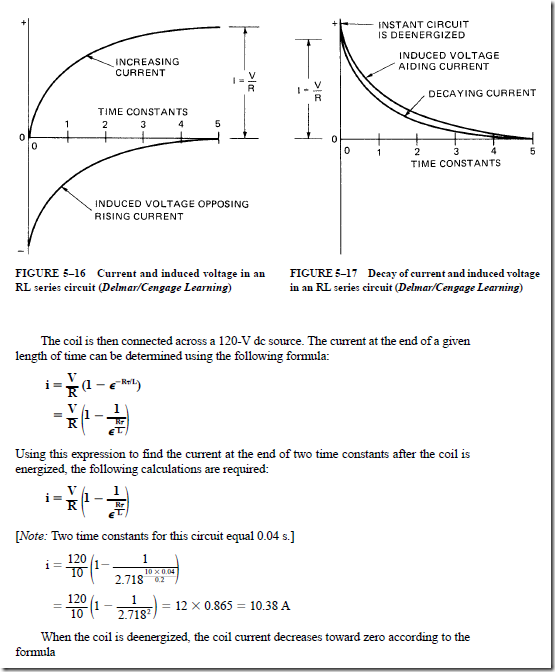
Any inductance coil is really a combination of inductance and resistance in series. If the coil is connected to a dc supply, the final value of current is given by Ohm’s law, I = V/R. However, the current does not rise to the Ohm’s law value instantaneously. The current increases exponentially because the inductance opposes the change in current (Figure 5–16).
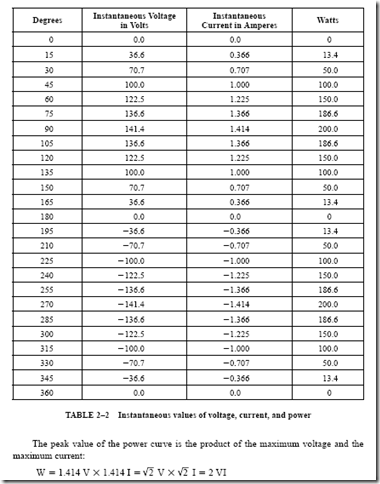
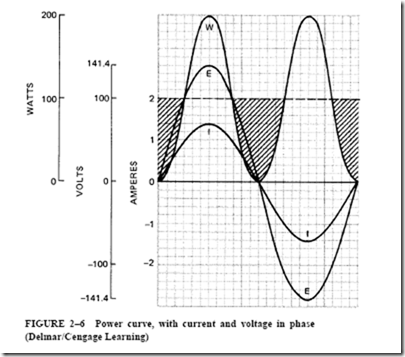
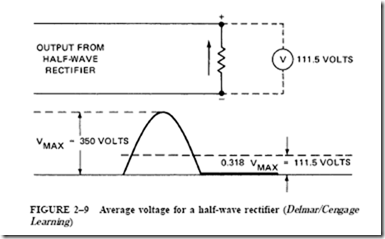
RL Exponential Current Curve. The exponential curve for current in an RL circuit is shown in Figure 5–16. When the circuit is energized, the induced voltage is at its maximum value. It then decreases as the rate of increase of current becomes less. The current reaches its Ohm’s law value at the end of five time constants. At this point, the induced voltage is zero.
When the circuit is deenergized, the decay of current causes an induced voltage. This voltage attempts to maintain the current. Figure 5–17 shows the gradual decay of current as the induced voltage decreases. At the end of five time constants, the current and the induced voltage are close to zero.
The RL Time Constant
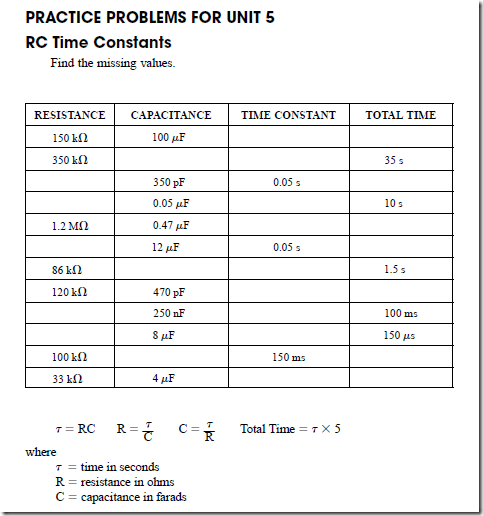
It was shown for RC circuits that one time constant is equal to the resistance in ohms times the capacitance in farads: T = RC.
In an RL circuit, the current at the end of one time constant is 63.2% of its final value as determined by Ohm’s law. The time constant for an RL circuit is equal to the ratio of the inductance in henrys to the resistance in ohms: T = L –: R.
For example, assume that a coil has an inductance of 0.2 H and a resistance of 10 D.
One time constant is found to be
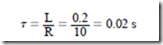
APPLICATIONS OF CAPACITORS
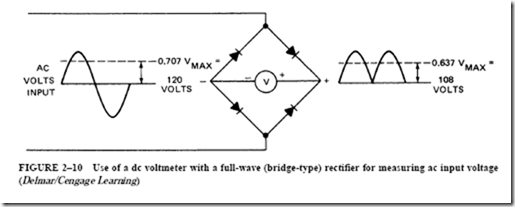
There are many practical applications for capacitors in electricity and electronics. For example, in power applications, capacitors are used to improve the power factor of distribution circuits. The starting torque of certain types of single-phase induction motors can be improved by the addition of capacitors. Capacitors are used with rectifier units to change pulsating direct current to a constant dc. Nonpulsating direct current is used with electronic components.
Capacitors have many applications in communication electronics at audio, radio, and video frequencies. Capacitors are used in special phase shift circuits to control the plate current conduction of thyratron and ignitron tubes. Capacitors are also used in electronic time-delay systems and in phototube circuits, as well as in numerous other industrial applications. Examples of typical capacitors are shown in Figure 5–18.
TYPES OF CAPACITORS
The most basic form of fixed capacitor consists of two metal plates separated by a thin dielectric material. This material may be ceramic or mica. This simple capacitor is enclosed in a plastic case. Two leads pass through the case and connect to the plates. In some capacitors, a number of plates are placed between sheets of dielectric with alternate plates connected in parallel. This arrangement increases the plate area, resulting in an increase in the capacitance. Figure 5–19 shows one type of simple capacitor. Such a capacitor is usually rated in microfarads or picofarads.
Tubular Capacitors
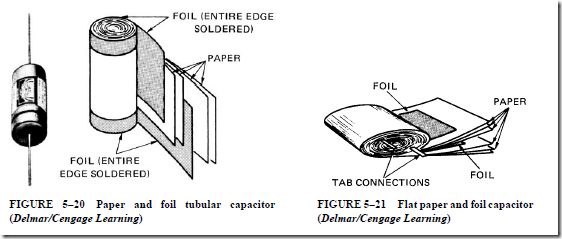
A second type of capacitor is shown in Figure 5–20. The capacitance rating of this tubular paper capacitor is larger than that of a mica capacitor. The capacitor consists of a strip of waxed paper placed between two strips of tinfoil or aluminum foil. The paper and foil strips are about an inch wide and 8 to 12 ft in length. The strips are rolled and placed in
a small plastic or metal cylinder. The resulting capacitor is physically small, but has a large plate area and a large value of capacitance.
The tinfoil or aluminum foil plates are often separated by a thin film of paper treated with an oil, or by a film of plastic. The paper capacitor (Figure 5–21) is enclosed in a flat case or an oil-filled can.
Ceramic Capacitors
Ceramic capacitors consist of a ceramic dielectric and silver plates. The dielectric is a ceramic compound such as barium titanate or titanium dioxide. The dielectric is usually in the form of a disc. The silver plates are secured to each side of this thin ceramic disc.
Ceramic capacitors have capacitance ratings as high as 2.0 p,F. This rating is large considering the relatively small size of the capacitor.
Electrolytic Capacitors
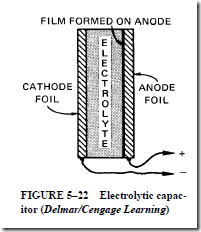
Another type of capacitor is used for direct-current applications generally. An electrolytic capacitor is shown in Figure 5–22. The positive plate is made from aluminum foil. This plate is immersed in an electrolyte consisting of a borax solution. The electrolyte serves as the negative plate of the capacitor. A second piece of aluminum foil is placed between the electrolyte and the negative terminal of the capacitor. When the capacitor is energized from a dc source, an insulating film of oxide develops on the positive aluminum foil. This film forms a very thin dielectric. The extremely thin dielectric means that the electrolytic capacitor has a very high capacitance rating for its physical size.
A more popular type of capacitor is the dry electrolytic capacitor. The electrolyte in this type of capacitor is gauze saturated with a borax solution. This dry capacitor has the advantage that there is no liquid electrolyte to leak from the case.
Connecting Electrolytic Capacitors. When connecting an electrolytic capacitor into a dc circuit, the positive aluminum plate must be connected to the positive side of the circuit. If this type of capacitor is installed with its connections reversed, the dielectric will be punctured. With the wet electrolytic capacitor, the dielectric will repair itself if the capacitor is reconnected properly. The dry capacitor, however, is permanently damaged if the connections are reversed.
AC Electrolytic Capacitor. The electrolytic capacitor described in the previous para- graphs cannot be used in an alternating-current circuit. Because the voltage is continually changing direction, the dielectric of the capacitor will be punctured repeatedly. However, a form of the electrolytic capacitor known as a nonpolarized electrolytic capacitor can be used in alternating-current circuits. This capacitor is really two wet, self-healing electro- lytic capacitors assembled in a series back-to-back arrangement. The like plates of these
capacitors are connected together. When an ac voltage is applied to the two outside terminals, one capacitor will be connected properly. At the same time, the dielectric of the second capacitor will be punctured. Then, in the other half-cycle, this process is reversed. Thus, there is always one capacitor connected properly, regardless of the direction of the ac voltage.
Air Capacitors
A common form of the variable-air capacitor is shown in Figure 5–23. One group of plates is mounted so they are movable with respect to a group of fixed plates. The movable plates are called the rotor and the fixed plates are called the stator. This type of capacitor is ideal for tuning radio receivers because the capacitance can be varied at low values, in the order of picofarads. The typical capacitance range of a variable air capacitor is between 500 pF and zero.
The trimmer capacitor (Figure 5–24) has two metal plates with an air dielectric. The spacing between the plates can be changed by means of an insulated setscrew. As the set- screw is tightened, the spacing is decreased. As a result, the capacitance is increased.
Capacitor Symbols
The symbol for any type of fixed capacitor is shown in Figure 5–25A. In schematic diagrams, the curved portion of the symbol is connected to ground, or to the low or negative voltage side of the circuit. The symbols for variable capacitors are given in Figure 5–25B.
CAPACITOR MARKINGS
Different types of capacitors are marked in different ways. Capacitance and voltage values are usually written directly on large ac oil-filled paper capacitors. The same is true for most electrolytic and small nonpolarized capacitors. Other types of capacitors, how- ever, depend on color codes or code numbers and letters to indicate the capacitance value,
tolerance, and voltage rating. Although color coding for capacitors has been abandoned in favor of direct marking by most manufacturers, it is still used by some. Also, many older capacitors with color codes are still in use. For this reason, this text will discuss color coding for several different types of capacitors.
Unfortunately, there is no actual set standard used by all manufacturers. The color codes presented are probably the most common. An identification chart for “postage stamp” mica capacitors and tubular paper or tubular mica capacitors is shown in Figure 5–26. It should be noted that most “postage stamp” mica capacitors use a five-dot color code. There are six-dot color codes, however. When a six-dot color code is used, the third color dot rep- resents a third digit and the rest of the code is the same. The capacitance values given are in picofarads. Although these markings are typical, there is no actual standard, and it may be necessary to use manufacture’s literature to determine the true values. A second method for
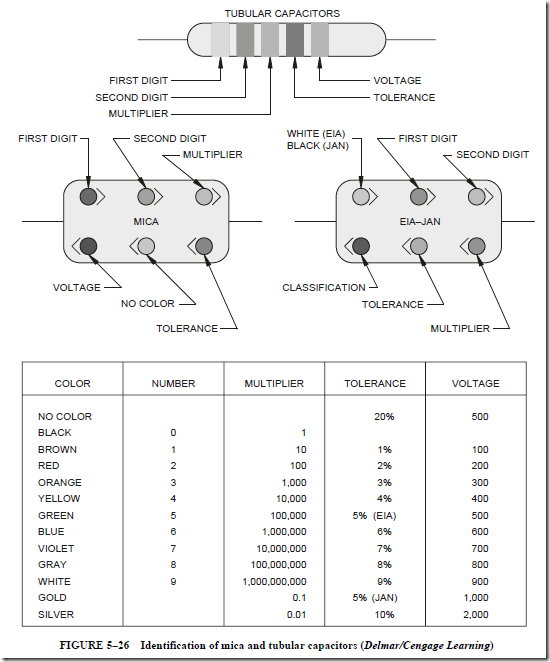
color coding mica capacitors is called the Electronic Industries Association (EIA) standard, or the Joint Army-Navy (JAN) standard. The JAN standard is used for electronic components intended for military use. When the EIA standard is employed, the first dot will be colored white. In some instances, the first dot may be colored silver instead of white. This indicates that the capacitor’s dielectric is paper instead of mica. When the JAN standard is used, the first dot will be colored black. The second and third dots represent digits, the fourth dot is the multiplier, the fifth dot is the tolerance, and the sixth dot indicates classes A through E of temperature and leakage coefficients.
Temperature Coefficients
The temperature coefficient indicates the amount of capacitance change with tem- perature. Temperature coefficients are listed in parts per million (ppm) per degree Celsius (°C). A positive temperature coefficient indicates that the capacitor will increase its capacitance with an increase in temperature. A negative temperature coefficient indicates that the capacitance will decrease with an increase in temperature.
Ceramic Capacitors
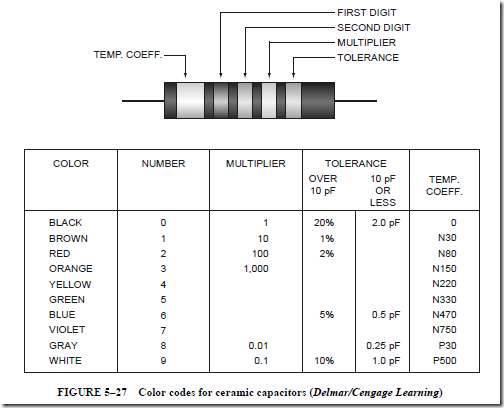
Another capacitor that often uses color codes is the ceramic capacitor (Figure 5–27). This capacitor will generally have one band that is wider than the others. The wide band indicates the temperature coefficient, and the other bands are first and second digits, multiplier, and tolerance.
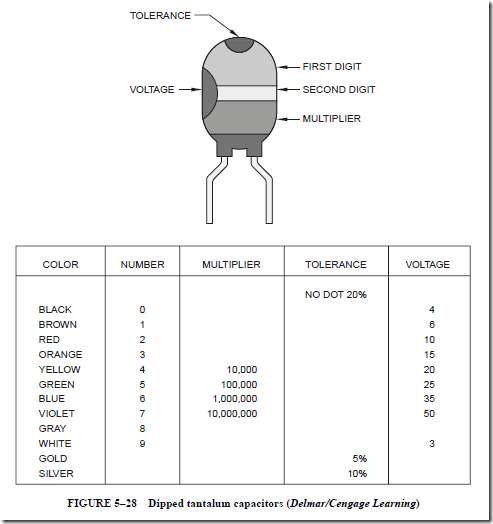
Dipped Tantalum Capacitors
A dipped tantalum capacitor is shown in Figure 5–28. This capacitor has the general shape of a match head but is somewhat larger in size. Color bands and dots determine the value, tolerance, and voltage. The capacitance value is given in picofarads.
Film Capacitors
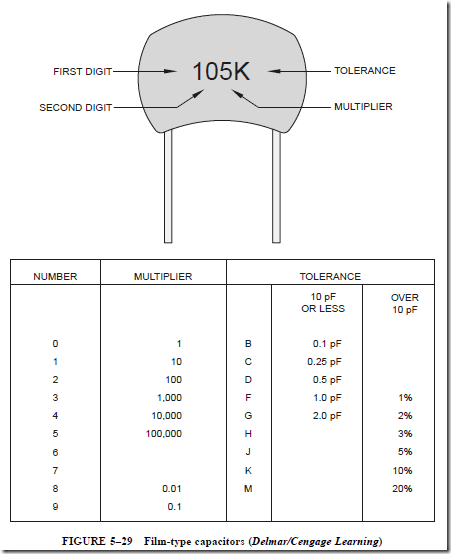
Not all capacitors use color codes to indicate values. Some capacitors use numbers and letters. A film-type capacitor is shown in Figure 5–29. This capacitor is marked “105K.” The value can be read as follows:
1. The first two numbers indicate the first two digits of the value.
2. The third number is the multiplier. Add the number of zeros to the first two numbers indicated by the multiplier. In this example, add five zeros to 10. The value is given in picofarads. This capacitor has a value of 1,000,000 pF, or 1 p,F.
3. The K symbol indicates the tolerance. In this example, K indicates a tolerance of ±10%.
SUMMARY
• The elementary capacitor consists of two metal plates separated from each other by a dielectric (insulating material).
1. During the charge process, electrons flow from the negative side of the source to one plate and from the second plate back to the source.
2. There is almost no flow of electrons through the dielectric material.
3. The movement of electrons continues until the potential difference across the two metal plates is equal to the source voltage. At this point, the capacitor is said to be fully charged.
4. The charges on the plates of the capacitor act on the electrons of the atoms in the dielectric and cause the orbits of these electrons to be distorted.
5. An electrostatic field created by the charged plates maintains the distortion of the electron orbits in the dielectric atoms. This electrostatic field stores electrical energy.
6. The distortion dissipates once the capacitor is discharged. The electron orbits of the atoms of the dielectric return to their normal pattern.
• Capacitance is the property of a circuit, or circuit component, that allows it to store electrical energy in electrostatic form.
1. Capacitance is measured in farads. A capacitor has a capacitance of one farad when a change of one volt across its plates results in a charge movement of one coulomb:
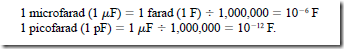
2. The capacitance of a capacitor can be increased by
a. increasing the plate area to increase the area of dielectric under stress.
b. moving the metal plates closer together to decrease the thickness of the dielectric, resulting in a greater stress.
c. using a dielectric with a higher dielectric constant.
(1) The dielectric constant of an insulating material measures the effective- ness of the material when used as the dielectric of a capacitor. This gives a value indicating the degree of distortion of the electron orbits in the dielectric for a given applied voltage.
(2) The dielectric constants of all other materials are measured against air, which is assumed to be one.
• Circuit components other than capacitors may create a capacitance effect.
1. When two wires of a circuit are separated by air, they will act as a capacitor.
2. Adjacent turns of a coil winding, which are separated only by the insulation of the wire, will have some capacitance effect.
• The charge on the plates of a capacitor for a given applied voltage is directly proportional to the capacitance of the capacitor:
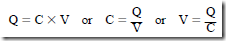
• Dielectric materials are given a dielectric strength rating:
1. This rating is stated as either “volts per centimeter” or “volts per mil” of dielectric thickness required to break down the dielectric.
2. It is not the same as the dielectric constant.
• The formulas used to determine the capacitance of a two-plate capacitor are
Measurements in inches:
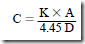
Measurements in centimeters:
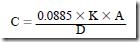
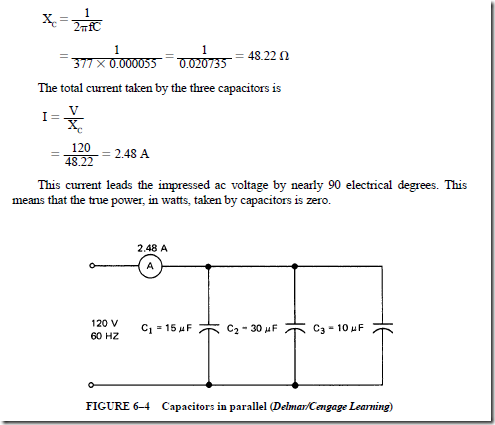
• The total capacitance when capacitors are connected in parallel is given by
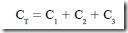When capacitors are connected in parallel, the effect is the same as increasing the number of plates or the area of the plates.
• The total capacitance when capacitors are connected in series is given by
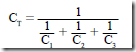
When capacitors are connected in series, the effect is equivalent to increasing the thick- ness of the dielectric of one capacitor, resulting in less capacitance.
• The formulas for total capacitance can be used only when all of the values are in the same unit of capacitance measurement, either microfarads or picofarads.
• The amount of energy stored in a capacitor is measured in joules or watt-seconds:
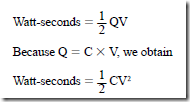
• The amount of charge on the plates of a capacitor is a function of the current and time.
1. As the value of the current increases, less time is required to charge the capacitor fully.
2. The time required for a given voltage to build up across the capacitor can be con- trolled by increasing or decreasing the charging current
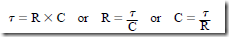
where T is the Greek letter tau, the letter symbol for a time constant expressed in seconds.
• One time constant is the time, in seconds, required for a completely discharged capacitor to charge to 63% of the source voltage.
1. For all practical purposes, it is assumed that the capacitor is fully charged at the end of five time constants.
2. For all practical purposes, it is assumed that a fully charged capacitor will be completely discharged at the end of five time constants of discharge.
• The relationship of the current to the supply voltage for a capacitor being charged can be found at any instant:
• When connecting an electrolytic capacitor, the plates must be properly connected.
1. For the wet electrolytic capacitor, the dielectric will repair itself after being punctured as a result of reversed connections.
2. If the connections of the dry electrolytic capacitor are reversed, the dielectric is permanently damaged.
3. The electrolytic capacitor cannot be used in an alternating-current circuit. How- ever, a nonpolarized electrolytic capacitor can be used in ac circuits.
Achievement Review
1. List three factors that affect the capacitance of a capacitor.
2. Define the basic unit of measurement of capacitance.
3. A capacitor takes a charge of 0.05 coulomb (C) when connected across a 250-V source. Determine the capacitance of the capacitor in microfarads.
4. Explain what is meant by the term dielectric constant.
5. A paper capacitor consists of two aluminum foil plates, each 10 ft long and 1.5 in. wide. The waxed paper separating the two plates has a thickness of 0.04 in. The dielectric constant is assumed to be 2. Determine the capacitance of the capacitor, using both formulas:
6. Three capacitors have ratings of 20 p,F, 60 p,F, and 30 p,F, respectively. These capacitors are connected in parallel across a 220-V dc source. Determine
a. the total capacitance of the three capacitors connected in parallel.
b. the total charge, in coulombs, taken by the three capacitors in parallel when connected across a 220-V dc source.
7. The three capacitors in question 6 are connected in series across a 220-V dc source. Determine
a. the total capacitance of the three capacitors connected in series.
b. the total charge, in coulombs, taken by the three capacitors in series when connected across a 220-V dc source.
8. Explain what is meant by the term dielectric strength rating.
9. List five practical applications for capacitors.
10. Determine the energy, in watt-seconds, stored in a 100-p,F capacitor when connected across a 400-V dc source.
11. A 100-p,F capacitor is connected in series with a 500-V dc voltmeter across a 400-V dc supply. The voltmeter has a resistance of 1000 D/V.
a. Determine the time, in seconds, represented by one time constant for this RC series circuit.
b. Determine the voltage across the capacitor plates at the end of one time constant when the capacitor is on charge.
12. Using the circuit given in question 11, determine
a. the voltage across the capacitor plates at the end of two time constants, when the capacitor is charging.
b. the voltage across the capacitor plates, at the end of five time constants, when the capacitor is charging.
13. Using the circuit given in question 11, determine the voltage across the plates of the capacitor, at the end of one time constant, when the capacitor is discharging.
14. At the end of one time constant, what is the charging current in amperes for the RC series circuit given in question 11?
15. Determine the time constant, in seconds, for an inductor coil with an inductance of 0.5 H and a resistance of 10 D.
16. If the inductor coil in question 15 is connected across a 120-V source, determine
a. the initial current, in amperes, at the instant the circuit is energized.
b. the current, in amperes, at the end of one time constant after the circuit is energized.
c. the current, in amperes, at the end of two time constants after the circuit is energized.
17. When the inductor coil in question 16 is deenergized, determine the value of the decaying current in amperes
a. at the end of two time constants.
b. at the end of five time constants.
18. a. Explain the difference between a wet and a dry electrolytic capacitor.
b. Where are electrolytic capacitors used?
19. Name four other types of capacitors, in addition to the electrolytic capacitor, that were described in this unit. Briefly describe the material used for the plates and the dielectrics of each type.
20. In schematic wiring diagrams, the curved portion of the symbol for a fixed capaci- tor should be connected in a particular manner. Explain what is meant by this statement.
![clip_image013[1]](http://lh4.ggpht.com/-6mUsrpi5JT4/VK7TT0mG7LI/AAAAAAABC5A/sPFCoqyMSTo/s1600-h/clip_image01312.gif "clip_image013[1]"){kind=small}
