science universe

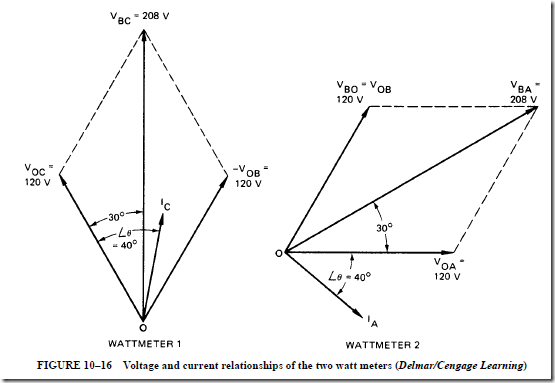
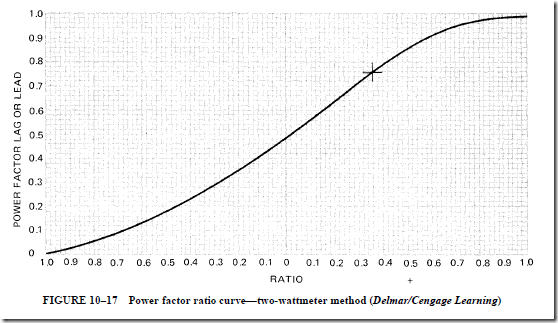
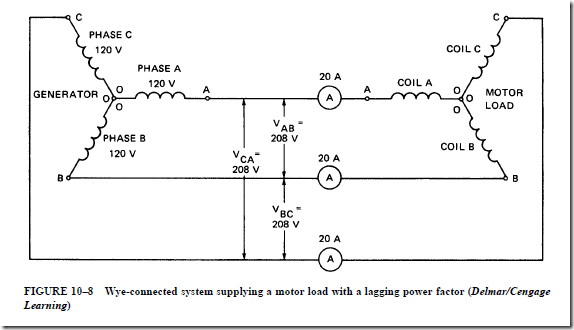
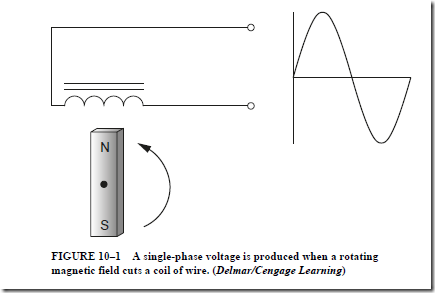
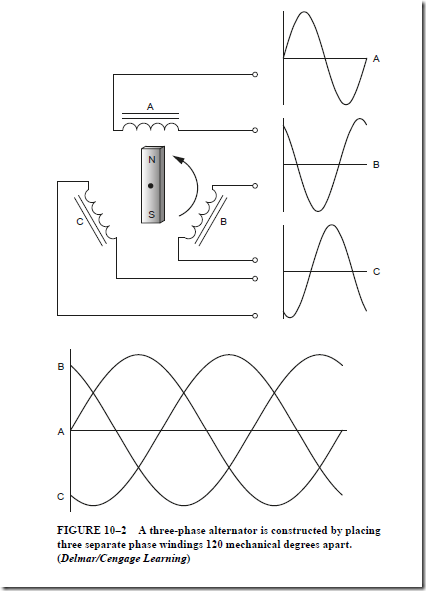
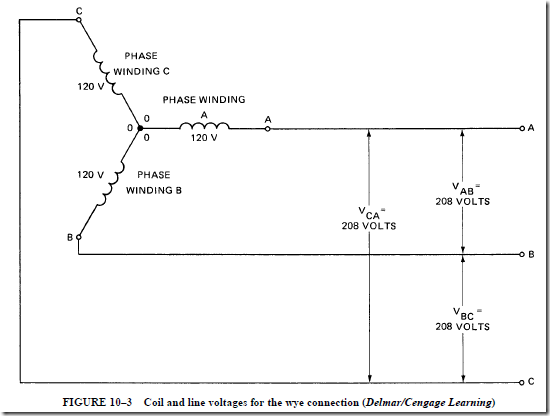
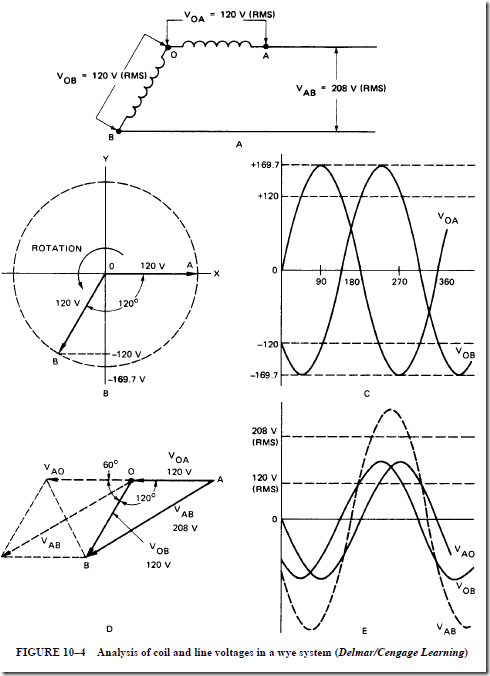
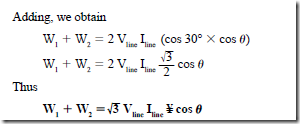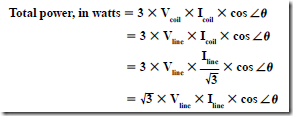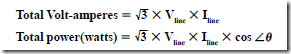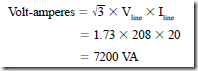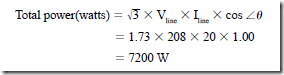AC Instruments and Meters

MEASUREMENT OF AC QUANTITIES

The equipment used to measure ac quantities differs somewhat from the equipment used in dc measurements. This unit will describe the instruments generally used to mea- sure voltage, power factor, VARs, current, watts, frequency, and phase angle. In addition, meters will be described for measuring watt-hours, Watt-hour demand, varhours, and varhour demand.

For the instruments used to measure ac voltage, current, watts, and VARs, each movement must have three basic components:

1. A spring mechanism to produce an opposing torque; the magnitude of this torque depends on the quantity being measured.

2. A restoring spring mechanism to restore the indicator or pointer of the meter to zero after the required measurement is made. In practice, one mechanism is used to pro- duce the opposing torque and then return the indicator to zero.

3. A damping system to prevent the pointer from overshooting and excessive swinging.

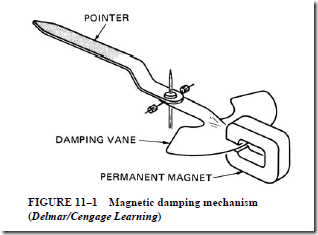
If too much damping is provided, a long time is required before the pointer can reach a new reading after a change occurs in the measured quantity. The proper damping means that the pointer moves quickly and stabilizes quickly when the quantity being measured is changed. AC instruments often use electromagnetic damping. As shown in Figure 11–1, a permanent magnet induces eddy currents in some part of the instrument movement. The magnetic effect of these eddy currents opposes the motion of the pointer. Air damping is another method of controlling the motion of the pointer. In this method, a vane retards the movement of the pointer.

MEASUREMENT OF VOLTAGE AND CURRENT

Alternating current and voltage can be measured using several different types of movements. These movements vary in their ability to meet the criteria expressed in the following questions:

1. Does the instrument scale indicate RMS or average values?

2. To what value of volts or amperes must the movement respond?

3. Is the calibration of the scale linear in the useful range, or are the numbers on the scale crowded together in some important region?

4. How accurate is the instrument?

5. How much does it cost?

RECTIFIER INSTRUMENTS WITH D’ARSONVAL MOVEMENT

Direct Current Fundamentals described the d’Arsonval dc instrument movement. This movement can be used for ac measurement if a rectifier is also used.

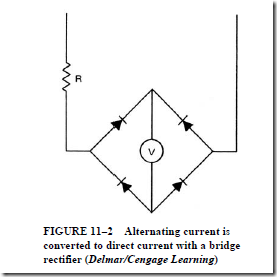
Figure 11–2 shows a bridge-connected full-wave rectifier used with a voltmeter. (R is the series resistor normally required with a voltmeter.)

The dc d’Arsonval movement develops a torque that is proportional to the average value of the current in the moving coil. For an ac wave, only the RMS (effective) values are of interest. Thus, the ac scale is calibrated in RMS values. The RMS voltage is 1.11 times the average voltage value of a sine wave. This means that rectifier-type measuring instruments are accurate only when pure sine-wave quantities are involved. If the voltage to be measured has another type of wave shape, the instrument will give erroneous readings.

Multimeters are instruments that measure both ac and dc quantities. d’Arsonval move- ments are used in most multimeters. When used as a voltmeter, a multimeter is expected to have a high resistance linear scale and consume relatively little power. When used as an ammeter, most rectifier-type multimeters must be used in the range of microamperes or milliamperes. The full-scale readings will range from about 100 µA to 1000 mA. A multi- meter with a d’Arsonval movement is shown in Figure 11–3.

OTHER TYPES OF AC VOLTMETER AND AMMETER MOVEMENTS

Several other types of ac movements can be used in measuring instruments. These movements include the following:

• Magnetic vane attraction movement

• Inclined coil movement

• Repulsion movement

• Repulsion–attraction movement

• Dynamometer movement

All of the movements listed respond to RMS values of voltage or current.

The Magnetic Vane Attraction Movement

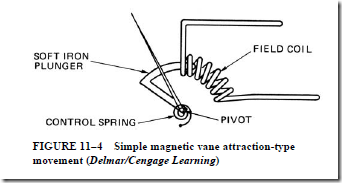
This type of movement has a soft iron plunger that projects into a stationary field coil (Figure 11–4). Current in the field coil produces a magnetic force that pulls the plunger deeper into the coil. The instantaneous value of this magnetic force is proportional to the square of the current in the coil. This means that the average torque turning the movement is proportional to the average, or mean, of the squares of the coil current (the RMS values).

This torque is independent of current direction. Thus, the instrument can be used for either ac or dc measurements.

The magnetic force that attracts the plunger has a minimum value when the plunger is just entering the coil. The value of the force increases rapidly as more of the soft iron vane enters the coil. This means that the numbers are crowded together at the lower end of the scale and are expanded for the high end of the scale. This type of movement is commonly used in low-cost ammeters. When a coil of many turns and a series resistor are added, this movement can be used to make voltage measurements.

Inclined Coil Movement

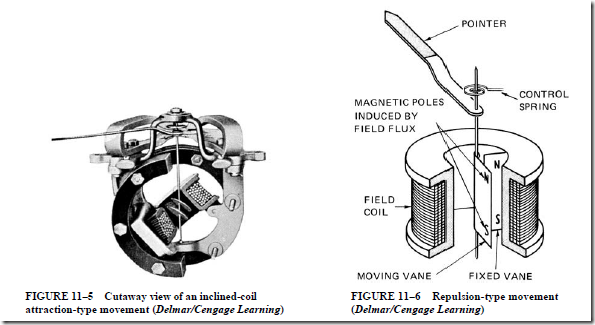
The Thompson inclined coil movement (Figure 11–5) is used in portable and switch- board ammeters and voltmeters. The scale of this movement is long and reasonably linear. An iron vane is free to move in a magnetic field. The vane tends to take a position parallel to the flux. Figure 11–5 shows a pair of elliptical iron vanes attached to a shaft passing through the center of the stationary field coil. If the current in the field coil is increased, an increasing force is produced, which tends to align the vanes with (parallel to) the coil flux. As a result, the shaft turns and moves the attached pointer across the scale.

Repulsion Movement

The repulsion-type movement can be used for both current and voltage measure- ments. A repulsion force is developed between two soft iron vanes that are affected by the same magnetic field (Figure 11–6). One iron vane is attached to the instrument shaft.

The other vane is mounted on the stationary field coil. When there is no current in the coil, the control spring holds the movable vane close to the fixed vane. Alternating current in the field coil magnetizes both vanes. The like poles of the vanes repel each other and create a torque. This torque turns the instrument shaft. The repulsion force between the two vanes varies according to the square of the current. This force also varies inversely as the square of the distance between the vanes. As a result, the movement has a reasonably uniform scale.

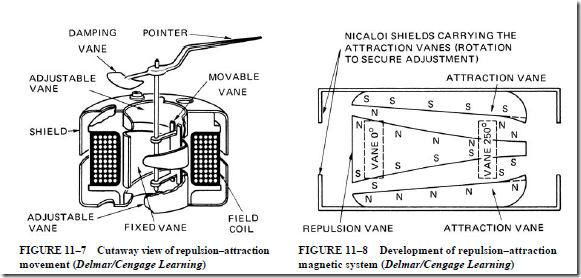
The Repulsion–Attraction Movement (Figure 11–7)

This type of movement is used for both ammeters and voltmeters. It produces more torque per watt than do any of the other ac movements included in this list. A cutaway view of the structure of the repulsion–attraction movement is shown in Figure 11–7.

The instantaneous polarities of the iron vanes are shown in Figure 11–8. The movable vane is repelled from the wide end of the middle fixed vane first. The repelling force decreases as the vane moves to the narrow end of the middle vane. An attracting force increases as the ends of the moving vane come closer to the upper and lower fixed attraction vanes. When these fixed attraction vanes have the correct size and spacing, a scale length representing 250° of angular deflection can be provided. The distribution of values along the scale is determined by the shape and separation of the vanes. Meters can be designed to broaden the scale at any point.

Dynamometer Movement

The dynamometer movement produces a torque by the interaction of magnetic fields. One field is caused by the current in a moving coil. A second field is due to the current in a stationary coil. This stationary magnetic field is not constant. It varies with the amount

of current in the stationary coils. Thus, the torque produced in this movement depends on the moving coil current and the stationary coil current. The fixed and moving coils are connected in series. The dynamometer movement can be adapted easily to make voltage measurements by adding the proper series resistor.

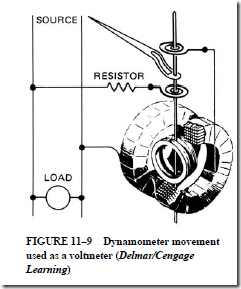
Figure 11–9 shows a dynamometer movement used as a voltmeter. When compared with d’Arsonval movements, the dynamometer movement is more efficient and accurate (to one-quarter of 1% or better). This type of movement is seldom used as an ammeter for the following reasons: (1) the lead-in spirals to the moving coil can carry a limited current only, (2) frequency variations influence the inductance of the coils and introduce error, and

(1) the resistance of the two coils in series may produce an undesirably high voltage drop across the shunt.

The torque is determined by changes in the stationary coil current or the movable coil current. Because of this fact, the dynamometer movement is a very useful measuring device for several other applications. Although this type of movement may be used for dc, most of its practical uses are for ac. For example, instruments with dynamometer movements are used to measure power in watts and reactive volt-amperes. Such instruments are also used to measure power factor and frequency and to indicate synchronism in ac circuits.

THE THREE-WATTMETER METHOD

Many wye-connected systems have a neutral wire in addition to the three line wires. Such a system is called a three-phase, four-wire, wye-connected circuit (Figure 10–18). The neutral wire connects at the common point where the three coil windings terminate in the alternator. The neutral then runs directly to the common point of the wye-connected load. This type of system is used when 120-V, single-phase service is required for lighting loads. In addition, it is used when three-phase, 208-V service is required for three-phase motor loads. The neutral wire helps to maintain relatively constant voltages across the three sections of the wye-connected load when the currents are unbalanced.

For this type of system, the three-wattmeter method is used to measure the power in the circuit.

Connections for the Three-Wattmeter Method

The connections for the three-wattmeter method are shown in Figure 10–18. The current coil of each single-phase wattmeter is connected in series with one of the three line wires. The potential coil of each wattmeter is connected between the line wire to which its current coil is connected and the common neutral wire. Thus, each wattmeter indicates only the power taken by one of the three sections of the wye-connected load. In this type of circuit connection, the wattmeter will never read backward. However, different readings are obtained if the loads are unbalanced. If the currents are balanced and

the voltages are equal, then all three wattmeters will read equal values. According to the three-wattmeter method, the total power taken by a three-phase, four-wire system is

Total watts = W₁ + W₂ + W₃

TWO-PHASE SYSTEM

Two-phase systems are rapidly being replaced by the three-phase system. The reasons for the popularity of three-phase systems were given at the beginning of this unit. How- ever, the student may have to work with a two-phase system at some point. Thus, some basic information about such systems is presented here. Basically, a two-phase generator consists of two single-phase windings placed 90 mechanical degrees apart in the slots of the stator core. The output of this generator consists of two sine waves of voltage 90 electrical degrees apart.

One type of two-phase system is the two-phase, four-wire system (Figure 10–19A). This system consists of two separate single-phase circuits. These circuits are isolated electrically from each other. In the second type of two-phase system (Figure 10–19B), the two phases are interconnected. The result of this arrangement is a two-phase, three-wire system. The voltage across the outside wires of this system is equal to �2 times the coil voltage. It should be evident to the student that this voltage value results because the induced voltages in the phase windings are 90 electrical degrees apart and are of equal magnitude.

SUMMARY

• A three-phase system has the following advantages as compared to a single-phase system:

1. Three-phase generators and motors have a capacity approximately 150% that of single-phase units of the same physical size.

2. Three-phase power is constant and single-phase power is pulsating.

3. Generators, motors, transformers, feeders, and other three-phase devices have a savings in copper of approximately 25% over single-phase devices.

4. Three-phase devices are lower in initial cost and maintenance than are single- phase devices.

• A three-phase circuit consists of three single-phase circuits combined into one circuit having either three or four wires.

• Single-phase motors and other single-phase loads may be operated from a three-phase system.

• A simple three-phase generator consists of three coils or phase windings placed in the slots of the stationary armature (the stator). The windings are placed so that the three induced voltages are 120 electrical degrees apart.

1. The induced voltage in each phase winding is called the phase voltage.

2. The voltage across the line wires is called the line-to-line voltage.

3. Three-phase generators, motors, and transformers can be connected in the wye or delta configuration.

• The phase sequence, or the phase rotation, is the order in which the three voltages of a three-phase circuit follow one another.

1. Counterclockwise rotation of the generator produces the phase sequence ACB. Clockwise rotation produces the phase sequence ABC.

2. The phase sequence may be changed by reversing the direction of rotation of the three-phase generator or by interchanging the connections of any two of the three line wires.

• Wye connection:

1. The wye-connection is the most commonly used way of connecting the three single-phase windings of three-phase generators.

2. A wye connection is made by connecting one end of each phase winding or coil to a common point. The other end of each coil is brought out and connected separately, one to each line lead.

3. If the voltage induced in each phase winding is 120 V, the voltage across each pair of line wires is not equal to 240 V. The two phase voltages are 120° out of phase. The line-to-line voltage will be 208 V:

4. The voltages between phases A and B, B and C, and C and A are all 208 V.

5. The line current and the phase winding current are the same because each phase winding is connected in series with one of the three line wires.

• Kirchhoff’s current law states that

1. the sum of the currents at a junction point in a circuit network is always zero.

2. the sum of the currents leaving a point must equal the sum of the currents entering that point.

• Power in the wye-connected system:

3. It is easier to measure line voltages and line current than it is to find the coil volt-ages and the coil currents (I = I_coil in a wye-connected system). Also

If the current values are severely unbalanced, or the three voltages differ greatly, then the three-phase power factor has almost no meaning.

• Delta connection:

1. This is the second standard connection method by which the three single-phase coil windings of a three-phase generator can be interconnected.

2. The term delta is used because the schematic diagram of this connection closely resembles the uppercase Greek letter delta (.1).

3. The phase and line voltages have common points; thus, these voltages are equal.

4. The three line currents, I , I , and I are 120 electrical degrees apart in a balanced three-phase system:

5. The total volt-amperes for both a balanced three-phase, three-wire, wye-connected system and a balanced three-phase, three-wire, delta-connected system is

6. The total power for both a balanced three-phase, three-wire, wye-connected sys- tem and a balanced three-phase, three-wire, delta-connected system is

7. The power factor of a balanced delta-connected, three-phase system is

If the currents and voltages in a delta system are severely unbalanced, the three- phase power factor has no real significance.

• The power, in watts, taken by a three-phase, three-wire system can be measured with two wattmeters. This method can be used to measure the power in both a three-wire wye system and a three-wire delta system.

1. The current coils of the two wattmeters are connected in series with two of the three line leads.

2. The potential coil of each wattmeter is connected between the line wire connect- ing the current coil and the third line wire.

3. Careful attention must be paid to the polarity marks (±) on the voltage and current coils of the wattmeters.

4.

• Three-wattmeter method:

1. Many wye-connected systems have a neutral wire in addition to the three line wires. This neutral wire is connected between the common point of the coils in the alternator and the common point of the wye-connected load. Such a system is called a three-phase, four-wire, wye-connected circuit.

2. The three-wattmeter method is used to measure the power in this circuit.

a. The current coil of each single-phase wattmeter is connected in series with one of the three line wires.

b. The potential coil of each wattmeter is connected between the line wire to which its current coil is connected and the common neutral wire.

c. Total watts = W₁ + W₂ + W₃.

• Two-phase system:

1. Basically, a two-phase generator has two single-phase windings placed 90 mechanical degrees apart in the slots of the stator core.

2. The two line voltages of a two-phase system are 90 electrical degrees apart.

3. A two-phase, four-wire system consists of two separate single-phase circuits, isolated electrically from each other.

4. In a two-phase, three-wire system, the two single-phase windings are electrically connected at one end of each coil and are brought out as one of the three line wires. The other two line wires each connect to the free end of the phase coil.

a. The voltage across the outside wires of this system is

b. The voltage from either one of the outside wires to the center wire is equal to the coil voltage.

Achievement Review

1. The three windings of a three-phase, 60-Hz ac generator are connected in wye.

Each of the three coil windings is rated at 5000 VA and 120 V. Determine

a. the line voltage.

b. the line current when the generator is delivering its full-load output.

c. the full-load rating of the three-phase generator, in kilovolt-amperes.

2. The three-phase generator in question 1 delivers the rated output to a three-phase noninductive heating load. As a result, the current in each coil of the generator is in phase with its respective voltage.

a. Determine the full-load output of the generator in kilowatts.

b. Draw a vector diagram to scale of the resulting voltages and currents when the three-phase generator delivers the full-load output to this noninductive load. All vectors must be properly labeled.

3. The three-phase generator in question 1 is connected to a balanced three-phase load. This connection causes each coil current of the generator to lag its respective coil voltage by 30°.

a. Determine the output of the alternator, in kilowatts, when the full-load output is delivered to this type of load.

b. Draw a vector diagram to scale of the voltages and currents for the alternator when it delivers the rated output with a phase angle of 30°. All vectors must be properly labeled.

4. Give several reasons why three-phase connections are preferred to single-phase connections for many alternating-current installations.

5. A heating load consists of three noninductive heating elements connected in delta.

Each heating element has a resistance of 24 n. This heating load is supplied by a 240-V, three-phase, three-wire service. Determine

a. the voltage across each heater element.

b. the current in each heater element.

c. the line current.

d. the total power taken by this three-phase load.

6. Draw a vector diagram to scale of the currents and voltages for the circuit of question 5. All vectors must be properly labeled.

7. A three-phase, delta-connected alternator is rated at 720 kVA, 2400 V, 60 Hz. At the rated load, determine

a. the output, in kilowatts, at an 80% lagging power factor.

b. the coil current.

c. the line current.

d. the voltage rating of each of the three windings.

8. A three-phase, wye-connected alternator is rated at 720 kVA, 2400 V, 60 Hz. At the rated load, determine

a. the output, in kilowatts, at an 80% lagging power factor.

b. the full-load line current.

c. the full-load current rating of each of the three windings.

d. the voltage across each phase winding.

9. A 5-kVA, 208-V, three-phase ac generator is connected in wye.

a. Determine

(1) the voltage of each coil of the phase windings.

(2) the coil current at full load.

b. If the phase windings of this alternator are reconnected in delta, what are the new line voltage and the current values at full load?

10. Three coils are connected in delta across a 240-V, three-phase supply. The line cur- rent is 20 A. The total power delivered to the three coils is 6000 watts. Determine

a. the total load, in volt-amperes.

b. the three-phase power factor.

c. the current in each coil and the voltage across each coil.

d. the impedance, in ohms, of each coil.

11. Draw a vector diagram to scale of the voltages and currents for the three-phase, delta-connected circuit in question 10. All vectors must be properly labeled.

12. Using a circuit diagram, show how to obtain the test data required to determine the total power and the total load volt-amperes in a three-phase, three-wire circuit. (Assume that two single-phase wattmeters, three ammeters, and one voltmeter are to be used to determine the data.)

13. The following test data were obtained for a three-phase, 220-V, 5-hp motor operating at full load:

At full load, determine

a. the power taken by the three-phase motor.

b. the power factor.

14. The following data were obtained by a technician for a 10-hp, 220-V, three-phase motor delivering the rated load output:

At the rated load, determine

a. the input volt-amperes.

b. the power input.

c. the power factor.

d. the efficiency of the motor.

15. Using the curve given in Figure 10–17, determine

a. the power factor of the motor in question 13.

b. the power factor of the motor in question 14.

16. The power input to a three-phase motor is measured by the two-wattmeter method.

The three line voltages are 220 V and the current in each of the three line wires is 8 A. If the three-phase power factor is 0.866 lag, what are the values of power indicated by wattmeter 1 and wattmeter 2?

17. Using the two-wattmeter method, the following test data were obtained for a 440-V, three-phase motor:

a. Determine

(1) the power input to the motor.

(2) the input in volt-amperes.

(3) the power factor.

b. Using the curve given in Figure 10–17, check the power factor obtained in step a(3) of this question.

18. Show the connections for the three-wattmeter method used with a three-phase, four-wire, wye-connected system. Both 120-V, single-phase service and 208-V, three-phase service are to be available.

19. A three-phase, four-wire, wye-connected system supplies a noninductive lighting load only. The current in line A is 8 A, in line B the current is 10 A, and in line C the current is 6 A. The voltage from each line wire to the neutral wire is 120 V.

Determine

a. the power, in watts, indicated by each of the three wattmeters.

b. the total power, in watts, taken by the entire lighting load.

20. With the aid of diagrams, explain the difference between a two-phase, four-wire system and a two-phase, three-wire system.

THE THREE-WATTMETER METHOD

Many wye-connected systems have a neutral wire in addition to the three line wires. Such a system is called a three-phase, four-wire, wye-connected circuit (Figure 10–18). The neutral wire connects at the common point where the three coil windings terminate in the alternator. The neutral then runs directly to the common point of the wye-connected load. This type of system is used when 120-V, single-phase service is required for lighting loads. In addition, it is used when three-phase, 208-V service is required for three-phase motor loads. The neutral wire helps to maintain relatively constant voltages across the three sections of the wye-connected load when the currents are unbalanced.

For this type of system, the three-wattmeter method is used to measure the power in the circuit.

Connections for the Three-Wattmeter Method

The connections for the three-wattmeter method are shown in Figure 10–18. The current coil of each single-phase wattmeter is connected in series with one of the three line wires. The potential coil of each wattmeter is connected between the line wire to which its current coil is connected and the common neutral wire. Thus, each wattmeter indicates only the power taken by one of the three sections of the wye-connected load. In this type of circuit connection, the wattmeter will never read backward. However, different readings are obtained if the loads are unbalanced. If the currents are balanced and

the voltages are equal, then all three wattmeters will read equal values. According to the three-wattmeter method, the total power taken by a three-phase, four-wire system is

Total watts = W₁ + W₂ + W₃

TWO-PHASE SYSTEM

Two-phase systems are rapidly being replaced by the three-phase system. The reasons for the popularity of three-phase systems were given at the beginning of this unit. How- ever, the student may have to work with a two-phase system at some point. Thus, some basic information about such systems is presented here. Basically, a two-phase generator consists of two single-phase windings placed 90 mechanical degrees apart in the slots of the stator core. The output of this generator consists of two sine waves of voltage 90 electrical degrees apart.

One type of two-phase system is the two-phase, four-wire system (Figure 10–19A). This system consists of two separate single-phase circuits. These circuits are isolated electrically from each other. In the second type of two-phase system (Figure 10–19B), the two phases are interconnected. The result of this arrangement is a two-phase, three-wire system. The voltage across the outside wires of this system is equal to �2 times the coil voltage. It should be evident to the student that this voltage value results because the induced voltages in the phase windings are 90 electrical degrees apart and are of equal magnitude.

SUMMARY

• A three-phase system has the following advantages as compared to a single-phase system:

1. Three-phase generators and motors have a capacity approximately 150% that of single-phase units of the same physical size.

2. Three-phase power is constant and single-phase power is pulsating.

3. Generators, motors, transformers, feeders, and other three-phase devices have a savings in copper of approximately 25% over single-phase devices.

4. Three-phase devices are lower in initial cost and maintenance than are single- phase devices.

• A three-phase circuit consists of three single-phase circuits combined into one circuit having either three or four wires.

• Single-phase motors and other single-phase loads may be operated from a three-phase system.

• A simple three-phase generator consists of three coils or phase windings placed in the slots of the stationary armature (the stator). The windings are placed so that the three induced voltages are 120 electrical degrees apart.

1. The induced voltage in each phase winding is called the phase voltage.

2. The voltage across the line wires is called the line-to-line voltage.

3. Three-phase generators, motors, and transformers can be connected in the wye or delta configuration.

• The phase sequence, or the phase rotation, is the order in which the three voltages of a three-phase circuit follow one another.

1. Counterclockwise rotation of the generator produces the phase sequence ACB. Clockwise rotation produces the phase sequence ABC.

2. The phase sequence may be changed by reversing the direction of rotation of the three-phase generator or by interchanging the connections of any two of the three line wires.

• Wye connection:

1. The wye-connection is the most commonly used way of connecting the three single-phase windings of three-phase generators.

2. A wye connection is made by connecting one end of each phase winding or coil to a common point. The other end of each coil is brought out and connected separately, one to each line lead.

3. If the voltage induced in each phase winding is 120 V, the voltage across each pair of line wires is not equal to 240 V. The two phase voltages are 120° out of phase. The line-to-line voltage will be 208 V:

4. The voltages between phases A and B, B and C, and C and A are all 208 V.

5. The line current and the phase winding current are the same because each phase winding is connected in series with one of the three line wires.

• Kirchhoff’s current law states that

1. the sum of the currents at a junction point in a circuit network is always zero.

2. the sum of the currents leaving a point must equal the sum of the currents entering that point.

• Power in the wye-connected system:

3. It is easier to measure line voltages and line current than it is to find the coil volt-ages and the coil currents (I = I_coil in a wye-connected system). Also

If the current values are severely unbalanced, or the three voltages differ greatly, then the three-phase power factor has almost no meaning.

• Delta connection:

1. This is the second standard connection method by which the three single-phase coil windings of a three-phase generator can be interconnected.

2. The term delta is used because the schematic diagram of this connection closely resembles the uppercase Greek letter delta (.1).

3. The phase and line voltages have common points; thus, these voltages are equal.

4. The three line currents, I , I , and I are 120 electrical degrees apart in a balanced three-phase system:

5. The total volt-amperes for both a balanced three-phase, three-wire, wye-connected system and a balanced three-phase, three-wire, delta-connected system is

6. The total power for both a balanced three-phase, three-wire, wye-connected sys- tem and a balanced three-phase, three-wire, delta-connected system is

7. The power factor of a balanced delta-connected, three-phase system is

If the currents and voltages in a delta system are severely unbalanced, the three- phase power factor has no real significance.

• The power, in watts, taken by a three-phase, three-wire system can be measured with two wattmeters. This method can be used to measure the power in both a three-wire wye system and a three-wire delta system.

1. The current coils of the two wattmeters are connected in series with two of the three line leads.

2. The potential coil of each wattmeter is connected between the line wire connect- ing the current coil and the third line wire.

3. Careful attention must be paid to the polarity marks (±) on the voltage and current coils of the wattmeters.

4.

• Three-wattmeter method:

1. Many wye-connected systems have a neutral wire in addition to the three line wires. This neutral wire is connected between the common point of the coils in the alternator and the common point of the wye-connected load. Such a system is called a three-phase, four-wire, wye-connected circuit.

2. The three-wattmeter method is used to measure the power in this circuit.

a. The current coil of each single-phase wattmeter is connected in series with one of the three line wires.

b. The potential coil of each wattmeter is connected between the line wire to which its current coil is connected and the common neutral wire.

c. Total watts = W₁ + W₂ + W₃.

• Two-phase system:

1. Basically, a two-phase generator has two single-phase windings placed 90 mechanical degrees apart in the slots of the stator core.

2. The two line voltages of a two-phase system are 90 electrical degrees apart.

3. A two-phase, four-wire system consists of two separate single-phase circuits, isolated electrically from each other.

4. In a two-phase, three-wire system, the two single-phase windings are electrically connected at one end of each coil and are brought out as one of the three line wires. The other two line wires each connect to the free end of the phase coil.

a. The voltage across the outside wires of this system is

b. The voltage from either one of the outside wires to the center wire is equal to the coil voltage.

Achievement Review

1. The three windings of a three-phase, 60-Hz ac generator are connected in wye.

Each of the three coil windings is rated at 5000 VA and 120 V. Determine

a. the line voltage.

b. the line current when the generator is delivering its full-load output.

c. the full-load rating of the three-phase generator, in kilovolt-amperes.

2. The three-phase generator in question 1 delivers the rated output to a three-phase noninductive heating load. As a result, the current in each coil of the generator is in phase with its respective voltage.

a. Determine the full-load output of the generator in kilowatts.

b. Draw a vector diagram to scale of the resulting voltages and currents when the three-phase generator delivers the full-load output to this noninductive load. All vectors must be properly labeled.

3. The three-phase generator in question 1 is connected to a balanced three-phase load. This connection causes each coil current of the generator to lag its respective coil voltage by 30°.

a. Determine the output of the alternator, in kilowatts, when the full-load output is delivered to this type of load.

b. Draw a vector diagram to scale of the voltages and currents for the alternator when it delivers the rated output with a phase angle of 30°. All vectors must be properly labeled.

4. Give several reasons why three-phase connections are preferred to single-phase connections for many alternating-current installations.

5. A heating load consists of three noninductive heating elements connected in delta.

Each heating element has a resistance of 24 n. This heating load is supplied by a 240-V, three-phase, three-wire service. Determine

a. the voltage across each heater element.

b. the current in each heater element.

c. the line current.

d. the total power taken by this three-phase load.

6. Draw a vector diagram to scale of the currents and voltages for the circuit of question 5. All vectors must be properly labeled.

7. A three-phase, delta-connected alternator is rated at 720 kVA, 2400 V, 60 Hz. At the rated load, determine

a. the output, in kilowatts, at an 80% lagging power factor.

b. the coil current.

c. the line current.

d. the voltage rating of each of the three windings.

8. A three-phase, wye-connected alternator is rated at 720 kVA, 2400 V, 60 Hz. At the rated load, determine

a. the output, in kilowatts, at an 80% lagging power factor.

b. the full-load line current.

c. the full-load current rating of each of the three windings.

d. the voltage across each phase winding.

9. A 5-kVA, 208-V, three-phase ac generator is connected in wye.

a. Determine

(1) the voltage of each coil of the phase windings.

(2) the coil current at full load.

b. If the phase windings of this alternator are reconnected in delta, what are the new line voltage and the current values at full load?

10. Three coils are connected in delta across a 240-V, three-phase supply. The line cur- rent is 20 A. The total power delivered to the three coils is 6000 watts. Determine

a. the total load, in volt-amperes.

b. the three-phase power factor.

c. the current in each coil and the voltage across each coil.

d. the impedance, in ohms, of each coil.

11. Draw a vector diagram to scale of the voltages and currents for the three-phase, delta-connected circuit in question 10. All vectors must be properly labeled.

12. Using a circuit diagram, show how to obtain the test data required to determine the total power and the total load volt-amperes in a three-phase, three-wire circuit. (Assume that two single-phase wattmeters, three ammeters, and one voltmeter are to be used to determine the data.)

13. The following test data were obtained for a three-phase, 220-V, 5-hp motor operating at full load:

At full load, determine

a. the power taken by the three-phase motor.

b. the power factor.

14. The following data were obtained by a technician for a 10-hp, 220-V, three-phase motor delivering the rated load output:

At the rated load, determine

a. the input volt-amperes.

b. the power input.

c. the power factor.

d. the efficiency of the motor.

15. Using the curve given in Figure 10–17, determine

a. the power factor of the motor in question 13.

b. the power factor of the motor in question 14.

16. The power input to a three-phase motor is measured by the two-wattmeter method.

The three line voltages are 220 V and the current in each of the three line wires is 8 A. If the three-phase power factor is 0.866 lag, what are the values of power indicated by wattmeter 1 and wattmeter 2?

17. Using the two-wattmeter method, the following test data were obtained for a 440-V, three-phase motor:

a. Determine

(1) the power input to the motor.

(2) the input in volt-amperes.

(3) the power factor.

b. Using the curve given in Figure 10–17, check the power factor obtained in step a(3) of this question.

18. Show the connections for the three-wattmeter method used with a three-phase, four-wire, wye-connected system. Both 120-V, single-phase service and 208-V, three-phase service are to be available.

19. A three-phase, four-wire, wye-connected system supplies a noninductive lighting load only. The current in line A is 8 A, in line B the current is 10 A, and in line C the current is 6 A. The voltage from each line wire to the neutral wire is 120 V.

Determine

a. the power, in watts, indicated by each of the three wattmeters.

b. the total power, in watts, taken by the entire lighting load.

20. With the aid of diagrams, explain the difference between a two-phase, four-wire system and a two-phase, three-wire system.

POWER MEASUREMENT IN THREE-PHASE SYSTEMS

The power, in watts, taken by a three-phase, three-wire system can be measured with two wattmeters. This method can be used to measure the power in a three-wire wye system or in a three-wire delta system.

The Two-Wattmeter Method

Figure 10–14 shows the standard connections for the two-wattmeter method. In this case, the method is used to measure the power supplied by a three-phase, three-wire system to a wye-connected load. The current coils of the two wattmeters are connected in series with two of the three line leads. The potential coil of each wattmeter is connected between the line wire from the current coil to the third line wire.

Careful attention must be paid to the polarity marks (±) on the voltage and current coils of the wattmeters. The connections must be made exactly as shown in Figure 10–14. The total power for the three-phase system is

P_T = W₁+ W₂

The ± side of the voltage coil of W2 is connected to line A. The other side of this coil is connected to line B. As a result, the voltage coil of the wattmeter reads the voltage at A with respect to B, or V 

Similarly, the voltage coil of W reads V  . Figure 10–15 shows the construction of these voltage vectors for a unity power factor.

A wattmeter will read the product of V and I line multiplied by the cosine of the angle between the two values. Recall, however, that the power factor for a three-phase system is measured between V and I  . The following two examples illustrate the use of the two- wattmeter method of determining the power.

Case I: Unity Power Factor. At a power factor of unity, the angle between V_line  and I  is 30°, as shown in Figure 10–15:

5. At 0 > 60°, W2 is the negative and W1 is positive. In the case of 8 > 60°, W2 is negative. Thus, it is necessary to reverse the voltage coil connections of wattmeter 2 so that it reads upscale. The reading must be recorded as a negative value and must be subtracted from W to obtain the total power:

These formulas are also correct for a balanced three-phase, delta-connected load.

Using the curve shown in Figure 10–17, it is possible to obtain the power factor with- out finding the input volt-amperes. Power factor values form the vertical scale. The ratios of the smaller wattmeter reading to the larger reading form the horizontal scale. The curve in Figure 10–17 is obtain by substituting different values of the angle 8 in the following ratio:

When applied to the curve of Figure 10–17, this ratio gives a power factor of 0.76. As another example, wattmeter 1 has a phase angle of 75° lagging and a power factor of 0.2588. Wattmeter 1 reads 1471 W and wattmeter 2 reads -538 W. The ratio of these two values is W2÷  W1 = -538 ÷ 1471 = -0.36. When applied to the curve, the  ratio gives a power factor of 0.26 lagging. This reading is close to the given value  of 0.2588.

POWER MEASUREMENT IN THREE-PHASE SYSTEMS

The power, in watts, taken by a three-phase, three-wire system can be measured with two wattmeters. This method can be used to measure the power in a three-wire wye system or in a three-wire delta system.

The Two-Wattmeter Method

Figure 10–14 shows the standard connections for the two-wattmeter method. In this case, the method is used to measure the power supplied by a three-phase, three-wire system to a wye-connected load. The current coils of the two wattmeters are connected in series with two of the three line leads. The potential coil of each wattmeter is connected between the line wire from the current coil to the third line wire.

Careful attention must be paid to the polarity marks (±) on the voltage and current coils of the wattmeters. The connections must be made exactly as shown in Figure 10–14. The total power for the three-phase system is

P_T = W₁+ W₂

The ± side of the voltage coil of W2 is connected to line A. The other side of this coil is connected to line B. As a result, the voltage coil of the wattmeter reads the voltage at A with respect to B, or V 

Similarly, the voltage coil of W reads V  . Figure 10–15 shows the construction of these voltage vectors for a unity power factor.

A wattmeter will read the product of V and I line multiplied by the cosine of the angle between the two values. Recall, however, that the power factor for a three-phase system is measured between V and I  . The following two examples illustrate the use of the two- wattmeter method of determining the power.

Case I: Unity Power Factor. At a power factor of unity, the angle between V_line  and I  is 30°, as shown in Figure 10–15:

5. At 0 > 60°, W2 is the negative and W1 is positive. In the case of 8 > 60°, W2 is negative. Thus, it is necessary to reverse the voltage coil connections of wattmeter 2 so that it reads upscale. The reading must be recorded as a negative value and must be subtracted from W to obtain the total power:

These formulas are also correct for a balanced three-phase, delta-connected load.

Using the curve shown in Figure 10–17, it is possible to obtain the power factor with- out finding the input volt-amperes. Power factor values form the vertical scale. The ratios of the smaller wattmeter reading to the larger reading form the horizontal scale. The curve in Figure 10–17 is obtain by substituting different values of the angle 8 in the following ratio:

When applied to the curve of Figure 10–17, this ratio gives a power factor of 0.76. As another example, wattmeter 1 has a phase angle of 75° lagging and a power factor of 0.2588. Wattmeter 1 reads 1471 W and wattmeter 2 reads -538 W. The ratio of these two values is W2÷  W1 = -538 ÷ 1471 = -0.36. When applied to the curve, the  ratio gives a power factor of 0.26 lagging. This reading is close to the given value  of 0.2588.

POWER IN THE WYE SYSTEM

The value of volt-amperes produced in each of the three single-phase windings of the three-phase generator is

Volt-amperes = V_coil X I_coil

If the voltage and current values of the wye system are balanced, the total volt-amperes produced by all three windings is

Total Volt-amperes = 3 X V_coil X I_coil

Each of the three coil windings of the wye-connected generator supplies power, in watts, equal to

Three-Phase Power

The total three-phase power, in watts, can be determined for these conditions:

1. The three coil currents are the same.

2. The three coil voltages are equal.

3. The power factor angle is the same for each coil winding.

The equations used to determine the total three-phase power are

Power Factor

The power factor of a balanced three-phase wye-connected system can be deter- mined when the total power (true power or watts) and the total input (apparent power or volt-amperes) are given. The equation expressing the relationship is

In a balanced three-phase circuit, the power factor is always the cosine of the angle between the coil voltage and the coil current. If the current values are severely unbalanced, or if the three voltages differ greatly, then the three-phase power factor has almost no meaning. When the unbalance is minor, then average values of the line current and the line voltage are used in the power factor formula.

THE DELTA CONNECTION

There is a second standard connection method by which the three single-phase coil windings of a three-phase generator can be interconnected. This second method is called the delta connection. Loads connected to a three-phase system may be connected in delta. The name delta is used because the schematic diagram of this connection closely resembles the Greek letter delta (.1).

The schematic diagram of a delta connection is shown in Figure 10–10. This figure represents a three-phase generator consisting of three coil windings. The end of each winding is identified by the letter O. The beginning of each phase winding is marked with the letter A, B, or C.

Making the Delta Connection

The delta connection is made by connecting the beginnings of the coil windings as follows: coil winding A to the end of coil winding B and to line A, coil winding B to the end of coil winding C and to line B, and coil winding C to the end of coil winding A and to line C, as in Figure 10–10.

Figure 10–10 shows line voltage V_AB connected across phase winding B at points OA and OB. Line voltages V and V are then connected across phase windings C and A, respectively. The phase and line voltages have common points; thus, these voltages must be equal.

Adding Coil Currents. The coil currents for the circuit of Figure 10–12 must be added using a method similar to that used in Figure 10–4. Using the vector triangle, it can be shown that

For Figure 10–12A, it is assumed that the current in each phase winding is 10 A. The load consists of three noninductive heater units connected in delta. Each heater unit has a resistance of 24 n. If the line-to-line voltage is 240 V, the voltage across each heater unit is also 240 V. The current in each load resistance is

This means that the current in each of the three coil windings of the three-phase generator and in each load resistor is 10 A. The coil current is in phase with the coil voltage in each phase winding because the load consists of noninductive resistance.

Lagging Power Factor

A three-phase balanced system connected in delta will have a lagging power fac- tor if the system supplies an inductive load, such as an induction motor. Figure 10–13 shows a three-phase generator connected in delta supplying a three-phase motor, also connected in delta. Figure 10–13A is the schematic diagram of this system. The vec- tor diagram for the circuit is shown in Figure 10–13B. If the coil current lags the coil voltage by 40°, the power factor is 0.766 lagging. (The power factor equals the cosine of 40°, or 0.766.) The line current is a vector sum and is equal to 1.73 times the coil current.

Relationships between the Currents and Voltages

The relationships between the phase winding and the line values of the current and voltage for a balanced three-phase delta system are as follows:

• The phase winding voltage and the line voltage values are equal.

• The line current is equal to the �3, or 1.73, times the phase winding current.

POWER IN THE DELTA SYSTEM

The value of volt-amperes supplied by each phase winding of a three-phase generator is

Volt-amperes = V_coil X I_coil

If the voltages and currents of a delta-connected system are balanced, the total volt- amperes of all three windings is

Total VA = 3 X V_coil X I_coil

It is easier to measure the line voltage and the line current than it is to measure coil values. Therefore, the equation for the total volt-amperes of a balanced three-phase delta system is rewritten using the line voltage and the line current values. The line voltage may be substituted for the coil voltage because they are the same in a delta system. Thus, the equation becomes

Total VA = 3 X V_line X I_coil

The equation for the total three-phase power, in watts, can be written if it is assumed that the three coil voltages are equal, the three coil currents are the same, and the power factor angle is the same for each coil. Thus,

The total volt-amperes and the total power for the balanced three-phase wye system and the balanced three-phase delta system are expressed by the same equations:

The power factor of a balanced delta-connected, three-phase system is the ratio of the total power (in watts) to the total volt-amperes:

If the currents and voltages in a delta system are severely unbalanced, the three-phase power factor has no real significance.

PROBLEM 1

Statement of the Problem

The wye-connected, three-phase generator shown in Figure 10–6 supplies power to a three-phase noninductive load. Determine

1. the line voltage.

2. the line current.

3. the input volt-amperes.

4. the power, in watts.

Solution

1. In a three-phase wye system, the line voltage is equal to �3 times the phase winding

voltage:

2. The line current equals the phase winding current. Each heater unit has a resistance of 6 n. If the voltage across each resistor is 120 V, then the coil current is I = V –: R = 120 –: 6 = 20 A. This value is the coil current at both the load and the source. Because each phase winding is in series with a line wire and a load element, the line current is also 20 A.

3. The value of the input volt-amperes is

4. The power factor is unity. This means that the power, in watts, is equal to the value of volt-amperes. The phase angle is zero because the coil current and the voltage are in phase for a noninductive heating load. The true power is

PROBLEM 2

Statement of the Problem

A wye-connected, three-phase generator is shown in Figure 10–8. This generator supplies a motor load. The power factor angle is 40° lagging. Determine

1. the value of the input volt-amperes.

2. the true power, in watts.

Solution

PROBLEM 3

Statement of the Problem

A three-phase alternator is connected in wye. Each phase winding is rated at 8000 V and 418 A. The alternator is designed to operate at a full-load output with a power factor of 80% lag. Determine

1. the line voltage.

2. the line current.

3. the full load volt-ampere rating, in kilovolt-amperes.

4. the full load power, in kilowatts.

Solution

PROBLEM 4

Statement of the Problem

The delta-connected generator shown in Figure 10–13 supplies a delta-connected induction motor. The three-phase power factor of the motor is 0.7660 lagging. Find

1. the line voltage.

2. the line current.

3. the apparent power input to the motor, in volt-amperes.

4. the true power input to the motor, in watts.

Solution

1. For a circuit connected in delta, the line voltage and the coil voltage are the same:

POWER IN THE WYE SYSTEM

The value of volt-amperes produced in each of the three single-phase windings of the three-phase generator is

Volt-amperes = V_coil X I_coil

If the voltage and current values of the wye system are balanced, the total volt-amperes produced by all three windings is

Total Volt-amperes = 3 X V_coil X I_coil

Each of the three coil windings of the wye-connected generator supplies power, in watts, equal to

Three-Phase Power

The total three-phase power, in watts, can be determined for these conditions:

1. The three coil currents are the same.

2. The three coil voltages are equal.

3. The power factor angle is the same for each coil winding.

The equations used to determine the total three-phase power are

Power Factor

The power factor of a balanced three-phase wye-connected system can be deter- mined when the total power (true power or watts) and the total input (apparent power or volt-amperes) are given. The equation expressing the relationship is

In a balanced three-phase circuit, the power factor is always the cosine of the angle between the coil voltage and the coil current. If the current values are severely unbalanced, or if the three voltages differ greatly, then the three-phase power factor has almost no meaning. When the unbalance is minor, then average values of the line current and the line voltage are used in the power factor formula.

THE DELTA CONNECTION

There is a second standard connection method by which the three single-phase coil windings of a three-phase generator can be interconnected. This second method is called the delta connection. Loads connected to a three-phase system may be connected in delta. The name delta is used because the schematic diagram of this connection closely resembles the Greek letter delta (.1).

The schematic diagram of a delta connection is shown in Figure 10–10. This figure represents a three-phase generator consisting of three coil windings. The end of each winding is identified by the letter O. The beginning of each phase winding is marked with the letter A, B, or C.

Making the Delta Connection

The delta connection is made by connecting the beginnings of the coil windings as follows: coil winding A to the end of coil winding B and to line A, coil winding B to the end of coil winding C and to line B, and coil winding C to the end of coil winding A and to line C, as in Figure 10–10.

Figure 10–10 shows line voltage V_AB connected across phase winding B at points OA and OB. Line voltages V and V are then connected across phase windings C and A, respectively. The phase and line voltages have common points; thus, these voltages must be equal.

Adding Coil Currents. The coil currents for the circuit of Figure 10–12 must be added using a method similar to that used in Figure 10–4. Using the vector triangle, it can be shown that

For Figure 10–12A, it is assumed that the current in each phase winding is 10 A. The load consists of three noninductive heater units connected in delta. Each heater unit has a resistance of 24 n. If the line-to-line voltage is 240 V, the voltage across each heater unit is also 240 V. The current in each load resistance is

This means that the current in each of the three coil windings of the three-phase generator and in each load resistor is 10 A. The coil current is in phase with the coil voltage in each phase winding because the load consists of noninductive resistance.

Lagging Power Factor

A three-phase balanced system connected in delta will have a lagging power fac- tor if the system supplies an inductive load, such as an induction motor. Figure 10–13 shows a three-phase generator connected in delta supplying a three-phase motor, also connected in delta. Figure 10–13A is the schematic diagram of this system. The vec- tor diagram for the circuit is shown in Figure 10–13B. If the coil current lags the coil voltage by 40°, the power factor is 0.766 lagging. (The power factor equals the cosine of 40°, or 0.766.) The line current is a vector sum and is equal to 1.73 times the coil current.

Relationships between the Currents and Voltages

The relationships between the phase winding and the line values of the current and voltage for a balanced three-phase delta system are as follows:

• The phase winding voltage and the line voltage values are equal.

• The line current is equal to the �3, or 1.73, times the phase winding current.

POWER IN THE DELTA SYSTEM

The value of volt-amperes supplied by each phase winding of a three-phase generator is

Volt-amperes = V_coil X I_coil

If the voltages and currents of a delta-connected system are balanced, the total volt- amperes of all three windings is

Total VA = 3 X V_coil X I_coil

It is easier to measure the line voltage and the line current than it is to measure coil values. Therefore, the equation for the total volt-amperes of a balanced three-phase delta system is rewritten using the line voltage and the line current values. The line voltage may be substituted for the coil voltage because they are the same in a delta system. Thus, the equation becomes

Total VA = 3 X V_line X I_coil

The equation for the total three-phase power, in watts, can be written if it is assumed that the three coil voltages are equal, the three coil currents are the same, and the power factor angle is the same for each coil. Thus,

The total volt-amperes and the total power for the balanced three-phase wye system and the balanced three-phase delta system are expressed by the same equations:

The power factor of a balanced delta-connected, three-phase system is the ratio of the total power (in watts) to the total volt-amperes:

If the currents and voltages in a delta system are severely unbalanced, the three-phase power factor has no real significance.

PROBLEM 1

Statement of the Problem

The wye-connected, three-phase generator shown in Figure 10–6 supplies power to a three-phase noninductive load. Determine

1. the line voltage.

2. the line current.

3. the input volt-amperes.

4. the power, in watts.

Solution

1. In a three-phase wye system, the line voltage is equal to �3 times the phase winding

voltage:

2. The line current equals the phase winding current. Each heater unit has a resistance of 6 n. If the voltage across each resistor is 120 V, then the coil current is I = V –: R = 120 –: 6 = 20 A. This value is the coil current at both the load and the source. Because each phase winding is in series with a line wire and a load element, the line current is also 20 A.

3. The value of the input volt-amperes is

4. The power factor is unity. This means that the power, in watts, is equal to the value of volt-amperes. The phase angle is zero because the coil current and the voltage are in phase for a noninductive heating load. The true power is

PROBLEM 2

Statement of the Problem

A wye-connected, three-phase generator is shown in Figure 10–8. This generator supplies a motor load. The power factor angle is 40° lagging. Determine

1. the value of the input volt-amperes.

2. the true power, in watts.

Solution

PROBLEM 3

Statement of the Problem

A three-phase alternator is connected in wye. Each phase winding is rated at 8000 V and 418 A. The alternator is designed to operate at a full-load output with a power factor of 80% lag. Determine

1. the line voltage.

2. the line current.

3. the full load volt-ampere rating, in kilovolt-amperes.

4. the full load power, in kilowatts.

Solution

PROBLEM 4

Statement of the Problem

The delta-connected generator shown in Figure 10–13 supplies a delta-connected induction motor. The three-phase power factor of the motor is 0.7660 lagging. Find

1. the line voltage.

2. the line current.

3. the apparent power input to the motor, in volt-amperes.

4. the true power input to the motor, in watts.

Solution

1. For a circuit connected in delta, the line voltage and the coil voltage are the same:

PARALLEL CIRCUIT WITH BRANCHES CONTAINING R AND X_C

Another type of parallel circuit is shown in Figure 8–6. In this circuit, two branches contain noninductive resistance loads and a third branch contains a capacitor. Assuming that the capacitor has negligible resistance, the current in the capacitive branch leads the line voltage by 90 electrical degrees. This means that the line current is the vector sum of the currents in the branches.

PROBLEM 3

Statement of the Problem

The circuit shown in Figure 8–6 contains noninductive resistance and capacitance. For this circuit:

1. Find the current taken by each branch.

2. Construct a vector diagram.

3. Find the total or line current.

4. Find the power taken by the parallel circuit.

5. Find the power factor for the parallel circuit.

6. Find the phase angle.

7. Find the combined impedance.

Solution

1. Branches 1 and 2 contain pure resistance only. The current in each of these branches is in phase with the line voltage.

The total in-phase current for the parallel circuit is the sum of the currents in the first two branches: 8 + 4 = 12 A. The quadrature (out-of-phase) component of current is supplied to the capacitor load in branch 3. This current leads the line voltage by 90° and is given by

2. The vector diagram for the circuit is given in Figure 8–7. The two in-phase current values are placed on the line voltage vector. The total in-phase current is 12 A. The current in the capacitive branch is drawn on the vector diagram in a vertical direction from point 0. Thus, the quadrature current leads the line voltage by 90°. The line current is the vector sum of the total in-phase current and the leading quadrature cur- rent. Note that the line current leads the line voltage by the angle fJ. As a result, this parallel circuit operates with a leading power factor.

3. The line current is the hypotenuse of the right triangle shown in Figure 8–7:

6. The line current leads the line voltage by a phase angle (fJ) of 22.6°.

7. The combined impedance (in ohms) of the parallel circuit is

Another formula that can be used to determine the impedance in a circuit that contains both resistance and capacitive reactance connected in parallel is

PARALLEL CIRCUIT WITH BRANCHES CONTAINING R AND Z_coil

The parallel circuit shown in Figure 8–8 contains two branches. One branch contains a pure resistance of 30 n. The second branch contains a load that has both resistance and inductance. This load is similar to a motor or transformer. The symbol Z_coil is used instead of X because of the coil resistance. It should be noted, however, that the value of Z_coil applies only to the impedance of the coil and should not be confused with the value for the total impedance of the circuit, which is Z total In this circuit, a wattmeter is used to measure the true power of the circuit, and ammeters are used to measure the total current flow and the current flow through each branch. In this circuit, the current will lag the voltage by some value less than 90°.

PROBLEM 4

Statement of the Problem

For the circuit in Figure 8–8, the following items are to be determined:

1. The current taken by each branch

2. The resistance of the coil

3. The power factor of the coil

4. The in-phase component of current in the coil

5. The quadrature component of current in the coil

6. Total impedance of the circuit

Draw a vector diagram for the circuit, and determine (1) the line current and (2) the circuit power factor.

Solution

1. The current in each branch of the circuit is given by Ohm’s law:

The true power taken by the resistance branch is subtracted from the total power taken by the parallel circuit to find the power taken by the coil. Thus, the actual power used in this coil is coil = 624 – 480 = 144 W Therefore, the resistance of the coil is

3. To find the power factor of the coil, it is assumed that the coil is a series circuit containing resistance and inductive reactance. For this case, the power factor is expressed as follows:

For a power factor of 0.20, the coil current lags behind the line voltage by an angle of 78.5°.

4. The 6-A current in the coil can be resolved into two components. One component is the in-phase current. The second component, or quadrature current, lags the line voltage by 90° because of the inductive reactance in this branch.

6. The vector diagram for the circuit is shown in Figure 8–9. The in-phase current for the coil (1.2 A) is placed on the line voltage vector. The quadrature component of the current (5.88 A) is in a downward direction at an angle of 90° to the line voltage. The vector sum of these components is the current taken by the coil (6 A). The phase angle between the coil current and the line voltage is 78.5°. The current taken by the resistance branch (4 A) is added to the in-phase current of the coil circuit. Thus, the total in-phase current is 5.2 A. The circuit must be supplied with 5.2 A in phase with the line voltage and a quadrature current of 5.88 A lagging the line voltage by 90°. The vector sum of these two components is the line current (7.85 A). The line current lags the line voltage by 48.5°. The total line current is the hypotenuse of a right triangle in the vector diagram of Figure 8–9:

PARALLEL CIRCUIT WITH BRANCHES CONTAINING R AND X_C

Another type of parallel circuit is shown in Figure 8–6. In this circuit, two branches contain noninductive resistance loads and a third branch contains a capacitor. Assuming that the capacitor has negligible resistance, the current in the capacitive branch leads the line voltage by 90 electrical degrees. This means that the line current is the vector sum of the currents in the branches.

PROBLEM 3

Statement of the Problem

The circuit shown in Figure 8–6 contains noninductive resistance and capacitance. For this circuit:

1. Find the current taken by each branch.

2. Construct a vector diagram.

3. Find the total or line current.

4. Find the power taken by the parallel circuit.

5. Find the power factor for the parallel circuit.

6. Find the phase angle.

7. Find the combined impedance.

Solution

1. Branches 1 and 2 contain pure resistance only. The current in each of these branches is in phase with the line voltage.

The total in-phase current for the parallel circuit is the sum of the currents in the first two branches: 8 + 4 = 12 A. The quadrature (out-of-phase) component of current is supplied to the capacitor load in branch 3. This current leads the line voltage by 90° and is given by

2. The vector diagram for the circuit is given in Figure 8–7. The two in-phase current values are placed on the line voltage vector. The total in-phase current is 12 A. The current in the capacitive branch is drawn on the vector diagram in a vertical direction from point 0. Thus, the quadrature current leads the line voltage by 90°. The line current is the vector sum of the total in-phase current and the leading quadrature cur- rent. Note that the line current leads the line voltage by the angle fJ. As a result, this parallel circuit operates with a leading power factor.

3. The line current is the hypotenuse of the right triangle shown in Figure 8–7:

6. The line current leads the line voltage by a phase angle (fJ) of 22.6°.

7. The combined impedance (in ohms) of the parallel circuit is

Another formula that can be used to determine the impedance in a circuit that contains both resistance and capacitive reactance connected in parallel is

PARALLEL CIRCUIT WITH BRANCHES CONTAINING R AND Z_coil

The parallel circuit shown in Figure 8–8 contains two branches. One branch contains a pure resistance of 30 n. The second branch contains a load that has both resistance and inductance. This load is similar to a motor or transformer. The symbol Z_coil is used instead of X because of the coil resistance. It should be noted, however, that the value of Z_coil applies only to the impedance of the coil and should not be confused with the value for the total impedance of the circuit, which is Z total In this circuit, a wattmeter is used to measure the true power of the circuit, and ammeters are used to measure the total current flow and the current flow through each branch. In this circuit, the current will lag the voltage by some value less than 90°.

PROBLEM 4

Statement of the Problem

For the circuit in Figure 8–8, the following items are to be determined:

1. The current taken by each branch

2. The resistance of the coil

3. The power factor of the coil

4. The in-phase component of current in the coil

5. The quadrature component of current in the coil

6. Total impedance of the circuit

Draw a vector diagram for the circuit, and determine (1) the line current and (2) the circuit power factor.

Solution

1. The current in each branch of the circuit is given by Ohm’s law:

The true power taken by the resistance branch is subtracted from the total power taken by the parallel circuit to find the power taken by the coil. Thus, the actual power used in this coil is coil = 624 – 480 = 144 W Therefore, the resistance of the coil is

3. To find the power factor of the coil, it is assumed that the coil is a series circuit containing resistance and inductive reactance. For this case, the power factor is expressed as follows:

For a power factor of 0.20, the coil current lags behind the line voltage by an angle of 78.5°.

4. The 6-A current in the coil can be resolved into two components. One component is the in-phase current. The second component, or quadrature current, lags the line voltage by 90° because of the inductive reactance in this branch.

6. The vector diagram for the circuit is shown in Figure 8–9. The in-phase current for the coil (1.2 A) is placed on the line voltage vector. The quadrature component of the current (5.88 A) is in a downward direction at an angle of 90° to the line voltage. The vector sum of these components is the current taken by the coil (6 A). The phase angle between the coil current and the line voltage is 78.5°. The current taken by the resistance branch (4 A) is added to the in-phase current of the coil circuit. Thus, the total in-phase current is 5.2 A. The circuit must be supplied with 5.2 A in phase with the line voltage and a quadrature current of 5.88 A lagging the line voltage by 90°. The vector sum of these two components is the line current (7.85 A). The line current lags the line voltage by 48.5°. The total line current is the hypotenuse of a right triangle in the vector diagram of Figure 8–9: