science universe

CLAMP-ON AMMETERS

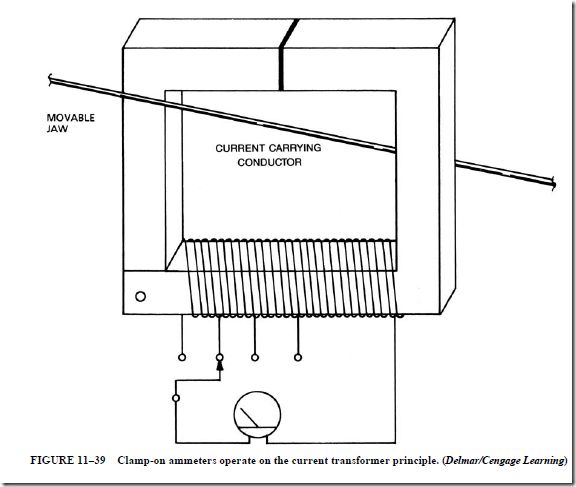
Another meter frequently used is the clamp-on ammeter (Figure 11–38). Most of these meters operate on the current transformer principle. The movable jaw is the core of a cur- rent transformer. The range selection switch connects the meter to different taps on the transformer (Figure 11–39). The conductor around which the movable jaw is connected forms a one-turn primary for the transformer. The secondary is the winding around the iron core. The movable tap changes the turns ratio of the transformer.

If the current is too low to be measured easily, extra turns of wire can be wrapped around the movable jaw. Each turn of wire increases the scale factor of the meter. For example, if two turns of wire are wrapped around the movable jaw, the ammeter reading

will double. To determine the actual amount of current in the circuit, it would be necessary to divide the reading by 2. If 10 turns of wire are wrapped around the movable jaw, the reading would have to be divided by 10.

The advantage of the clamp-on ammeter is that the circuit does not have to be broken to make measurements. This is a great advantage when it is necessary to check the current draw of a piece of operating equipment.

THE OSCILLOSCOPE

Many of the electronic control systems in today’s industry produce voltage pulses that are meaningless to a volt-ohm-milliammeter (VOM). In many instances, it is necessary to know not only the amount of voltage present at a particular point but also the length or duration of the pulse and its frequency. Some pulses may be less than one volt and last for only

a millisecond. A VOM would be useless for measuring many of these things. It is therefore necessary to use an oscilloscope to learn what is actually happening in the circuit.

The oscilloscope is a powerful tool and will perform many jobs that will not be dis- cussed in this text. The first thing to understand about an oscilloscope is that it is a volt- meter. It does not measure current, resistance, or watts. The oscilloscope not only measures the voltage, it draws a picture of it. What the oscilloscope actually does is measure a volt- age during a particular period of time, creating a two-dimensional image.

Voltage Range Selection

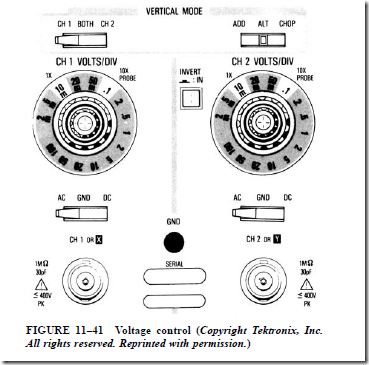
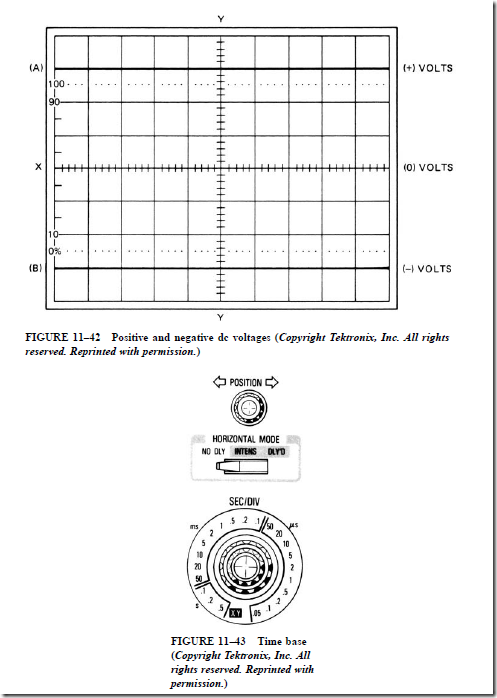
The oscilloscope is divided into two main sections. One section is the voltage section, and the other is the time base. The display of the oscilloscope is divided by vertical and horizontal lines (Figure 11–40). Voltage is measured on the vertical, or Y, axis of the display, and time is measured on the X axis. When using a VOM, a range selection switch is used to determine the full-scale value of the meter. Ranges of 600, 300, 60, and 12 V are common. Having the ability to change ranges permits more accurate measurements to be made. In addition, the oscilloscope has a voltage range selection switch (Figure 11–41). The voltage range-selection switch on an oscilloscope selects volts per division instead of volts full scale. The voltage range switch shown in Figure 11–41 is set for 10 m at the IX position. This means that each of the lines in the vertical direction or on the Y axis of the display has a value of 10 mV. Assume that the oscilloscope has been adjusted to permit 0 V to be.

shown on the centerline of the display. If the oscilloscope probe is connected to a positive voltage of 30 mV, the trace would rise to the position shown in Figure 11–42A. If the probe is connected to a negative 30 mV, the trace will fall to the position shown in Figure 11–42B. Note that the oscilloscope has the ability to display both positive and negative voltages. If the range switch is changed to 20 V per division, Figure 11–42A would be displaying 60 V positive.

The Time Base

The next section of the oscilloscope to become familiar with is the time base (Figure 11–43). The time base is calibrated in seconds per division and has range values from seconds to microseconds. The time base controls the value of the division of the lines in the horizontal direction. If the time base is set for 5 ms per division, the trace will sweep from one division to the division beside it in 5 ms. With the time base set in this position, it will take 50 ms to sweep from one side of the display screen to the other. If the time base is set for 2 µs per division, the trace will sweep the screen in 20 µs.

Measuring Frequency

Because the oscilloscope has the ability to measure the voltage with respect to time, it is possible to compute the frequency of the waveform. The frequency of an ac waveform can be found by dividing the time it takes to complete one cycle into one (1/f ). For example,

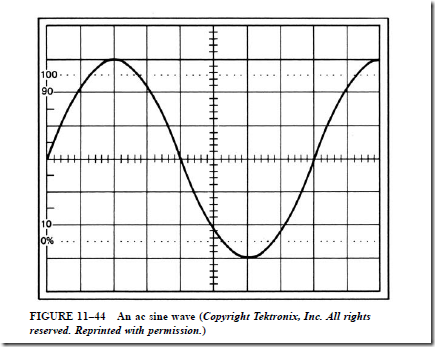
assume that the time base is set for 0.5 ms per division and the voltage range is set for 20 V per division. If the oscilloscope has been set so that the centerline of the display is 0 V, the ac waveform shown in Figure 11–44 has a peak value of 60 V. The oscilloscope displays the peak or peak-to-peak value of voltage and not the RMS or effective value. To measure the frequency, count the time it takes to complete one full cycle. The waveform shown in Figure 11–44 takes 4 ms to complete one full cycle. The frequency is, therefore, 250 Hz (1/0.004 = 250).

Attenuated Probes

Most oscilloscopes use a probe that acts as an attenuator. An attenuator is a device that divides or makes smaller the input signal (Figure 11–45). An attenuated probe is used to permit higher voltage readings than are normally possible. For example, most attenuated probes are 10 to 1. This means if the voltage range switch is set for 5 V per division, the display would actually indicate 50 V per division. If the voltage range switch is set for 2 V per division, each division on the display actually has a value of 20 V per division.

Probe attenuators are made in different styles by different manufacturers. In some probes the attenuator is located in the probe head itself, whereas in others the attenuator is located at the scope input. Regardless of the type of attenuated probe used, it may have to be compensated or adjusted. In fact, probe compensation should be checked frequently. Different manufacturers use different methods for compensating their probes, so it is generally necessary to follow the procedures given in the operator’s manual for the oscilloscope being used..

Oscilloscope Controls

The following is a list of common controls found on the oscilloscope. Refer to the oscilloscope shown in Figure 11–46.

1. Power. The power switch is used to turn the oscilloscope on or off.

2. Beam find. This control is used to locate the position of the trace if it is off the display. The beam finder button will indicate the approximate location of the trace. The position controls are then used to move the trace back on the display.

3. Probe adjust. This is a reference voltage point used to compensate the probe. Most probe adjust points produce a square-wave signal of about 0.5 V.

4. Intensity and focus. The intensity control adjusts the brightness of the trace.

A bright spot should never be left on the display because it will burn a spot on the face of the cathode-ray tube (CRT). This burned spot results in permanent damage to the CRT. The focus control sharpens the image of the trace.

5. Vertical position. This control is used to adjust the trace up or down on the display.

If a dual-trace oscilloscope is being used, there will be two vertical position controls. (A dual-trace oscilloscope contains two separate traces, which can be used separately or together.)

6. Ch 1–both–Ch 2. This control determines which channel of a dual-trace oscillo- scope is to be used, or whether they are to both be used at the same time.

7. Add–Alt–Chop. This control is active only when both traces are being displayed at the same time. The add adds the two waves together. Alt stands for alternate. This alternates the sweep between channel 1 and channel 2. The chop mode alternates several times during one sweep. This makes the display appear more stable. The chop mode is generally used when displaying two traces at the same time.

8. AC–Grd–DC. The ac is used to block any dc voltage when only the ac portion of the voltage is to be seen. For instance, assume an ac voltage of a few millivolts to be riding on a dc voltage of several hundred volts. If the voltage range is set high enough so that 100 V dc can be seen on the display, the ac voltage could not be seen. The ac section of this switch inserts a capacitor in series with the probe. The capacitor blocks the dc voltage and permits the ac voltage to pass. Because the 100 V dc has been blocked, the voltage range can be adjusted for millivolts per division, which will permit the ac signal to be seen.

The Grd section of the switch stands for ground. This section grounds the input so the sweep can be adjusted for 0 V at any position on the display. The ground switch grounds at the scope and does not ground the probe. This permits the ground switch to be used when the probe is connected to a live circuit. The dc section permits the oscilloscope to display all of the voltage, both ac and dc, connected to the probe.

9. Horizontal position. This control adjusts the position of the trace from left to right.

10. Auto–normal. This control determines whether the time base will be triggered auto- matically or whether it is to be operated in a free-running mode. If this control is oper- ated in the normal setting, the trigger signal is taken from the line to which the probe is connected. The scope is generally operated with the trigger set in the automatic position.

11. Level. The level control determines the amplitude the signal must reach before the scope triggers.

12. Slope. The slope permits selection as to whether the trace is triggered by a negative or positive waveform.

13. Int–Line–Ext. The Int stands for internal. The scope is generally operated in this mode. In this setting, the trigger signal is provided by the scope. In the line mode, the trigger signal is provided from a sample of the line. The Ext, or external, mode permits the trigger pulse to be applied from an external source.

These are not all the controls shown on the oscilloscope in Figure 11–46, but they are the major controls. Most oscilloscopes contain these controls.

Interpreting Waveforms

Being able to interpret the waveforms on the display of the oscilloscope takes time and practice. When using the oscilloscope, it must be kept in mind that the display shows the voltage with respect to time.

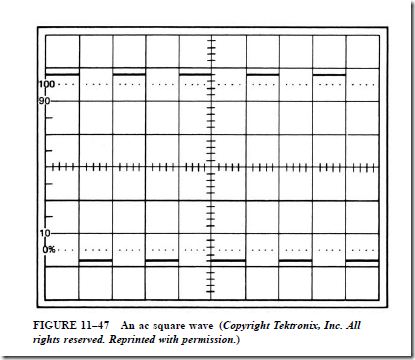
In Figure 11–47, it is assumed that the voltage range has been set for 0.5 V per division, and the time base is set for 2 ms per division. It is also assumed that 0 V has been set

on the centerline of the display. The waveform shown is a square wave. The display shows the voltage rises in the positive direction to a value of 1.4 V and remains there for 2 ms. The voltage then drops to 1.4 V negative and remains there for 2 ms before going back to positive. Because the voltage changes between positive and negative, it is an ac voltage. The length of one cycle is 4 ms. The frequency is, therefore, 250 Hz (1/0.004 = 250).

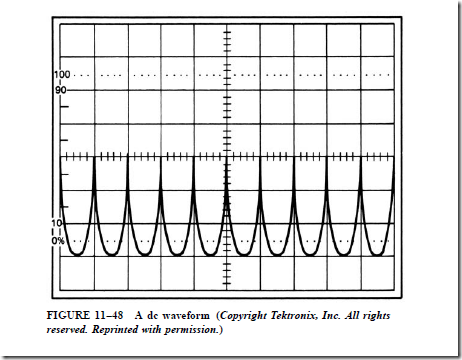
In Figure 11–48, the oscilloscope has been set for 50 mV per division and 20 µs per division. The display shows a voltage that is negative to the probe’s ground lead and has a peak value of 150 mV. The waveform lasts for 20 µs, which produces a frequency of 50 kHz (1/0.000020 = 50,000). The voltage is dc because it never crosses the zero reference and goes in the positive direction.

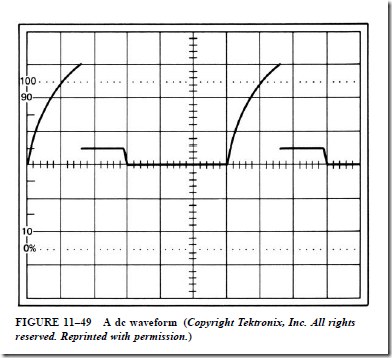
In Figure 11–49, assume that the scope is set for 50 V per division and 0.1 ms per division. The waveform shown rises to a value of 150 V in the positive direction and then drops to about 25 V. The voltage remains at 25 V for 0.15 ms and drops back to 0 V. The voltage remains at 0 for 0.3 ms before the cycle starts over again. The voltage shown is dc because it remains in the positive direction. To compute the frequency, measure from the beginning of one wave to the beginning of the next wave. This is the period of one complete cycle. In this case the length of one cycle is 0.6 ms. The frequency is, therefore, 1666 Hz (1/0.0006 = 1666).

Learning to interpret the waveforms seen on the display of an oscilloscope will take time and practice, but it is well worth the effort. The oscilloscope is the only means by which many of the waveforms and voltages found in electronic circuits can be understood.

SUMMARY

• Instruments used to make ac measurements must have three basic components:

1. A spring mechanism to produce an opposing torque

2. A restoring spring mechanism to restore the pointer to a zero reading

3. A damping system to prevent excessive swinging of the pointer

• The selection of an instrument for a particular use is usually based on its ability to

1. indicate RMS or average values, as required.

2. respond within a certain range of volts or amperes.

3. provide linear calibration in the useful range of the scale.

4. indicate values with the desired accuracy.

5. make measurements at a reasonable cost.

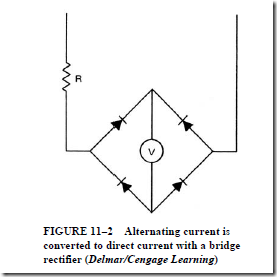
• DC d’Arsonval movement with a rectifier:

1. can be used for ac measurements.

2. develops a torque proportional to the average value of the current in the moving field; the rectifier makes use of the RMS voltage (1.11 times the average voltage value of a sine wave).

3. is accurate only when pure sine-wave quantities are involved.

4. is used in most multimeters.

a. A multimeter used as a voltmeter has a high-resistance linear scale and uses relatively little power.

b. A multimeter used as an ammeter measures in microamperes or milliamperes.

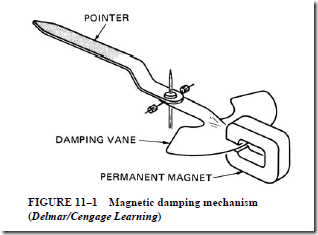
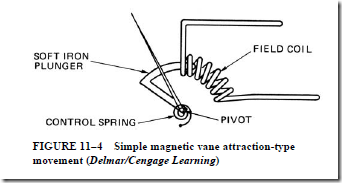
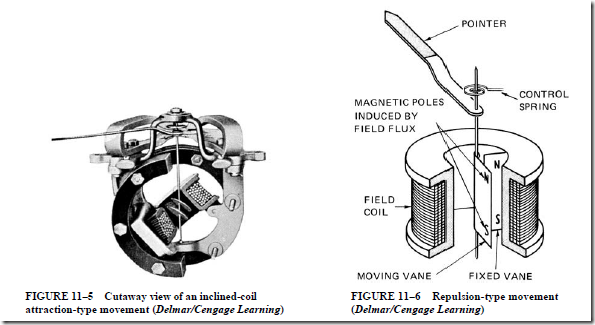
• Magnetic vane attraction movement has a soft iron plunger that projects into a stationary field coil. Also:

1. Current in the field coil produces a magnetic force that pulls the plunger deeper into the coil.

2. The instantaneous value of this force is proportional to the square of the RMS current value in the coil.

3. The torque developed in turning the movement is independent of current direction; thus, the instrument can be used for ac or dc measurements.

4. The scale numbers are crowded at the lower end and expanded for the high end of the scale.

5. This instrument is commonly used in low-cost ammeters.

6. This instrument can be used to make voltage measurements by adding a coil of many turns and a series resistor.

• Inclined coil movement is used in portable and switchboard ammeters and voltmeters.

In addition

1. The scale is long and reasonably linear.

2. An iron vane is free to move in a magnetic field.

3. The vane tends to take a position parallel to the flux.

4. Increasing the current in the field coil increases the force aligning the vanes with the coil flux; thus, the shaft turns and moves the attached pointer across the scale.

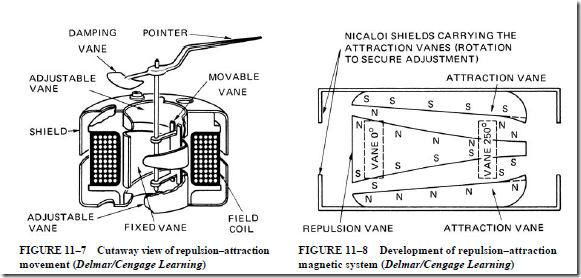
• Repulsion movement employs two soft iron vanes; one vane is attached to the instrument shaft and the other is mounted on the stationary field coil. Also:

1. A repulsion force is developed between the two soft iron vanes because both are affected by the same magnetic field.

2. With no current through the field coil, a control spring holds the movable vane close to the fixed vane.

3. As current increases through the field coil, the like poles of the vanes repel each other and create a torque that turns the shaft.

4. The movement has a reasonably uniform scale and can be used for both current and voltage measurements.

• Repulsion–attraction movement produces a greater torque than do most other movements. The following features also apply:

1. The movable vane is attached to the pointer and is repelled from the wide end of the middle fixed vane as the current through the field coils is increased.

2. The repelling force decreases as the movable vane moves to the narrow end of the middle fixed vane; an attraction force increases as the moving vane comes closer to the upper and lower fixed attraction vanes.

3. A scale length representing 250° of angular deflection can be provided.

4. The distribution of values (volts or amperes) along the scale is determined by the shape and separation of the vanes.

5. Meters can be designed to broaden the scale at any point.

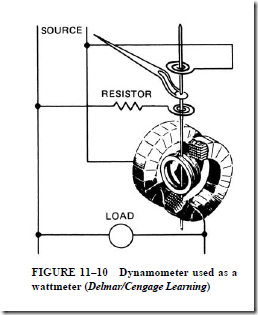
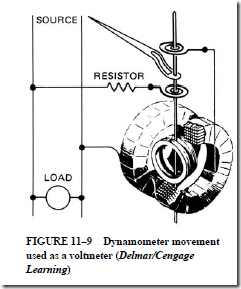
• Dynamometer movement produces a torque by the interaction of magnetic fields; this torque varies with the amount of current in the stationary coils. Both the fixed and moving coils are connected in series. Dynamometer movement

1. can be adapted easily to make voltage measurements by adding the proper series resistor.

2. is more efficient and accurate than d’Arsonval movement.

3. is seldom used as an ammeter for the following reasons:

a. The lead-in spirals to the moving coil can carry only a limited current.

b. Frequency variations introduce error.

c. The resistance of the two coils in series may produce an undesirably high voltage drop across the shunt.

4. is used for instruments measuring power, power factor, and frequency, and to indicate synchronism in ac circuits.

• Practical ranges for moving iron instruments:

1. When the instrument is used for ammeters, its physical size is influenced by the amount of heat to be dissipated and the size of the connection terminals to be supported.

a. For small panel instruments, 100 A is the maximum practical current rating.

b. For large portable instruments, 200 A is the maximum rating.

c. Some large ammeters for switchboard use are rated as high as 600 A.

d. Shunts are not satisfactory for moving iron instruments.

e. It is standard practice to use an instrument current transformer to increase the current range.

2. When used as ac voltmeters

a. series resistors are used to extend the scale range for voltages up to 750 V.

b. instrument potential transformers are used with the movement for voltages greater than 750 V; in many cases, the instrument scale is calibrated to indi- cate the primary voltage directly.

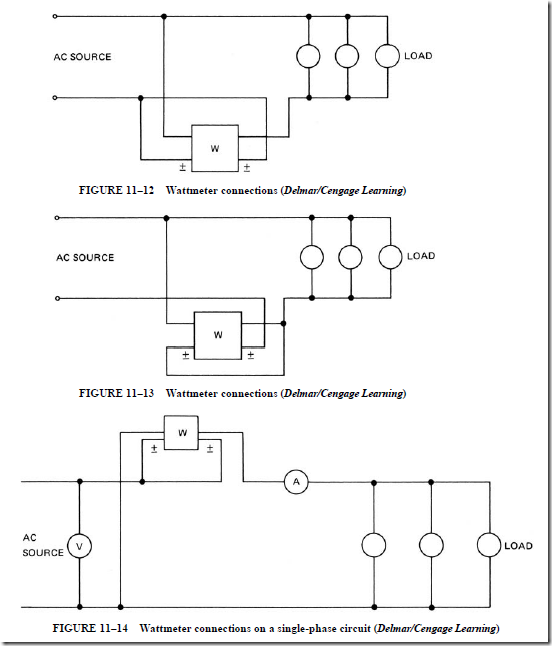
3. When used as a wattmeter

a. the stationary field coils are connected in series with the line so that the flux depends on the current.

b. the moving coils are connected across the line so that the moving coil flux is proportional to the system voltage.

c. the instantaneous torque is proportional to the instantaneous moving coil voltage.

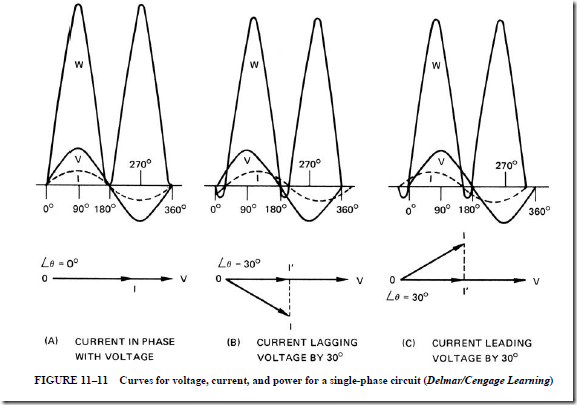
d. pointer deflection is proportional to the power:

Watts = VI cos 8

e. the power curve at any instant is positive.

Also, when using an instrument with a dynamometer movement, the technician must consider the instantaneous direction in each of the coils. There are two dif- ferent methods of connecting the potential coils of a wattmeter.

a. The potential coil is not connected directly across the load:

True power = wattmeter reading – I2 R of current coil

b. The potential coil is connected across the load voltage:

For this second method, the percentage of error is slightly less as compared to the first method.

A wattmeter is always rated according to its potential and current coil ratings rather than in watts.

4. When used as a varmeter,

a. it indicates the product of the circuit voltage and the current component 90° out of phase with the voltage; that is, it measures the reactive volt- amperes.

b. the varmeter reads VI cos (8 – 90) or VI sin 8; the wattmeter reads VI cos 8.

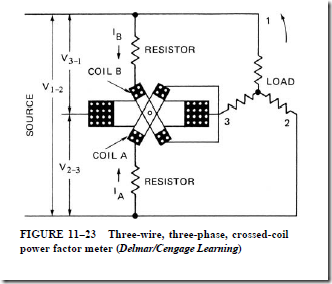
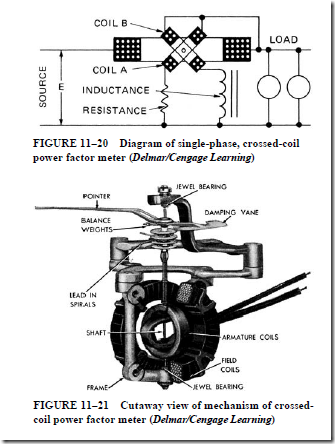
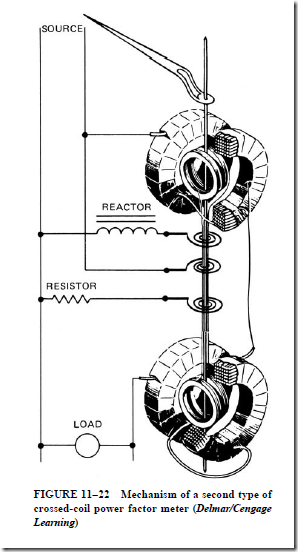
5. When used as a power factor meter,

a. a single-phase power factor meter resembles a single-phase wattmeter.

b. the stationary field coils are connected in series with one side of the line.

c. the field coils carry the line current and produce the field flux.

d. it differs from the wattmeter in that it has no control springs.

e. the flux of the moving coils reacts with that of the field coil to produce a torque proportional to the in-phase component of current.

f. the torque magnitude is determined by the amount of quadrature current.

g. the resultant of the torque due to the in-phase component of current and that due to the quadrature component determines the pointer position and shows the lagging or leading power factor value.

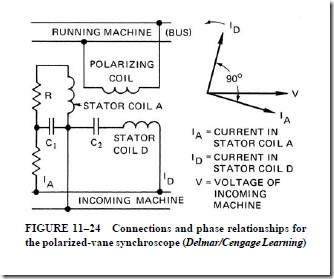
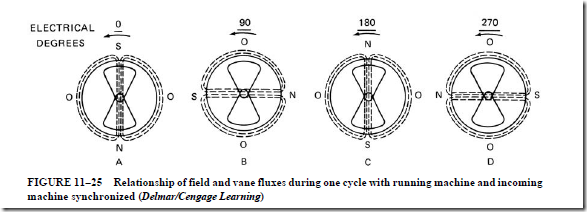
• Synchroscope

1. The synchroscope shows the relative phase angle and the frequency difference between two alternating voltages to indicate when two alternators are in phase.

2. This instrument also indicates whether the frequency of the incoming generator is higher or lower than that of the generator already connected to the line.

3. Both the polarized-vane type and the moving-iron type of synchroscope are commonly used.

4. These instruments are designed for operation on single-phase circuits. They may be used with three-phase generators if the phase sequences of the generators are known.

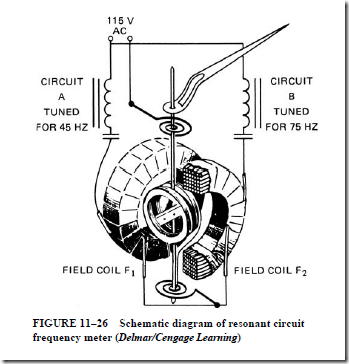
• A commonly used frequency meter is known as the resonant circuit meter.

1. The structure of this meter resembles that of the dynamometer.

2. The two field coils are alike and are connected so that their fluxes oppose each other.

3. Each field coil is connected in series with an inductor–capacitor combination.

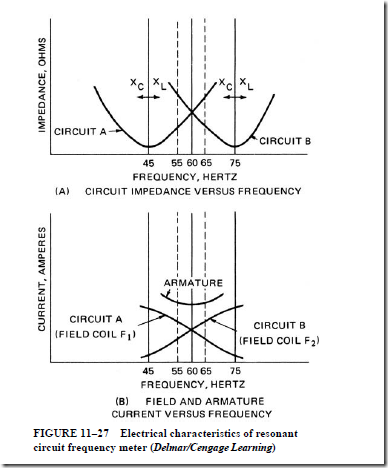
Because of the constants of this combination,

a. series resonance occurs below the normal operating frequency in one field coil and above the normal frequency in the other field coil.

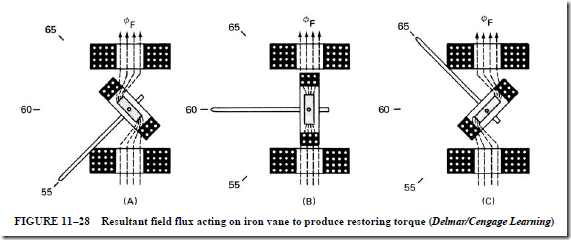
b. the current in the armature is the vector sum of the currents in the two field coils. The value of lead or lag depends on which field current is greater.

c. when the frequency is such that the leading and lagging currents are equal, the armature current is in phase with the terminal voltage.

d. the pointer movement is caused by the torque, due to the resultant flux acting on the iron vane; this torque is proportional to the product of the armature flux and the in-phase component of the resultant field flux.

• Recording instruments

1. provide a graphical record of the actual circuit conditions at any time.

2. are grouped into two broad categories:

a. Instruments that record electrical values such as volts, amperes, watts, power factor, and frequency

b. Instruments that record nonelectrical quantities such as temperature

3. use a permanent-magnet, moving-coil-type construction for dc circuits.

4. for ac circuits, may use either the moving-iron or the dynamometer-type construction.

A strip-chart recorder is the most commonly used graphical recording instrument:

1. A strip of paper 4 to 6 in. wide and up to 60 ft long is used for the permanent record.

2. The long chart means that the record can cover a considerable amount of time.

3. The chart can be operated at a relatively high speed to provide a detailed graphical record.

Some recording instruments have a spring-type clock mechanism wound by a small electric motor. This mechanism guarantees that a power failure will not stop the chart

motion until the spring runs down. Some of the larger instruments require a large amount of power for operation. The amount of power required can be reduced by using electronic amplifiers.

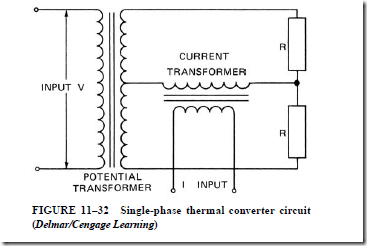
• The thermal converter

1. changes ac voltage and current signals into a dc signal in millivolts; this signal is proportional to the product of VI cos 8.

2. can be used to measure ac watts using a dc recording or indicating device.

The thermocouple output (dc millivolt signal) is proportional to ac power in the circuit to which the V and I inputs are attached.

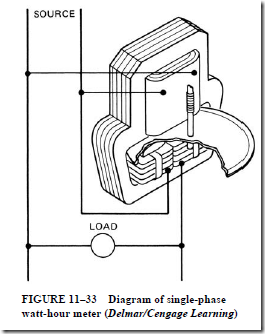
• Watt-hour meter

1. The watt-hour meter determines and adds together (integrates) all of the instantaneous power values to give an indication of the total energy used over a period of time.

2. The watt-hour constant of the meter is the number of watt-hours represented by one revolution of the disc.

3. Each division on the right-hand dial = one kilowatt-hour (kWh).

4. Second dial from the right = 10 kWh.

5. The third dial from the right = 100 kWh.

6. The dial on the left = 1000 kWh.

7. The register ratio is the number of revolutions made by the first gear wheel for one revolution of the right-hand dial pointer.

8. The gear ratio is the number of revolutions made by the meter disc to cause one revolution of the right-hand dial pointer.

9. A full-load adjustment of a meter means that the proper amount of magnetic braking is provided to give the correct speed at the rated voltage and current for a unity power factor.

10. A light-load adjustment is made by moving a shading pole loop to produce a lag in the time phase of part of the potential flux; this adjustment overcomes errors due to friction and torque at light loads.

11. Holes are drilled in the disc 180° apart to overcome the slow rotation (creeping) of the disc at light loads. The disc rotates until one of the hole positions open circuits the eddy currents in the disc. The resulting distortion of the eddy currents produces a locking torque to stop the rotation of the disc.

• Digital multimeter

1. displays reading with individual digits instead of a pointer and scale.

2. has a high input impedance.

3. input impedance remains constant on all voltage ranges.

• The clamp-on ammeter:

1. Most clamp-on ammeters operate on the principle of a current transformer.

2. The range selection switch changes the ratio of the current transformer.

3. The circuit does not have to be broken to measure the current flow.

• The oscilloscope

1. measures voltage and time.

2. can be used to measure frequency.

3. displays a two-dimensional image of the voltage waveform.

4. may use an attenuated probe to permit the measurement of higher voltages.

Achievement Review

1. a. Describe the construction of a magnetic vane, attraction-type instrument movement.

b. Describe the operation of the magnetic vane, attraction-type instrument movement when used as

1. an ac ammeter.

2. an ac voltmeter.

2. Give one advantage and two disadvantages of the magnetic vane, attraction-type instrument movement.

3. Describe the operation of the inclined coil movement, when used as a voltmeter.

4. Explain the operation of a repulsion–attraction instrument movement.

5. A repulsion–attraction instrument movement has a full-scale deflection of 6 mA. The effective resistance of the coil is 3800 D. To use this instrument as a voltmeter with a full-scale deflection of 750 D, a series resistor is added. This resistor has a resistance of 120,000 D. With full-scale deflection, determine the power loss, in watts, in the

a. instrument coil.

b. series resistor.

c. entire instrument.

6. Show the connections for a dc moving coil, permanent-magnet-type movement.

Be sure to show the full-wave rectifier and series resistor used to measure the ac voltage.

7. a. If the losses in the rectifier shown in question 6 are negligible, what reading will the dc voltmeter indicate if the maximum value of the ac voltage measured is 340 V?

b. What factor is used to recalibrate the dc instrument scale to read the effective value of ac volts?

8. a. What are the advantages of using rectifier instruments?

b. What is one limitation of using a rectifier instrument to measure current?

9. Describe the operation of a dynamometer-type movement when used as an ac voltmeter.

10. List several reasons why the dynamometer-type movement is seldom used in ac ammeters.

11. Describe the construction and operation of the dynamometer-type wattmeter.

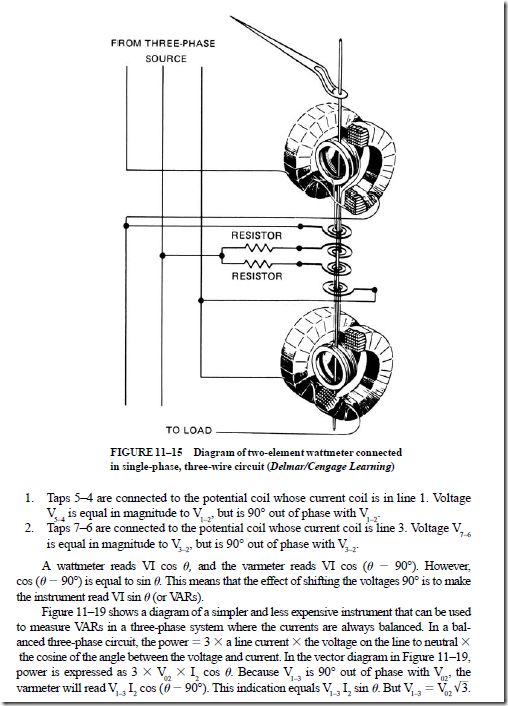
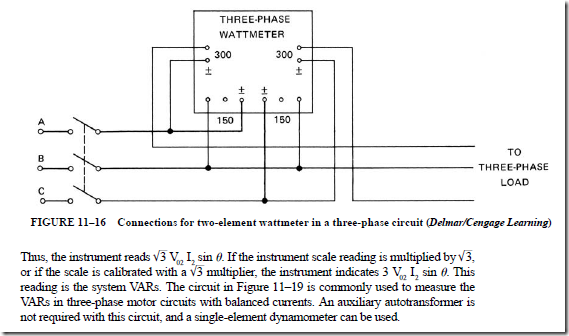
12. Why is it often more satisfactory to use a two-element wattmeter to measure power in a three-phase, three-wire system than it is to use two single-phase wattmeters?

13. a. The current coil (or the potential coil) of a wattmeter can burn out even though the instrument reading is well below the full-scale deflection. Explain why this can happen.

b. What precautions are taken when determining whether the current coil or voltage circuits are overloaded?

14. a. Show the connections for a two-element wattmeter used to measure power in a three-phase, three-wire system.

b. Describe the operation of a two-element wattmeter used to measure three- phase power.

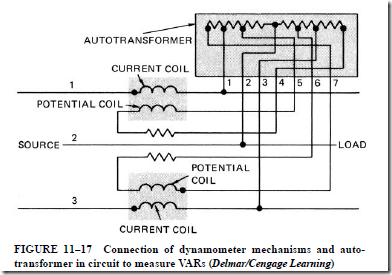
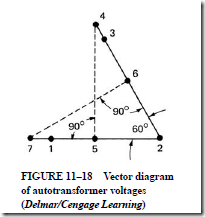
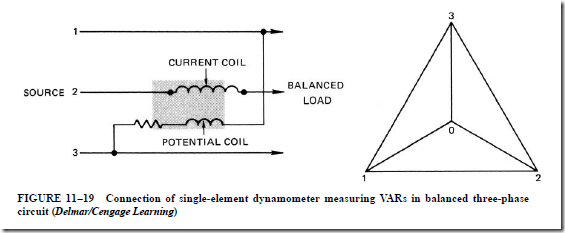
15. How can a dynamometer instrument be used to measure the reactive power in VARs?

16. Describe the operation of

a. a single-phase power factor meter of the crossed-coil type.

b. a three-phase power factor meter of the crossed-coil type.

17. Explain the operation of a polarized-vane synchroscope.

18. Explain the operation of a resonant-type frequency meter.

19. What is the value of a recording instrument? Explain.

20. a. List the parts of a typical single-phase watt-hour meter.

b. Explain the meaning of each of these terms:

1. Register ratio

2. Gear ratio

3. Watt-hour meter disc constant

21. An analog multimeter has a scale factor of 5000 D/V. If the meter is set on the 300-V range, how much current will flow through the meter if it is connected to 240 V?

22. What is a common input impedance for a digital multimeter?

23. What is the principle of operation of most clamp-on ammeters?

24. A clamp-on ammeter has five turns of wire wrapped around its movable jaw. If the meter is indicating a current of 15 A, how much current is actually flowing in the circuit?

25. An oscilloscope indicates an ac waveform. If one cycle is completed in 4 µs, what is the frequency of the waveform?

THERMAL CONVERTERS

Thermal converters change ac voltage and current signals into a dc signal in millivolts. This signal is proportional to the product of VI cos 8. AC watts can be measured using a thermal converter with a dc recording or indicating device.

Figure 11–32 is a schematic diagram of a single-phase thermal converter. The currents in the resistors depend on the values of the voltage and current inputs and the phase angle 8 between the inputs. Thermocouples are attached to each resistor. These thermocouples are connected in series so that their thermal electromotive forces (emfs) subtract. The total thermocouple circuit output is proportional to the temperature difference between the two resistors.

This thermocouple output is also proportional to the difference in power dissipation in the resistors. Thus, the output is equal to a constant times VI cos 8. This means that the dc millivolt signal output of the converter indicates the ac power in the circuit to which the V and I inputs are attached.

The outputs of two of these converters can be connected in series. As a result, a dc voltage is developed that is proportional to the sum of two ac power inputs. In summary, three-phase ac power can be measured in two ways: (1) using the two-wattmeter method or (2) using one dc millivoltmeter or recorder.

External phase-shifting autotransformers can be added so that the same circuit will measure three-phase VARs.

THE WATT-HOUR METER

Direct Current Fundamentals explained that electrical work is the use of electrical energy over a period of time. Electric power is the rate at which electrical energy is used. The basic unit of measurement for electric power is the watt. In ac circuits, power in watts is the product of the potential in volts, the current in amperes, and the power factor. The basic unit of measurement for electric energy is the watt-hour. This value is found by multiplying the power (in watts) of a circuit by the total time in hours during which the power is used in the circuit. The watt-hour meter measures the electrical energy consumed in the circuit.

The connections for a typical single-phase watt-hour meter are shown in Figure 11–33. The watt-hour meter is similar to the wattmeter because it also has current coils connected in series with the load and potential coils connected across the line voltage. The interacting magnetic field of the current and voltage coils produces a torque in an armature. This torque is always proportional to the power in the circuit. In the watt-hour meter, the armature is a disc that rotates at a speed proportional to the power in the circuit. The rate at which the disc rotates corresponds to the power. The number of revolutions of the disc corresponds to the total energy used.

Components of the Watt-hour Meter

A single-phase watt-hour meter consists of the following parts: an electromagnetic element, the magnetic braking system, the register, the frame, the base (including terminal connections), and the cover.

An induction-type motor is used in a watt-hour meter. The rotor is an aluminum disc mounted on a shaft. This shaft is free to turn in bearings held in the metal frame. A worm gear drives the gear register. Generally, this gear is cut directly into the shaft. In some instances, the rotor may be suspended magnetically. Guide pins are then used to maintain vertical alignment of the shaft. In all cases, the disc is mounted so that a portion of it rotates in the airgap of the stator assembly or electromagnet.

Operation

The electromagnet has two sets of windings assembled on a laminated soft iron core. The potential coil winding has many turns of fine wire and a high impedance. This winding is connected across the source voltage. The current coil winding consists of a few turns of heavy wire. This winding is connected in series with the metered circuit. The core laminations are riveted together to form a rigid mechanical structure. The permanent alignment that results maintains the correct magnetic flux distribution and so ensures a consistent performance.

A torque results from the interaction between the flux (produced by the current in one of the coils) and the eddy currents (induced in the disc by the flux created by the other coil). This torque causes the disc to turn at any given instant. The current coil conducts the load current. Because this coil has only a few turns of large-size wire, its inductance is very small. This means that the current coil flux is nearly in phase with the load current. The current coil

flux produces eddy currents in the disc. These eddy currents lag the current coil flux by 90°. Recall that an induced emf always lags 90° behind the flux producing it.

The potential coil is highly inductive. Therefore, the current and flux of the potential coil lag the source voltage by nearly 90°. If a load has a unity power factor, then the potential coil flux is in phase with the eddy currents produced by the current coil. The potential coil poles are above that part of the disc where the eddy currents flow. These eddy currents react with the potential coil flux to develop a torque that is proportional to the line voltage and the load current.

The poles on which the current coil is wound are located beneath the part of the disc where the eddy currents from the potential coil flux flow. These eddy currents react with the flux of the current coil. This reaction produces an additional torque that is also proportional to the line voltage and the load current.

Assembly. An electromagnet assembly is shown in Figure 11–34 for a single-phase watt- hour meter. For a load with a power factor other than unity, the eddy currents lag or lead the fluxes with which they react. The amount of lag or lead corresponds to the phase difference between the line voltage and the load current. The torque developed in each of the eddy current and flux reactions is reduced by a proportional amount.

It is possible for the disc to turn at an excessive speed. To prevent this, a magnetic braking system is used. This system consists of two permanent magnets mounted so that the disc is located between the poles of the magnets. As the disc rotates, it cuts the flux of the two permanent magnets. Eddy currents are thus induced in the disc. The eddy currents react with the permanent-magnet flux to produce a damping torque. The torque opposes the meter torque, and the disc turns at the desired speed for a given load.

The gear register is located on the disc shaft and consists of a train of gears driven by a worm gear or a pinion gear. The gear register turns several dial pointers to show the number of times the disc has turned. This means that the watt-hour meter determines and adds together

(integrates) all of the instantaneous power values. As a result, there is an indication of the total energy used over a period of time. Compare this action with that of a wattmeter, which indicates only the instantaneous power or rate of energy use in a circuit.

Interpreting the Dial Readings of the Watt-hour Meter

The watt-hour constant of the meter is the number of watt-hours represented by one revolution of the disc. The pointer of the right-hand dial of the gear register indicates one kilowatt-hour after the disc makes the required number of revolutions. The gearing is arranged so that each division on the right-hand dial is one kilowatt-hour (kWh). On the second dial from the right, each division represents 10 kWh. The third dial from the right has divisions representing 100 kWh. For the dial on the left, each division represents 1000 kWh.

The register ratio is the number of revolutions made by the first gear wheel as it meshes with the worm or pinion gear on the disc shaft for one revolution of the right-hand dial pointer. The gear ratio is the number of revolutions made by the meter disc in causing one revolution of the right-hand dial pointer.

DIGITAL MULTIMETERS

Digital multimeters have become increasingly popular. The most apparent difference between digital meters and analog meters is the fact that digital meters display their read- ings in discrete digits rather than with a pointer and scale. A digital multimeter is shown in Figure 11–35. Some digital meters have a range switch similar to the range switch used with analog meters. This switch sets the full range value of the meter. Many digital meters have volt- age range settings from 200 mV to 2000 V. The lower ranges are used for accuracy. For example, assume that it is necessary to measure a voltage of 16 V. The meter will be able to make a more accurate measurement when set on the 20-V range than it will when set on the 2000-V range.

Some digital meters do not contain a range setting control. These meters are known as autoranging meters. They contain a function control, which permits selection of the electrical quantity to be measured such as ac volts, dc volts, or ohms. When the meter probes are connected to the object to be tested, the meter automatically selects the proper range and displays the value. Appearance is not the only difference between digital meters and analog meters. Analog meters change scale value by inserting or removing resistance from the meter circuit (Figure 11–36). The typical resistance of an analog meter is 20,000 D/V for dc and 5000 D/V ac. This means that if the meter is set for a full-scale value of 60 V, there will be 1.2 MD of resistance connected in series with the meter if it is being used to measure dc (60 X 20,000 = 1,200,000) and 300 kD if it is being used to measure ac (60 X 5000 = 300,000). The impedance of the meter is of little concern if it is used to measure circuits that are connected to a high-current source. For example, assume that the voltage of a 480-V panel is to be measured with a multimeter having a resistance of 5000 D/V. If the meter is set on the 600-V range, the resistance connected in series with the meter is 3 MD (600 X 5000 = 3,000,000). This will permit a current of 160 µA to flow in the meter circuit (480/3,000,000 = 0.000160). This 160 µA of current would not be enough to affect the circuit being tested.

Now assume that this meter is to be used to test a 24-V circuit that has a current flow of 100 µA. If the 60-V range is used, the meter circuit contains a resistance of 300 kilohms (60 X 5000 = 300,000). This means that a current of 80 µA will flow when the meter is

connected to the circuit (24/300,000 = 0.000080). The connection of the meter to the circuit has changed the entire circuit operation.

Digital meters do not have this problem. Most digital meters have an input impedance of about 10 MD on all ranges. This is accomplished by using field effect transistors (FETs) and a voltage divider circuit. A simple schematic for this circuit is shown in Figure 11–37. Notice inthis circuit that the meter input is connected across 10 MD of resistance regardless of the range setting of the meter. If this meter is used to measure the voltage of the 24-V circuit, a current of µA will flow through the meter. This is not enough current to upset the rest of the circuit, and voltage measurements can be made accurately.

THERMAL CONVERTERS

Thermal converters change ac voltage and current signals into a dc signal in millivolts. This signal is proportional to the product of VI cos 8. AC watts can be measured using a thermal converter with a dc recording or indicating device.

Figure 11–32 is a schematic diagram of a single-phase thermal converter. The currents in the resistors depend on the values of the voltage and current inputs and the phase angle 8 between the inputs. Thermocouples are attached to each resistor. These thermocouples are connected in series so that their thermal electromotive forces (emfs) subtract. The total thermocouple circuit output is proportional to the temperature difference between the two resistors.

This thermocouple output is also proportional to the difference in power dissipation in the resistors. Thus, the output is equal to a constant times VI cos 8. This means that the dc millivolt signal output of the converter indicates the ac power in the circuit to which the V and I inputs are attached.

The outputs of two of these converters can be connected in series. As a result, a dc voltage is developed that is proportional to the sum of two ac power inputs. In summary, three-phase ac power can be measured in two ways: (1) using the two-wattmeter method or (2) using one dc millivoltmeter or recorder.

External phase-shifting autotransformers can be added so that the same circuit will measure three-phase VARs.

THE WATT-HOUR METER

Direct Current Fundamentals explained that electrical work is the use of electrical energy over a period of time. Electric power is the rate at which electrical energy is used. The basic unit of measurement for electric power is the watt. In ac circuits, power in watts is the product of the potential in volts, the current in amperes, and the power factor. The basic unit of measurement for electric energy is the watt-hour. This value is found by multiplying the power (in watts) of a circuit by the total time in hours during which the power is used in the circuit. The watt-hour meter measures the electrical energy consumed in the circuit.

The connections for a typical single-phase watt-hour meter are shown in Figure 11–33. The watt-hour meter is similar to the wattmeter because it also has current coils connected in series with the load and potential coils connected across the line voltage. The interacting magnetic field of the current and voltage coils produces a torque in an armature. This torque is always proportional to the power in the circuit. In the watt-hour meter, the armature is a disc that rotates at a speed proportional to the power in the circuit. The rate at which the disc rotates corresponds to the power. The number of revolutions of the disc corresponds to the total energy used.

Components of the Watt-hour Meter

A single-phase watt-hour meter consists of the following parts: an electromagnetic element, the magnetic braking system, the register, the frame, the base (including terminal connections), and the cover.

An induction-type motor is used in a watt-hour meter. The rotor is an aluminum disc mounted on a shaft. This shaft is free to turn in bearings held in the metal frame. A worm gear drives the gear register. Generally, this gear is cut directly into the shaft. In some instances, the rotor may be suspended magnetically. Guide pins are then used to maintain vertical alignment of the shaft. In all cases, the disc is mounted so that a portion of it rotates in the airgap of the stator assembly or electromagnet.

Operation

The electromagnet has two sets of windings assembled on a laminated soft iron core. The potential coil winding has many turns of fine wire and a high impedance. This winding is connected across the source voltage. The current coil winding consists of a few turns of heavy wire. This winding is connected in series with the metered circuit. The core laminations are riveted together to form a rigid mechanical structure. The permanent alignment that results maintains the correct magnetic flux distribution and so ensures a consistent performance.

A torque results from the interaction between the flux (produced by the current in one of the coils) and the eddy currents (induced in the disc by the flux created by the other coil). This torque causes the disc to turn at any given instant. The current coil conducts the load current. Because this coil has only a few turns of large-size wire, its inductance is very small. This means that the current coil flux is nearly in phase with the load current. The current coil

flux produces eddy currents in the disc. These eddy currents lag the current coil flux by 90°. Recall that an induced emf always lags 90° behind the flux producing it.

The potential coil is highly inductive. Therefore, the current and flux of the potential coil lag the source voltage by nearly 90°. If a load has a unity power factor, then the potential coil flux is in phase with the eddy currents produced by the current coil. The potential coil poles are above that part of the disc where the eddy currents flow. These eddy currents react with the potential coil flux to develop a torque that is proportional to the line voltage and the load current.

The poles on which the current coil is wound are located beneath the part of the disc where the eddy currents from the potential coil flux flow. These eddy currents react with the flux of the current coil. This reaction produces an additional torque that is also proportional to the line voltage and the load current.

Assembly. An electromagnet assembly is shown in Figure 11–34 for a single-phase watt- hour meter. For a load with a power factor other than unity, the eddy currents lag or lead the fluxes with which they react. The amount of lag or lead corresponds to the phase difference between the line voltage and the load current. The torque developed in each of the eddy current and flux reactions is reduced by a proportional amount.

It is possible for the disc to turn at an excessive speed. To prevent this, a magnetic braking system is used. This system consists of two permanent magnets mounted so that the disc is located between the poles of the magnets. As the disc rotates, it cuts the flux of the two permanent magnets. Eddy currents are thus induced in the disc. The eddy currents react with the permanent-magnet flux to produce a damping torque. The torque opposes the meter torque, and the disc turns at the desired speed for a given load.

The gear register is located on the disc shaft and consists of a train of gears driven by a worm gear or a pinion gear. The gear register turns several dial pointers to show the number of times the disc has turned. This means that the watt-hour meter determines and adds together

(integrates) all of the instantaneous power values. As a result, there is an indication of the total energy used over a period of time. Compare this action with that of a wattmeter, which indicates only the instantaneous power or rate of energy use in a circuit.

Interpreting the Dial Readings of the Watt-hour Meter

The watt-hour constant of the meter is the number of watt-hours represented by one revolution of the disc. The pointer of the right-hand dial of the gear register indicates one kilowatt-hour after the disc makes the required number of revolutions. The gearing is arranged so that each division on the right-hand dial is one kilowatt-hour (kWh). On the second dial from the right, each division represents 10 kWh. The third dial from the right has divisions representing 100 kWh. For the dial on the left, each division represents 1000 kWh.

The register ratio is the number of revolutions made by the first gear wheel as it meshes with the worm or pinion gear on the disc shaft for one revolution of the right-hand dial pointer. The gear ratio is the number of revolutions made by the meter disc in causing one revolution of the right-hand dial pointer.

DIGITAL MULTIMETERS

Digital multimeters have become increasingly popular. The most apparent difference between digital meters and analog meters is the fact that digital meters display their read- ings in discrete digits rather than with a pointer and scale. A digital multimeter is shown in Figure 11–35. Some digital meters have a range switch similar to the range switch used with analog meters. This switch sets the full range value of the meter. Many digital meters have volt- age range settings from 200 mV to 2000 V. The lower ranges are used for accuracy. For example, assume that it is necessary to measure a voltage of 16 V. The meter will be able to make a more accurate measurement when set on the 20-V range than it will when set on the 2000-V range.

Some digital meters do not contain a range setting control. These meters are known as autoranging meters. They contain a function control, which permits selection of the electrical quantity to be measured such as ac volts, dc volts, or ohms. When the meter probes are connected to the object to be tested, the meter automatically selects the proper range and displays the value. Appearance is not the only difference between digital meters and analog meters. Analog meters change scale value by inserting or removing resistance from the meter circuit (Figure 11–36). The typical resistance of an analog meter is 20,000 D/V for dc and 5000 D/V ac. This means that if the meter is set for a full-scale value of 60 V, there will be 1.2 MD of resistance connected in series with the meter if it is being used to measure dc (60 X 20,000 = 1,200,000) and 300 kD if it is being used to measure ac (60 X 5000 = 300,000). The impedance of the meter is of little concern if it is used to measure circuits that are connected to a high-current source. For example, assume that the voltage of a 480-V panel is to be measured with a multimeter having a resistance of 5000 D/V. If the meter is set on the 600-V range, the resistance connected in series with the meter is 3 MD (600 X 5000 = 3,000,000). This will permit a current of 160 µA to flow in the meter circuit (480/3,000,000 = 0.000160). This 160 µA of current would not be enough to affect the circuit being tested.

Now assume that this meter is to be used to test a 24-V circuit that has a current flow of 100 µA. If the 60-V range is used, the meter circuit contains a resistance of 300 kilohms (60 X 5000 = 300,000). This means that a current of 80 µA will flow when the meter is

connected to the circuit (24/300,000 = 0.000080). The connection of the meter to the circuit has changed the entire circuit operation.

Digital meters do not have this problem. Most digital meters have an input impedance of about 10 MD on all ranges. This is accomplished by using field effect transistors (FETs) and a voltage divider circuit. A simple schematic for this circuit is shown in Figure 11–37. Notice inthis circuit that the meter input is connected across 10 MD of resistance regardless of the range setting of the meter. If this meter is used to measure the voltage of the 24-V circuit, a current of µA will flow through the meter. This is not enough current to upset the rest of the circuit, and voltage measurements can be made accurately.

SYNCHROSCOPES

The synchroscope is an instrument that shows the relative phase angle and the frequency difference between two alternating voltages. This instrument indicates when alternators are in phase. It also indicates whether the frequency of the incoming generator is higher or lower than that of the generator already connected to the line.

There are a number of versions of synchroscopes available. Two commonly used synchroscopes are the polarized-vane type and the moving iron type. These synchroscopes are

designed for operation on single-phase circuits. Both devices show when the voltages of two single-phase ac generators are synchronized. They also can be used with three-phase genera- tors if the phase sequences of the generators are known.

Polarized-Vane Synchroscope

The polarized-vane synchroscope (Figure 11–24) uses a mechanism that is similar in physical structure to that of the polarized-vane power factor meter. The basic difference in this mechanism is that the polarizing coil is wound as a potential coil rather than as a current coil. The stator winding has a phase-splitting network and is connected across one phase of the incoming generator. The polarizing winding for the vanes is connected across the corresponding phase of the generator already on the line.

The stator winding of a polarized-vane synchroscope is arranged so that a two- phase field effect is obtained by a phase-splitting network, as shown in Figure 11–24.

In the stator network system, capacitor C causes current I to lead the voltage (V) by a large phase angle of 75° to 80°. Current I lags V because of the inductance of coil A. The amount of lag is about 10° to 15°. As a result, the angle between currents I is 90°.

Operation of the Polarized-Vane Synchroscope

Figure 11–25 shows the relationships between the field and vane fluxes for one cycle with the voltages of the two generators in synchronism. If the rotating field is 61 Hz and the field of the vane polarization is 60 Hz, then the rotating field is 1⁄60 th revolution ahead each time the vanes reach maximum magnetism in one polarity. The vanes line up with the position of the field at the instant of maximum vane magnetism. Thus, each complete cycle of vane polarization brings the vanes 1⁄60 th of a turn further around. For this case, the vanes make one complete revolution in one second. If the stator field rotates at 62 Hz, the vanes will rotate twice as fast. That is, they will make two revolutions in one second.

Assume that a frequency of 59 Hz is applied to the stator windings and 60 Hz is applied in the polarizing coil. The vanes will then make one revolution per second in the opposite direction. In other words, the speed of the pointer is the difference in frequency of the incoming generator and the machine already connected to the line wires. The direction of rotation of the pointer shows whether the speed of the incoming generator is too fast or too slow. When the two generators are operating at the same frequency, the vanes do not rotate. The position of the pointer for this case indicates the phase relationship between the two voltages.

FREQUENCY METERS

Electric motors, transformers, and other types of machines require the correct volt- age for efficient operation. These machines are also designed to operate at a definite frequency. In the case of electric clocks, it is very important that the frequency be accurately indicated. A variation of a small fraction of a cycle, continued through a long period of time, can result in serious errors in time indication on an electric clock. Therefore, electric power systems must operate at the correct frequency. It is obvious that frequency- indicating instruments must be used to show the frequency of a system.

Standard practice requires that ac systems operate at a single frequency. Thus, frequency indications are required to cover only a narrow band of frequency values on either side of the normal frequency. This means that the accuracy of the instrument is improved over what it would be if the instrument covered a wide frequency range.

Resonant Circuit Frequency Meter

One type of commonly used frequency meter is the resonant circuit meter. The physical structure of such a frequency meter resembles that of the dynamometer.

A schematic diagram of a resonant circuit frequency meter is shown in Figure 11–26. The use of two series resonant circuits provides a deflecting torque that has a definite relationship to the applied voltage regardless of its magnitude. The two field coils are alike and are connected so that their fluxes oppose each other. Each field coil is

connected in series with an inductor–capacitor combination. The constants of this combination permit series resonance below the normal operating frequency in one field coil and series resonance above the normal frequency in the other field coil. If a frequency meter is designed to operate on a normal frequency at 60 Hz, the field circuits are designed so that they are in resonance at 45 Hz and 75 Hz. The armature coil is connected through lead-in spirals. It has almost no countertorque effects and carries the total current of both field circuits.

Changing Circuit Impedance. The change in the circuit impedance of each field coil circuit with a change in frequency is shown in Figure 11–27. Figure 11–27B shows the currents in each of the field circuits and the total armature current. The magnitudes of these currents vary with frequency. Within the operating range of the frequency, the curves show that the impedance of the circuit resonating at 45 Hz is inductive. For the circuit resonating at 75 Hz, the impedance is capacitive. This means that the current in field coil F in circuit A always lags the terminal voltage. Also, the current in field coil F in circuit B always leads the voltage. The actual value of lag or lead and the magnitude of the current in each circuit all depend on the frequency. The current in the armature is the vector sum of the two field currents. Both the armature current and the armature flux lead or lag the terminal voltage, depending on which field current is greater. When the frequency is such that the leading and lagging currents are equal, the armature current is in phase with the terminal voltage.

Field Flux

The fluxes of the field coils oppose each other. Thus, the resultant field flux is the vec- tor difference between the two fluxes. At 55 Hz, the resultant flux leads the armature flux by an angle that is slightly larger than 90°, as shown in Figure 11–28A.

The torque due to the resultant flux acting on the iron vane is proportional to the product of the armature flux and the in-phase component of the resultant field flux. The direction of the torque in Figure 11–28A causes the pointer to move downscale.

This deflection of the movement causes the iron vane to move out of alignment with the field flux. A countertorque is developed as the vane flux and the field flux align them- selves to obtain the shortest possible flux path. When the countertorque equals the armature coil torque, the pointer comes to rest.

Increasing Frequency. With a higher frequency, the leading current (I ) increases and its phase angle with the line voltage decreases. The lagging current (I ) decreases and its phase angle with the line voltage increases. As a result, the phase angle between the

terminal voltage and the resultant field flux also decreases, as does the phase angle between the armature current and the applied voltage.

Figure 11–28B represents a condition in which the two field currents are equal. These currents have equal and opposite phase angles with the applied voltage. The armature cur- rent is in phase with the applied voltage. The resultant of the two field fluxes is 90° out of phase with the voltage. Therefore, the in-phase component of the field flux is zero and there is no deflecting torque. The field flux aligns the iron vane so that the pointer is held at midscale.

If the frequency increases even more, the leading current increases and its phase angle with the applied voltage decreases. The lagging current in the other circuit decreases and has a larger phase angle with the applied voltage. The armature current now lags the applied voltage, as shown in Figure 11–28C. The in-phase component of the resultant field flux is now in the opposite direction. The resulting torque causes the pointer to move upscale.

Resonant-type frequency meters are usually designed to operate on single-phase 115- or 120-V circuits. If the meter scale has a range of 55–60–65 Hz, the meter will indicate frequency values to an accuracy of 0.15 Hz.

RECORDING INSTRUMENTS

Many applications require that the conditions existing in an electrical circuit be monitored constantly. However, it is uneconomical to assign a person to record instrument readings repeatedly. To overcome this problem, recording instruments are used. Such instruments provide a graphical record of the actual circuit conditions at any time. Recording instruments may be grouped into two broad categories:

1. Instruments to record electrical values, such as volts, amperes, watts, power factor, and frequency.

2. Instruments to record nonelectrical quantities. For example, a temperature recorder uses a potentiometer system to record the output of a thermocouple.

Recording instruments are similar to indicating instruments in many ways. They use a permanent-magnet, moving-coil-type construction for dc circuits. For ac circuits, recording instruments may use either the moving iron or the dynamometer-type con- struction. Whereas the pointer of an indicating instrument just shows the measured quantity on a fixed scale, a recording instrument provides a permanent graphical record. The measured quantities are drawn on a scaled paper chart as it moves past a pen at a constant speed. Because of the friction between the pen and the chart, the indicating movement must have a higher torque than is required in an indicating instrument. As a result, recording instruments are larger and require more power to operate than is required by indicating instruments of the same scale range. Recording instruments are also more highly damped than are indicating instruments so that the pen does not overshoot the chart.

Strip-Chart Recorder

The strip-chart recorder is the most commonly used graphical recording instrument. The permanent record of measurements is made on a strip of paper 4 to 6 in. wide and up to 60 ft long. Figure 11–29 shows an ac recording voltmeter. This strip-chart-type voltmeter has several advantages over nonrecording voltmeters. The long charts allow the record to cover a considerable amount of time. This means that a minimum of operator attention is required. The chart can be operated at a relatively high speed to provide a detailed graphical record.

The principal parts of a strip-chart recording instrument are

1. the frame supporting the various parts of the instrument.

2. the system that moves according to variations in the quantity being measured.

3. the chart carriage, consisting of the chart, the clock mechanism, the timing gears and drum, the chart spool, and the reroll mechanism.

4. the fixed scale on which the value of the quantity being recording is indicated.

5. the recording system, consisting of a special pen-and-ink reservoir or an inkless marking system.

The same basic types of moving systems are used in both graphical recording instruments and indicating instruments. A permanent-magnet moving coil mechanism is shown in Figure 11–30. This mechanism is used with a dc recording instrument to overcome the friction between the pen and the chart. The pen in this movement is carefully counterbalanced. A repulsion-vane moving system for an ac recording ammeter is shown in Figure 11–31A. Figure 11–31B illustrates a two-element electrodynamometer mechanism for a three-phase recording wattmeter.

Chart and Drum. The graphical record is drawn on a chart that is graduated (scaled) in two directions. One of these scales corresponds to the scale range of the instrument. The second scale represents hours, minutes, or seconds, depending on the clock mechanism and the timing gears of the chart carriage. The timescale is uniformly spaced for a constant chart speed, which is provided by the drive mechanism. The drive for the timing drum may be a synchronous electric clock, a conventional hand-wound spring clock, or a spring-type clock mechanism wound by a small electric motor. The last drive listed provides the convenience of an electric drive. Also, it guarantees that a power failure will not stop the chart motion until the spring runs down.

The friction between the chart and the pen requires that the pen drive mechanism have a greater torque than in a simple indicating instrument. The larger instrument movements are costly and take a great deal of power from the circuit being measured. The amount of power required can be reduced by using electronic amplifiers. Such an amplifier can drive the recorder element using less power from the circuit to be measured. Voltage and current signals can be amplified directly; the measurement of power and VARs requires special amplifiers.

Amplifiers. One type of amplifier used for power and VARs measurements is a photo- electric device. This device uses conventional wattmeter elements mounted on an auxiliary shaft with a reflecting mirror. An optical system with photocells and electronic amplifiers develops a dc current proportional to the quantity to be measured. This type of amplifier has sufficient power to drive the recorder pen.

Pen Positioning. Many recorders use a motor-and-gear system to position the pen. A regulating system compares the input voltage to the voltage of a precision slide-wire potentiometer (which is driven from the recorder output shaft). If the input voltage changes, the servoamplifier causes the motor to run until the pen and its attached potentiometer are positioned so that the slider voltage is equal to the signal voltage.

A recorder using this system requires very little input power from the circuit being measured. The output drive is so powerful that accessories can be added, such as auxiliary slide-wire potentiometers, limit switches, and devices to code the measured quantities into digital computer language. These accessories can operate alarms and remote devices and can supply information to digital computers.

Other accessories permit recorders to graph many different quantities on one chart. A stepping switch connects the measuring circuit to a different input at regular intervals. As soon as the pointer is positioned, the printer places a dot with a number beside it on the chart to indicate the input being measured. The stepping switch then moves to the next input, and the process is repeated. As a result, the chart contains a series of dots for each of the input signals.

Most recorders operate from a dc signal having a magnitude in millivolts. Such recorders require transducers to convert quantities such as pressure, flow, strain, ac volts, ac amperes, watts, and VARs to dc millivolt signals that can be recorded.

SYNCHROSCOPES

The synchroscope is an instrument that shows the relative phase angle and the frequency difference between two alternating voltages. This instrument indicates when alternators are in phase. It also indicates whether the frequency of the incoming generator is higher or lower than that of the generator already connected to the line.

There are a number of versions of synchroscopes available. Two commonly used synchroscopes are the polarized-vane type and the moving iron type. These synchroscopes are

designed for operation on single-phase circuits. Both devices show when the voltages of two single-phase ac generators are synchronized. They also can be used with three-phase genera- tors if the phase sequences of the generators are known.

Polarized-Vane Synchroscope

The polarized-vane synchroscope (Figure 11–24) uses a mechanism that is similar in physical structure to that of the polarized-vane power factor meter. The basic difference in this mechanism is that the polarizing coil is wound as a potential coil rather than as a current coil. The stator winding has a phase-splitting network and is connected across one phase of the incoming generator. The polarizing winding for the vanes is connected across the corresponding phase of the generator already on the line.

The stator winding of a polarized-vane synchroscope is arranged so that a two- phase field effect is obtained by a phase-splitting network, as shown in Figure 11–24.

In the stator network system, capacitor C causes current I to lead the voltage (V) by a large phase angle of 75° to 80°. Current I lags V because of the inductance of coil A. The amount of lag is about 10° to 15°. As a result, the angle between currents I is 90°.

Operation of the Polarized-Vane Synchroscope

Figure 11–25 shows the relationships between the field and vane fluxes for one cycle with the voltages of the two generators in synchronism. If the rotating field is 61 Hz and the field of the vane polarization is 60 Hz, then the rotating field is 1⁄60 th revolution ahead each time the vanes reach maximum magnetism in one polarity. The vanes line up with the position of the field at the instant of maximum vane magnetism. Thus, each complete cycle of vane polarization brings the vanes 1⁄60 th of a turn further around. For this case, the vanes make one complete revolution in one second. If the stator field rotates at 62 Hz, the vanes will rotate twice as fast. That is, they will make two revolutions in one second.

Assume that a frequency of 59 Hz is applied to the stator windings and 60 Hz is applied in the polarizing coil. The vanes will then make one revolution per second in the opposite direction. In other words, the speed of the pointer is the difference in frequency of the incoming generator and the machine already connected to the line wires. The direction of rotation of the pointer shows whether the speed of the incoming generator is too fast or too slow. When the two generators are operating at the same frequency, the vanes do not rotate. The position of the pointer for this case indicates the phase relationship between the two voltages.

FREQUENCY METERS

Electric motors, transformers, and other types of machines require the correct volt- age for efficient operation. These machines are also designed to operate at a definite frequency. In the case of electric clocks, it is very important that the frequency be accurately indicated. A variation of a small fraction of a cycle, continued through a long period of time, can result in serious errors in time indication on an electric clock. Therefore, electric power systems must operate at the correct frequency. It is obvious that frequency- indicating instruments must be used to show the frequency of a system.

Standard practice requires that ac systems operate at a single frequency. Thus, frequency indications are required to cover only a narrow band of frequency values on either side of the normal frequency. This means that the accuracy of the instrument is improved over what it would be if the instrument covered a wide frequency range.

Resonant Circuit Frequency Meter

One type of commonly used frequency meter is the resonant circuit meter. The physical structure of such a frequency meter resembles that of the dynamometer.

A schematic diagram of a resonant circuit frequency meter is shown in Figure 11–26. The use of two series resonant circuits provides a deflecting torque that has a definite relationship to the applied voltage regardless of its magnitude. The two field coils are alike and are connected so that their fluxes oppose each other. Each field coil is

connected in series with an inductor–capacitor combination. The constants of this combination permit series resonance below the normal operating frequency in one field coil and series resonance above the normal frequency in the other field coil. If a frequency meter is designed to operate on a normal frequency at 60 Hz, the field circuits are designed so that they are in resonance at 45 Hz and 75 Hz. The armature coil is connected through lead-in spirals. It has almost no countertorque effects and carries the total current of both field circuits.

Changing Circuit Impedance. The change in the circuit impedance of each field coil circuit with a change in frequency is shown in Figure 11–27. Figure 11–27B shows the currents in each of the field circuits and the total armature current. The magnitudes of these currents vary with frequency. Within the operating range of the frequency, the curves show that the impedance of the circuit resonating at 45 Hz is inductive. For the circuit resonating at 75 Hz, the impedance is capacitive. This means that the current in field coil F in circuit A always lags the terminal voltage. Also, the current in field coil F in circuit B always leads the voltage. The actual value of lag or lead and the magnitude of the current in each circuit all depend on the frequency. The current in the armature is the vector sum of the two field currents. Both the armature current and the armature flux lead or lag the terminal voltage, depending on which field current is greater. When the frequency is such that the leading and lagging currents are equal, the armature current is in phase with the terminal voltage.

Field Flux

The fluxes of the field coils oppose each other. Thus, the resultant field flux is the vec- tor difference between the two fluxes. At 55 Hz, the resultant flux leads the armature flux by an angle that is slightly larger than 90°, as shown in Figure 11–28A.

The torque due to the resultant flux acting on the iron vane is proportional to the product of the armature flux and the in-phase component of the resultant field flux. The direction of the torque in Figure 11–28A causes the pointer to move downscale.

This deflection of the movement causes the iron vane to move out of alignment with the field flux. A countertorque is developed as the vane flux and the field flux align them- selves to obtain the shortest possible flux path. When the countertorque equals the armature coil torque, the pointer comes to rest.

Increasing Frequency. With a higher frequency, the leading current (I ) increases and its phase angle with the line voltage decreases. The lagging current (I ) decreases and its phase angle with the line voltage increases. As a result, the phase angle between the

terminal voltage and the resultant field flux also decreases, as does the phase angle between the armature current and the applied voltage.

Figure 11–28B represents a condition in which the two field currents are equal. These currents have equal and opposite phase angles with the applied voltage. The armature cur- rent is in phase with the applied voltage. The resultant of the two field fluxes is 90° out of phase with the voltage. Therefore, the in-phase component of the field flux is zero and there is no deflecting torque. The field flux aligns the iron vane so that the pointer is held at midscale.

If the frequency increases even more, the leading current increases and its phase angle with the applied voltage decreases. The lagging current in the other circuit decreases and has a larger phase angle with the applied voltage. The armature current now lags the applied voltage, as shown in Figure 11–28C. The in-phase component of the resultant field flux is now in the opposite direction. The resulting torque causes the pointer to move upscale.

Resonant-type frequency meters are usually designed to operate on single-phase 115- or 120-V circuits. If the meter scale has a range of 55–60–65 Hz, the meter will indicate frequency values to an accuracy of 0.15 Hz.

RECORDING INSTRUMENTS

Many applications require that the conditions existing in an electrical circuit be monitored constantly. However, it is uneconomical to assign a person to record instrument readings repeatedly. To overcome this problem, recording instruments are used. Such instruments provide a graphical record of the actual circuit conditions at any time. Recording instruments may be grouped into two broad categories:

1. Instruments to record electrical values, such as volts, amperes, watts, power factor, and frequency.

2. Instruments to record nonelectrical quantities. For example, a temperature recorder uses a potentiometer system to record the output of a thermocouple.

Recording instruments are similar to indicating instruments in many ways. They use a permanent-magnet, moving-coil-type construction for dc circuits. For ac circuits, recording instruments may use either the moving iron or the dynamometer-type con- struction. Whereas the pointer of an indicating instrument just shows the measured quantity on a fixed scale, a recording instrument provides a permanent graphical record. The measured quantities are drawn on a scaled paper chart as it moves past a pen at a constant speed. Because of the friction between the pen and the chart, the indicating movement must have a higher torque than is required in an indicating instrument. As a result, recording instruments are larger and require more power to operate than is required by indicating instruments of the same scale range. Recording instruments are also more highly damped than are indicating instruments so that the pen does not overshoot the chart.

Strip-Chart Recorder

The strip-chart recorder is the most commonly used graphical recording instrument. The permanent record of measurements is made on a strip of paper 4 to 6 in. wide and up to 60 ft long. Figure 11–29 shows an ac recording voltmeter. This strip-chart-type voltmeter has several advantages over nonrecording voltmeters. The long charts allow the record to cover a considerable amount of time. This means that a minimum of operator attention is required. The chart can be operated at a relatively high speed to provide a detailed graphical record.

The principal parts of a strip-chart recording instrument are

1. the frame supporting the various parts of the instrument.

2. the system that moves according to variations in the quantity being measured.

3. the chart carriage, consisting of the chart, the clock mechanism, the timing gears and drum, the chart spool, and the reroll mechanism.

4. the fixed scale on which the value of the quantity being recording is indicated.

5. the recording system, consisting of a special pen-and-ink reservoir or an inkless marking system.

The same basic types of moving systems are used in both graphical recording instruments and indicating instruments. A permanent-magnet moving coil mechanism is shown in Figure 11–30. This mechanism is used with a dc recording instrument to overcome the friction between the pen and the chart. The pen in this movement is carefully counterbalanced. A repulsion-vane moving system for an ac recording ammeter is shown in Figure 11–31A. Figure 11–31B illustrates a two-element electrodynamometer mechanism for a three-phase recording wattmeter.

Chart and Drum. The graphical record is drawn on a chart that is graduated (scaled) in two directions. One of these scales corresponds to the scale range of the instrument. The second scale represents hours, minutes, or seconds, depending on the clock mechanism and the timing gears of the chart carriage. The timescale is uniformly spaced for a constant chart speed, which is provided by the drive mechanism. The drive for the timing drum may be a synchronous electric clock, a conventional hand-wound spring clock, or a spring-type clock mechanism wound by a small electric motor. The last drive listed provides the convenience of an electric drive. Also, it guarantees that a power failure will not stop the chart motion until the spring runs down.

The friction between the chart and the pen requires that the pen drive mechanism have a greater torque than in a simple indicating instrument. The larger instrument movements are costly and take a great deal of power from the circuit being measured. The amount of power required can be reduced by using electronic amplifiers. Such an amplifier can drive the recorder element using less power from the circuit to be measured. Voltage and current signals can be amplified directly; the measurement of power and VARs requires special amplifiers.

Amplifiers. One type of amplifier used for power and VARs measurements is a photo- electric device. This device uses conventional wattmeter elements mounted on an auxiliary shaft with a reflecting mirror. An optical system with photocells and electronic amplifiers develops a dc current proportional to the quantity to be measured. This type of amplifier has sufficient power to drive the recorder pen.

Pen Positioning. Many recorders use a motor-and-gear system to position the pen. A regulating system compares the input voltage to the voltage of a precision slide-wire potentiometer (which is driven from the recorder output shaft). If the input voltage changes, the servoamplifier causes the motor to run until the pen and its attached potentiometer are positioned so that the slider voltage is equal to the signal voltage.

A recorder using this system requires very little input power from the circuit being measured. The output drive is so powerful that accessories can be added, such as auxiliary slide-wire potentiometers, limit switches, and devices to code the measured quantities into digital computer language. These accessories can operate alarms and remote devices and can supply information to digital computers.

Other accessories permit recorders to graph many different quantities on one chart. A stepping switch connects the measuring circuit to a different input at regular intervals. As soon as the pointer is positioned, the printer places a dot with a number beside it on the chart to indicate the input being measured. The stepping switch then moves to the next input, and the process is repeated. As a result, the chart contains a series of dots for each of the input signals.

Most recorders operate from a dc signal having a magnitude in millivolts. Such recorders require transducers to convert quantities such as pressure, flow, strain, ac volts, ac amperes, watts, and VARs to dc millivolt signals that can be recorded.

TWO-ELEMENT WATTMETER FOR THREE-PHASE SYSTEM

Unit 10 described power measurement in three-phase circuit systems. Recall that two single-phase wattmeters were used to measure the power in a three-phase, three-wire sys- tem. The two single-phase wattmeters can be combined into a single instrument. The scale of this instrument indicates the sum or difference of the power values indicated by the separate meters. To make the single wattmeter, two sets of potential coils are mounted on a single shaft. Also, two sets of field coils are mounted on the instrument frame so that they have the proper relationship to the armature coils. In this way, each of two power measuring mechanisms develops a torque that is proportional to the power in the circuit to which it is connected. These torque values are added to obtain the total power in the three-phase, three-wire circuit.

If the power factor of the system is less than 0.5, the torque of one mechanism opposes that of the second mechanism. The difference between the torque values is the power indication.

A wattmeter containing two dynamometer mechanisms (Figure 11–15) is called a two-element wattmeter.

In Figure 11–16, a two-element wattmeter is shown connected into a three-phase circuit. The current and potential terminals are shown on the instrument case for both elements. Note that the connections shown in Figures 11–15 and 11–16 are the same as the connections given for the two-wattmeter method described in Unit 10.

VARMETERS

The previous section showed how the dynamometer-type mechanism is used to mea- sure true power in watts. This same instrument can also be used to measure the reactive volt-amperes (VARs) in an ac circuit. In this use, the instrument is known as a varmeter. The wattmeter indicates the product of the circuit voltage and the in-phase component of the current. The varmeter indicates the product of the circuit voltage and the current component 90° out of phase with the voltage.

To measure VARs, the phase of the potential coil voltage must be shifted by 90°. The flux of the potential coil is then in phase with the flux due to the quadrature component of current in the stationary coil. The phase shift in a single-phase circuit is obtained by connecting an external impedance in series with the potential coil. In this way, the current in the movable coils lags the voltage by 90°.

Measurement of VARs in a Three-Phase Circuit

To find the VARs in a three-phase circuit, a two-element varmeter is used. This device has the same construction as a two-element wattmeter. However, as shown in Figure 11–17, an external phase-shifting autotransformer is added to the varmeter to shift the potential coil voltages 90 electrical degrees.

In Figures 11–17 and 11–18, voltages 1–2 and 3–2 are applied to the transformer from the three-phase line. Taps on the autotransformer are selected as follows:

 

POWER FACTOR METERS

The power factor of a circuit can be determined by taking simultaneous readings with a wattmeter, an ammeter, and a voltmeter. However, this method is too inconvenient to be used when the power factor of a system is to be determined repeatedly. The task is

simplified by the use of a power factor meter. Any deflection of the meter pointer indicates the ratio of the power in watts to the apparent power in volt-amperes. The instrument also shows whether the current is lagging, or leading, the voltage.

Single-Phase Power Factor Meter

A single-phase power factor meter resembles a single-phase wattmeter. The stationary field coils are connected in series with one side of the line. The field coils carry the line current and produce the field flux. The single-phase power factor meter differs from the wattmeter in that it has no control springs. The moving coil, or armature construction, is also different in the power factor meter. The moving mechanism has two armature coils. These coils are mounted on the same shaft. The axes of the coils are 90° apart. One moving coil is connected across the line with a noninductive resistance in series. The flux of this coil reacts with that of the field coil to produce a torque that is proportional to the in-phase component of current. The other moving coil is connected across the line and has an inductive reactance in series with it. The current in this coil lags the line voltage by almost 90°. Thus, the torque for this coil is proportional to the line current component, which is 90° out of phase with the line voltage.

Crossed-Coil Power Factor Meter

A schematic diagram of a single-phase power factor meter is shown in Figure 11–20. This meter is called a crossed-coil power factor meter because the two moving coils are crossed at a 90° angle. A cutaway view of the mechanism of a crossed-coil power factor meter is shown in Figure 11–21.

When this type of meter is connected into a circuit containing a noninductive unity power factor load, the entire line current is in phase with the voltage. This means that full torque is developed by the moving coil. The voltage of this coil is in phase with the line current. The quadrature component of current at unity power factor is zero. Thus, torque is not developed by the moving coil whose current lags the line voltage by 90°. As a result, the mechanism moves to a position where the flux alignment between the field current and the active moving coil is at a maximum. The pointer then indicates a power factor of unity, or 1.00.

Assume that the meter shown in Figure 11–21 is connected to a circuit having a power factor less than unity. The movable coil is in series with the inductive reactance. This coil develops torque in a direction determined by the lagging or leading quadrature current

component in the fixed field coils. The torque magnitude is determined by the amount of quadrature current. A torque is also created by the in-phase component of current opposing the torque caused by the quadrature current. The resultant of these two torques determines the final position of the pointer. As a result, control springs are not required. The pointer position shows the lagging or leading power factor value.

Another form of the crossed-coil power factor meter is shown in Figure 11–22. In this meter, separate elements are used for the in-phase current and the quadrature potential current.

Three-Phase Meter

The crossed-coil power factor meter designed for three-phase service is similar in appearance and structure to the single-phase meter. However, the operating principle of the three-phase meter is different. In the three-phase meter, the crossed coils of the moving mechanism are connected in series with resistors across two phases. The connections are made so that the torques of the two coils oppose each other. The stationary field coil (current coil) is connected in series with one phase leg. The two potential coils are energized from two phases common to the line wire in which the field coil or current coil is connected.

Figure 11–23 is a schematic diagram of the connections for a three-phase, crossed-coil power factor meter. The potential coils are placed at an angle of 60° with each other. For a balanced load, power factor variations change the phase angle between the field coil cur- rent and the two potential coil currents. Thus, one phase angle increases and the other angle decreases. Therefore, the torque of one part of the element is proportional to the cosine of 30°, plus the circuit phase angle. The torque of the other part of the element is the cosine of 30°, minus the circuit phase angle. The deflection shown by the meter actually varies by the ratio of the readings that would be given by separate single-phase wattmeters connected in corresponding phases. This ratio can be calibrated directly as the power factor.

TWO-ELEMENT WATTMETER FOR THREE-PHASE SYSTEM

Unit 10 described power measurement in three-phase circuit systems. Recall that two single-phase wattmeters were used to measure the power in a three-phase, three-wire sys- tem. The two single-phase wattmeters can be combined into a single instrument. The scale of this instrument indicates the sum or difference of the power values indicated by the separate meters. To make the single wattmeter, two sets of potential coils are mounted on a single shaft. Also, two sets of field coils are mounted on the instrument frame so that they have the proper relationship to the armature coils. In this way, each of two power measuring mechanisms develops a torque that is proportional to the power in the circuit to which it is connected. These torque values are added to obtain the total power in the three-phase, three-wire circuit.

If the power factor of the system is less than 0.5, the torque of one mechanism opposes that of the second mechanism. The difference between the torque values is the power indication.

A wattmeter containing two dynamometer mechanisms (Figure 11–15) is called a two-element wattmeter.

In Figure 11–16, a two-element wattmeter is shown connected into a three-phase circuit. The current and potential terminals are shown on the instrument case for both elements. Note that the connections shown in Figures 11–15 and 11–16 are the same as the connections given for the two-wattmeter method described in Unit 10.

VARMETERS

The previous section showed how the dynamometer-type mechanism is used to mea- sure true power in watts. This same instrument can also be used to measure the reactive volt-amperes (VARs) in an ac circuit. In this use, the instrument is known as a varmeter. The wattmeter indicates the product of the circuit voltage and the in-phase component of the current. The varmeter indicates the product of the circuit voltage and the current component 90° out of phase with the voltage.

To measure VARs, the phase of the potential coil voltage must be shifted by 90°. The flux of the potential coil is then in phase with the flux due to the quadrature component of current in the stationary coil. The phase shift in a single-phase circuit is obtained by connecting an external impedance in series with the potential coil. In this way, the current in the movable coils lags the voltage by 90°.

Measurement of VARs in a Three-Phase Circuit

To find the VARs in a three-phase circuit, a two-element varmeter is used. This device has the same construction as a two-element wattmeter. However, as shown in Figure 11–17, an external phase-shifting autotransformer is added to the varmeter to shift the potential coil voltages 90 electrical degrees.

In Figures 11–17 and 11–18, voltages 1–2 and 3–2 are applied to the transformer from the three-phase line. Taps on the autotransformer are selected as follows:

 

POWER FACTOR METERS

The power factor of a circuit can be determined by taking simultaneous readings with a wattmeter, an ammeter, and a voltmeter. However, this method is too inconvenient to be used when the power factor of a system is to be determined repeatedly. The task is

simplified by the use of a power factor meter. Any deflection of the meter pointer indicates the ratio of the power in watts to the apparent power in volt-amperes. The instrument also shows whether the current is lagging, or leading, the voltage.

Single-Phase Power Factor Meter

A single-phase power factor meter resembles a single-phase wattmeter. The stationary field coils are connected in series with one side of the line. The field coils carry the line current and produce the field flux. The single-phase power factor meter differs from the wattmeter in that it has no control springs. The moving coil, or armature construction, is also different in the power factor meter. The moving mechanism has two armature coils. These coils are mounted on the same shaft. The axes of the coils are 90° apart. One moving coil is connected across the line with a noninductive resistance in series. The flux of this coil reacts with that of the field coil to produce a torque that is proportional to the in-phase component of current. The other moving coil is connected across the line and has an inductive reactance in series with it. The current in this coil lags the line voltage by almost 90°. Thus, the torque for this coil is proportional to the line current component, which is 90° out of phase with the line voltage.

Crossed-Coil Power Factor Meter

A schematic diagram of a single-phase power factor meter is shown in Figure 11–20. This meter is called a crossed-coil power factor meter because the two moving coils are crossed at a 90° angle. A cutaway view of the mechanism of a crossed-coil power factor meter is shown in Figure 11–21.

When this type of meter is connected into a circuit containing a noninductive unity power factor load, the entire line current is in phase with the voltage. This means that full torque is developed by the moving coil. The voltage of this coil is in phase with the line current. The quadrature component of current at unity power factor is zero. Thus, torque is not developed by the moving coil whose current lags the line voltage by 90°. As a result, the mechanism moves to a position where the flux alignment between the field current and the active moving coil is at a maximum. The pointer then indicates a power factor of unity, or 1.00.

Assume that the meter shown in Figure 11–21 is connected to a circuit having a power factor less than unity. The movable coil is in series with the inductive reactance. This coil develops torque in a direction determined by the lagging or leading quadrature current

component in the fixed field coils. The torque magnitude is determined by the amount of quadrature current. A torque is also created by the in-phase component of current opposing the torque caused by the quadrature current. The resultant of these two torques determines the final position of the pointer. As a result, control springs are not required. The pointer position shows the lagging or leading power factor value.

Another form of the crossed-coil power factor meter is shown in Figure 11–22. In this meter, separate elements are used for the in-phase current and the quadrature potential current.

Three-Phase Meter

The crossed-coil power factor meter designed for three-phase service is similar in appearance and structure to the single-phase meter. However, the operating principle of the three-phase meter is different. In the three-phase meter, the crossed coils of the moving mechanism are connected in series with resistors across two phases. The connections are made so that the torques of the two coils oppose each other. The stationary field coil (current coil) is connected in series with one phase leg. The two potential coils are energized from two phases common to the line wire in which the field coil or current coil is connected.

Figure 11–23 is a schematic diagram of the connections for a three-phase, crossed-coil power factor meter. The potential coils are placed at an angle of 60° with each other. For a balanced load, power factor variations change the phase angle between the field coil cur- rent and the two potential coil currents. Thus, one phase angle increases and the other angle decreases. Therefore, the torque of one part of the element is proportional to the cosine of 30°, plus the circuit phase angle. The torque of the other part of the element is the cosine of 30°, minus the circuit phase angle. The deflection shown by the meter actually varies by the ratio of the readings that would be given by separate single-phase wattmeters connected in corresponding phases. This ratio can be calibrated directly as the power factor.

AMMETERS AND VOLTMETERS

Ammeters and voltmeters of the same type operate on the same basic principle. The main difference is that ammeter movements have a few turns of heavy wire and voltmeter movements have many turns of fine wire. Voltmeters also have resistors connected in series with the movement to obtain the desired ranges.

PRACTICAL RANGES FOR MOVING IRON INSTRUMENTS

AC Ammeters

The physical size of ac ammeters, using any type of moving iron movement, deter- mines the current rating of the instrument. The size of the instrument is influenced by the amount of heat to be dissipated and the size of the connection terminals to be supported. In small panel instruments, 100 A is the maximum practical current rating. For large portable instruments, 200 A is the maximum rating. In some large ammeters designed for switch- board use, the current rating may be as high as 600 A.

Larger Current Ratings. Other means must be used to obtain larger current ratings for moving iron ac ammeters. Permanent-magnet moving coil instruments commonly use shunts to obtain higher current ratings. However, shunts are not satisfactory for moving iron instruments. One reason is that the movement is less sensitive and requires a greater voltage drop across the shunt than in dc ammeters. Thus, there is more heat dissipation in the shunt. As a result, the resistance increases in the various parts of the instrument circuit, creating errors in accuracy.

The use of a shunt for moving iron instruments also introduces frequency errors. The inductive reactance of the shunt is low and the inductive reactance of the coil is relatively high. The impedance of the shunt remains nearly unchanged over a range of frequencies. The impedance of the coil, however, changes considerably as the frequency varies. Because the changes in frequency do not affect the coil and the shunt equally, there will be a large error if the instrument is used on a frequency other than the one at which it was calibrated.

Many moving iron instruments are used only for ac measurements. As a result, it is a standard practice to use an instrument current transformer to obtain an increase in the cur- rent range of a 5-A instrument. When the measuring instrument is connected to the secondary of the transformer, the current in the transformer primary will be indicated accurately. The instrument can be calibrated to indicate the primary current. The actual calibration depends on the ratio between the primary current and the secondary current. Detailed information on instrument current transformers is given in a later unit of this text.

AC Voltmeters

When moving iron instruments are used as ac voltmeters, series resistors are used to extend the scale range for voltages up to 750 V. The effect is the same as that obtained when a series resistor or a voltage multiplier is used with permanent-magnet moving coil movements in dc voltmeters.

When ac voltages greater than 750 V are to be measured, larger ohmic resistance values cannot be used. Because of the higher ohmic values, more power would be expended in the resistors. Also, there would be high-voltage insulation problems. Thus, large ac voltages are measured using an instrument potential transformer with the movement. The primary winding and insulation of the transformer are suitable for the higher voltage. The secondary winding is usually rated at 120 V. The ac voltmeter usually has a coil rating of 150 V. In many cases, the instrument scale is calibrated to indicate the primary voltage directly. Detailed information on instrument potential transformers is given in a later unit of this text.

THE DYNAMOMETER WATTMETER

To measure the power in watts with an instrument having a dynamometer movement, the stationary field coils are connected in series with the line. Thus, the field flux depends on the current. The moving coils are connected across the line so that the moving coil flux is proportional to the system voltage. Figure 11–10 shows a typical wattmeter circuit. The resistor is connected in series with the moving coil. It can be shown that the instantaneous torque is proportional to the product of the instantaneous field current and the instantaneous moving coil voltage. The average torque for a whole cycle is proportional to the average of the power pulses. This means that the pointer deflection is proportional to the power as expressed by the following equation:

Operation of the Dynamometer Wattmeter

The operation of the dynamometer wattmeter is shown by the wave patterns in Figure 11–11. In Figure 11–11A, the current, voltage, and power waves are shown for one cycle when the current and voltage are in phase. Note that the power curve at any instant is positive. When the current and voltage are in phase, the field flux and the armature flux increase and decrease together. These quantities reach their maximum values at the same time. The deflection of the movement pointer represents the average of the product of the instantaneous voltage and current. This value is the true power, in watts, for the circuit.

Figure 11–11B shows the current, voltage, and power relationships for a circuit where the current lags the voltage by 30°. In this case, the field flux and the armature flux do not reach their maximum values at the same time. The field flux reaches its maximum value 30° behind the maximum value of armature flux. This means that the torque never reaches as high a value as in the case where the current and voltage are in phase. Instead, the torque always has an average value corresponding to the product of the voltage, current, and power factor. Figure 11–11B shows that the average value of the power is less than the value shown in Figure 11–11A for the condition of the current and voltage in phase.

In Figure 11–11C, the current, voltage, and power are shown for a circuit where the current leads the voltage by 30°. The wattmeter indication is the same for this case as for the lagging current condition. Again, the average torque on the movement of the instrument is determined by the product of the instantaneous current and voltage values. Therefore, Figure 11–11C shows that the average value of the power is less than the value shown in Figure 11–11A for the condition of the current and voltage in phase.

Connecting a Dynamometer Wattmeter

When connecting an instrument having a dynamometer movement, the technician must consider the instantaneous direction of current in each of the coils. This direction determines the flux, which, in turn, specifies the direction of the deflecting torque.

The diagram in Figure 11–12 shows the marking (±) next to one of the terminals of

the potential coil circuit (the armature) and also one of the terminals of the current coil (the field). These terminals are connected to the same side of the line to ensure that the deflec- tion has the correct direction.

There are two different methods of connecting the potential coil of a wattmeter. In Figure 11–12, the potential circuit of the wattmeter is not connected directly across the load. Instead, it measures a voltage higher than the load voltage by an amount equal to the voltage drop in the current coil. In other words, the wattmeter indicates too high a value of watts. The extra power is that expended in the current coil. For the connections shown in Figure 11–12, the true power of this circuit is

True power = wattmeter reading – I² R of current coil

A second method of connecting the wattmeter is shown in Figure 11–13. In this dia- gram, the potential coil is connected directly across the load voltage. The current coil of the wattmeter now reads both the potential coil current and the load current. This reading is due to the fact that the potential coil is really a high-resistance load in parallel with the actual load. In summary, the wattmeter indicates a value that is higher than the actual power taken by the load. The power in excess of that taken by the load is equal to the power expended in the potential circuit of the wattmeter. Using the connections in Figure 11–13, the true power is

For either connection (Figures 11–12 and 11–13) the wattmeter indicates a value slightly larger than the true power. However, using the connections in Figure 11–13, the percentage error will be slightly less because the potential coil circuit is connected directly across the load.

Using a Wattmeter

To use a wattmeter, the rating of its potential coil and current coil must correspond to the current and voltage ratings of the circuit in which the instrument is to be used. For example, a wattmeter may be used in an ac circuit having a low power factor. The wattmeter can indicate a power value within the scale range of the instrument even though the current coil is greatly overloaded. Even if the circuit has a high power factor, the load current may be much larger than the current coil rating. However, because of a low voltage, the watt- meter pointer is on scale. Again, the voltage across the potential coil may be excessive. But the presence of a low current means that the power indication of the wattmeter is on scale. A wattmeter is always rated according to its potential and current coil ratings rather than in watts.

Figure 11–14 shows a voltmeter, an ammeter, and a wattmeter connected into a single-phase circuit. The voltmeter and ammeter readings will show whether the voltage or current rating of the wattmeter is exceeded. Dynamometer type wattmeters are very

expensive to produce because they must contain a stationary coil for measuring current and a moving coil for measuring voltage. Electronic type wattmeters are rapidly replacing the dynamometer type. Electronic wattmeters employ an electronic circuit to measure the quantities of voltage and current, and supply this information to a common meter movement

or digital readout. Electronic wattmeters are connected into the circuit in the same manner as a dynamometer type wattmeter.

AMMETERS AND VOLTMETERS

Ammeters and voltmeters of the same type operate on the same basic principle. The main difference is that ammeter movements have a few turns of heavy wire and voltmeter movements have many turns of fine wire. Voltmeters also have resistors connected in series with the movement to obtain the desired ranges.

PRACTICAL RANGES FOR MOVING IRON INSTRUMENTS

AC Ammeters

The physical size of ac ammeters, using any type of moving iron movement, deter- mines the current rating of the instrument. The size of the instrument is influenced by the amount of heat to be dissipated and the size of the connection terminals to be supported. In small panel instruments, 100 A is the maximum practical current rating. For large portable instruments, 200 A is the maximum rating. In some large ammeters designed for switch- board use, the current rating may be as high as 600 A.

Larger Current Ratings. Other means must be used to obtain larger current ratings for moving iron ac ammeters. Permanent-magnet moving coil instruments commonly use shunts to obtain higher current ratings. However, shunts are not satisfactory for moving iron instruments. One reason is that the movement is less sensitive and requires a greater voltage drop across the shunt than in dc ammeters. Thus, there is more heat dissipation in the shunt. As a result, the resistance increases in the various parts of the instrument circuit, creating errors in accuracy.

The use of a shunt for moving iron instruments also introduces frequency errors. The inductive reactance of the shunt is low and the inductive reactance of the coil is relatively high. The impedance of the shunt remains nearly unchanged over a range of frequencies. The impedance of the coil, however, changes considerably as the frequency varies. Because the changes in frequency do not affect the coil and the shunt equally, there will be a large error if the instrument is used on a frequency other than the one at which it was calibrated.

Many moving iron instruments are used only for ac measurements. As a result, it is a standard practice to use an instrument current transformer to obtain an increase in the cur- rent range of a 5-A instrument. When the measuring instrument is connected to the secondary of the transformer, the current in the transformer primary will be indicated accurately. The instrument can be calibrated to indicate the primary current. The actual calibration depends on the ratio between the primary current and the secondary current. Detailed information on instrument current transformers is given in a later unit of this text.

AC Voltmeters

When moving iron instruments are used as ac voltmeters, series resistors are used to extend the scale range for voltages up to 750 V. The effect is the same as that obtained when a series resistor or a voltage multiplier is used with permanent-magnet moving coil movements in dc voltmeters.

When ac voltages greater than 750 V are to be measured, larger ohmic resistance values cannot be used. Because of the higher ohmic values, more power would be expended in the resistors. Also, there would be high-voltage insulation problems. Thus, large ac voltages are measured using an instrument potential transformer with the movement. The primary winding and insulation of the transformer are suitable for the higher voltage. The secondary winding is usually rated at 120 V. The ac voltmeter usually has a coil rating of 150 V. In many cases, the instrument scale is calibrated to indicate the primary voltage directly. Detailed information on instrument potential transformers is given in a later unit of this text.

THE DYNAMOMETER WATTMETER

To measure the power in watts with an instrument having a dynamometer movement, the stationary field coils are connected in series with the line. Thus, the field flux depends on the current. The moving coils are connected across the line so that the moving coil flux is proportional to the system voltage. Figure 11–10 shows a typical wattmeter circuit. The resistor is connected in series with the moving coil. It can be shown that the instantaneous torque is proportional to the product of the instantaneous field current and the instantaneous moving coil voltage. The average torque for a whole cycle is proportional to the average of the power pulses. This means that the pointer deflection is proportional to the power as expressed by the following equation:

Operation of the Dynamometer Wattmeter

The operation of the dynamometer wattmeter is shown by the wave patterns in Figure 11–11. In Figure 11–11A, the current, voltage, and power waves are shown for one cycle when the current and voltage are in phase. Note that the power curve at any instant is positive. When the current and voltage are in phase, the field flux and the armature flux increase and decrease together. These quantities reach their maximum values at the same time. The deflection of the movement pointer represents the average of the product of the instantaneous voltage and current. This value is the true power, in watts, for the circuit.

Figure 11–11B shows the current, voltage, and power relationships for a circuit where the current lags the voltage by 30°. In this case, the field flux and the armature flux do not reach their maximum values at the same time. The field flux reaches its maximum value 30° behind the maximum value of armature flux. This means that the torque never reaches as high a value as in the case where the current and voltage are in phase. Instead, the torque always has an average value corresponding to the product of the voltage, current, and power factor. Figure 11–11B shows that the average value of the power is less than the value shown in Figure 11–11A for the condition of the current and voltage in phase.

In Figure 11–11C, the current, voltage, and power are shown for a circuit where the current leads the voltage by 30°. The wattmeter indication is the same for this case as for the lagging current condition. Again, the average torque on the movement of the instrument is determined by the product of the instantaneous current and voltage values. Therefore, Figure 11–11C shows that the average value of the power is less than the value shown in Figure 11–11A for the condition of the current and voltage in phase.

Connecting a Dynamometer Wattmeter

When connecting an instrument having a dynamometer movement, the technician must consider the instantaneous direction of current in each of the coils. This direction determines the flux, which, in turn, specifies the direction of the deflecting torque.

The diagram in Figure 11–12 shows the marking (±) next to one of the terminals of

the potential coil circuit (the armature) and also one of the terminals of the current coil (the field). These terminals are connected to the same side of the line to ensure that the deflec- tion has the correct direction.

There are two different methods of connecting the potential coil of a wattmeter. In Figure 11–12, the potential circuit of the wattmeter is not connected directly across the load. Instead, it measures a voltage higher than the load voltage by an amount equal to the voltage drop in the current coil. In other words, the wattmeter indicates too high a value of watts. The extra power is that expended in the current coil. For the connections shown in Figure 11–12, the true power of this circuit is

True power = wattmeter reading – I² R of current coil

A second method of connecting the wattmeter is shown in Figure 11–13. In this dia- gram, the potential coil is connected directly across the load voltage. The current coil of the wattmeter now reads both the potential coil current and the load current. This reading is due to the fact that the potential coil is really a high-resistance load in parallel with the actual load. In summary, the wattmeter indicates a value that is higher than the actual power taken by the load. The power in excess of that taken by the load is equal to the power expended in the potential circuit of the wattmeter. Using the connections in Figure 11–13, the true power is

For either connection (Figures 11–12 and 11–13) the wattmeter indicates a value slightly larger than the true power. However, using the connections in Figure 11–13, the percentage error will be slightly less because the potential coil circuit is connected directly across the load.

Using a Wattmeter

To use a wattmeter, the rating of its potential coil and current coil must correspond to the current and voltage ratings of the circuit in which the instrument is to be used. For example, a wattmeter may be used in an ac circuit having a low power factor. The wattmeter can indicate a power value within the scale range of the instrument even though the current coil is greatly overloaded. Even if the circuit has a high power factor, the load current may be much larger than the current coil rating. However, because of a low voltage, the watt- meter pointer is on scale. Again, the voltage across the potential coil may be excessive. But the presence of a low current means that the power indication of the wattmeter is on scale. A wattmeter is always rated according to its potential and current coil ratings rather than in watts.

Figure 11–14 shows a voltmeter, an ammeter, and a wattmeter connected into a single-phase circuit. The voltmeter and ammeter readings will show whether the voltage or current rating of the wattmeter is exceeded. Dynamometer type wattmeters are very

expensive to produce because they must contain a stationary coil for measuring current and a moving coil for measuring voltage. Electronic type wattmeters are rapidly replacing the dynamometer type. Electronic wattmeters employ an electronic circuit to measure the quantities of voltage and current, and supply this information to a common meter movement

or digital readout. Electronic wattmeters are connected into the circuit in the same manner as a dynamometer type wattmeter.

AC Instruments and Meters

MEASUREMENT OF AC QUANTITIES

The equipment used to measure ac quantities differs somewhat from the equipment used in dc measurements. This unit will describe the instruments generally used to mea- sure voltage, power factor, VARs, current, watts, frequency, and phase angle. In addition, meters will be described for measuring watt-hours, Watt-hour demand, varhours, and varhour demand.

For the instruments used to measure ac voltage, current, watts, and VARs, each movement must have three basic components:

1. A spring mechanism to produce an opposing torque; the magnitude of this torque depends on the quantity being measured.

2. A restoring spring mechanism to restore the indicator or pointer of the meter to zero after the required measurement is made. In practice, one mechanism is used to pro- duce the opposing torque and then return the indicator to zero.

3. A damping system to prevent the pointer from overshooting and excessive swinging.

If too much damping is provided, a long time is required before the pointer can reach a new reading after a change occurs in the measured quantity. The proper damping means that the pointer moves quickly and stabilizes quickly when the quantity being measured is changed. AC instruments often use electromagnetic damping. As shown in Figure 11–1, a permanent magnet induces eddy currents in some part of the instrument movement. The magnetic effect of these eddy currents opposes the motion of the pointer. Air damping is another method of controlling the motion of the pointer. In this method, a vane retards the movement of the pointer.

MEASUREMENT OF VOLTAGE AND CURRENT

Alternating current and voltage can be measured using several different types of movements. These movements vary in their ability to meet the criteria expressed in the following questions:

1. Does the instrument scale indicate RMS or average values?

2. To what value of volts or amperes must the movement respond?

3. Is the calibration of the scale linear in the useful range, or are the numbers on the scale crowded together in some important region?

4. How accurate is the instrument?

5. How much does it cost?

RECTIFIER INSTRUMENTS WITH D’ARSONVAL MOVEMENT

Direct Current Fundamentals described the d’Arsonval dc instrument movement. This movement can be used for ac measurement if a rectifier is also used.

Figure 11–2 shows a bridge-connected full-wave rectifier used with a voltmeter. (R is the series resistor normally required with a voltmeter.)

The dc d’Arsonval movement develops a torque that is proportional to the average value of the current in the moving coil. For an ac wave, only the RMS (effective) values are of interest. Thus, the ac scale is calibrated in RMS values. The RMS voltage is 1.11 times the average voltage value of a sine wave. This means that rectifier-type measuring instruments are accurate only when pure sine-wave quantities are involved. If the voltage to be measured has another type of wave shape, the instrument will give erroneous readings.

Multimeters are instruments that measure both ac and dc quantities. d’Arsonval move- ments are used in most multimeters. When used as a voltmeter, a multimeter is expected to have a high resistance linear scale and consume relatively little power. When used as an ammeter, most rectifier-type multimeters must be used in the range of microamperes or milliamperes. The full-scale readings will range from about 100 µA to 1000 mA. A multi- meter with a d’Arsonval movement is shown in Figure 11–3.

OTHER TYPES OF AC VOLTMETER AND AMMETER MOVEMENTS

Several other types of ac movements can be used in measuring instruments. These movements include the following:

• Magnetic vane attraction movement

• Inclined coil movement

• Repulsion movement

• Repulsion–attraction movement

• Dynamometer movement

All of the movements listed respond to RMS values of voltage or current.

The Magnetic Vane Attraction Movement

This type of movement has a soft iron plunger that projects into a stationary field coil (Figure 11–4). Current in the field coil produces a magnetic force that pulls the plunger deeper into the coil. The instantaneous value of this magnetic force is proportional to the square of the current in the coil. This means that the average torque turning the movement is proportional to the average, or mean, of the squares of the coil current (the RMS values).

This torque is independent of current direction. Thus, the instrument can be used for either ac or dc measurements.

The magnetic force that attracts the plunger has a minimum value when the plunger is just entering the coil. The value of the force increases rapidly as more of the soft iron vane enters the coil. This means that the numbers are crowded together at the lower end of the scale and are expanded for the high end of the scale. This type of movement is commonly used in low-cost ammeters. When a coil of many turns and a series resistor are added, this movement can be used to make voltage measurements.

Inclined Coil Movement

The Thompson inclined coil movement (Figure 11–5) is used in portable and switch- board ammeters and voltmeters. The scale of this movement is long and reasonably linear. An iron vane is free to move in a magnetic field. The vane tends to take a position parallel to the flux. Figure 11–5 shows a pair of elliptical iron vanes attached to a shaft passing through the center of the stationary field coil. If the current in the field coil is increased, an increasing force is produced, which tends to align the vanes with (parallel to) the coil flux. As a result, the shaft turns and moves the attached pointer across the scale.

Repulsion Movement

The repulsion-type movement can be used for both current and voltage measure- ments. A repulsion force is developed between two soft iron vanes that are affected by the same magnetic field (Figure 11–6). One iron vane is attached to the instrument shaft.

The other vane is mounted on the stationary field coil. When there is no current in the coil, the control spring holds the movable vane close to the fixed vane. Alternating current in the field coil magnetizes both vanes. The like poles of the vanes repel each other and create a torque. This torque turns the instrument shaft. The repulsion force between the two vanes varies according to the square of the current. This force also varies inversely as the square of the distance between the vanes. As a result, the movement has a reasonably uniform scale.

The Repulsion–Attraction Movement (Figure 11–7)

This type of movement is used for both ammeters and voltmeters. It produces more torque per watt than do any of the other ac movements included in this list. A cutaway view of the structure of the repulsion–attraction movement is shown in Figure 11–7.

The instantaneous polarities of the iron vanes are shown in Figure 11–8. The movable vane is repelled from the wide end of the middle fixed vane first. The repelling force decreases as the vane moves to the narrow end of the middle vane. An attracting force increases as the ends of the moving vane come closer to the upper and lower fixed attraction vanes. When these fixed attraction vanes have the correct size and spacing, a scale length representing 250° of angular deflection can be provided. The distribution of values along the scale is determined by the shape and separation of the vanes. Meters can be designed to broaden the scale at any point.

Dynamometer Movement

The dynamometer movement produces a torque by the interaction of magnetic fields. One field is caused by the current in a moving coil. A second field is due to the current in a stationary coil. This stationary magnetic field is not constant. It varies with the amount

of current in the stationary coils. Thus, the torque produced in this movement depends on the moving coil current and the stationary coil current. The fixed and moving coils are connected in series. The dynamometer movement can be adapted easily to make voltage measurements by adding the proper series resistor.

Figure 11–9 shows a dynamometer movement used as a voltmeter. When compared with d’Arsonval movements, the dynamometer movement is more efficient and accurate (to one-quarter of 1% or better). This type of movement is seldom used as an ammeter for the following reasons: (1) the lead-in spirals to the moving coil can carry a limited current only, (2) frequency variations influence the inductance of the coils and introduce error, and

(1) the resistance of the two coils in series may produce an undesirably high voltage drop across the shunt.

The torque is determined by changes in the stationary coil current or the movable coil current. Because of this fact, the dynamometer movement is a very useful measuring device for several other applications. Although this type of movement may be used for dc, most of its practical uses are for ac. For example, instruments with dynamometer movements are used to measure power in watts and reactive volt-amperes. Such instruments are also used to measure power factor and frequency and to indicate synchronism in ac circuits.