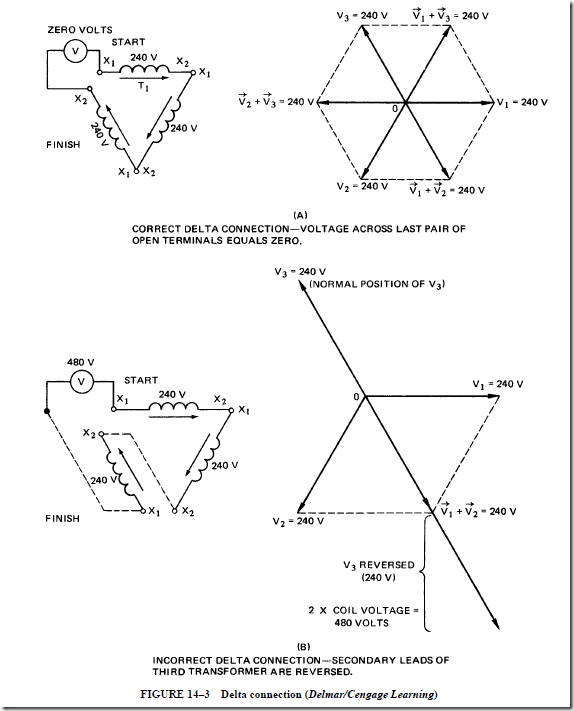
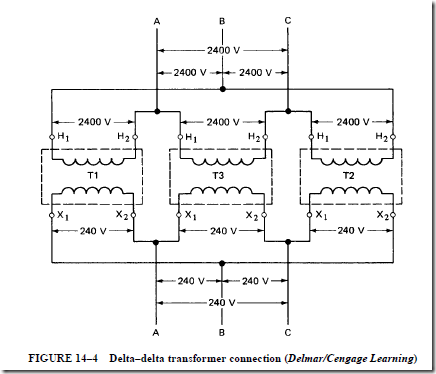
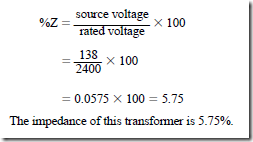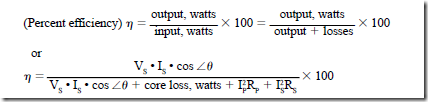TAP-CHANGING TRANSFORMERS
There is some voltage loss in high-voltage distribution circuits. This means that the impressed voltage on the primary winding of a stepdown transformer may be lower than the primary voltage indicated on the nameplate. As a result, the secondary terminal voltage is also lower than the nameplate value.
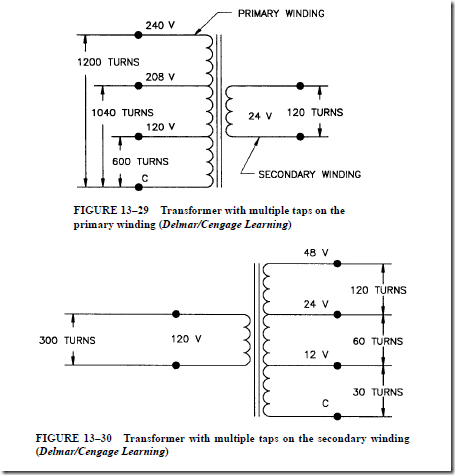
Because this condition is undesirable, provisions can be made for changing taps to obtain the voltage expected. In this way, minor adjustments can be made in the trans- former ratio to compensate for the voltage loss in the high-voltage primary line. A simple method of doing this is to bring out the tap points of the high-voltage winding to a terminal block inside the transformer. The tap connections can be changed on the terminal board to vary the number of turns of the primary winding.
Tap-Changing Switch
Figure 13–33 shows the connections for a typical tap-changing switch used with the high-voltage windings of a step down transformer. Each full coil winding on the high-volt- age side is rated at 2400 V. The voltage rating of the two coil windings in series is 4800 V. The transformer steps the voltage down to 120/240 V. The tap-changing switch contacts are shown in position 1. This means that both full coil windings are in series. If the switch is moved to position 2, section A is removed from the primary coil winding on the left, resulting in a decrease in the turns ratio between the primary and secondary windings. Thus, the secondary voltage increases. When the tap-changing switch is moved in sequence to
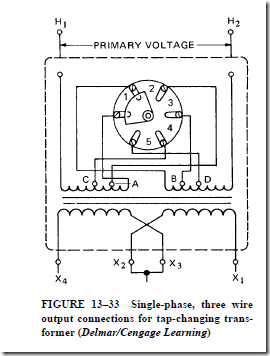
positions 3, 4, and 5, sections B, C, and D of the primary windings are removed in the same order. As each section of the primary winding is removed from the circuit, the turns ratio decreases and the secondary voltage increases.
Special tap switches, immersed in oil, are used on some large transformers. This type of switch permits the tap connections to be changed under load. In general, the tap- changing mechanism is placed in a compartment separated from the transformer tank. As a result, oil is confined near the arc-interrupting area of the tap-changing mechanism and there is no reduction in the high dielectric strength of the oil in the transformer case. A small motor drives the tap-changing mechanism. The motor is operated from a control panel.
FREQUENCY AND VOLTAGE
A transformer must be operated on an ac circuit at the frequency for which it is designed. If a lower frequency is used, the reactance of the primary winding will decrease. As a result, there will be a marked increase in the exciting current. This increase causes the flux density in the core to increase, with the result that the saturation of the core is above normal. This greater saturation causes a greater heat loss and the efficiency of the transformer is lowered. If the frequency is greater than the nameplate frequency value, the reactance will increase and the exciting current will decrease. There will be a lower flux density, but the core loss will remain nearly constant.
If the voltage is increased to a high enough value above the nameplate rating, excessive heating will take place at the windings. The flux density of the core will increase and the saturation of the core will be above normal. Transformers are designed so that they can be operated, without overheating, at a voltage that is 5% above the nameplate rating. If a transformer is operated at a voltage lower than the nameplate rating, the power output will be reduced in proportion to the reduction in voltage.
TRANSFORMER IMPEDANCE
Transformer impedance is determined by the physical construction of the trans- former. Factors such as the amount and type of core material, wire size used to con- struct the windings, the number of turns, and the degree of magnetic coupling between the windings greatly affect the transformer’s impedance. Impedance is expressed as a percent and is measured by connecting a short circuit across the low-voltage winding of the transformer and then connecting a variable voltage source to the high-voltage winding (Figure 13–34). The variable voltage is then increased until rated current flows in the low-voltage winding. The transformer impedance is determined by calculating the percentage of variable voltage as compared to the rated voltage of the high-voltage winding.
Example
Assume that the transformer shown in Figure 13–34 is a 2400/480-V, 15-kVa trans- former. To determine the impedance of the transformer, first compute the full-load current rating of the secondary winding:
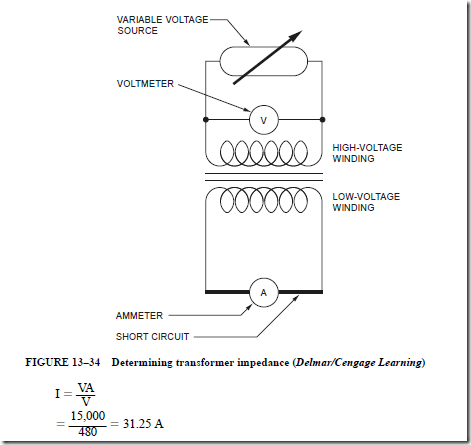
Next, increase the source voltage connected to the high-voltage winding until a current of 31.25 A flows in the low voltage winding. For the purpose of this example, assume that voltage value to be 138 V. Finally, determine the percentage of applied voltage as compared to the rated voltage:
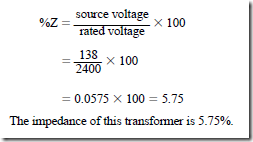
Discussion
Transformer impedance is a major factor in determining the amount of voltage drop that a transformer will exhibit between no-load and full-load conditions and in determining the amount of current flow in a short-circuit condition. Short-circuit current can be computed using the following formula:

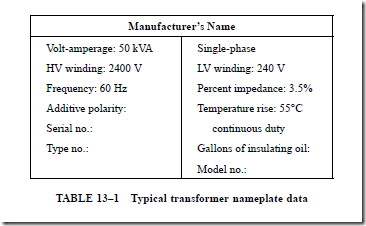
TRANSFORMER NAMEPLATE DATA
The information listed on the nameplate for a typical transformer is shown in Table 13–1. The transformer capacity is rated in kilovolt-amperes, not in kilowatts. The kilo- volt-ampere capacity is used because the load connected to the secondary determines the power factor of the output circuit of the transformer. The kVA rating represents the full-load output of the transformer, rather than the input. The nameplate also lists the voltage ratings of the high- and low-voltage windings, the frequency, the phase, the percent impedance, the polarity, the maximum temperature rise, and the gallons of trans- former oil required.
SUMMARY
• A transformer transfers energy from one ac circuit to another. This transfer is made with a change in the voltage, but with no change in the frequency.
• A transformer is a stationary device.
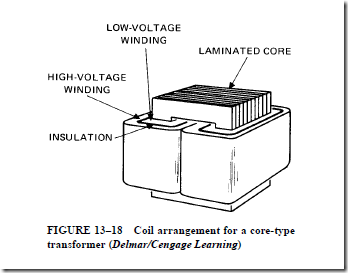
1. In its simplest form, it consists of a laminated iron core. The input and output windings are wound on this common core.
2. A transformer does not require any moving parts to transfer energy. There are no friction or windage losses and other losses are slight. Maintenance and repair costs are relatively low because of the lack of rotating parts.
• At full load, the efficiency of a transformer is between 96% and 97%. For a transformer with a very high capacity, the efficiency may be as high as 99%.
• Exciting current:
1. The exciting current is present when the primary winding of a transformer is connected to an alternating voltage source.
2. This current exists even when there is no load connected to the secondary.
3. It sets up an alternating flux in the core. This flux links the turns of both windings and induces a voltage in both windings. The total induced voltage in each winding is directly proportional to the number of turns in that winding. The alternating voltage induced in the secondary has the same frequency, but is opposite in direction to the primary winding voltage. The induced voltage in the primary winding opposes the source voltage and limits the excitation current of the primary.
• The induced voltages in the primary and secondary windings are directly proportional to the number of turns:

• Leakage flux:
1. This is a flux that does not link all of the turns of all of the coil windings.
2. This flux has its magnetic path in air and not in the core.
3. Leakage flux from the primary voltage does not link the turns of the secondary winding.
4. Leakage flux from the secondary links the secondary windings, but not the primary winding.
5. The leakage flux uses part of the impressed primary voltage to cause a reactance voltage drop; thus, both the secondary flux linkages and the secondary induced voltage are reduced.
6. Leakage flux from the secondary voltage is proportional to the secondary cur- rent; thus, there is a reactance voltage drop in the secondary winding. (Both the primary and the secondary leakage fluxes reduce the secondary terminal voltage of the transformer as the load increases.)
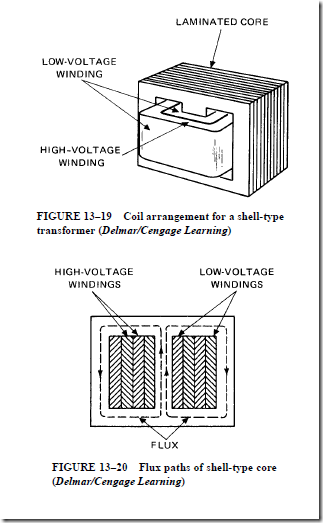
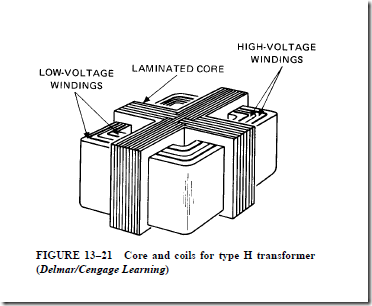
7. The leakage flux of a transformer can be controlled by the type of core used. The placement of the primary and secondary windings on the legs of the core is also a controlling factor.
• The primary current at no load is called the exciting current.
1. This current is usually 2% to 5% of the full-load current.
2. It supplies the alternating flux and the losses in the transformer core. These losses are known as core losses and consist of eddy current losses and hysteresis losses. The losses cause I2 R losses.
3. Exciting current consists of a large quadrature (magnetizing) component and a small in-phase component to supply the core losses.
4. The power factor for the exciting current is from 5% to 10% lagging.
• Voltages are induced in the metal core by the large quadrature (magnetizing) component of the exciting current.
1. Eddy currents result and circulate through the core.
a. Eddy currents can be reduced by assembling the core structure from lamination coated with insulating varnish.
b. If the laminations are not varnished, the oxide coating on each lamination still reduces the eddy current losses.
2. The core structure also has a hysteresis loss.
a. This loss is due to molecular friction or the opposition offered by the mol- ecules to changes in their direction.
b. To reduce the amount of power needed to overcome these losses, a special silicon steel is used in the core construction.
• Core losses can be measured by the core loss open-circuit test.
1. The losses of a transformer at no load are small.
2. In the open-circuit test, the voltmeter measures the primary voltage.
3. The voltmeter must be disconnected before a reading is taken with the wattmeter. This is done so that the wattmeter will not indicate the power taken by the voltmeter.
4. The wattmeter indicates the core loss in watts, and the ammeter indicates the exciting current.
5. The effective resistance of the windings of a transformer is approximately 10% more than the dc or ohmic resistance.
6. Generally, the ac or effective resistance of a transformer is obtained by measuring the dc resistance of the winding and multiplying it by 1.1.
• The efficiency of a transformer is a ratio of the output in watts to the input in watts.
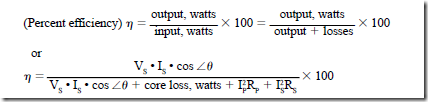
• The preferred method of determining the efficiency of a transformer is to measure the losses and add this value to the nameplate output to obtain the input.
• The impedance voltage is that voltage required to cause the rated current to flow through the impedance of the primary and secondary windings.
• The ratio of the impedance voltage to the rated terminal voltage yields the percentage impedance voltage, which is in the range of 3% to 5%.
• The voltage regulation of a transformer is the percentage change in the secondary terminal voltage from the full-load condition to the no-load condition, whereas the impressed primary voltage is held constant.
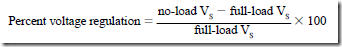
• The polarity of the transformer lead-in wires is marked according to a standard developed by the American Standards Association (ASA).
1. The high-voltage winding leads are marked H1 and H2 . H1 is on the left-hand side when the transformer is faced from the low-voltage side.
2. The low-voltage winding leads are marked X1 and X2 .
3. When H is instantaneously positive, X1 is also instantaneously positive.
4.In a transformer with subtractive polarity, the H1 and X1 leads are adjacent or directly across from each other.
5. In a transformer with additive polarity, the H and X leads are diagonally across from each other.
• If paralleled transformers are to deliver an output that is proportional to the kVA ratings
1. the percentage impedance values of each transformer must be the same.
2. the secondary terminal voltages must be the same.
3. the instantaneous polarity of the secondary leads of each transformer must be correct.
• If it is impossible to identify the transformer leads because the identifying tags are missing or disfigured, a standard test procedure can be used to determine the polarity markings.
1. In this test, a jumper lead is temporarily connected between the high-voltage lead and the low-voltage lead directly across from it.
2. A voltmeter is connected from the other high-voltage lead to the second low- voltage lead.
3. If the voltmeter reads the sum of the primary input voltage and the secondary volt- age, the transformer has additive polarity.
4. If the voltmeter reads the primary input voltage minus the secondary voltage, the transformer has subtractive polarity.
5. There is a hazard involved in making the test at high-voltage values. Thus, a test using a relatively low voltage was developed to determine transformer polarity.
• NEMA and ASA standards for transformers:
1. Additive polarity shall be standard for single-phase transformers up to 200 kVA, and having voltage ratings not in excess of 9000 V.
2. Subtractive polarity shall be standard for all single-phase transformers larger than 200 kVA, regardless of the voltage rating.
3. Subtractive polarity shall be standard for all single-phase transformers in sizes of 200 kVA and below, having high-voltage ratings above 9000 V.
• When stepdown transformers are operated in parallel, it may be necessary to remove one from service for repairs.
1. The low-voltage side of the transformer is always disconnected from the line wires before the primary fuses are opened.
2. A sign reading “DANGER—FEEDBACK” must be placed at each primary fuse to minimize the hazard of feedback voltage from one secondary winding to the other primary winding.
• Distribution transformer:
1. A distribution transformer has two high-voltage windings, rated at 2400 V each.
2. Small metal links are used to connect the two high-voltage windings either in series, for 4800-V primary service, or in parallel, for a 2400-V input. (Note that there are only two external high-voltage leads, which are marked with the standard designations H and H .)
3. The connections are made from the two windings at a terminal block slightly below the level of the insulating oil in the transformer case.
4. There are two secondary windings. These windings may be connected in parallel for 120-V service, or in series for 240-V service.
5. To obtain 120/240-V service, the two 120-V secondary windings are connected in series and a grounded neutral wire is connected between leads X2 and X3 .
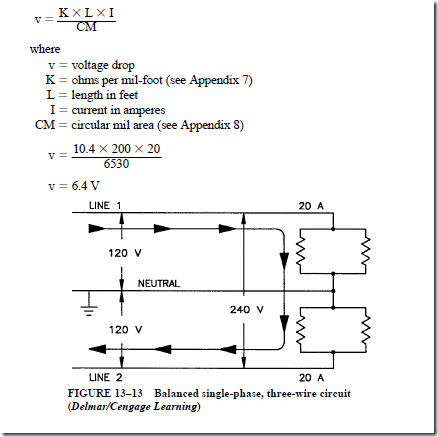
• Advantages of a single-phase, three-wire service:
1. This type of service provides two different voltages. The lower voltage supplies lighting and small appliance loads, and the higher voltage supplies heavy appliance and single-phase motor loads.
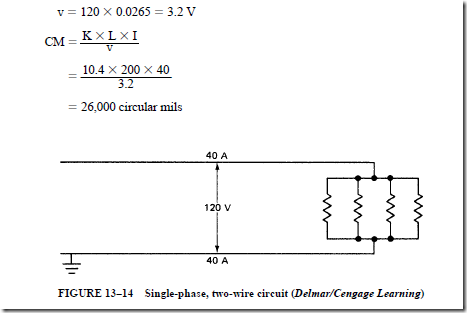
2. There are 240 V across the outside wires. Thus, the current for a given kilowatt load can be reduced by nearly half if the load is balanced between the neutral and the two outside wires.
a. Because of the reduction in the current, the voltage drop in the circuit conductors is reduced. Thus, the size of the conductor may be reduced and the voltage at the load is more nearly constant.
b. In addition, the following problems are minimized: dim lights, slow heating, and unsatisfactory appliance performance.
3. A single-phase, three-wire, 120/240-V system uses 37% less copper as compared to a 120-V, two-wire system having the same capacity and transmission efficiency.
• For the ac noninductive circuit, the current in the grounded neutral wire is the difference between the currents in the two outside legs.
1. For a balanced load on a three-wire, single-load service, the grounded neutral wire carries no current.
2. In a single-phase, three-wire circuit, the neutral wire is always grounded. The neutral wire is never fused or broken at any switch control point in the circuit.
3. With a direct path to ground by way of the neutral wire, any instantaneous high-voltage surge, such as that due to lightning, is instantly discharged to ground. In this way, the electrical equipment and the circuit wiring are protected from major lightning damage.
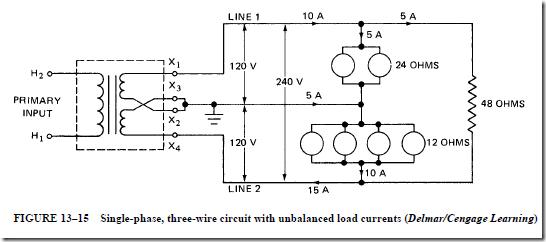
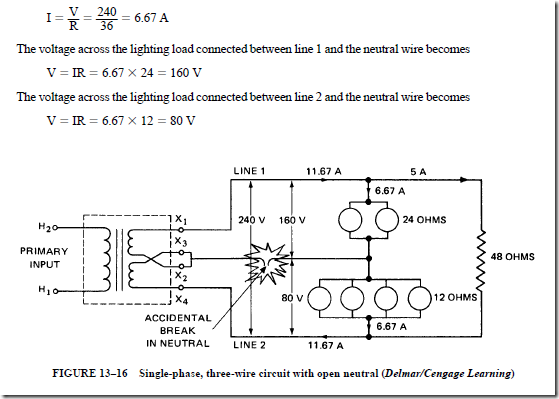
• Danger of an open neutral:
1. On a three-wire, single-phase system, the neutral wire helps maintain balanced voltages between each line wire and the neutral, even with unbalanced loads.
2. If the neutral wire is opened accidentally, there is an open circuit in the return path for the current from each device connected to the two outside wires back to the transformer.
3. Because of the open circuit, the devices are connected in series across the outside wires, or 240 V.
4. Some devices, such as lamps and motors, may have too great a voltage drop and will burn out. Other devices may receive a reduced voltage that does not permit proper operation of the load.
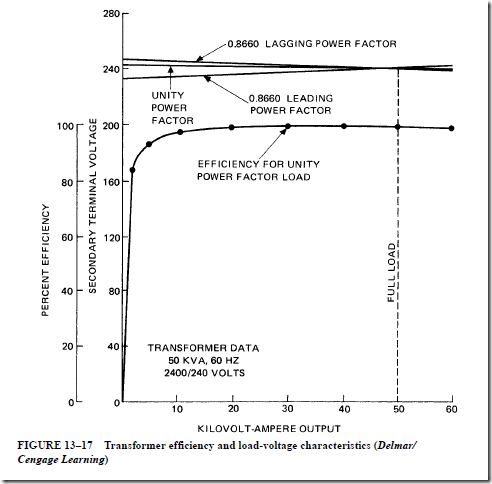
• A characteristic curve can be plotted showing the percent efficiency of a transformer.
1. The load–voltage characteristic curve usually shows that there is little change in the terminal voltage from a full-load condition to no-load condition on a trans- former whose efficiency is very high.
2. With a lagging power factor load, the secondary terminal voltage change is slightly greater than it is for a unity power factor load.
3. With a leading power factor load, the terminal voltage increases with the load, giving a negative voltage regulation.
• Cooling of transformers
1. The core-and-coil assembly is placed in a pressed steel tank and is completely covered with an insulating oil.
2. The insulating oil removes heat from the core and the coil windings. It also insu- lates the windings from the core and the transformer case.
3. The core-and-coil assembly contains channels or ducts to permit the circulation of the oil to remove the heat.
4. As the oil gains heat, its density decreases and it rises. As it rises, it contacts the tank walls and transfers the heat to the tank. The walls are cooled by air circula- tion. As the oil loses heat, its specific gravity increases and it returns to the bottom of the tank. This action is repeated over and over.
5. To obtain better cooling, the surface area of a transformer can be increased by adding tubes or fins to the steel tank assembly.
6. The insulating oil used in transformers is a high-grade oil that must be kept clean and moisture free.
7. Pyranol (manufactured by the General Electric Company) is a synthetic dielectric that is an effective, nonflammable, nonexplosive liquid cooling and insulating agent.
8. Other methods of cooling transformers include forced air circulation, natural air circulation, natural circulation of oil with water cooling, and forced oil circulation (for large transformers).
• Some voltage is lost in high-voltage distribution circuits.
1. The impressed voltage on the primary winding may be lower than indicated on the nameplate of the transformer.
2. As a result, the secondary terminal voltage is also lower than the nameplate value.
This condition is undesirable, and provisions can be made for changing taps to obtain the desired voltage.
3. The turns ratio of the transformer is adjusted by changing the taps.
a. The change in the tap connections can be made at the terminal board inside the transformer.
b. A tap-changing switch can be used to vary the number of turns of the primary winding, resulting in a change in the turns ratio.
c. A special tap switch, immersed in oil, may be used on some large transformers. This type of switch permits the tap connections to be changed under load. A small motor drives the tap-changing mechanism and is operated from a control panel.
• A transformer must be operated on an ac circuit at the frequency for which it is designed.
1. If a lower frequency is used, the reactance of the primary will decrease. The exciting current will increase, causing an increase in the flux density. The saturation of the core is above normal and there is a greater heat loss. Thus, the efficiency of the transformer is decreased.
2. If the frequency is greater than the nameplate value, the reactance will increase and the exciting current will decrease. There will be a lower flux density, but the core loss will remain nearly constant.
• A transformer must be operated at its rated primary voltage, as indicated on the nameplate.
1. If the voltage is increased to a high enough value above the nameplate rating, excessive heating will take place at the windings. The flux density of the core will increase, and saturation of the core will be above normal. Transformers are designed to operate without overheating at a voltage that is 5% above the rated voltage.
2. If the transformer is operated at a voltage lower than the nameplate rating, the power output will be reduced in proportion to the voltage decrease.
• Inrush current for a transformer can be very high compared to a choke.
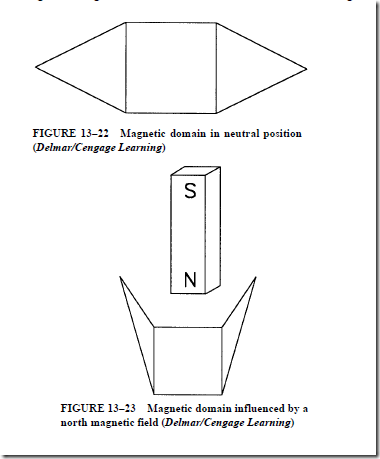
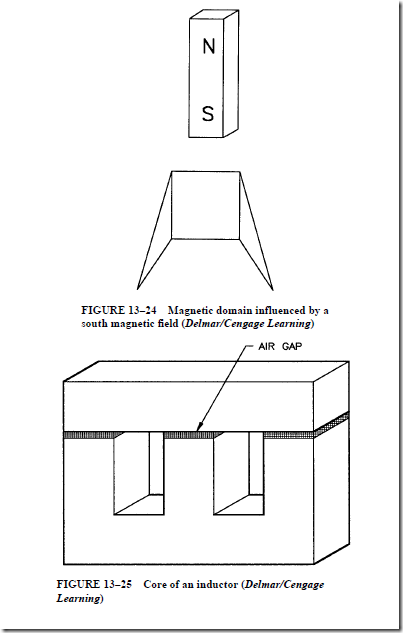
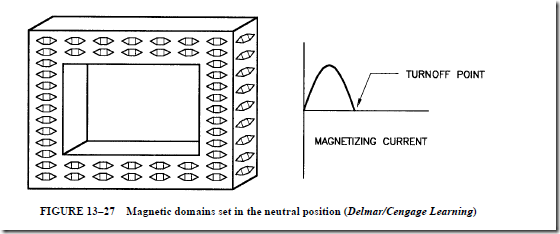
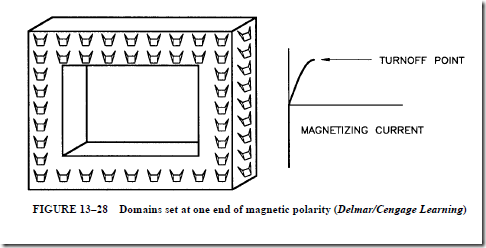
1. The magnetic domains in the core material of a transformer “remember” where they were set when the power is turned off.
2. Three factors that determine the amount of inrush current for a transformer are the amount of applied voltage, the resistance of the wire in the primary winding, and the flux change of the magnetic field in the core.
3. Magnetic domains or molecules can be made to reset to a neutral position by inserting an airgap in the core material.
• Transformer impedance is determined by the physical construction of the transformer.
1. Transformer impedance is expressed as a percent.
2. Transformer impedance is used to calculate the short-circuit current of a transformer.
Achievement Review
1. Define the term static transformer.
2. Explain what is meant by the terms primary and secondary, as applied to transformers.
|
3.
|
a.
b.
|
What is a stepdown transformer?
What is a stepup transformer?
|
|
4.
|
a.
b.
|
What is the relationship between the induced voltages on the primary and secondary windings and the number of turns of the two windings?
What is the difference between the impressed voltage and the induced voltage in the primary winding?
|
5. The primary winding of a transformer is rated at 115 V and the secondary winding is rated at 300 V. The primary winding has 500 turns. How many turns does the secondary winding have?
6. The transformer in question 5 has a full-load secondary output of 300 VA at 300 V.
a. What is the full-load secondary current?
b. Determine the full-load primary current (neglect all losses).
c. What is the relationship between the primary current and the secondary current and the number of turns on the two windings?
7. a. What is an exciting current?
b. What two functions does it perform?
8. a. Explain what is meant by core losses.
b. How can the core losses be kept to a minimum?
c. Draw a circuit diagram to show how the core loss, in watts, is measured for a 5-kVA transformer rated at 2400 to 240 V. The low-voltage side is used as the primary winding.
d. What safety precautions should be observed in measuring the core loss on the low-voltage side?
e. Using accurate instruments, should the core loss be the same for the high- voltage winding as for the primary?
9. The core loss of the transformer in question 8 is measured using the low-voltage side as the primary. The following data are obtained:
Voltmeter reading = 240 V
Exciting current = 1.0 A Wattmeter reading = 24 W
Determine
a. the core loss, in watts.
b. the power factor and the phase angle.
c. the in-phase component of the exciting current required for the core losses.
d. the lagging quadrature (magnetizing) component of the current.
10. Explain why the secondary ampere-turns oppose the magnetizing flux of the pri- mary winding.
11. List, in sequence, the reactions that take place in a transformer that result in an increase in the primary current input with an increase in the secondary current output to the load.
12. a. What is the primary leakage flux?
b. What is the secondary leakage flux?
c. What effect does leakage flux have on the operation of a transformer?
d. How can the leakage flux of a transformer be kept to a minimum?
13. Using diagrams, describe the three types of core construction used in transformers.
14. a. List the losses that occur in a transformer.
b. Which losses remain nearly constant at all load points? Why?
c. Which losses change when there is a change in the load? Why?
15. A 5-kVA, 240/120-V, 60-Hz transformer has a core loss of 32 W. The transformer has an effective resistance of 0.05 W in the high-voltage winding and 0.0125 W in the low-voltage winding. Determine the efficiency of the transformer at the rated load and unity power factor.
16. A 25-kVA, 2400/240-V, 60-Hz stepdown transformer has a core loss of 120 W. The effective resistance of the primary winding is 1.9 W. The effective resistance of the secondary winding is 0.02 W. Determine
a. the full-load current rating of the high-voltage and low-voltage windings. (Neglect any losses and assume that the input and the output are the same.)
b. the total copper losses of the transformer at the rated load.
c. the efficiency of the transformer at the rated load and a unity power factor.
17. Determine the efficiency of the transformer in question 15 at 50% of the rated load output and 0.l75 lagging power factor.
18. A 50-kVA, 4600/230-V, 60-Hz, single-phase, stepdown transformer is designed so that at the condition of full load and a unity power factor, the core losses equal the copper losses. The copper losses are equally divided between the two wind- ings. At full load the efficiency is 96.5%. Determine
a. the core losses.
b. the total copper losses.
c. the rated current of the primary and secondary windings. (Neglect the losses and assume that the input and the output are the same.)
d. the effective resistance of the primary and secondary windings.
19. Explain why it is hard to arrive at an accurate value of the efficiency of a trans- former using measurements of the power input and output.
20. a. Draw a diagram of the connections for the impedance short-circuit test for a single-phase transformer, rated at 20 kVA, 60 Hz, 4800/240 V. The high- voltage winding is the input side and is supplied from a 240-V ac source with a variable resistor in series.
b. Why should the measurements for the short-circuit test (part a) be made on the high-voltage side of the transformer?
21. The following data were obtained during the short-circuit test for the 20-kVA, 4800/240-V transformer in question 20:
Impedance voltage = 160 V
Ammeter reading = 4.2 A Wattmeter reading = 280 W
Another test shows the core loss to be 120 W. Determine
a. the efficiency at the rated load and a unity power factor.
b. the efficiency at 50% of the rated load and 0.80 lagging power factor.
22. a How are transformer leads marked?
b. Explain what is meant by additive polarity and subtractive polarity.
23. A transformer is used to step down a primary voltage of 4800 V to 240 V to sup- ply a single-phase load. Additional equipment is installed, making the kVA load greater than the full-load rating of the transformer. A second transformer, having the same kVA capacity, is to be operated in parallel with the first transformer.
a. List three requirements that are to be observed if the transformers are to share the load properly.
b. Explain the procedure used in connecting the second transformer in parallel.
24. a. There is a question about the accuracy of the turns ratio of a transformer rated at 2400/240 V. A 240-V test source is available in the laboratory. Assuming that voltmeters are available with the proper scales, explain how the voltage ratio can be determined. Draw a schematic diagram to clarify the answer.
b. Explain how the polarity of this transformer may be obtained using the 240-V test source.
25. A 30-kVA, 2400/240-V, 60-Hz transformer is used as a stepdown transformer.
The core loss is 150 W, the rated primary current is 12.5 A, the resistance of the primary winding is 1.5 W, the rated secondary current is 125 A, and the resistance of the secondary winding is 0.015 W. At the rated kVA capacity and a 0.75 lagging power factor, determine
a. the total copper losses.
b. the efficiency of the transformer.
26. A 20-kVA standard distribution transformer is rated at 2400/4800 V on the high- voltage side, and 120/240 V on the low-voltage side. The transformer has an efficiency of 97% when it is operating at the rated load as a stepdown transformer supplying a noninductive lighting load.
a. Draw a diagram to show the internal and external transformer connections required to step down the voltage from 2400 V to a 120/240-V, single- phase, three-wire service. Show the polarity markings for the transformer terminals for additive polarity.
b. What is the full-load secondary current if the load is balanced?
c. What is the power input to the primary side at the rated load?
d. If the no-load voltage of the 240-V secondary is 4 V more than the full- load voltage, what is the percentage voltage regulation?
27. Explain why the single-phase, 120/240-V, three-wire system is preferred to the single-phase, 120-V, two-wire system.
|
28.
|
a.
b.
|
Why is oil used in transformers?
What advantage is there in using Pyranol, instead of oil, in a transformer?
|
|
29.
|
a.
b.
|
Explain the process of cooling a transformer by the natural circulation of oil and air.
How can the heat-dissipating surface be increased for transformers with very large kVA ratings?
|
30. a. What is the purpose of a tap-changing switch as used on a transformer?
b. What are some of the applications of a transformer with tap-changing facilities?
31. Explain why a transformer has a high efficiency from 10% of the rated load to full load.
32. List the data commonly found on a transformer nameplate.
33. A 50-kVA single-phase transformer has a secondary voltage of 240 V. The name- plate indicates that the transformer has an impedance of 2.35%. What is the short- circuit current for this transformer?
34. A three-phase transformer is rated at 75 kVA and has a secondary voltage of 208
V. The nameplate indicates a transformer impedance of 3.5%. What is the short- circuit current for this transformer?
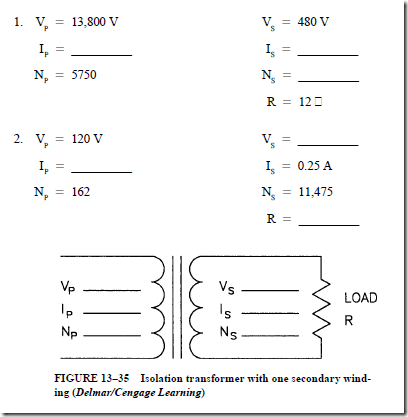
PRACTICE PROBLEMS FOR UNIT 13
Find the missing values in the following problems. Refer to Figure 13–35 and the formulas under the Transformers section of Appendix 15.

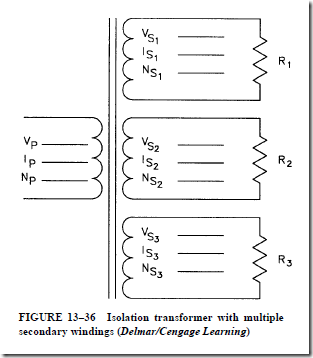
Find the missing values in the following problems. Refer to Figure 13–36 and the formulas listed under the Transformers section of Appendix 15.
[Note: Total primary current is equal to the sum of the primary currents needed to supply power to each secondary.]