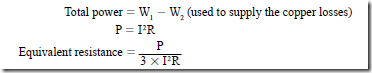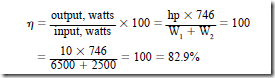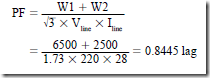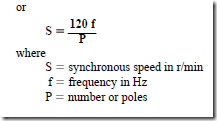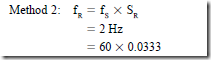science universe

COMPARISON BETWEEN SQUIRREL-CAGE AND WOUND-ROTOR INDUCTION MOTORS

The wound-rotor induction motor has the following advantages:

• High starting torque and low starting current if the motor is started with the maximum resistance inserted in the rotor circuit

• Variable speed

• Smooth acceleration under heavy loads

There are several disadvantages to this motor, including the following:

• Greater initial cost

• Higher maintenance and repair costs

• Low efficiency and poor speed regulation (when the motor is operated with resistance inserted in the rotor circuit)

SUMMARY

• A three-phase, squirrel-cage induction motor

1. is simple in construction and is easy to maintain.

2. is smaller in physical size than other motors for a given horsepower rating.

3. has very good speed regulation under varying load conditions.

4. is used for many industrial applications because of its low cost, rugged construction, and operating characteristics.

Other characteristics are as follows:

1. The basic components of a squirrel-cage motor are a stator, a rotor, and two end shields housing the bearings supporting the rotor shaft.

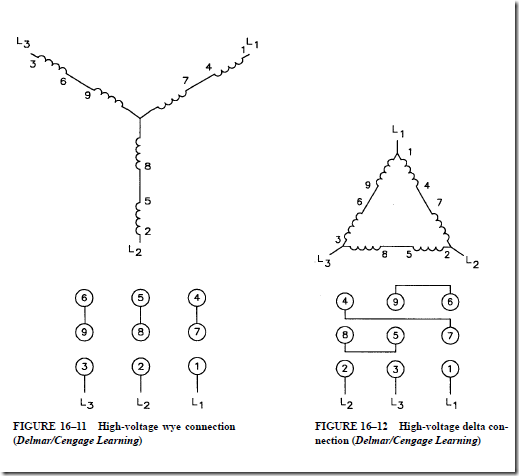
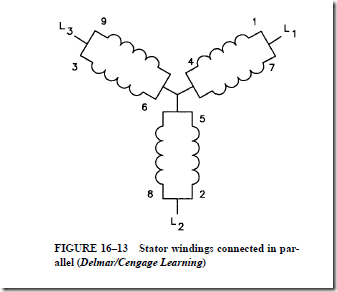
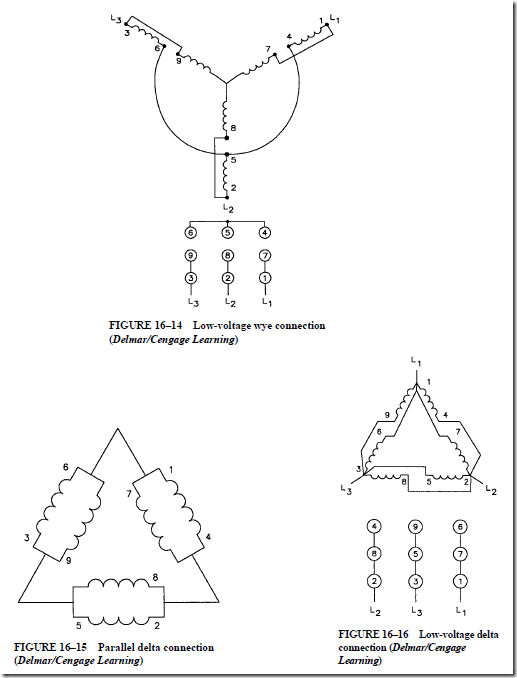
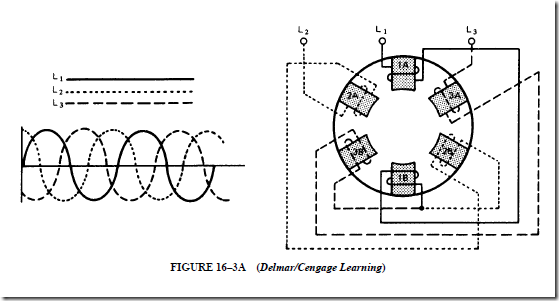
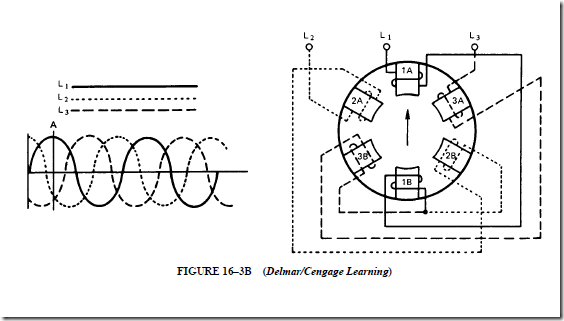
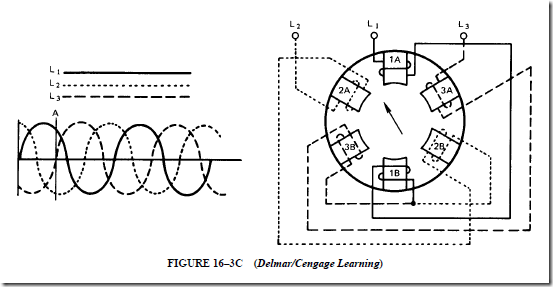
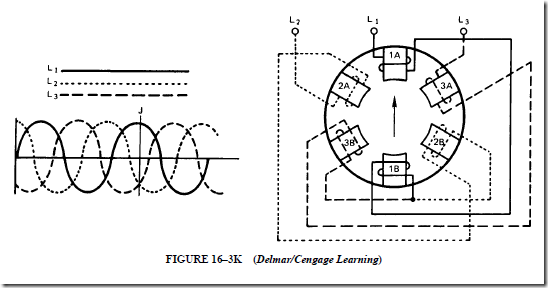
2. The stator is a three-phase winding that is placed in the slots of a laminated steel core. Three single-phase windings are spaced 120 electrical degrees apart. These windings may be connected in wye or delta.

3. The rotor consists of a cylindrical core made from steel laminations. Aluminum bars are mounted near the surface and are connected at the ends to two aluminum end rings.

• The squirrel-cage induction motor is also known as a synchronous speed motor.

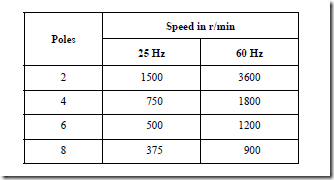
1. The synchronous speed is determined by the number of poles in the stator winding and the frequency of the ac source

where

S = synchronous speed, in r/min

f = frequency, in hertz

P = number of poles (not pairs of poles)

2. The following table lists the speeds of a motor at two different frequencies for different numbers of poles:

• Slip of an induction motor:

1. Slip is the difference between the synchronous speed of the motor and the actual speed of the rotor. The rotor always turns at a speed that is slightly less than synchronous speed.

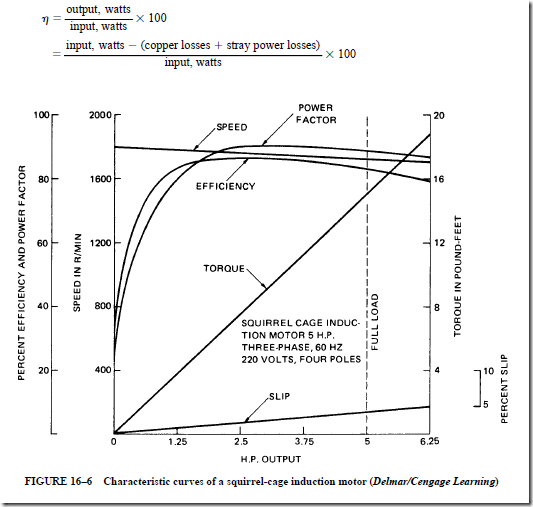
2. The speed performance of an induction motor is usually measured in terms of percent slip. The percent slip for an induction motor is generally in the range of 2% to 5%:

3. The standard squirrel-cage induction motor has excellent speed regulation, from no load to full load. Because of its good speed regulation, an induction motor is considered to be a constant-speed motor:

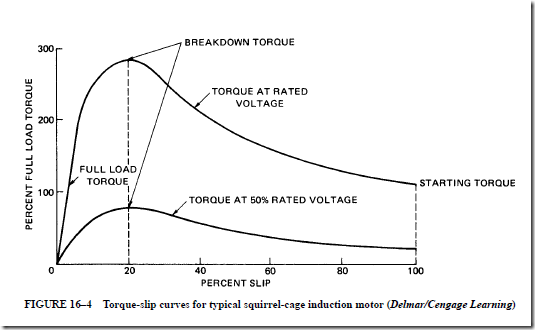
4. The torque output of an induction motor varies as the square of the terminal volt- age for a given percent slip.

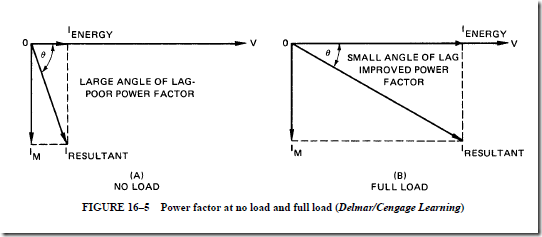
5. The power factor of the induction motor is low at no load and high at full load. At full-load conditions, the in-phase component of current is large and the magnetizing component is small; the opposite is true at no-load conditions.

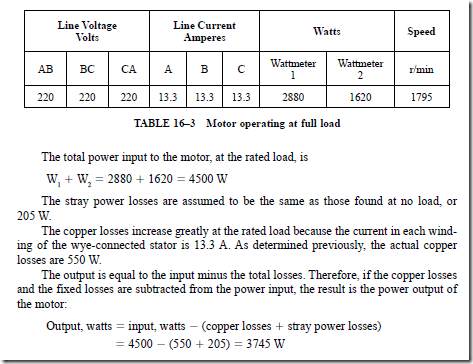
6. The losses of an induction motor consist of the stray power losses and the copper losses. The stray power losses are nearly constant at all loads. The copper losses increase as the current of the motor increases.

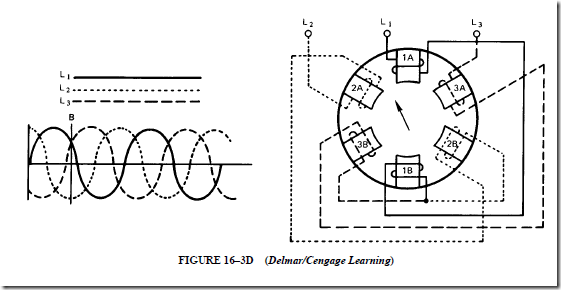
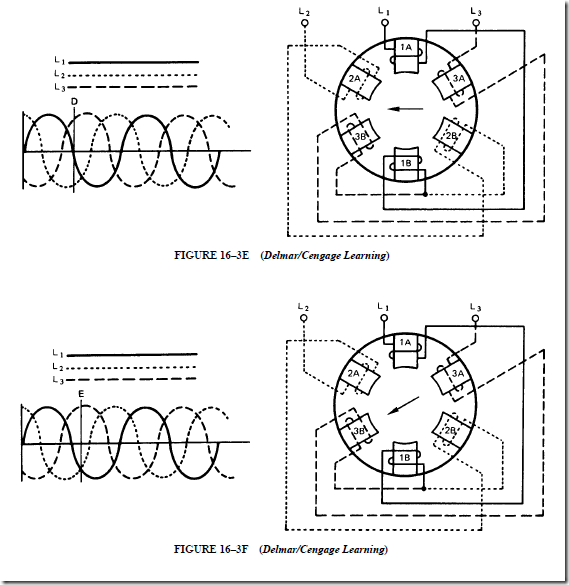
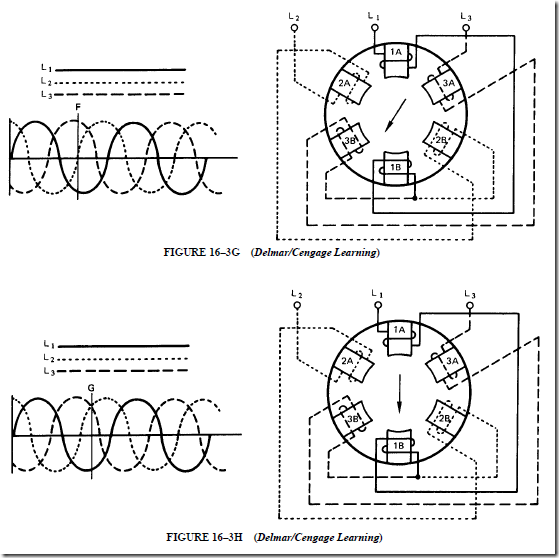
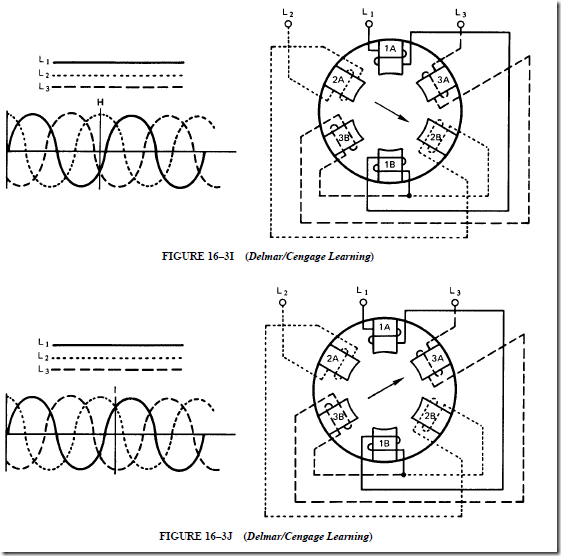
7. The direction of rotation of a three-phase, squirrel-cage induction motor can be changed by reversing two of the three incoming supply leads.

• The torque of an induction motor

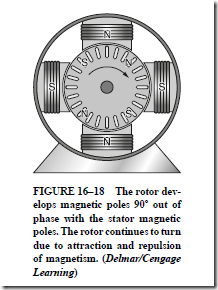
1. results from the interaction between the stator flux and the rotor flux.

2. is produced only when the rotor turns at a speed that is less than the synchronous speed of the stator flux pattern.

3. is small at no load because there is only a slight difference between the rotor speed and the synchronous speed of the stator flux.

4. will increase to a larger value as the load on the shaft of the rotor increases. The resulting increase in the rotor current causes a larger torque at a slightly lower rotor speed.

• Rotor frequency:

1. This frequency is an important factor in the operation of the motor. A change in the rotor frequency causes the inductive reactance and the impedance of the rotor to decrease. A change in the frequency will affect the starting and running characteristics of the motor.

2. Rotor frequency is expressed by the following formulas:

• At the instant of start-up

1. the rotor is not turning and there is 100% slip. The rotor frequency is equal to the stator frequency.

2. the inductive reactance of the rotor is very large compared to the effective resistance component. The rotor has a very low lagging power factor and the starting torque is low.

3. the stator field cuts the rotor bars at a faster rate; thus, the induced voltage in the rotor causes a large rotor current and the stator current will also be high at start-up.

In addition:

1. Because of the high starting current, induction motors must have starting protection. This protection may be rated as high as three times the full-load current rating of the motor.

2. Some very large induction motors are started with auxiliary starters. These devices reduce the motor voltage at start-up to limit the starting surge of current. As a result, there is less voltage disturbance on the feeder circuit supplying the motor load.

• The point of the maximum torque output is called the breakdown point.

1. An increase in the load beyond this point means that less torque is developed by the motor and the rotor stops.

2. The breakdown point occurs at 200% to 300% of the rated torque.

• The efficiency of an ac induction motor is given by the following equation:

• Brushes and slip rings are not required on a squirrel-cage induction motor. Thus, this type of motor can be used in locations where there is a possibility of explosion due to arcing, such as in chemical plants and flour or lumber mills.

• There is no practical method of providing stepless speed control for the induction motor.

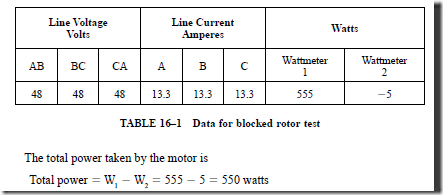
• The blocked rotor test is used to determine the equivalent resistance of the motor winding, per phase.

1. Two wattmeters are used in this test:

• Stray power losses:

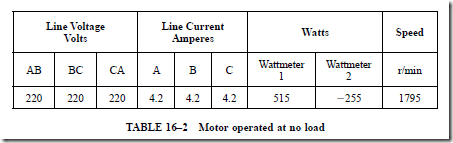
1. Stray power losses include mechanical friction losses, windage losses, and iron losses.

2. To measure these losses, the motor is operated at no load with the rated voltage applied to the motor terminals:

3. The fixed losses at no load are obtained by subtracting the no-load copper losses from the power input at no load:

• Speed control of an induction motor:

1. The synchronous speed of the magnetic field of the stator is determined by the number of stator poles and the frequency of the ac source.

2. Generally, the speed of an induction motor cannot be varied by changing the frequency.

3. The speed of a squirrel-cage motor may be changed if the motor is provided with special stator windings. When these windings are reconnected using special switch controls, different numbers of stator poles are formed. Thus, different speeds can be obtained for a squirrel-cage induction motor connected to an ac source at a fixed frequency.

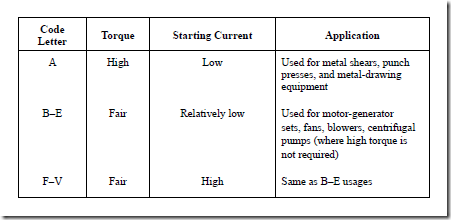
• Code letter identification for motors:

1. A system of code letters is used to identify certain induction motors. These motors are grouped according to their torque and starting current characteristics.

2. The code letter designates the ratio between the starting and full-load currents.

This letter appears on the nameplate of all squirrel-cage induction motors.

3. By referring to the National Electrical Code, this code letter can be used to deter- mine the current ratings of circuit breakers, fuses, and other overload protective devices.

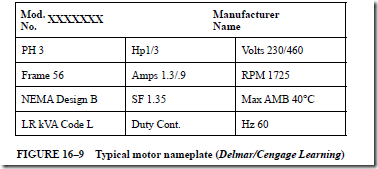
• A motor nameplate contains the following information:

Full-load horsepower output (hp)

Full-load speed (r/min)

Full-load current amperage (FLA)

Locked-rotor current amperage (LRA)

Manufacturer name

Terminal voltage (volts)

Number of phases (phase)

Frequency (cycles) (Hz)

Temperature rise (rise °C) (or insulation system class and rated ambient temperature)

Time rating (5, 15, 30, 60 min, or continuous)

Code letter

[Note: Other general information may be placed on the motor nameplate.]

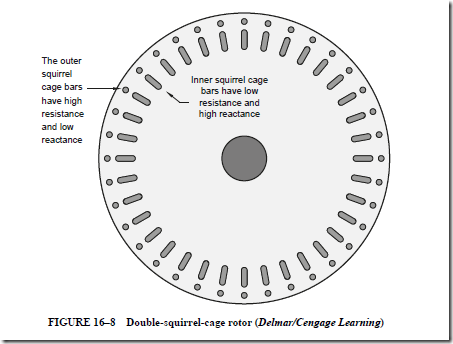
• A double-squirrel-cage motor has a low starting current, a strong starting torque, and excellent speed regulation. The starting torque for this type of motor can be as high as 250% of the rated torque.

• Single-phase operation of three-phase induction motors:

1. If a three-phase induction motor is running when it is subjected to single-phase conditions, it will continue to operate but at a greatly reduced capacity.

2. The motor will not have enough torque to start when it is energized from a single-phase source.

3. If the rated load is applied to the motor when it is operating as a single-phase motor, it will overheat and the insulation of the windings may be damaged.

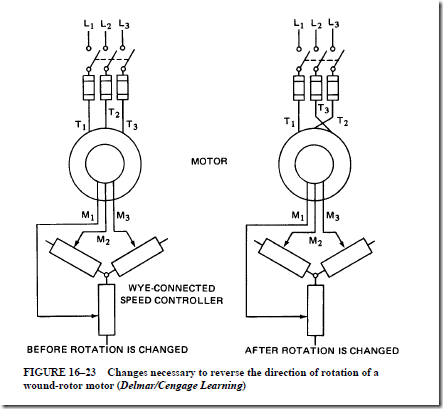
• The wound-rotor induction motor:

1. This motor can be used for variable-speed applications. The squirrel-cage induction motor is a constant-speed motor.

2. The formula used to find the synchronous speed for a squirrel-cage induction motor can also be used for the wound-rotor motor:

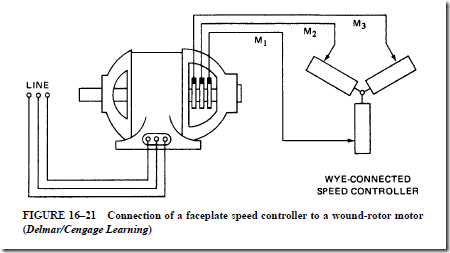
3. A wye-connected speed controller provides control current through slip rings to the windings of the rotor.

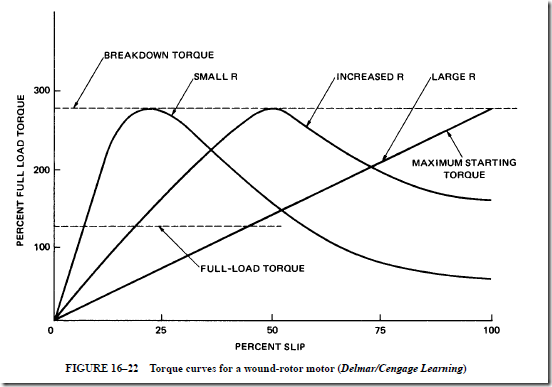
a. At start-up, all of the resistance of the wye-connected speed controller is inserted in the rotor circuit. This additional resistance causes an excellent starting torque and a large percent slip.

b. As the motor accelerates, steps of resistance are cut out of the wye-connected speed controller.

c. When all of the resistance is cut out, the rotor slip rings are short-circuited.

The motor then operates at the rated speed like a squirrel-cage induction motor.

d. This motor can be operated at heavy loads by cutting in resistance to the rotor circuit to obtain a below-normal speed at a lower motor efficiency.

4. The direction of rotation can be changed by reversing any two leads of the three line leads feeding to the stator windings.

5. A wound-rotor induction motor is used when a strong starting torque and a range of speed control are required. Typical applications include cranes, large compressors, elevators, and pumps.

6. Compared to the squirrel-cage induction motor, the wound-rotor motor has the following advantages:

a. High starting torque and low starting current if it is started with the maximum resistance inserted in the motor circuit

b. Variable speed

c. Smooth acceleration under heavy loads

7. Compared to the squirrel-cage induction motor, the wound-rotor motor has the following disadvantages:

a. Greater initial cost

b. Higher maintenance and repair costs

c. Low efficiency and poor speed regulation (when it is operated with resistance inserted in the rotor circuit)

Achievement Review

1. Explain what is meant by the synchronous speed of a three-phase induction motor.

2. What two conditions determine the synchronous speed of a three-phase induction motor?

3. Explain what is meant by the following terms:

 

	a. b. c.	Revolutions slip Percent slip Rotor frequency
4.	a. b.	What is the rotor frequency of a three-phase, 60-Hz, squirrel-cage induction motor at the instant of start? What is the approximate rotor frequency of a three-phase, 60-Hz, squirrel- cage induction motor when it is operating at the rated load?

5. What is the reason for the poor starting torque of a squirrel-cage induction motor?

6. A six-pole, three-phase, 60-Hz induction motor has a full-load speed of 1140 r/ min. Determine

a. the synchronous speed.

b. the revolutions slip.

c. the percent slip.

d. the rotor frequency.

7. a. Draw characteristic curves for a three-phase, squirrel-cage induction motor for the speed, percent slip, percent efficiency, power factor, and torque.

b. Discuss each of the five characteristic curves developed in part a of this question.

8. For a given value of slip, the torque output of an induction motor varies as the square of the impressed terminal voltage. Explain what is meant by this statement.

9. A 10-hp, 220-V, three-phase, 60-Hz, squirrel-cage induction motor is rated at 28 A per terminal. The full-load speed is 855 r/min, and the full-load power factor is 0.90 lag. The motor has eight poles. At the rated load, determine

a. the synchronous speed.

b. the slip in r/min.

c. the percent slip.

d. the rotor frequency at the rated speed.

10. A three-phase, 60-Hz, four-pole, 220-V, squirrel-cage induction motor takes 52 A per terminal at full load. The power factor is 0.85 lag, and the efficiency is 88%.

The slip is 3.0%. At the rated load, determine

a. the speed in r/min.

b. the horsepower output of the motor.

c. the total losses.

11. A three-phase, 60-Hz, six-pole, 220-V, squirrel-cage induction motor has a full- load output of 15 hp. The full-load efficiency is 87%, and the power factor is 0.88 lag. The windings of the motor are connected in delta. At the rated load, determine

a. the line current.

b. the phase winding voltage.

12. Assuming that the three-phase motor in question 11 is reconnected in wye with the same load and power factor, determine

a. the new rated line voltage.

b. the line current per motor terminal.

13. Explain how the direction of rotation is reversed for

a. a three-phase squirrel-cage induction motor.

b. a three-phase wound-rotor induction motor.

14. Explain why a three-phase squirrel-cage induction motor will not start when energized from a single-phase source.

15. Neither of the following alternating-current, three-phase induction motors is operating properly. Give a possible reason for the motor failure described, and state what should be done to correct each condition.

a. A 15-hp, 220 V, three-phase squirrel-cage induction motor overheats while operating at a normal load. The motor circuit is deenergized. When an attempt is made to restart the motor, it will not turn.

b. A 5-hp, 220-V, three-phase squirrel-cage induction motor stops as soon as the start push button for the across-the-line motor starter is released.

c. A newly installed 10-hp, 220-V, three-phase squirrel-cage induction motor has dual voltage ratings of 220 V and 440 V. The motor is supplied from a 220-V, three-phase source. At no load, the motor operates at a speed that is slightly below synchronous speed. When the rated load is applied, the motor stalls.

16. Show the connections for the nine terminal leads of a wye-connected, three-phase motor rated at 220/440 V for operation at

a. a line voltage of 440 V.

b. a line voltage of 220 V.

17. Compare a three-phase squirrel-cage induction motor and a three-phase wound-rotor induction motor, with regard to

a. construction.

b. starting torque.

c. speed control.

d. initial cost and maintenance.

e. efficiency.

18. a. Explain why the power factor of an induction motor is low at no load.

b. Explain what happens to the power factor as the load on an induction motor is increased.

19. Explain how both a good starting torque and small percent slip can be obtained using a squirrel-cage induction motor with a double-squirrel-cage rotor.

20. How is speed control provided for a squirrel-cage induction motor?

21. The following data are obtained in a prony brake test of a three-phase squirrel- cage induction motor:

Determine

a. the power factor.

b. the horsepower output.

c. the efficiency.

d. the torque output in pound • feet.

22. a. What are the losses in a squirrel-cage induction motor?

b. Which of these losses are constant and which of the losses vary with a change in load?

23. List the nameplate data of a typical squirrel-cage motor.

24. Code letters are included in the nameplate data for three-phase squirrel-cage induction motors. What is the purpose of these code letters?

25. What is the purpose of the protective starting device used on faceplate speed controllers and drum-type speed controllers?

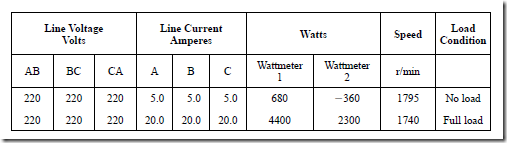
26. The following test data are obtained on a 7.5-hp, three-phase, 220-V, wye- connected, four-pole squirrel-cage induction motor. The data are for a no-load condition and a full-load condition. The effective resistance of each single-phase winding of the wye-connected stator is 0.65 11. Determine the stray power losses of the motor.

27. Use the data given in question 26 and determine

a. the copper losses of the motor at full load.

b. the efficiency of the motor at rated load.

c. the horsepower output at full load.

d. the torque output in pound • feet at full load.

28. A three-phase, squirrel-cage induction motor must carry an additional load. List the sequence of steps, in chronological order, showing how the motor will adjust itself to carry this additional load.

SINGLE-PHASE OPERATION OF THREE-PHASE INDUCTION MOTORS

A line wire feeds the stator windings of a three-phase induction motor. If this wire is opened, the motor will operate as a single-phase induction motor. It will not have enough torque to start when energized from a single-phase source. However, if the three-phase motor is running when the break in the line wire occurs, it will continue to operate with a greatly reduced capacity. If the rated load is applied to the motor when it is operating as a single-phase motor, it will overheat. The insulation of the windings may be damaged as a result.

The three-phase motor will not start on a single phase because the induced voltage and currents in the rotor set up a magnetic field in the rotor. This field opposes the stator field. (This situation is an application of Lenz’s law.) The rotor current produces a rotor field in which the rotor poles are centered with the stator field poles, as shown in Figure 16–18. As a result, there is no torque in either a clockwise or counterclockwise direction.

If the three-phase motor is operating at the rated speed when the single-phase condition develops, the rotor continues to turn. The moving rotor cuts the stator field flux and causes induced voltages and currents in the rotor bars. The rotor currents create a rotor field with poles midway between the stator poles. The rotor has high-reactance and low- resistance components. Therefore, the rotor current will lag behind the induced voltage in the rotor by nearly 90%. As a result, the rotor and stator fields are practically 90% out of phase with each other. The rotor current produces magnetic polarities that are 90º out-of- phase with those produced in the stator. The motor continues to operate due to attraction and repulsion of magnetism in the same manner as a single-phase induction motor. The three-phase motor will continue to run, but at reduced capacity. Once the motor has been stopped, it cannot restart because a rotating magnetic field cannot be produced with a single phase.

THE WOUND-ROTOR INDUCTION MOTOR

Many industrial applications require three-phase motors with variable-speed control. The basic squirrel-cage induction motor is a constant speed motor. Thus, another type of induction motor is required for variable-speed applications. The wound-rotor induction motor meets these needs.

The wound-rotor induction motor has nearly the same stator construction and winding arrangement as the squirrel-cage induction motor. Figure 16–19 shows a typical stator for a wound-rotor induction motor.

A wound rotor is shown in Figure 16–20. The cylindrical core of the rotor is made up of steel laminations. Slots are cut into the cylindrical core to hold the formed coils for three single-phase windings. These windings are placed 120 electrical degrees apart. The insulated coils of the rotor winding are grouped to form the same number of poles as in the stator windings. The three single-phase rotor windings are connected in wye.

Three leads from these windings terminate at three slip rings mounted on the rotor shaft. Carbon brushes ride on these slip rings and are held securely by adjustable springs mounted in the brush holders. The brush holders are fixed rigidly, because it is not necessary to vary their position. Leads from the carbon brushes are connected to an external speed controller.

Principle of Operation

When the stator windings of a wound-rotor motor are energized from a three-phase source, the rotating magnetic field formed travels around the inside of the stator core, just as in a squirrel-cage induction motor. The speed of the rotating magnetic field depends on the number of stator poles and the frequency of the source. The formula used to find the synchronous speed for squirrel-cage induction motors can also be used for this type of motor:

As the rotating field travels at the synchronous speed, it cuts the wound-rotor windings and induces voltages in these windings. The induced voltages set up currents that form a closed-circuit path from the rotor windings through the slip rings and brushes to a wye-connected speed controller. Figure 16–21 shows a wound-rotor induction motor connected to a wye-connected speed controller.

Speed Control

At start-up, all of the resistance of the wye-connected speed controller is inserted in the rotor circuit. This additional resistance causes an excellent starting torque and a large percent slip. The added resistance in the rotor circuit increases the impedance. Because the rotor circuit has a large resistance component and a small reactive component, the rotor current is nearly in phase with the stator field flux. Thus, there is a maximum interaction between the two fields, resulting in a strong starting torque.

As the motor accelerates, steps of resistance are cut out of the wye-connected speed controller. When all of the resistance is cut out, the rotor slip rings are short-circuited. The motor then operates at the rated speed like a squirrel-cage induction motor. The speed of the wound-rotor motor can be changed by inserting or removing resistance in the rotor circuit using a wye-connected speed controller.

This motor can be operated at heavy loads by cutting in resistance to the rotor circuit to obtain a below-normal speed. However, the I2 R losses in the rotor circuit are high and cause a large reduction in the motor efficiency. Additional resistance inserted in the rotor circuit leads to poor speed regulation. This effect is due to the large increase in slip that is necessary to obtain the required torque increase with an increase in the load.

Torque Performance

The curves in Figure 16–22 show the torque performance of a wound-rotor induc- tion motor. When the proper value of resistance is inserted in the rotor circuit, the starting torque has its maximum value at 100% slip (at start-up). If all of the resistance is cut out of the speed controller, and the motor is started, the starting torque is poor.

In this case, the rotor circuit has a large reactive component and a small resistance component. This means that the motor will have the same starting torque characteristic as a squirrel-cage induction motor.

REVERSE ROTATION

The direction of rotation of a wound-rotor induction motor can be reversed. To do this, interchange the connections of any two of the three line leads feeding to the stator wind- ings. Note that both the wound-rotor and the squirrel-cage induction motors are reversed using the same procedure. Reversing the phase sequence of the three-phase input to the stator windings changes the direction of rotation of the magnetic field produced by these windings. Therefore, the direction of rotation of the rotor is reversed. Figure 16–23 shows the connection changes that are required to reverse the direction of rotation. There is no reversal in the direction of rotation of the motor when any of the leads feeding from the slip rings of the speed controller are interchanged.

TERMINAL MARKINGS

The stator leads of a three-phase, wound-rotor induction motor are marked T , T , and T . This is the same marking system used with three-phase, squirrel-cage induction motors.

The rotor leads are marked M , M , and M . The M lead connects to the rotor ring nearest the bearing housing. The M lead connects to the middle slip ring, and the M lead connects to the slip ring nearest the rotor windings.

OPERATING CHARACTERISTICS

The wound-rotor motor and the squirrel-cage motor have the same percent efficiency, power factor, percent slip, speed, and torque characteristics. This statement is true if the wound-rotor motor is operated from no load to full load with all of the resistance cut out of the rotor circuit. If the motor is operated at or near the rated load while there is resistance in the rotor circuit, there will be I2 R losses in the resistance components of the speed controller. These losses cause a decrease in the motor efficiency. When the motor is operated with resistance in the rotor circuit, there is also a sharp increase in percent slip with an increase in the load. The percent slip must increase to obtain the required increase in the rotor current so that there is a larger value of torque to meet the increased load demands.

If the motor is started with all of the resistance of the speed controller inserted in the rotor circuit, the starting torque will be at a maximum with 100% slip. The starting surge of current to the stator is limited to a relatively low value. The current is low because of the high resistance inserted in the rotor.

The wound-rotor induction motor is used when a strong starting torque and a range of speed control are required. Typical applications for this motor include cranes, large compressors, elevators, and pumps. This type of motor is also used in the heavy-steel industry for applications requiring adjustable speed.

SINGLE-PHASE OPERATION OF THREE-PHASE INDUCTION MOTORS

A line wire feeds the stator windings of a three-phase induction motor. If this wire is opened, the motor will operate as a single-phase induction motor. It will not have enough torque to start when energized from a single-phase source. However, if the three-phase motor is running when the break in the line wire occurs, it will continue to operate with a greatly reduced capacity. If the rated load is applied to the motor when it is operating as a single-phase motor, it will overheat. The insulation of the windings may be damaged as a result.

The three-phase motor will not start on a single phase because the induced voltage and currents in the rotor set up a magnetic field in the rotor. This field opposes the stator field. (This situation is an application of Lenz’s law.) The rotor current produces a rotor field in which the rotor poles are centered with the stator field poles, as shown in Figure 16–18. As a result, there is no torque in either a clockwise or counterclockwise direction.

If the three-phase motor is operating at the rated speed when the single-phase condition develops, the rotor continues to turn. The moving rotor cuts the stator field flux and causes induced voltages and currents in the rotor bars. The rotor currents create a rotor field with poles midway between the stator poles. The rotor has high-reactance and low- resistance components. Therefore, the rotor current will lag behind the induced voltage in the rotor by nearly 90%. As a result, the rotor and stator fields are practically 90% out of phase with each other. The rotor current produces magnetic polarities that are 90º out-of- phase with those produced in the stator. The motor continues to operate due to attraction and repulsion of magnetism in the same manner as a single-phase induction motor. The three-phase motor will continue to run, but at reduced capacity. Once the motor has been stopped, it cannot restart because a rotating magnetic field cannot be produced with a single phase.

THE WOUND-ROTOR INDUCTION MOTOR

Many industrial applications require three-phase motors with variable-speed control. The basic squirrel-cage induction motor is a constant speed motor. Thus, another type of induction motor is required for variable-speed applications. The wound-rotor induction motor meets these needs.

The wound-rotor induction motor has nearly the same stator construction and winding arrangement as the squirrel-cage induction motor. Figure 16–19 shows a typical stator for a wound-rotor induction motor.

A wound rotor is shown in Figure 16–20. The cylindrical core of the rotor is made up of steel laminations. Slots are cut into the cylindrical core to hold the formed coils for three single-phase windings. These windings are placed 120 electrical degrees apart. The insulated coils of the rotor winding are grouped to form the same number of poles as in the stator windings. The three single-phase rotor windings are connected in wye.

Three leads from these windings terminate at three slip rings mounted on the rotor shaft. Carbon brushes ride on these slip rings and are held securely by adjustable springs mounted in the brush holders. The brush holders are fixed rigidly, because it is not necessary to vary their position. Leads from the carbon brushes are connected to an external speed controller.

Principle of Operation

When the stator windings of a wound-rotor motor are energized from a three-phase source, the rotating magnetic field formed travels around the inside of the stator core, just as in a squirrel-cage induction motor. The speed of the rotating magnetic field depends on the number of stator poles and the frequency of the source. The formula used to find the synchronous speed for squirrel-cage induction motors can also be used for this type of motor:

As the rotating field travels at the synchronous speed, it cuts the wound-rotor windings and induces voltages in these windings. The induced voltages set up currents that form a closed-circuit path from the rotor windings through the slip rings and brushes to a wye-connected speed controller. Figure 16–21 shows a wound-rotor induction motor connected to a wye-connected speed controller.

Speed Control

At start-up, all of the resistance of the wye-connected speed controller is inserted in the rotor circuit. This additional resistance causes an excellent starting torque and a large percent slip. The added resistance in the rotor circuit increases the impedance. Because the rotor circuit has a large resistance component and a small reactive component, the rotor current is nearly in phase with the stator field flux. Thus, there is a maximum interaction between the two fields, resulting in a strong starting torque.

As the motor accelerates, steps of resistance are cut out of the wye-connected speed controller. When all of the resistance is cut out, the rotor slip rings are short-circuited. The motor then operates at the rated speed like a squirrel-cage induction motor. The speed of the wound-rotor motor can be changed by inserting or removing resistance in the rotor circuit using a wye-connected speed controller.

This motor can be operated at heavy loads by cutting in resistance to the rotor circuit to obtain a below-normal speed. However, the I2 R losses in the rotor circuit are high and cause a large reduction in the motor efficiency. Additional resistance inserted in the rotor circuit leads to poor speed regulation. This effect is due to the large increase in slip that is necessary to obtain the required torque increase with an increase in the load.

Torque Performance

The curves in Figure 16–22 show the torque performance of a wound-rotor induc- tion motor. When the proper value of resistance is inserted in the rotor circuit, the starting torque has its maximum value at 100% slip (at start-up). If all of the resistance is cut out of the speed controller, and the motor is started, the starting torque is poor.

In this case, the rotor circuit has a large reactive component and a small resistance component. This means that the motor will have the same starting torque characteristic as a squirrel-cage induction motor.

REVERSE ROTATION

The direction of rotation of a wound-rotor induction motor can be reversed. To do this, interchange the connections of any two of the three line leads feeding to the stator wind- ings. Note that both the wound-rotor and the squirrel-cage induction motors are reversed using the same procedure. Reversing the phase sequence of the three-phase input to the stator windings changes the direction of rotation of the magnetic field produced by these windings. Therefore, the direction of rotation of the rotor is reversed. Figure 16–23 shows the connection changes that are required to reverse the direction of rotation. There is no reversal in the direction of rotation of the motor when any of the leads feeding from the slip rings of the speed controller are interchanged.

TERMINAL MARKINGS

The stator leads of a three-phase, wound-rotor induction motor are marked T , T , and T . This is the same marking system used with three-phase, squirrel-cage induction motors.

The rotor leads are marked M , M , and M . The M lead connects to the rotor ring nearest the bearing housing. The M lead connects to the middle slip ring, and the M lead connects to the slip ring nearest the rotor windings.

OPERATING CHARACTERISTICS

The wound-rotor motor and the squirrel-cage motor have the same percent efficiency, power factor, percent slip, speed, and torque characteristics. This statement is true if the wound-rotor motor is operated from no load to full load with all of the resistance cut out of the rotor circuit. If the motor is operated at or near the rated load while there is resistance in the rotor circuit, there will be I2 R losses in the resistance components of the speed controller. These losses cause a decrease in the motor efficiency. When the motor is operated with resistance in the rotor circuit, there is also a sharp increase in percent slip with an increase in the load. The percent slip must increase to obtain the required increase in the rotor current so that there is a larger value of torque to meet the increased load demands.

If the motor is started with all of the resistance of the speed controller inserted in the rotor circuit, the starting torque will be at a maximum with 100% slip. The starting surge of current to the stator is limited to a relatively low value. The current is low because of the high resistance inserted in the rotor.

The wound-rotor induction motor is used when a strong starting torque and a range of speed control are required. Typical applications for this motor include cranes, large compressors, elevators, and pumps. This type of motor is also used in the heavy-steel industry for applications requiring adjustable speed.

PROCEDURE FOR MEASURING MOTOR LOSSES

On many occasions, it is necessary to measure the losses of a squirrel-cage induction motor to determine the motor output and efficiency. The two types of losses for this motor are the copper losses and the fixed losses. The output of the motor is equal to the input of the motor minus the losses.

For example, assume that a test is made of a three-phase, squirrel-cage induction motor. The motor is rated at 5 hp, 220 V, 13.3 A, 1735 r/min, and 60 Hz. The motor has four poles and is wye-connected.

Equivalent Resistance

The first step is to obtain the equivalent resistance of the motor windings. The three-phase power and current input to the motor are measured with the rotor stationary. A very low value of three-phase voltage, at the rated frequency, is applied to the test circuit. This voltage is increased until the rated current is indicated by the three ammeters. This test is called the blocked rotor test. The data from this test are given in Table 16–1.

Note that the rated current of 13.3 A is achieved at only 48 V, three phase. The core losses are negligible at this low voltage. Therefore, it is assumed that the total power input of 550 W is used to supply the copper losses.

It is now possible to find the “equivalent ac resistance” per phase for the three wye- connected windings. The power loss in one phase winding is I2 R. For the three windings, the power loss is P = 3 I² R, where W is the power taken by the blocked rotor motor and R is the equivalent resistance per phase:

It is simple to calculate the copper losses for any load current knowing the effective resistance of each single-phase winding.

Stray Power Losses

The stray power losses include mechanical friction losses, windage losses, and iron losses. To measure these losses, the motor is operated at no load with the rated voltage applied to the motor terminals. The data shown in Table 16–2 are the result of this part of the test.

The following procedure is used to determine the fixed losses or the stray power losses. Total power input at no load:

The stray power losses can be measured at no load only. It is assumed that these losses remain nearly constant from no load to full load. This assumption can be made because the speed of a squirrel-cage motor remains almost constant from no load to full load. Also, the magnetizing current is nearly constant throughout the load range of the motor.

Total Losses, Output, and Efficiency

The motor can now be loaded to any desired load point to determine the total losses, the output, and the efficiency. The data obtained with the motor operating at full load are given in Table 16–3.

The discussion on motor losses does not include a detailed study of the variations of certain factors that were assumed to be constants. A more complete study of motor losses can be obtained by consulting electrical engineering texts.

SPEED CONTROL

The synchronous speed of the magnetic field of the stator is determined by the number of stator poles and the frequency of the ac source. Generally, it is not possible to vary the speed of an induction motor by changing its frequency. (Nearly all motors are operated from an ac source having a fixed frequency.) In a few applications, a single alternator may supply one or two motors. In these cases, the frequency can be changed by varying the speed of the prime mover. As a result, the motor speed changes.

Squirrel-cage motors may be provided with special stator windings. When these windings are reconnected by special switch controls, different numbers of stator poles are formed. In this way, different speeds are obtained from a squirrel-cage induction motor connected to an ac source having a fixed frequency.

One type of multispeed squirrel-cage motor is designed for two synchronous speeds, where one speed is twice the other. This two-speed motor has one stator winding. A switch control device is used with this winding to provide two synchronous speeds. For example, speeds of 900 r/min and 1800 r/min may be obtained, or 1800 r/min and 3600 r/min.

CODE LETTER IDENTIFICATION

Squirrel-cage rotors are not all the same. Rotors are made with different types of bars. The type of rotor bars used in the construction of the rotor determines the operating characteristics of the motor. AC squirrel-cage motors are given a code letter on their nameplate. These code letters should not be confused with the NEMA code letter found on motors manufactured since 1999. The code letter indicates the type of bars used in the rotor. Figure 16–7A shows a rotor with type A bars. A type A rotor has the highest resistance of any squirrel-cage rotor. This means that the starting torque will be high per ampere of starting current because the rotor current is closer to being in phase with the induced voltage than any other type of rotor. Also, the high resistance of the rotor bars limits the amount of current flow in the rotor when starting. This produces a low starting current for the motor. A rotor with type A bars has very poor running characteristics, however. Because the bars are resistive, a large amount of voltage will have to be induced into the rotor to produce an increase in rotor current and, therefore, an increase in the rotor magnetic field. This means that when load is added to the motor, the rotor must slow down a great amount to produce enough cur- rent in the rotor to increase the torque. Motors with type A rotors have the highest per- cent slip of any squirrel-cage motor. Motors with type A rotors are generally used in applications where starting is a problem, such as a motor that must accelerate a large flywheel from 0 r/min to its full speed. Flywheels can have a very large amount of inertia, which may require several minutes to accelerate them to their running speed when they are stated.

Figure 16–7B shows a rotor with bars similar to those found in rotors with code letters B through E. These rotor bars have lower resistance than the type A rotor. Rotors of this type have fair starting torque, low starting current, and fair speed regulation.

Figure 16–7C shows a rotor with bars similar to those found in rotors with code letters F through V. This rotor has low starting torque per ampere of starting cur- rent. The starting current is high, and these motors exhibit good running torque. Motors containing rotors of this type generally have very good speed regulation and low percent slip. It should be noted that although motors with rotors that fall into this range exhibit poor starting torque per ampere of starting current, the starting torque is still greater than the amount of running torque. These motors do not generally exhibit difficulty starting unless the load requires some time to reach normal speed. The extended time will cause the high starting current to overheat the windings.

The Double-Squirrel-Cage Rotor

Some motors use a rotor that contains two sets of squirrel-cage windings (Figure 16–8). The outer winding consists of bars with a relatively high resistance located close to the top of the iron core. Because these bars are located close to the surface, they have a relatively low reactance. The inner winding consists of bars with a large cross-sectional area that gives them a low resistance. The inner winding is placed deeper in the core material, which causes it to have a much higher reactance.

This type of rotor has a high starting torque per ampere of starting current, and low starting current. It is constructed with small rotor bars located near the surface of the rotor. It is used in motors that power metal shears, punch presses, and metal drawing equipment.

This type of rotor exhibits high reactance and low resistance. Motors with rotors of this type have relatively low starting current and fair starting torque per ampere of starting current. They are generally used for motor generator sets, blowers, centrifugal pumps, and other applications that do not require high starting torque.

FIGURE 16–7 Various types of squirrel-cage rotors (Delmar/Cengage Learning)

When the double-squirrel-cage motor is started, the rotor frequency is high. Because the inner winding is inductive, its impedance will be high as compared to the resistance of the outer winding. During this period of time, most of the rotor current flows through the outer winding. The resistance of the outer winding limits the cur- rent flow through the rotor, which limits the starting current to a relatively low value. Because the current is close to being in phase with the induced voltage, the rotor flux and stator flux are close to being in phase with each other, and a strong starting torque is developed. The starting torque of a double-squirrel-cage motor can be as high as 250% of rated full-load torque.

When the rotor reaches its full-load speed, rotor frequency decreases to 2 or 3 Hz. The inductive reactance of the inner winding has now decreased to a low value. Most of the rotor current now flows through the low-resistance inner winding. This type motor has good running torque and excellent speed regulation.

MOTOR NAMEPLATE DATA

The data contained on the typical nameplate for a squirrel-cage induction motor include the following items: horsepower rating, full-load speed, full-load amperes, volt- age, number of phases, frequency, frame number, permissible temperature rise, model number, manufacturer name, locked-rotor ampere code letter, service factor, and NEMA code letter. The NEMA code letter should not be confused with the code letter for locked- rotor amperes. The NEMA code letter is used to determine the fuse or circuit breaker

size for the motor circuit. The locked-rotor amperes code letter describes the type of bars in the rotor and is used in conjunction with NEC® Section 430 to determine the starting current of the motor. A typical nameplate for a squirrel-cage induction motor is shown in Figure 16–9.

STATOR WINDING CONNECTIONS

Many of the three-phase motors used in industry are designed to be operated on two voltages, such as 240 or 480 V. Motors of this type contain two sets of windings per phase. Most dual voltage motors bring out nine T leads at the terminal box. There

is a standard method used to number these leads, as shown in Figure 16–10. Starting with terminal 1, the leads are numbered in a decreasing spiral. Another method of determining the proper lead numbers is to add three to each terminal. For example, starting with lead 1, add three to one. Three plus one equals four. The phase winding that begins with 1 ends with 4. Now add three to four. Three plus four equals seven. The beginning of the second winding for phase one is seven. This method will work for the windings of all phases. If in doubt, draw a diagram of the phase windings and number them in a spiral.

Three-phase motors can be constructed to operate in either wye or delta. If a motor is to be connected to high voltage, the phase windings will be connected in series. In Figure 16–11, a schematic diagram and terminal connection chart for high voltage are

 

shown for a wye-connected motor. In Figure 16–12, a schematic diagram and terminal connection chart for high voltage are shown for a delta-connected motor.

When a motor is to be connected for low-voltage operation, the phase windings must be connected in parallel. Figure 16–13 shows the basic schematic diagram for a wye-connected motor with parallel phase windings. In actual practice, however, it is not possible to make this exact connection with a nine-lead motor. The schematic shows that terminal 4 connects to the other end of the phase windings that starts with terminal 7. Terminal 5 connects to the other end of winding 8, and terminal 6 connects to the other end of winding 9. In actual motor construction, the opposite ends of windings 7, 8, and 9 are connected together inside the motor and are not brought outside the motor case. The problem is solved, however, by forming a second wye connection by connecting terminals 4, 5, and 6 together, as shown in Figure 16–14.

The phase winding of a delta-connected motor must also be connected in parallel for use on low voltage. A schematic for this connection is shown in Figure 16–15. A connection diagram and terminal connection for this hookup is shown in Figure 16–16.

Some dual-voltage motors will contain twelve T leads instead of nine. In this instance, the opposite ends of terminals 7, 8, and 9 are brought out for connection. Figure 16–17 shows the standard numbering for both delta- and wye-connected motors. Twelve leads are brought out if the motor is intended to be used for wye–delta starting. When this is the case, the motor must be designed for normal operation with its windings connected in delta. If the windings are connected in wye during starting, the starting current of the motor is greatly reduced.

PROCEDURE FOR MEASURING MOTOR LOSSES

On many occasions, it is necessary to measure the losses of a squirrel-cage induction motor to determine the motor output and efficiency. The two types of losses for this motor are the copper losses and the fixed losses. The output of the motor is equal to the input of the motor minus the losses.

For example, assume that a test is made of a three-phase, squirrel-cage induction motor. The motor is rated at 5 hp, 220 V, 13.3 A, 1735 r/min, and 60 Hz. The motor has four poles and is wye-connected.

Equivalent Resistance

The first step is to obtain the equivalent resistance of the motor windings. The three-phase power and current input to the motor are measured with the rotor stationary. A very low value of three-phase voltage, at the rated frequency, is applied to the test circuit. This voltage is increased until the rated current is indicated by the three ammeters. This test is called the blocked rotor test. The data from this test are given in Table 16–1.

Note that the rated current of 13.3 A is achieved at only 48 V, three phase. The core losses are negligible at this low voltage. Therefore, it is assumed that the total power input of 550 W is used to supply the copper losses.

It is now possible to find the “equivalent ac resistance” per phase for the three wye- connected windings. The power loss in one phase winding is I2 R. For the three windings, the power loss is P = 3 I² R, where W is the power taken by the blocked rotor motor and R is the equivalent resistance per phase:

It is simple to calculate the copper losses for any load current knowing the effective resistance of each single-phase winding.

Stray Power Losses

The stray power losses include mechanical friction losses, windage losses, and iron losses. To measure these losses, the motor is operated at no load with the rated voltage applied to the motor terminals. The data shown in Table 16–2 are the result of this part of the test.

The following procedure is used to determine the fixed losses or the stray power losses. Total power input at no load:

The stray power losses can be measured at no load only. It is assumed that these losses remain nearly constant from no load to full load. This assumption can be made because the speed of a squirrel-cage motor remains almost constant from no load to full load. Also, the magnetizing current is nearly constant throughout the load range of the motor.

Total Losses, Output, and Efficiency

The motor can now be loaded to any desired load point to determine the total losses, the output, and the efficiency. The data obtained with the motor operating at full load are given in Table 16–3.

The discussion on motor losses does not include a detailed study of the variations of certain factors that were assumed to be constants. A more complete study of motor losses can be obtained by consulting electrical engineering texts.

SPEED CONTROL

The synchronous speed of the magnetic field of the stator is determined by the number of stator poles and the frequency of the ac source. Generally, it is not possible to vary the speed of an induction motor by changing its frequency. (Nearly all motors are operated from an ac source having a fixed frequency.) In a few applications, a single alternator may supply one or two motors. In these cases, the frequency can be changed by varying the speed of the prime mover. As a result, the motor speed changes.

Squirrel-cage motors may be provided with special stator windings. When these windings are reconnected by special switch controls, different numbers of stator poles are formed. In this way, different speeds are obtained from a squirrel-cage induction motor connected to an ac source having a fixed frequency.

One type of multispeed squirrel-cage motor is designed for two synchronous speeds, where one speed is twice the other. This two-speed motor has one stator winding. A switch control device is used with this winding to provide two synchronous speeds. For example, speeds of 900 r/min and 1800 r/min may be obtained, or 1800 r/min and 3600 r/min.

CODE LETTER IDENTIFICATION

Squirrel-cage rotors are not all the same. Rotors are made with different types of bars. The type of rotor bars used in the construction of the rotor determines the operating characteristics of the motor. AC squirrel-cage motors are given a code letter on their nameplate. These code letters should not be confused with the NEMA code letter found on motors manufactured since 1999. The code letter indicates the type of bars used in the rotor. Figure 16–7A shows a rotor with type A bars. A type A rotor has the highest resistance of any squirrel-cage rotor. This means that the starting torque will be high per ampere of starting current because the rotor current is closer to being in phase with the induced voltage than any other type of rotor. Also, the high resistance of the rotor bars limits the amount of current flow in the rotor when starting. This produces a low starting current for the motor. A rotor with type A bars has very poor running characteristics, however. Because the bars are resistive, a large amount of voltage will have to be induced into the rotor to produce an increase in rotor current and, therefore, an increase in the rotor magnetic field. This means that when load is added to the motor, the rotor must slow down a great amount to produce enough cur- rent in the rotor to increase the torque. Motors with type A rotors have the highest per- cent slip of any squirrel-cage motor. Motors with type A rotors are generally used in applications where starting is a problem, such as a motor that must accelerate a large flywheel from 0 r/min to its full speed. Flywheels can have a very large amount of inertia, which may require several minutes to accelerate them to their running speed when they are stated.

Figure 16–7B shows a rotor with bars similar to those found in rotors with code letters B through E. These rotor bars have lower resistance than the type A rotor. Rotors of this type have fair starting torque, low starting current, and fair speed regulation.

Figure 16–7C shows a rotor with bars similar to those found in rotors with code letters F through V. This rotor has low starting torque per ampere of starting cur- rent. The starting current is high, and these motors exhibit good running torque. Motors containing rotors of this type generally have very good speed regulation and low percent slip. It should be noted that although motors with rotors that fall into this range exhibit poor starting torque per ampere of starting current, the starting torque is still greater than the amount of running torque. These motors do not generally exhibit difficulty starting unless the load requires some time to reach normal speed. The extended time will cause the high starting current to overheat the windings.

The Double-Squirrel-Cage Rotor

Some motors use a rotor that contains two sets of squirrel-cage windings (Figure 16–8). The outer winding consists of bars with a relatively high resistance located close to the top of the iron core. Because these bars are located close to the surface, they have a relatively low reactance. The inner winding consists of bars with a large cross-sectional area that gives them a low resistance. The inner winding is placed deeper in the core material, which causes it to have a much higher reactance.

This type of rotor has a high starting torque per ampere of starting current, and low starting current. It is constructed with small rotor bars located near the surface of the rotor. It is used in motors that power metal shears, punch presses, and metal drawing equipment.

This type of rotor exhibits high reactance and low resistance. Motors with rotors of this type have relatively low starting current and fair starting torque per ampere of starting current. They are generally used for motor generator sets, blowers, centrifugal pumps, and other applications that do not require high starting torque.

FIGURE 16–7 Various types of squirrel-cage rotors (Delmar/Cengage Learning)

When the double-squirrel-cage motor is started, the rotor frequency is high. Because the inner winding is inductive, its impedance will be high as compared to the resistance of the outer winding. During this period of time, most of the rotor current flows through the outer winding. The resistance of the outer winding limits the cur- rent flow through the rotor, which limits the starting current to a relatively low value. Because the current is close to being in phase with the induced voltage, the rotor flux and stator flux are close to being in phase with each other, and a strong starting torque is developed. The starting torque of a double-squirrel-cage motor can be as high as 250% of rated full-load torque.

When the rotor reaches its full-load speed, rotor frequency decreases to 2 or 3 Hz. The inductive reactance of the inner winding has now decreased to a low value. Most of the rotor current now flows through the low-resistance inner winding. This type motor has good running torque and excellent speed regulation.

MOTOR NAMEPLATE DATA

The data contained on the typical nameplate for a squirrel-cage induction motor include the following items: horsepower rating, full-load speed, full-load amperes, volt- age, number of phases, frequency, frame number, permissible temperature rise, model number, manufacturer name, locked-rotor ampere code letter, service factor, and NEMA code letter. The NEMA code letter should not be confused with the code letter for locked- rotor amperes. The NEMA code letter is used to determine the fuse or circuit breaker

size for the motor circuit. The locked-rotor amperes code letter describes the type of bars in the rotor and is used in conjunction with NEC® Section 430 to determine the starting current of the motor. A typical nameplate for a squirrel-cage induction motor is shown in Figure 16–9.

STATOR WINDING CONNECTIONS

Many of the three-phase motors used in industry are designed to be operated on two voltages, such as 240 or 480 V. Motors of this type contain two sets of windings per phase. Most dual voltage motors bring out nine T leads at the terminal box. There

is a standard method used to number these leads, as shown in Figure 16–10. Starting with terminal 1, the leads are numbered in a decreasing spiral. Another method of determining the proper lead numbers is to add three to each terminal. For example, starting with lead 1, add three to one. Three plus one equals four. The phase winding that begins with 1 ends with 4. Now add three to four. Three plus four equals seven. The beginning of the second winding for phase one is seven. This method will work for the windings of all phases. If in doubt, draw a diagram of the phase windings and number them in a spiral.

Three-phase motors can be constructed to operate in either wye or delta. If a motor is to be connected to high voltage, the phase windings will be connected in series. In Figure 16–11, a schematic diagram and terminal connection chart for high voltage are

 

shown for a wye-connected motor. In Figure 16–12, a schematic diagram and terminal connection chart for high voltage are shown for a delta-connected motor.

When a motor is to be connected for low-voltage operation, the phase windings must be connected in parallel. Figure 16–13 shows the basic schematic diagram for a wye-connected motor with parallel phase windings. In actual practice, however, it is not possible to make this exact connection with a nine-lead motor. The schematic shows that terminal 4 connects to the other end of the phase windings that starts with terminal 7. Terminal 5 connects to the other end of winding 8, and terminal 6 connects to the other end of winding 9. In actual motor construction, the opposite ends of windings 7, 8, and 9 are connected together inside the motor and are not brought outside the motor case. The problem is solved, however, by forming a second wye connection by connecting terminals 4, 5, and 6 together, as shown in Figure 16–14.

The phase winding of a delta-connected motor must also be connected in parallel for use on low voltage. A schematic for this connection is shown in Figure 16–15. A connection diagram and terminal connection for this hookup is shown in Figure 16–16.

Some dual-voltage motors will contain twelve T leads instead of nine. In this instance, the opposite ends of terminals 7, 8, and 9 are brought out for connection. Figure 16–17 shows the standard numbering for both delta- and wye-connected motors. Twelve leads are brought out if the motor is intended to be used for wye–delta starting. When this is the case, the motor must be designed for normal operation with its windings connected in delta. If the windings are connected in wye during starting, the starting current of the motor is greatly reduced.

POWER FACTOR

A squirrel-cage induction motor operating at no load has a low power factor in the range of 10% to 15% lag. The current input to an induction motor at no load consists of a large component of quadrature magnetizing current and a very small component of in-phase current to supply the losses. The resulting power factor angle between the coil voltage and the coil current for each phase winding is large (Figure 16–5A).

As the load on the motor increases, the in-phase current supplied to the motor increases. At the same time, there is little change in the magnetizing component. The resultant current is more nearly in phase with the voltage, as shown in Figure 16–5B. A smaller angle of lag results in a higher power factor. At the rated load, the power factor may be as high as 85% to 90% lagging.

SUMMARY OF OPERATING CHARACTERISTICS

The three-phase, squirrel-cage induction motor operates at a relatively constant speed from no load to full load. The rotor has a very low impedance. As a result, only a slight decrease in speed will cause a large increase in the rotor current. This current develops the necessary torque to turn the increased load. The percent slip at no load is less than 1%. At full load, the percent slip is usually between 3% and 5%. A squirrel-cage induction motor is considered to be a constant-speed motor because of this small change in percent slip from no load to full load. The slip increases as a straight-line characteristic, as shown in Figure 16–6. The rotor current will likewise increase in practically a direct proportion. Thus, the torque increases as a straight-line characteristic.

Figure 16–6 shows the characteristic curves of a 5-hp, three-phase, 220-V, 60-Hz, four- pole, squirrel-cage induction motor. The speed, percent slip, torque, efficiency, and power factor curves are included in this figure.

Induction Motor Losses

The losses in an induction motor consist of the stray power losses and the copper losses. The stray power losses include mechanical friction losses, windage losses, and iron losses. These losses are nearly constant at all load points and are often called fixed losses.

The copper losses consist of the I2 R losses in the windings of the motor. An increase in the load causes the current to increase in the motor windings. As a result, the I2 R losses increase. At light loads, the percent efficiency is low because the fixed losses are a large part of the input. As the load on the motor increases, the losses become a smaller part of the input. Thus, the efficiency increases to its maximum value. However, when the rated capacity of the motor is exceeded, the copper losses become excessive and the efficiency decreases.

The efficiency of an ac induction motor is given by the following equation:

Power Factor of Induction Motor

The power factor curve in Figure 16–6 shows a value at no load of approximately 0.15 lag. The no-load current consists mainly of magnetizing current. This current produces the mmf required to send the stator flux across the airgap and through the magnetic circuit. The in-phase component of the no-load current is low because the losses are small. Therefore, the no-load current lags the voltage by a large phase angle and the power factor is low. As the load on the motor increases, the in-phase current component supplied to the motor increases, the phase angle decreases, and the power factor increases. In practice, the power factor of the inductive motor at the rated load is between 0.85 and 0.90 lag.

Advantages of Induction Motor

The squirrel-cage induction motor has several advantages:

• It has excellent speed regulation with a small percent slip. This means that it is ideal for constant-speed applications.

• The motor is simple in construction and requires little maintenance or repairs.

• Brushes and slip rings are not required. Thus, it can be used in locations such as chemical plants and flour and lumber mills where there is the possibility of explosions due to arcing.

The major disadvantagse of the squirrel-cage induction motor is that there is no practical method of providing stepless speed control. Thus, this motor cannot be used in applications where variable speeds are required.

PROBLEM 2

Statement of the Problem

A test is made on a squirrel-cage induction motor when it delivers the rated load out- put. The motor is delta-connected and is a 10-hp, three-phase machine. The two-wattmeter method is used to obtain the following values:

Solution

1. The percent efficiency is the ratio of the output in watts to the input in watts. The rated nameplate output is 10 hp. This value must be expressed in watts. The total input to the motor is the sum of the two wattmeter readings:

2. The power factor is the ratio of the true power to the apparent power. This ratio is expressed by the following formula. This formula can be used for both delta- and wye-connected three-phase loads:

Statement of the Problem

A three-phase, 220-V, 60-Hz, six-pole, squirrel-cage induction motor takes 13.4 A per terminal at the rated load. The power factor is 0.88 lag. The efficiency is 83%. The percent slip at the rated load is 4%.

1. What is the full-load speed?

2. What is the rotor frequency?

3. What is the horsepower output at the rated load?

4. Determine the torque in pound • feet at the rated load and the rated speed.

Solution

1. The synchronous speed of this motor is

3. The horsepower output at the rated load can be determined once the true power input to the motor is known. The percent efficiency given in the problem is used to deter- mine the output in watts. This value is then converted to horsepower:

The prony brake method is not commonly used to determine the horsepower output of electric motors. However, the formula can be simplified and transposed to give the torque output of a motor at a given load point if the speed in r/min is known. The transposed formula used to find torque in pound • feet is

PROBLEM 4

Statement of the Problem

A three-phase induction motor is connected to a 480-V, 60-Hz power source. An ammeter indicates a current of 54 amperes supplying the motor. A three-phase wattmeter indicates a true power of 29 kW for the motor.

1. Determine the power factor of the motor.

2. Determine the amount of capacitance necessary to correct the power factor to 95%.

It is to be assumed that the capacitors will be connected in parallel with the motor and the capacitors will be wye-connected.

3. Determine the amount of current the circuit should draw after the power factor has been corrected to 95%.

Solution

1. Determine the power factor of the motor.

Determine the apparent power:

2. Determine the capacitance necessary to correct the power factor to 95%.

To determine the amount of capacitance needed, it is first necessary to determine the apparent power at a power factor of 95%.

To determine the amount of capacitance necessary to correct the power factor, sub- tract the present apparent power from the desired apparent power. This will indicate the capacitive VARs necessary to correct the power factor to 95%.

Determine the amount of capacitive reactance necessary to produce a current of 36.8 amperes. Because the capacitors form the phases of a wye connection, the voltage across

the capacitors will be the phase value of the wye connection, which is less than the line voltage by a factor of 3, or 277 volts.

POWER FACTOR

A squirrel-cage induction motor operating at no load has a low power factor in the range of 10% to 15% lag. The current input to an induction motor at no load consists of a large component of quadrature magnetizing current and a very small component of in-phase current to supply the losses. The resulting power factor angle between the coil voltage and the coil current for each phase winding is large (Figure 16–5A).

As the load on the motor increases, the in-phase current supplied to the motor increases. At the same time, there is little change in the magnetizing component. The resultant current is more nearly in phase with the voltage, as shown in Figure 16–5B. A smaller angle of lag results in a higher power factor. At the rated load, the power factor may be as high as 85% to 90% lagging.

SUMMARY OF OPERATING CHARACTERISTICS

The three-phase, squirrel-cage induction motor operates at a relatively constant speed from no load to full load. The rotor has a very low impedance. As a result, only a slight decrease in speed will cause a large increase in the rotor current. This current develops the necessary torque to turn the increased load. The percent slip at no load is less than 1%. At full load, the percent slip is usually between 3% and 5%. A squirrel-cage induction motor is considered to be a constant-speed motor because of this small change in percent slip from no load to full load. The slip increases as a straight-line characteristic, as shown in Figure 16–6. The rotor current will likewise increase in practically a direct proportion. Thus, the torque increases as a straight-line characteristic.

Figure 16–6 shows the characteristic curves of a 5-hp, three-phase, 220-V, 60-Hz, four- pole, squirrel-cage induction motor. The speed, percent slip, torque, efficiency, and power factor curves are included in this figure.

Induction Motor Losses

The losses in an induction motor consist of the stray power losses and the copper losses. The stray power losses include mechanical friction losses, windage losses, and iron losses. These losses are nearly constant at all load points and are often called fixed losses.

The copper losses consist of the I2 R losses in the windings of the motor. An increase in the load causes the current to increase in the motor windings. As a result, the I2 R losses increase. At light loads, the percent efficiency is low because the fixed losses are a large part of the input. As the load on the motor increases, the losses become a smaller part of the input. Thus, the efficiency increases to its maximum value. However, when the rated capacity of the motor is exceeded, the copper losses become excessive and the efficiency decreases.

The efficiency of an ac induction motor is given by the following equation:

Power Factor of Induction Motor

The power factor curve in Figure 16–6 shows a value at no load of approximately 0.15 lag. The no-load current consists mainly of magnetizing current. This current produces the mmf required to send the stator flux across the airgap and through the magnetic circuit. The in-phase component of the no-load current is low because the losses are small. Therefore, the no-load current lags the voltage by a large phase angle and the power factor is low. As the load on the motor increases, the in-phase current component supplied to the motor increases, the phase angle decreases, and the power factor increases. In practice, the power factor of the inductive motor at the rated load is between 0.85 and 0.90 lag.

Advantages of Induction Motor

The squirrel-cage induction motor has several advantages:

• It has excellent speed regulation with a small percent slip. This means that it is ideal for constant-speed applications.

• The motor is simple in construction and requires little maintenance or repairs.

• Brushes and slip rings are not required. Thus, it can be used in locations such as chemical plants and flour and lumber mills where there is the possibility of explosions due to arcing.

The major disadvantagse of the squirrel-cage induction motor is that there is no practical method of providing stepless speed control. Thus, this motor cannot be used in applications where variable speeds are required.

PROBLEM 2

Statement of the Problem

A test is made on a squirrel-cage induction motor when it delivers the rated load out- put. The motor is delta-connected and is a 10-hp, three-phase machine. The two-wattmeter method is used to obtain the following values:

Solution

1. The percent efficiency is the ratio of the output in watts to the input in watts. The rated nameplate output is 10 hp. This value must be expressed in watts. The total input to the motor is the sum of the two wattmeter readings:

2. The power factor is the ratio of the true power to the apparent power. This ratio is expressed by the following formula. This formula can be used for both delta- and wye-connected three-phase loads:

Statement of the Problem

A three-phase, 220-V, 60-Hz, six-pole, squirrel-cage induction motor takes 13.4 A per terminal at the rated load. The power factor is 0.88 lag. The efficiency is 83%. The percent slip at the rated load is 4%.

1. What is the full-load speed?

2. What is the rotor frequency?

3. What is the horsepower output at the rated load?

4. Determine the torque in pound • feet at the rated load and the rated speed.

Solution

1. The synchronous speed of this motor is

3. The horsepower output at the rated load can be determined once the true power input to the motor is known. The percent efficiency given in the problem is used to deter- mine the output in watts. This value is then converted to horsepower:

The prony brake method is not commonly used to determine the horsepower output of electric motors. However, the formula can be simplified and transposed to give the torque output of a motor at a given load point if the speed in r/min is known. The transposed formula used to find torque in pound • feet is

PROBLEM 4

Statement of the Problem

A three-phase induction motor is connected to a 480-V, 60-Hz power source. An ammeter indicates a current of 54 amperes supplying the motor. A three-phase wattmeter indicates a true power of 29 kW for the motor.

1. Determine the power factor of the motor.

2. Determine the amount of capacitance necessary to correct the power factor to 95%.

It is to be assumed that the capacitors will be connected in parallel with the motor and the capacitors will be wye-connected.

3. Determine the amount of current the circuit should draw after the power factor has been corrected to 95%.

Solution

1. Determine the power factor of the motor.

Determine the apparent power:

2. Determine the capacitance necessary to correct the power factor to 95%.

To determine the amount of capacitance needed, it is first necessary to determine the apparent power at a power factor of 95%.

To determine the amount of capacitance necessary to correct the power factor, sub- tract the present apparent power from the desired apparent power. This will indicate the capacitive VARs necessary to correct the power factor to 95%.

Determine the amount of capacitive reactance necessary to produce a current of 36.8 amperes. Because the capacitors form the phases of a wye connection, the voltage across

the capacitors will be the phase value of the wye connection, which is less than the line voltage by a factor of 3, or 277 volts.

SYNCHRONOUS SPEED

The speed at which the magnetic field rotates is known as the synchronous speed. The synchronous speed of a three-phase motor is determined by two factors:

1. The number of stator poles

2. The frequency of the ac line

Because 60 Hz is a standard frequency throughout the United States and Canada, the following gives the synchronous speeds for motors with different numbers of poles:

Speed Performance

The field set up by the stator windings cuts the copper bars of the rotor. Voltages induced in the squirrel-cage winding set up currents in the rotor bars. As a result, a field is created on the rotor core. The attraction between the stator field and the rotor field causes the rotor to follow the stator field. The rotor always turns at a speed that is slightly less than that of the stator field (less than the synchronous speed). In this way, the stator field cuts the rotor bars and induces the necessary rotor voltages and currents to create the rotor field.

The torque produced by an induction motor results from the interaction between the stator flux and the rotor flux. If the rotor is turned at the same speed as the stator field, there will be no relative motion between the rotor bars and the stator field. This means that no torque can be produced. A torque is produced only when the rotor turns at a speed that is less than synchronous speed. At no load, the mechanical losses of the motor can be over- come by a small torque. The rotor speed will be slightly less than the synchronous speed of the stator field.

As a mechanical load is applied to the motor shaft, the rotor speed will decrease. The stator field turns at a constant synchronous speed and cuts the rotor bars at a faster rate per second. The voltages and currents induced in the rotor bars increase accordingly, causing a greater induced rotor voltage. The resulting increase in the rotor current causes a large torque at a slightly lower speed.

The squirrel-cage winding was described as consisting of heavy copper bars welded to two end rings. The impedance of this winding is relatively low. Therefore, a slight decrease in the speed causes a large increase in the currents in the rotor bars. Because the rotor circuit of a squirrel-cage induction motor has a low impedance, the speed regulation of this motor is very good.

PERCENT SLIP

The speed performance of squirrel-cage induction motors is measured in terms of percent slip. In determining percent slip, the synchronous speed of the stator field is used as a reference point. The synchronous speed for a particular motor is constant, because the number of poles and the frequency remain the same. Slip is the number of revolutions per minute by which the rotor falls behind the speed of the rotating field of the stator. Slip is determined by subtracting the speed of the rotor from the synchronous speed of the stator field. For example, a three-phase, two-pole induction motor has a full-load speed of 3480 r/min. The synchronous speed of the stator field is

Smaller values of percent slip mean that the motor has better speed regulation. When determined at the rated load, the percent slip of most squirrel-cage induction motors varies from 2% to 5%. This type of motor is considered to be a constant-speed motor because there is a small decrease in the speed between the no-load and full-load points.

ROTOR FREQUENCY

In the previous example, the rotor slips behind the speed of the stator field by 120 revolutions per minute. The flux of the two stator poles passes a given rotor bar of the squirrel-cage winding only 120 times every minute. Thus, the voltages and currents induced in the rotor will have a very low frequency. The rotor frequency is

Unit 1 showed that when a conductor passes a pair of unlike poles, one cycle (Hz) of voltage is induced in the conductor. In this example, a pair of stator poles passes a given bar in the squirrel-cage rotor 120 times per minute or twice per second. Thus, the frequency must be 2 Hz. If the slip is increased, the rotor frequency will increase, because the flux of the revolving field will cut a given bar in the squirrel-cage winding more times per second. This relationship can be expressed as a formula

Note that methods 1 and 2 both give the same frequency for the rotor. This frequency is an important factor in the operation of the motor. A change in the rotor frequency causes a change in the inductive reactance component (X= 2Tif L) of the rotor impedance. Thus, a change in the frequency will affect the starting and running characteristics of the motor.

PROBLEM 1

Statement of the Problem

A 5-hp, 220-V, three-phase, 60-Hz, squirrel-cage induction motor has eight poles. At the rated load, it has a speed of 870 r/min. Determine

1. the synchronous speed.

2. the percent slip, at the rated load.

3. the rotor frequency, at the instant of start-up.

4. ssthe rotor frequency, at the rated load.

Solution

1. The synchronous speed of the stator field is found using the frequency formula trans- posed to solve for S:

2. At the rated load, the percent slip is

3. At start-up, the rotor is not turning. The slip at this instant is unity, or 100%. There- fore, the rotor frequency and the stator frequency are both 60 Hz.

4. The rotor turns at 870 r/min at the rated load. The rotor frequency at this speed can be determined as follows:

Method 1:

Slip, in r/min = synchronous speed – rotor speed

= 900 – 870 = 30 r/min

TORQUE AND SPEED CHARACTERISTICS

The torque produced by an induction motor depends on the strengths of the stator and rotor fields and the phase relationship between the fields:

This torque formula is similar to the formula for the torque of a dc motor: T = k X 8f X IA. The difference between the formulas is in the cos 8R function. The equivalent dia- gram of the rotor is an inductor and resistor in series. Because rotor frequency is a function of slip, it follows that cos 8R varies with slip.

STARTING CHARACTERISTICS

At the instant the motor is started, the rotor is not turning and there is 100% slip. The rotor frequency at this moment is equal to the stator frequency. The inductive reactance of the rotor is very large compared to the effective resistance component. Also, the rotor has a very low lagging power factor. This means that the rotor flux lags the stator flux by a large phase angle. As a result, the interaction between the two fields is small and the starting torque is low.

As the speed of the motor increases, the percent slip and the frequency of the rotor decrease. The decrease in the rotor frequency causes the inductive reactance and the impedance of the rotor to decrease. Thus, the phase angle between the stator and rotor fluxes is reduced. The torque then increases to its maximum value at about 20% slip. As the rotor continues to accelerate, the torque decreases until it reaches the value required to turn the mechanical load applied to the motor shaft. The slip at this point is between 2% and 5%.

Starting Current

At start-up the stator field cuts the rotor bars at a faster rate than when the rotor is turning. The large voltage induced in the rotor causes a large rotor current. As a result, the stator current will also be high at start-up. The squirrel-cage induction motor resembles a static transformer during this brief instant. That is, the stator may be viewed as the primary or input winding, and the squirrel-cage rotor winding as the secondary winding.

Most three-phase, squirrel-cage induction motors are started with the rated line voltage applied directly to the motor terminals. This means that the starting surge of current reaches a value as high as three to five times the full-load current rating of the motor. This high starting current requires induction motors to have starting protection. This protection may be rated as high as three times the full-load current rating of the motor. In some instances, very large induction motors are started with auxiliary starters. These devices reduce the motor voltage at start-up to limit the starting surge of current. As a result, there is less voltage disturbance on the feeder circuit supplying the motor load.

Starting with Reduced Voltage

There are problems in starting a large induction motor with a reduced voltage. For example, assume that the voltage applied to the motor terminals at start-up is reduced to 50% of the rated nameplate voltage. The magnetizing flux of the stator is also reduced to half of the normal value. The voltages and currents induced in the rotor are similarly reduced by half. The resulting torque output of the motor is reduced to one-fourth of its original value. Figure 16–4 shows that a 50% reduction in voltage causes the torque to decrease to 25% of its normal value.

The torque formula given previously shows why the large reduction in the torque out- put occurs. Both the stator flux (<P S ) and the rotor current (IR ) are reduced to half of their original values. This means that the product (torque) of these terms is only one-fourth of

its original value. For a given value of slip, the torque varies as the square of the impressed voltage.

As explained previously, an increase in slip increases the rotor frequency and the inductive reactance of the rotor. In the normal operating range of the motor from no load to full load, the rotor frequency seldom is greater than 2 to 3 Hz. Therefore, a change in the frequency has negligible effects on the impedance of the rotor at full load, and even at 125% of the rated load.

Motor with Overload

When a motor has a heavy overload, the percent slip will increase, causing an increase in the rotor frequency. The increased frequency causes an increase in the inductive reactance and the impedance of the rotor circuit. Two effects result from the increase in the inductive reactance of the rotor circuit. First, the power factor of the rotor decreases, causing the rotor current to lag the induced rotor voltage. The rotor field flux will not reach its maximum value until the peak value of the stator flux wave has passed it. Although the cur- rents in the stator and rotor circuits increase because of the overload, the fluxes of the stator and the rotor fields are out of phase with each other. Therefore, there is less interaction

between the fields and the torque decreases. The second effect is that the increase in the inductive reactance and the impedance of the rotor decrease the rate at which the rotor current increases with an increase in slip. Because of these two effects, the torque increase will be less rapid. The torque reaches its maximum value at approximately 20% slip in the typical squirrel-cage induction motor.

Breakdown Torque

In Figure 16–4, note that the torque curve increases as a straight line well beyond the rated load. As the percent slip increases between 10% and 20%, there is a reduction in the rate at which the torque increases. Finally, at approximately 20% slip, the torque reaches its maximum value. The point of the maximum torque output is called the breakdown point. An increase in the load beyond this point results in less torque being developed by the motor and the rotor stops. As shown in the figure, this breakdown point is reached between 200% and 300% of the rated torque.

The following example shows that for a given value of slip, the torque varies as the square of the impressed voltage. Assume that a 240-V, squirrel-cage motor is operated on a 208-V, three-phase circuit. The value of 208 V is 87% of the rated voltage of the motor. The torque output is 0.872 = 0.75. This means that the breakdown torque is reduced to 75% of its rated value.

SYNCHRONOUS SPEED

The speed at which the magnetic field rotates is known as the synchronous speed. The synchronous speed of a three-phase motor is determined by two factors:

1. The number of stator poles

2. The frequency of the ac line

Because 60 Hz is a standard frequency throughout the United States and Canada, the following gives the synchronous speeds for motors with different numbers of poles:

Speed Performance

The field set up by the stator windings cuts the copper bars of the rotor. Voltages induced in the squirrel-cage winding set up currents in the rotor bars. As a result, a field is created on the rotor core. The attraction between the stator field and the rotor field causes the rotor to follow the stator field. The rotor always turns at a speed that is slightly less than that of the stator field (less than the synchronous speed). In this way, the stator field cuts the rotor bars and induces the necessary rotor voltages and currents to create the rotor field.

The torque produced by an induction motor results from the interaction between the stator flux and the rotor flux. If the rotor is turned at the same speed as the stator field, there will be no relative motion between the rotor bars and the stator field. This means that no torque can be produced. A torque is produced only when the rotor turns at a speed that is less than synchronous speed. At no load, the mechanical losses of the motor can be over- come by a small torque. The rotor speed will be slightly less than the synchronous speed of the stator field.

As a mechanical load is applied to the motor shaft, the rotor speed will decrease. The stator field turns at a constant synchronous speed and cuts the rotor bars at a faster rate per second. The voltages and currents induced in the rotor bars increase accordingly, causing a greater induced rotor voltage. The resulting increase in the rotor current causes a large torque at a slightly lower speed.

The squirrel-cage winding was described as consisting of heavy copper bars welded to two end rings. The impedance of this winding is relatively low. Therefore, a slight decrease in the speed causes a large increase in the currents in the rotor bars. Because the rotor circuit of a squirrel-cage induction motor has a low impedance, the speed regulation of this motor is very good.

PERCENT SLIP

The speed performance of squirrel-cage induction motors is measured in terms of percent slip. In determining percent slip, the synchronous speed of the stator field is used as a reference point. The synchronous speed for a particular motor is constant, because the number of poles and the frequency remain the same. Slip is the number of revolutions per minute by which the rotor falls behind the speed of the rotating field of the stator. Slip is determined by subtracting the speed of the rotor from the synchronous speed of the stator field. For example, a three-phase, two-pole induction motor has a full-load speed of 3480 r/min. The synchronous speed of the stator field is

Smaller values of percent slip mean that the motor has better speed regulation. When determined at the rated load, the percent slip of most squirrel-cage induction motors varies from 2% to 5%. This type of motor is considered to be a constant-speed motor because there is a small decrease in the speed between the no-load and full-load points.

ROTOR FREQUENCY

In the previous example, the rotor slips behind the speed of the stator field by 120 revolutions per minute. The flux of the two stator poles passes a given rotor bar of the squirrel-cage winding only 120 times every minute. Thus, the voltages and currents induced in the rotor will have a very low frequency. The rotor frequency is

Unit 1 showed that when a conductor passes a pair of unlike poles, one cycle (Hz) of voltage is induced in the conductor. In this example, a pair of stator poles passes a given bar in the squirrel-cage rotor 120 times per minute or twice per second. Thus, the frequency must be 2 Hz. If the slip is increased, the rotor frequency will increase, because the flux of the revolving field will cut a given bar in the squirrel-cage winding more times per second. This relationship can be expressed as a formula

Note that methods 1 and 2 both give the same frequency for the rotor. This frequency is an important factor in the operation of the motor. A change in the rotor frequency causes a change in the inductive reactance component (X= 2Tif L) of the rotor impedance. Thus, a change in the frequency will affect the starting and running characteristics of the motor.

PROBLEM 1

Statement of the Problem

A 5-hp, 220-V, three-phase, 60-Hz, squirrel-cage induction motor has eight poles. At the rated load, it has a speed of 870 r/min. Determine

1. the synchronous speed.

2. the percent slip, at the rated load.

3. the rotor frequency, at the instant of start-up.

4. ssthe rotor frequency, at the rated load.

Solution

1. The synchronous speed of the stator field is found using the frequency formula trans- posed to solve for S:

2. At the rated load, the percent slip is

3. At start-up, the rotor is not turning. The slip at this instant is unity, or 100%. There- fore, the rotor frequency and the stator frequency are both 60 Hz.

4. The rotor turns at 870 r/min at the rated load. The rotor frequency at this speed can be determined as follows:

Method 1:

Slip, in r/min = synchronous speed – rotor speed

= 900 – 870 = 30 r/min

TORQUE AND SPEED CHARACTERISTICS

The torque produced by an induction motor depends on the strengths of the stator and rotor fields and the phase relationship between the fields:

This torque formula is similar to the formula for the torque of a dc motor: T = k X 8f X IA. The difference between the formulas is in the cos 8R function. The equivalent dia- gram of the rotor is an inductor and resistor in series. Because rotor frequency is a function of slip, it follows that cos 8R varies with slip.

STARTING CHARACTERISTICS

At the instant the motor is started, the rotor is not turning and there is 100% slip. The rotor frequency at this moment is equal to the stator frequency. The inductive reactance of the rotor is very large compared to the effective resistance component. Also, the rotor has a very low lagging power factor. This means that the rotor flux lags the stator flux by a large phase angle. As a result, the interaction between the two fields is small and the starting torque is low.

As the speed of the motor increases, the percent slip and the frequency of the rotor decrease. The decrease in the rotor frequency causes the inductive reactance and the impedance of the rotor to decrease. Thus, the phase angle between the stator and rotor fluxes is reduced. The torque then increases to its maximum value at about 20% slip. As the rotor continues to accelerate, the torque decreases until it reaches the value required to turn the mechanical load applied to the motor shaft. The slip at this point is between 2% and 5%.

Starting Current

At start-up the stator field cuts the rotor bars at a faster rate than when the rotor is turning. The large voltage induced in the rotor causes a large rotor current. As a result, the stator current will also be high at start-up. The squirrel-cage induction motor resembles a static transformer during this brief instant. That is, the stator may be viewed as the primary or input winding, and the squirrel-cage rotor winding as the secondary winding.

Most three-phase, squirrel-cage induction motors are started with the rated line voltage applied directly to the motor terminals. This means that the starting surge of current reaches a value as high as three to five times the full-load current rating of the motor. This high starting current requires induction motors to have starting protection. This protection may be rated as high as three times the full-load current rating of the motor. In some instances, very large induction motors are started with auxiliary starters. These devices reduce the motor voltage at start-up to limit the starting surge of current. As a result, there is less voltage disturbance on the feeder circuit supplying the motor load.

Starting with Reduced Voltage

There are problems in starting a large induction motor with a reduced voltage. For example, assume that the voltage applied to the motor terminals at start-up is reduced to 50% of the rated nameplate voltage. The magnetizing flux of the stator is also reduced to half of the normal value. The voltages and currents induced in the rotor are similarly reduced by half. The resulting torque output of the motor is reduced to one-fourth of its original value. Figure 16–4 shows that a 50% reduction in voltage causes the torque to decrease to 25% of its normal value.

The torque formula given previously shows why the large reduction in the torque out- put occurs. Both the stator flux (<P S ) and the rotor current (IR ) are reduced to half of their original values. This means that the product (torque) of these terms is only one-fourth of

its original value. For a given value of slip, the torque varies as the square of the impressed voltage.

As explained previously, an increase in slip increases the rotor frequency and the inductive reactance of the rotor. In the normal operating range of the motor from no load to full load, the rotor frequency seldom is greater than 2 to 3 Hz. Therefore, a change in the frequency has negligible effects on the impedance of the rotor at full load, and even at 125% of the rated load.

Motor with Overload

When a motor has a heavy overload, the percent slip will increase, causing an increase in the rotor frequency. The increased frequency causes an increase in the inductive reactance and the impedance of the rotor circuit. Two effects result from the increase in the inductive reactance of the rotor circuit. First, the power factor of the rotor decreases, causing the rotor current to lag the induced rotor voltage. The rotor field flux will not reach its maximum value until the peak value of the stator flux wave has passed it. Although the cur- rents in the stator and rotor circuits increase because of the overload, the fluxes of the stator and the rotor fields are out of phase with each other. Therefore, there is less interaction

between the fields and the torque decreases. The second effect is that the increase in the inductive reactance and the impedance of the rotor decrease the rate at which the rotor current increases with an increase in slip. Because of these two effects, the torque increase will be less rapid. The torque reaches its maximum value at approximately 20% slip in the typical squirrel-cage induction motor.

Breakdown Torque

In Figure 16–4, note that the torque curve increases as a straight line well beyond the rated load. As the percent slip increases between 10% and 20%, there is a reduction in the rate at which the torque increases. Finally, at approximately 20% slip, the torque reaches its maximum value. The point of the maximum torque output is called the breakdown point. An increase in the load beyond this point results in less torque being developed by the motor and the rotor stops. As shown in the figure, this breakdown point is reached between 200% and 300% of the rated torque.

The following example shows that for a given value of slip, the torque varies as the square of the impressed voltage. Assume that a 240-V, squirrel-cage motor is operated on a 208-V, three-phase circuit. The value of 208 V is 87% of the rated voltage of the motor. The torque output is 0.872 = 0.75. This means that the breakdown torque is reduced to 75% of its rated value.

Three-Phase Induction Motors

THREE-PHASE, SQUIRREL-CAGE INDUCTION MOTOR

A three-phase, squirrel-cage induction motor is shown in Figure 16–1. This motor is simple in construction and is easy to maintain. For a given horsepower rating, the physical size of this motor is small, when compared with other types of motors. It has very good speed regulation under varying load conditions. This motor is used for many industrial applications because of its low purchase price, rugged construction, and operating characteristics.

Construction

The basic structure of a three-phase, squirrel-cage induction motor consists of a stator, a rotor, and two end shields that house the bearings supporting the rotor shaft.

The stator is a three-phase winding that is placed in the slots of a laminated steel core. The winding itself is made of formed coils that are connected to give three single-phase windings spaced 120 electrical degrees apart. The three separate single-phase windings are connected in wye or delta. Three line leads from the three-phase stator windings are brought out to a terminal box mounted on the frame of the motor.

The rotor has a cylindrical core consisting of steel laminations (Figure 16–2). Aluminum bars are mounted near the surface of the rotor. These bars are brazed or welded to two aluminum end rings. Some types of squirrel-cage induction motors are smaller than others

and have aluminum end rings that are cast in one piece. The rotor shaft is supported by bearings housed in the end shields.

THE ROTATING MAGNETIC FIELD

The principle of operation for all three-phase motors is the rotating magnetic field. There are three factors that cause the magnetic field to rotate:

1. The fact that the voltages of a three-phase system are 120° out of phase with each other

2. The fact that the three voltages change polarity at regular intervals

3. The arrangement of the stator windings around the inside of the motor

Figure 16–3A shows three ac voltages 120° out of phase with each other, and the stator winding of a three-phase motor. The stator illustrates a two-pole, three-phase motor.

Two-pole means that there are two poles per phase. AC motors seldom have actual pole pieces as shown in Figure 16–3A, but they will be used here to aid in understanding how the rotating magnetic field is created in a three-phase motor. Notice that pole pieces 1A and 1B are located opposite each other. The same is true for poles 2A and 2B, and 3A and 3B. Pole pieces 1A and 1B are wound with wire that is connected to phase 1 of the three-phase system. Notice also that the pole pieces are wound in such a manner that they will always have opposite magnetic polarities. If pole piece 1A has a north magnetic polarity, pole piece 1B will have a south magnetic polarity at the same time.

The windings of pole pieces 2A and 2B are connected to line 2 of the three- phase system. The windings of pole pieces 3A and 3B are connected to line 3 of the three-phase system. These pole pieces are also wound in such a manner as to have the opposite polarity of magnetism.

To understand how the magnetic field rotates around the inside of the motor, refer to Figure 16–3B. Notice that a line labeled A has been drawn through the three voltages of the system. This line is used to illustrate the condition of the three voltages at this point in time. The arrow drawn inside the motor indicates the greatest strength of the magnetic field at the same point in time. It is to be assumed that the arrow is pointing in the direction of the north magnetic field. Notice in Figure 16–3B that phase 1 is at its maximum positive peak and that phases 2 and 3 are less than maximum. The magnetic field is, therefore, strongest between pole pieces 1A and 1B.

In Figure 16–3C, line B indicates that the voltage of line 3 is zero. The voltage of line 1 is less than maximum positive, and line 2 is less than maximum negative. The magnetic field at this point is concentrated between the pole pieces of phases 1 and 2.

In Figure 16–3D, line C indicates that line 2 is at its maximum negative peak and that lines 1 and 3 are less than maximum positive. The magnetic field at this point is concentrated between pole pieces 2A and 2B.

In Figure 16–3E, line D indicates that line 1 is zero. Lines 2 and 3 are less than maxi- mum and in opposite directions. At this point in time, the magnetic field is concentrated between the pole pieces of phase 2 and phase 3.

In Figure 16–3F, line E indicates that phase 3 is at its maximum positive peak, and lines 1 and 2 are less than maximum and in the opposite direction. The magnetic field at this point is concentrated between pole pieces 3A and 3B.

In Figure 16–3G, line F indicates that phase 2 is zero. Line 3 is less than maximum positive, and line 1 is less than maximum negative. The magnetic field at this time is concentrated between the pole pieces of phase 1 and phase 3.

In Figure 16–3H, line G indicates that phase 1 is at its maximum negative peak, and phases 2 and 3 are less than maximum and in the opposite direction. Notice that the magnetic field is again concentrated between pole pieces 1A and 1B. This time, however, the magnetic polarity is reversed because the current has reversed in the stator winding.

In Figure 16–3I, line H indicates that phase 2 is at its maximum positive peak and phases 1 and 3 are less than maximum and in the negative direction. The magnetic field is concentrated between pole pieces 2A and 2B.

In Figure 16–3J, line I indicates that phase 3 is maximum negative, and phases 1 and 2 are less than maximum in the positive direction. The magnetic field at this point is concentrated between pole pieces 3A and 3B.

In Figure 16–3K, line J indicates that phase 1 is at its positive peak, and phases 2 and 3 are less than maximum and in the opposite direction. The magnetic field is again concentrated between pole pieces 1A and 1B. Notice that in one complete cycle of the three-phase voltage, the magnetic field has rotated 360° around the inside of the stator winding.

If any two of the stator leads is connected to a different line, the relationship of the voltages will change and the magnetic field will rotate in the opposite direction. The direction of rotation of a three-phase motor can be reversed by changing any two stator leads.