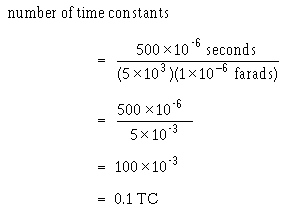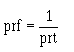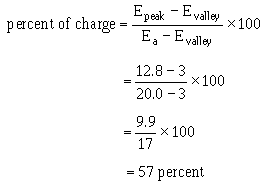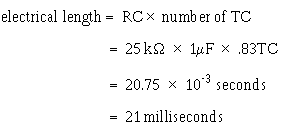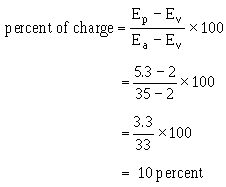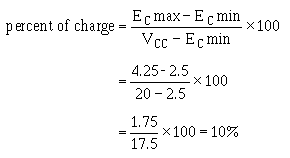TIME-BASE GENERATORS
Radar sets, oscilloscopes, and computer circuits all use sawtooth (voltage or current) waveforms. A sawtooth waveshape must have a linear rise. The sawtooth waveform is often used to produce a uniform, progressive movement of an electron beam across the face of an electrostatic cathode ray tube. This movement of the electron beam is known as a SWEEP. The voltage which causes this movement is known as SWEEP VOLTAGE and the circuit which produces this voltage is the SWEEP GENERATOR, or TIME-BASE GENERATOR. Most common types of time-base generators develop the sawtooth waveform by using some type of switching action with either the charge or discharge of an RC or RL circuit.
Sawtooth Wave
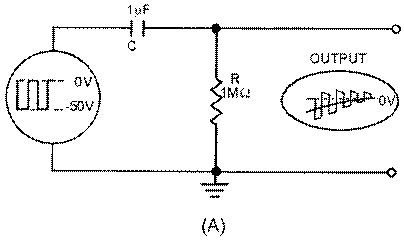
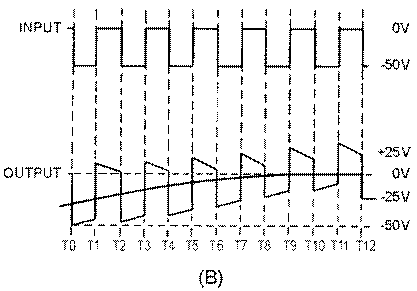
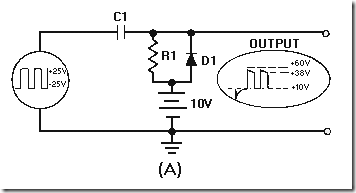
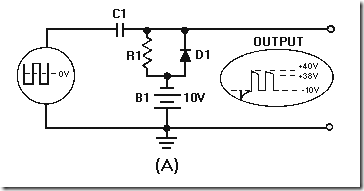
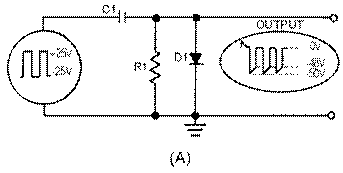
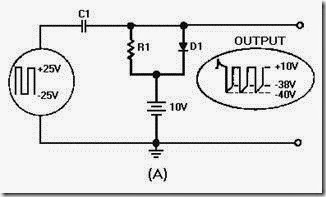
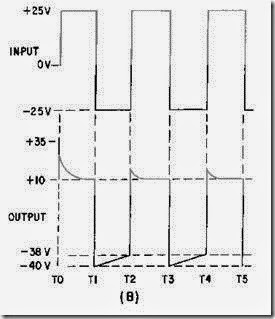
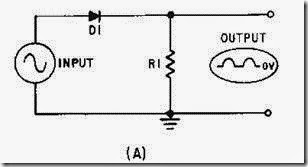
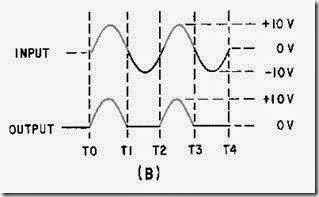
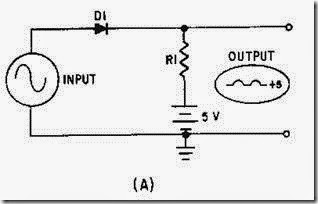
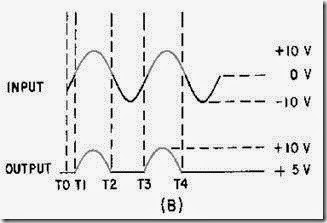
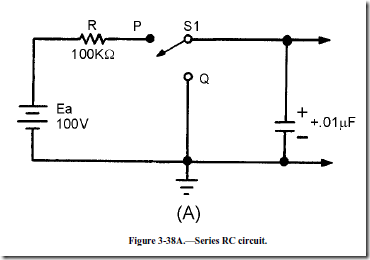
A sawtooth wave can be generated by using an RC network. Possibly the simplest sawtooth generator is that which is shown in figure 3-38, view (A). Assume that at T0 (view (B)), S1 is placed in position P. At the instant the switch closes, the applied voltage (Ea) appears at R. C begins to charge to E a through R. If S1 remains closed long enough, C will fully charge to Ea. You should remember from NEETS, Module 2, Alternating Current and Transformers, that a capacitor takes 5 time constants (5TC) to fully charge. As the capacitor charges to the applied voltage, the rate of charge follows an exponential curve. If a linear voltage is desired, the full charge time of the capacitor cannot be used because the exponential curve becomes nonlinear during the first time constant.
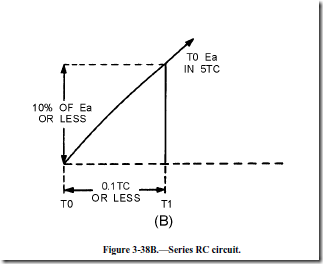
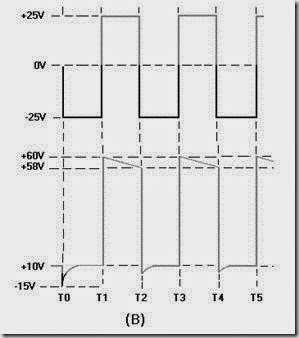
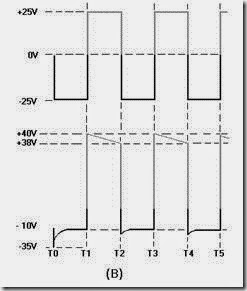
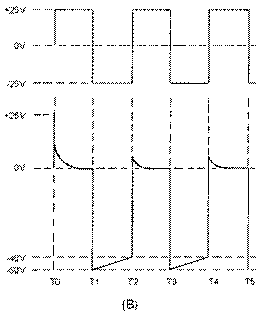
However, during the first 10 percent of the first time constant, the rate of voltage change across the capacitor is almost constant (linear). Suppose that S1 is placed in position P at T0, and C is allowed to charge for 0.1 time constant. This is shown as T0 to T1 in view (B). Notice that the rate of voltage change across C is nearly constant between T0 and T1. Now, assume that at T1 the switch is moved from position P to position Q. This shorts the capacitor, and it discharges very rapidly. If the switch is placed back in position P, the capacitor will start charging again.
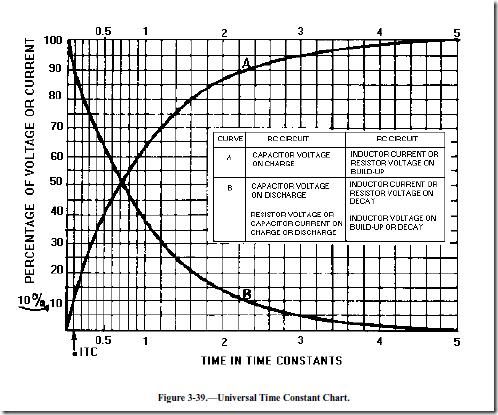
By selecting the sizes of R and C, you can have a time constant of any value you desire. Further, by controlling the time S1 remains closed, you can generate a sawtooth of any duration. Figure 3-39 is the Universal Time Constant Chart. Notice in the chart that if 1 time constant is 1,000 microseconds, S1 (figure 3-38, view (A )) can be closed no longer than 100 microseconds to obtain a reasonable linear sawtooth. In this example, C1 will charge to nearly 10 volts in 0.1 time constant.
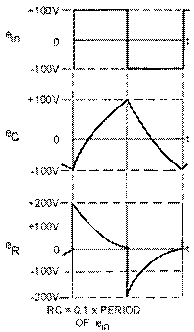
 The dimensions of the sawtooth waveform used in oscilloscopes need to be discussed before going any further. Figure 3-40 shows a sawtooth waveform with the various dimensions labeled. The duration of the rise of voltage (T0 to T1) is known as the SWEEP TIME or ELECTRICAL LENGTH. The electron beam of an oscilloscope moves across the face of the cathode ray tube during this sweep time. The amount of voltage rise per unit of time is referred to as the SLOPE of the waveform. The time from T1 to T2 is the capacitor discharge time and is known as FALL TIME or FLYBACK TIME. This discharge time is known as flyback time because during this period the electron beam returns, or "flys" back, from the end of a scanning line to begin the next line.
The dimensions of the sawtooth waveform used in oscilloscopes need to be discussed before going any further. Figure 3-40 shows a sawtooth waveform with the various dimensions labeled. The duration of the rise of voltage (T0 to T1) is known as the SWEEP TIME or ELECTRICAL LENGTH. The electron beam of an oscilloscope moves across the face of the cathode ray tube during this sweep time. The amount of voltage rise per unit of time is referred to as the SLOPE of the waveform. The time from T1 to T2 is the capacitor discharge time and is known as FALL TIME or FLYBACK TIME. This discharge time is known as flyback time because during this period the electron beam returns, or "flys" back, from the end of a scanning line to begin the next line.
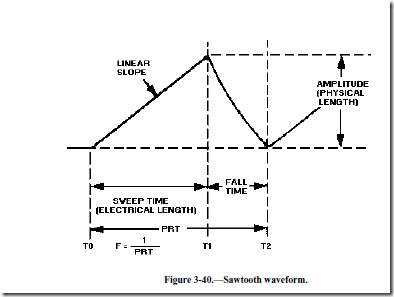
The amplitude of the rise of voltage is known as the PHYSICAL LENGTH. It is called physical length because the greater the peak voltage, the greater physical distance the beam will move. For example, the amount of voltage needed to move an electron beam 4 inches is twice the amount needed to move the beam 2 inches across the face of a given crt.
The voltage rise between T0 to T1 is the LINEAR SLOPE of the wave. The linearity of the rise of voltage is determined by the amount of time the capacitor is allowed to charge. If the charge time is kept short (10 percent or less of 1TC), the linearity is reasonably good.
As stated in the discussion of time-base generators, the waveform produced from any sawtooth generator must be linear. A LINEAR SAWTOOTH is one that has an equal change in voltage for an equal change in time. Referring to the Universal Time Constant Chart in figure 3-39, you can see that the most desirable part of the charge curve is the first one-tenth (0.1) of the first TC.
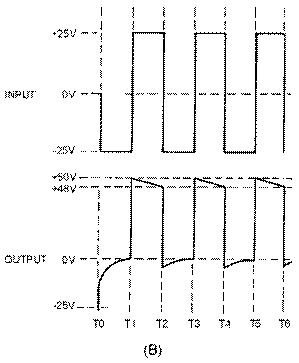
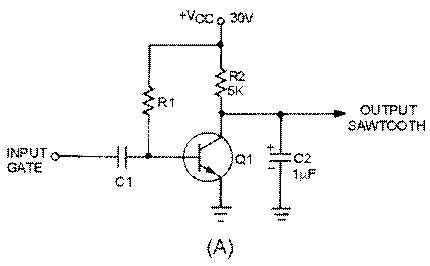
Figure 3-41, view (A), is a transistor sawtooth generator. In this figure R1 is a forward-biasing resistor for Q1, C1 is a coupling capacitor, and Q1 is serving as a switch for the RC network consisting of R2 and C2. With forward bias applied to Q1, the generator conducts at saturation, and its collector voltage (the output) is near 0 volts as indicated by the waveform in view (B). The charge felt by C1 is nearly 0. A negative gate is applied to the base of Q1 to cut off Q1 and allow C2 to charge. The length of time that the gate is negative determines how long Q1 will remain cut off and, in turn, how long C2 will be allowed to charge. The length of time that C2 is allowed to charge is referred to as the electrical length of the sawtooth that is produced.
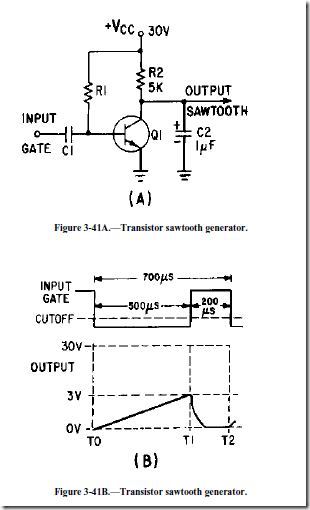
The amplitude of the sawtooth that is produced is limited by the value of VCC that is used in the circuit. For example, if the voltage is 30 volts, and the capacitor (C2) is allowed to charge to 10 percent of 30 volts, then the amplitude of the sawtooth will be 3 volts (see figure 3-41, view (B)). If VCC is increased to 40 volts, C2 will charge to 10 percent of 40 volts and the output will increase in amplitude to 4 volts. Changing the value of V CC in the circuit changes the amplitude of the sawtooth waveform that is produced; amplitude determines the physical length. Since the number of time constants used in the circuit has not been changed, linearity does not change with a change in VCC.
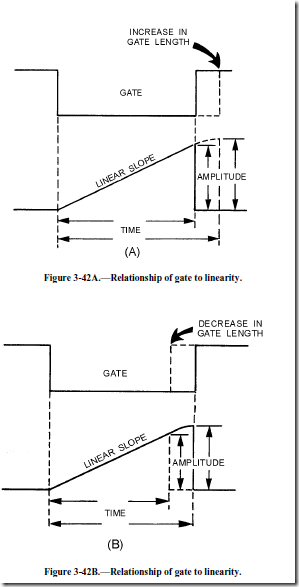
The linear slope that is produced by the circuit is dependent on two variables; (1) the time constant of the RC circuit and (2) the gate length of the gate applied to the circuit. The circuit will produce a linear sawtooth waveshape if the components selected are such that only one-tenth of 1 TC or less is used. The GATE LENGTH is the amount of time that the gate is applied to the circuit and controls the time that the capacitor is allowed to charge. The value of R2 and C2 determines the time for 1 time constant (TC = RC). To determine the number of time constants (or the fraction of 1TC) used, divide the time for 1 time constant into the time that the capacitor is allowed to charge:

In figure 3-41, view (B), gate length is 500 microseconds and TC is the product of R2 (5 kilohms) and C2 (1 microfarad). The number of time constants is computed as follows:
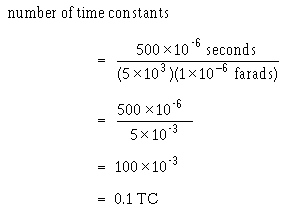
Therefore, 0.1TC is the length of time required to produce a linear rise in the sawtooth waveform.

shows that an increase in gate length increases the number of time constants. An increase in the number of time constants decreases linearity. The reason is that C2 now charges to a greater percentage of the applied voltage, and a portion of the charge curve is being used that is less linear. The waveform in figure 3-42, view (A), shows an increase in amplitude (physical length), an increase in the time that C2 is allowed to charge (electrical length), and a decrease in linearity. If a smaller percentage of VCC is used, the gate length is decreased. As shown in view (B), this decreased gate length results in an increase in linearity, a decrease in the time that C2 is allowed to charge (electrical length), and a decrease in amplitude (physical length).
Changing the value of R and C in the circuit affects linearity since they control the time for 1 time constant. For example, if the value of C2 is increased in the circuit, as shown in figure 3-43, view (A), the time for 1 time constant increases and the number of time constants then decreases. With a decrease in the number of time constants, linearity increases. The reason is that a smaller percentage of VCC is used, and the circuit is operating in a more linear portion of the charge curve. Increasing the value of the TC (C2 or R2) decreases the amplitude of the sawtooth (physical length) because C2 now charges to a smaller percentage VCC for a given time. The electrical length remains the same because the length of time that C2 is allowed to charge has not been changed.
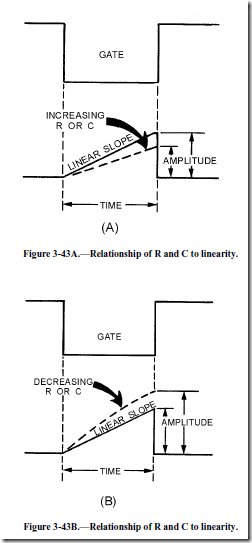
Decreasing the value of the TC (R2 or C2), as shown in figure 3-43, view (B), results in an increase in the number of time constants and therefore causes linearity to decrease. Anytime the number of time constants increases, the percentage of charge increases (see the Universal Time Constant Chart, figure 3- 39), and amplitude (physical length) increases. Without an increase in gate length, the time that C2 is allowed to charge through R2 remains the same; therefore, electrical length remains the same. Linearity is affected by gate length, the value of R, and the value of C; but is not affected by changing the value of VCC. Increasing the gate length decreases linearity, and decreasing gate length increases linearity. Increasing R or C in the circuit increases linearity, and decreasing R or C in the circuit decreases linearity.
The entire time of the sawtooth, from the time at which the capacitor begins charging (T0 in figure 3-41, view (B)) to the time when it starts charging again (T2), is known as the prt of the wave. The pulse repetition frequency of the sawtooth wave is:
UNIJUNCTION SAWTOOTH GENERATOR.—So far, you have learned in this chapter that a switch and an RC network can generate a sawtooth waveform. When using a unijunction transistor as the switch, a simple sawtooth generator looks like the circuit in figure 3-44, view (A); the output waveshapes are shown in view (B). You may want to review unijunction transistors in NEETS, Module 7, Introduction to Solid-State Devices and Power Supplies, chapter 3, before continuing.
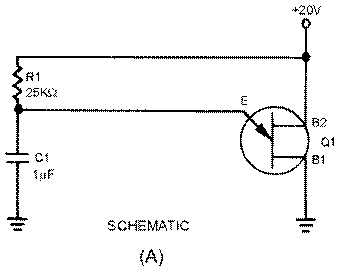
Figure 3-44A.—Unijunction sawtooth generator. SCHEMATIC.
When the 20 volts is applied across B2 and B1, the n-type bar acts as a voltage- divider. A voltage of 12.8 volts appears at a point near the emitter. At the first instant, C1 has no voltage across it, so the output of the circuit, which is taken across the capacitor (C1), is equal to 0 volts. (The voltage across C1 is also the voltage that is applied to the emitter of the unijunction.) The unijunction is now reverse biased. After T0, C1 begins to charge toward 20 volts.
At T1, the voltage across the capacitor (the voltage on the emitter) has reached approximately 12.8 volts. This is the peak point for the unijunction, and it now becomes forward biased. With the emitter forward biased, the impedance between the emitter and B1 is just a few ohms. This is similar to placing a short across the capacitor. The capacitor discharges very rapidly through the low resistance of B1 to E.
As C1 discharges, the voltage from the emitter to B1 also decreases. Q1 will continue to be forward biased as long as the voltage across C1 is larger than the valley point of the unijunction.
At T2 the 3-volt valley point of the unijunction has been reached. The emitter now becomes reverse biased and the impedance from the emitter to B1 returns to a high value. Immediately after T2, Q1 is reverse biased and the capacitor has a charge of approximately 3 volts. C1 now starts to charge toward 20 volts as it did originally (just after T0). This is shown from T2 to T3 in figure 3-44, view (B).
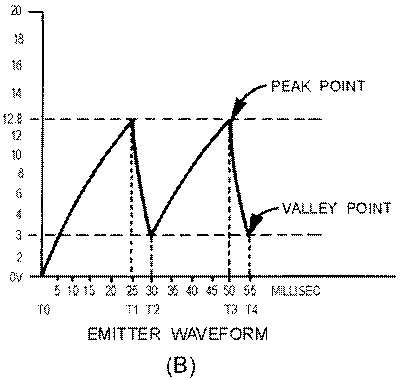
Figure 3-44B.—Unijunction sawtooth generator. EMITTER WAVEFORM.
The circuit operation from now on is just a continuous repetition of the actions between T2 and T4. The capacitor charges until the emitter becomes forward biased, the unijunction conducts and C1 discharges, and Q1 becomes reverse biased and C1 again starts charging.
Now, let’s determine the linearity, electrical length, and amplitude of the output waveform. First, the linearity: To charge the circuit to the full 20 volts will take 5 time constants. In the circuit shown in figure 3-44, view (B), C1 is allowed to charge from T2 to T3. To find the percentage of charge, use the equation:
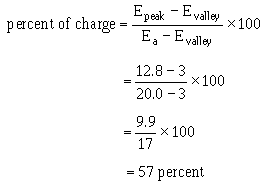
This works out to be about 57 percent and is far beyond the 10 percent required for a linear sweep voltage. The linearity is very poor in this example.
The electrical length (sweep time), which is measured from T2 to T3, can be found by multiplying RC times the number of time constants. Refer to the Universal Time Constant Chart (figure 3-39) again to find that 57 percent is 0.83TC. By multiplying 0.83 times R1C1, you will find that the electrical length is approximately 21 milliseconds:
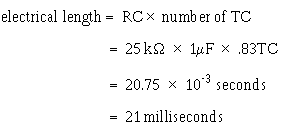
The physical length (amplitude) is determined by subtracting the valley point from the peak point. This is 9.8 volts in the example (12.8 volts – 3 volts).
For a sweep generator that produces a more linear output sawtooth waveform, refer to the circuit in figure 3-45, view (A). R1 and C1 form the RC time constant. Notice that the capacitor charges toward 35 volts (VE) in this circuit.
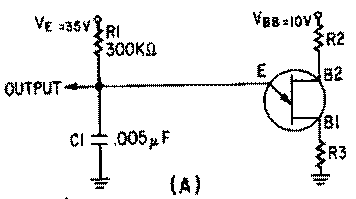
Figure 3-45A.—Improved unijunction sawtooth generator.
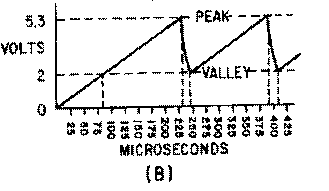
Figure 3-45B.—Improved unijunction sawtooth generator.
The output waveform is shown in figure 3-45, view (B). With a lower voltage applied from B1 to B2, the peak and valley points are closer together. Calculating the percentage of charge:
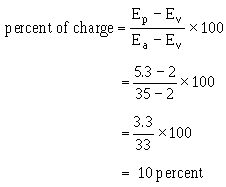
The linearity in this case is good. Using the Universal Time Constant Chart, a 10-percent charge amounts to 0.1 time constant. The electrical length is, again, RC times the number of time constants. With R1 at 300 kilohms and C1 at .005 microfarads, the time constant is 1,500 microseconds. One-tenth of a time constant is equal to 150 microseconds; so the electrical length is 150 microseconds. Prt is the electrical length plus the fall or flyback time. If C1 discharges from 5.3 volts to 2 volts in 15 microseconds, then the prt is 150 + 15, or 165 microseconds. The prf is about 6 kilohertz
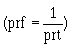
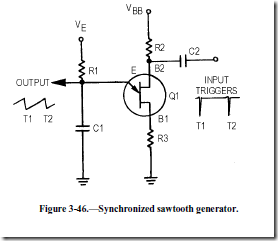
Some unijunction circuits are triggered to obtain a very stable prf. One method is to apply triggers to B2, as shown in figure 3-46. Negative triggers applied to B2 reduce the inter-base voltage enough to cause a forward bias condition in the emitter circuit. This cuts off the sweep and allows C1 to discharge through the B1-to-emitter circuit. Then, C1 recharges until the next trigger arrives and C1 discharges. Circuit operation and parameters are figured in the same manner as in the previous sawtooth circuits.
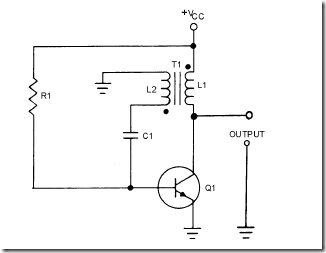
TRANSISTOR SAWTOOTH GENERATOR.—The next sawtooth generator uses a conventional pnp transistor, as shown in figure 3-47, view (A). This generator also uses an RC network, and the transistor provides the switching action.
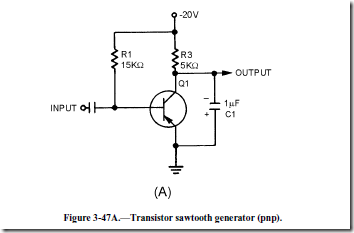
The waveforms for the circuit are shown in views (B) and (C). With no input signals, Q1 is biased near saturation by R1. The voltage across C1 is very low (-2.5 volts) because load resistor R3 drops most of the applied voltage. The transistor must be cut off to allow C1 to charge. To cut off Q1, a positive rectangular wave is used.
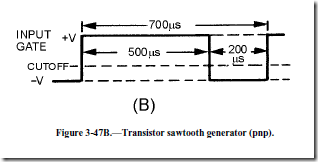
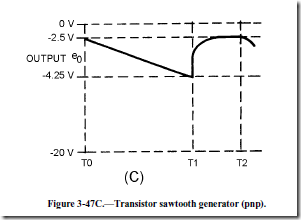
Since Q1 is a pnp transistor, a positive voltage must be used to drive it to cutoff. Figure 3-47, view (B), shows a rectangular wave input 500 microseconds long on the positive alternation. At T0, the positive gate applied to the base of Q1 cuts off Q1. This effectively removes the transistor from the circuit (opens the switch), and C1 charges through R3 toward 20 volts. Starting with a charge of -2.5 volts at T0, C1 charges (T0 to T1) for 500 microseconds to -4.25 volts at T1. Let’s determine the percent of charge:
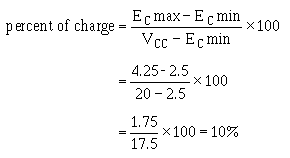
This allows nearly a linear rise of voltage across C1.
Increasing the value of R3 or C1 increases the time constant. The capacitor will not charge to as high a voltage in the same period of time. Decreasing the width of the gate and maintaining the same time constant also prevents the capacitor from charging as much. With less charge on the capacitor, and the same voltage applied, linearity has been improved. Decreasing R3 or C1 or increasing gate width decreases linearity. Changing the applied voltage will change the charge on the capacitor. The percentage of charge remains constant; however, it does not affect linearity.
At T1, the positive alternation of the input gate ends, and Q1 returns to a forward-bias condition. A transistor that is near saturation has very low resistance, so C1 discharges rapidly between T1 and T2, as shown in figure 3-47, view (C). The capacitor discharges in less than 200 microseconds, the length of the negative alternation of the gate. The negative gate is made longer than the discharge time of the capacitor to ensure that the circuit has returned to its original condition.
From T1 to T2, the capacitor discharges and the circuit returns to its original condition, ready for another positive gate to arrive. The next positive gate arrives at T2 and the actions repeats.
The amplitude of the output sawtooth wave is equal to 1.75 volts (4.25 volts minus 2.5 volts). The electrical length is the same as the positive alternation of the input gate, or 500 microseconds. The prt is 700 microseconds (500 + 200) and the prf is 1/prt or 1,428 hertz.
Trapezoidal Sweep Generator
Normally, oscilloscopes and synchroscopes use ELECTROSTATIC DEFLECTION and, as the name implies, electrostatic fields move the electron beam. The need here is for a sawtooth voltage waveform.
Another method of electron beam deflection is ELECTROMAGNETIC DEFLECTION. Currents through a coil produce electromagnetic fields which position the beam of electrons. The electromagnetic system requires a sawtooth of current which increases at a linear rate. Because of the inherent characteristics of a coil, a sawtooth voltage does not cause a linear increase of current. A linear increase of current requires a TRAPEZOIDAL voltage waveform applied to a coil. This section discusses the generation of a trapezoidal wave.
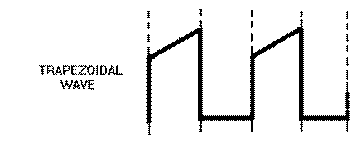
Figure 3-48 shows a trapezoidal wave. The wave consists of a sharp, almost instantaneous jump in voltage followed by a linear rise to some peak value. The initial change in voltage at T0 is called a JUMP or STEP. The jump is followed by a linear sawtooth voltage rise. The time from the jump to the peak amplitude is the sum of the jump voltage and the sawtooth peak; where the peak value occurs is the electrical length. The peak voltage amplitude is the sum of the jump voltage and the sawtooth peak voltage. The waveshape can be considered a combination of a rectangular wave and a sawtooth wave.
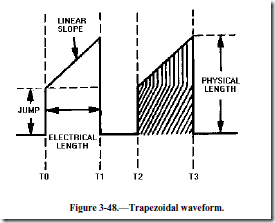 The inductance and resistance of a coil form a series RL circuit. The voltage drop across this inductance and resistance must be added to obtain the voltage waveform required to produce a linear rise in current. A linear rise of current produces a linear rise of voltage across the resistance of the coil and a constant voltage drop across the inductance of the coil.
The inductance and resistance of a coil form a series RL circuit. The voltage drop across this inductance and resistance must be added to obtain the voltage waveform required to produce a linear rise in current. A linear rise of current produces a linear rise of voltage across the resistance of the coil and a constant voltage drop across the inductance of the coil.
Assume figure 3-49, view (A), represents deflection coils. If we apply a voltage waveshape to the circuit, which will provide a square wave across inductor L, and a sawtooth across resistor R, then a linear current rise will result.
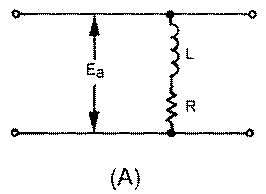
Figure 3-49A.—Series LR circuit.
View (B) of figure 3-49 shows the waveforms when Ea is a square wave. Recall that the inductor acts as an open circuit at this first instant. Current now starts to flow and develops a voltage across the resistor. With a square wave applied, the voltage across the inductor starts to drop as soon as any voltage appears across the resistor. This is due to the fact that the voltage across the inductor and resistor must add up to the applied voltage.
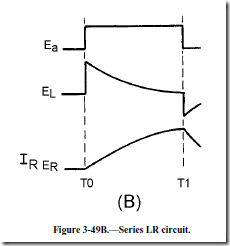
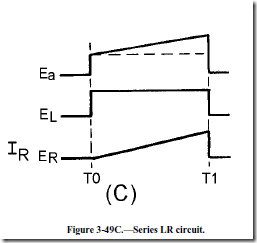
With Ea being a trapezoidal voltage, as shown in figure 3-49, view (C), the instant current flows, a voltage appears across the resistor, and the applied voltage increases. With an increasing applied voltage, the inductor voltage remains constant (EL) at the jump level and circuit current (I R) rises at a linear rate from the jump voltage point. Notice that if you add the inductor voltage (EL) and resistor voltage (ER) at any point between times T0 and T1, the sum is the applied voltage (Ea). The key fact here is that a trapezoidal voltage must be applied to a sweep coil to cause a linear rise of current. The linear rise of current will cause a uniform, changing magnetic field which, in turn, will cause an electron beam to move at a constant rate across a crt.
There are many ways to generate a trapezoidal waveshape. For example, the rectangular part could be generated in one circuit, the sawtooth portion in another, and the two combined waveforms in still a third circuit. A far easier, and less complex, way is to use an RC circuit in combination with a transistor to generate the trapezoidal waveshape in one stage.
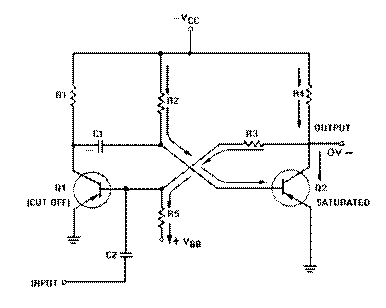
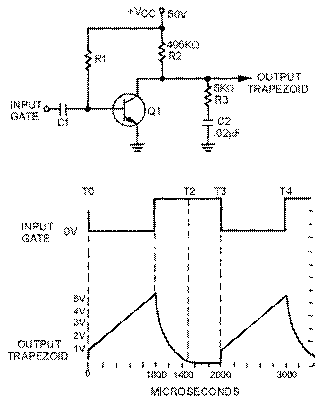
Figure 3-50, view (A), shows the schematic diagram of a trapezoidal generator. The waveshapes for the circuit are shown in view (B). R1 provides forward bias for Q1 and, without an input gate, Q1 conducts very hard (near saturation), C1 couples the input gate signal to the base of Q1. R2, R3, and C2 form the RC network which forms the trapezoidal wave. The output is taken across R3 and C2.
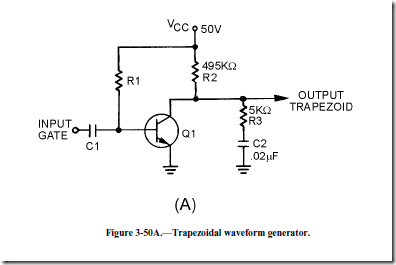
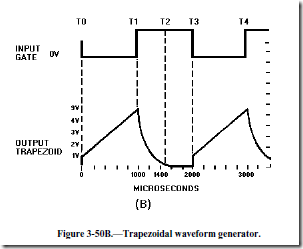
With Q1 conducting very hard, collector voltage is near 0 volts prior to the gate being applied. The voltage across R2 is about 50 volts. This means no current flows across R3, and C2 has no charge.
At T0, the negative alternation of the input gate is applied to the base of Q1, driving it into cutoff. At this time the transistor is effectively removed from the circuit. The circuit is now a series-RC network with 50 volts applied. At the instant Q1 cuts off, 50 volts will appear across the combination of R2 and R3 (the capacitor being a short at the first instant). The 50 volts will divide proportionally, according to the size of the two resistors. R2 then will have 49.5 volts and R3 will have 0.5 volt. The 0.5 volt across R3 (jump resistor) is the amplitude of the jump voltage. Since the output is taken across R3 and C2 in series, the output "jumps" to 0.5 volt.
Observe how a trapezoidal generator differs from a sawtooth generator. If the output were taken across the capacitor alone, the output voltage would be 0 at the first instant. But splitting the R of the RC network so that the output is taken across the capacitor and part of the total resistance produces the jump voltage.
Refer again to figure 3-50, view (A) and view (B). From T0 to T1, C2 begins charging toward 50 volts through R2 and R3. The time constant for this circuit is 10 milliseconds. If the input gate is 1,000 microseconds, the capacitor can charge for only 10 percent of 1TC, and the sawtooth part of the trapezoidal wave will be linear.
At T1, the input gate ends and Q1 begins to conduct heavily. C2 discharges through R3 and Q1. The time required to discharge C2 is primarily determined by the values of R3 and C2. The minimum discharge time (in this circuit) is 500 microseconds (5KW ´ .02µF ´ 5). At T2, the capacitor has discharged back to 0 volts and the circuit is quiescent. It remains in this condition until T3 when another gate is applied to the transistor.
The amplitude of the jump voltage was calculated to be 0.5 volt. The sawtooth portion of the wave is linear because the time, T0 to T1, is only 10 percent of the total charge time. The amplitude of the trapezoidal wave is approximately 5 volts. The electrical length is the same as the input gate length, or 1,000 microseconds. Linearity is affected in the same manner as in the sawtooth generator. Increasing R2 or C2, or decreasing gate width, will improve linearity. Changing the applied voltage will increase output amplitude, but will not affect linearity.
Linearity of the trapezoidal waveform, produced by the circuit in figure 3-50, view (A) and view (B) depends on two factors, gate length and the time constant of the RC circuit. Recall that these are the same factors that controlled linearity in the sawtooth generator. The formula developed earlier still remains true and enables us to determine what effect these factors have on linearity.

An increase in gate length results in an increase in the number of time constants and an increase in the percentage of charge that the capacitor will take on during this time interval. As stated earlier, if the number of time constants were to exceed 0.1, linearity would decrease. The reason for a decrease in linearity is that a greater percentage of VCC is used. The Universal Time Constant Chart (figure 3-39) shows that the charge line begins to curve. A decrease in gate length has the opposite effect on linearity in that it causes linearity to increase. The reason for this increase is that a smaller number of time constants are used and, in turn, a smaller percentage of the applied VCC is used.
Changing the value of resistance or capacitance in the circuit also affects linearity. If the value of C2 or R3 is increased, the time is increased for 1 time constant. An increase in the time for 1TC results in a decrease in the number of time constants required for good linearity. As stated earlier, a decrease in the number of time constants results in an increase in linearity (less than 0.1TC). In addition to an increase in jump voltage (larger value of R3) and a decrease in the amplitude (physical length) of the sawtooth produced by the circuit, electrical length remains the same because the length of the gate was not changed.
R2 has a similar effect on linearity because it is in series with R3. As an example, decreasing the value of R2 results in a decrease in linearity. The equation
![clip_image057[1] clip_image057[1]](http://lh5.ggpht.com/-KDuN1LAG-DE/VL1Gu8TscsI/AAAAAAABIeA/l70rNh3d4Ac/clip_image057%25255B1%25255D_thumb.gif?imgmax=800)
illustrates that by decreasing R (TC = RC), TC decreases and an increase in the number of time constants causes a decrease in linearity. Other effects are an increase in jump voltage and an increase in the amplitude (physical length) of the sawtooth.
Changing the value of VCC does not affect linearity. Linearity is dependent on gate length, R, and C. VCC does affect the amplitude of the waveform and the value of jump voltage that is obtained.
Q11. For an RC circuit to produce a linear output across the capacitor, the voltage across the capacitor may not exceed what percent of the applied voltage?
Q12. Increasing gate length in a sawtooth generator does what to linearity?
Q13. In a sawtooth generator, why is the transistor turned on for a longer time than the discharge time of the RC network?
Q14. What is added to a sawtooth generator to produce a trapezoidal wave?