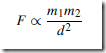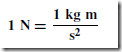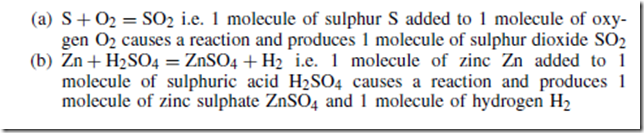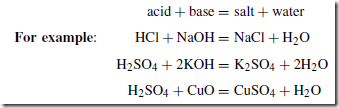science universe

Force, Mass and Acceleration

Introduction

When an object is pushed or pulled, a force is applied to the object. This force is measured in newtons (N). The effects of pushing or pulling an object are:

(i) to cause a change in the motion of the object, and

(ii) to cause a change in the shape of the object.

If a change occurs in the motion of the object, that is, its velocity changes from u to v, then the object accelerates. Thus, it follows that acceleration results from a force being applied to an object. If a force is applied to an object and it does not move, then the object changes shape, that is, deformation of the object takes place. Usually the change in shape is so small that it cannot be detected by just watching the object. However, when very sensitive measuring instruments are used, very small changes in dimensions can be detected.

A force of attraction exists between all objects. The factors governing the size of this force F are the masses of the objects and the distances between their centres:

Thus, if a person is taken as one object and the earth as a second object, a force of attraction exists between the person and the earth. This force is called the gravitational force and is the force that gives a person a certain weight when standing on the earth’s surface. It is also this force that gives freely falling objects a constant acceleration in the absence of other forces.

Newton’s Laws of Motion

To make a stationary object move or to change the direction in which the object is moving requires a force to be applied externally to the object. This concept is known as Newton’s first law of motion and may be stated as:

An object remains in a state of rest, or continues in a state of uniform motion in a straight line, unless it is acted on by an externally applied force

Since a force is necessary to produce a change of motion, an object must have some resistance to a change in its motion. The force necessary to give a stationary pram a given acceleration is far less than the force necessary to give a stationary car the same acceleration. The resistance to a change in motion is called the inertia of an object and the amount of inertia depends on the mass of the object. Since a car has a much larger mass than a pram, the inertia of a car is much larger than that of a pram.

Newton’s second law of motion may be stated as:

The acceleration of an object acted upon by an external force is pro- portional to the force and is in the same direction as the force Thus, force ˛ acceleration, or force D a constant ð acceleration, this constant of proportionality being the mass of the object, i.e.

force = mass × acceleration

The unit of force is the newton (N) and is defined in terms of mass and acceleration. One newton is the force required to give a mass of 1 kilogram an acceleration of 1 metre per second squared. Thus

F = ma

where F is the force in newtons (N), m is the mass in kilograms (kg) and a is the acceleration in metres per second squared (m/s2), i.e.

It follows that 1 m/s2 D 1 N/kg. Hence a gravitational acceleration of 9.8 m/s2 is the same as a gravitational field of 9.8 N/kg

Newton’s third law of motion may be stated as:

For every force, there is an equal and opposite reacting force

Thus, an object on, say, a table, exerts a downward force on the table and the table exerts an equal upward force on the object, known as a reaction force or just a reaction.

For example, to calculate the force needed to accelerate a boat of mass 20 tonne uniformly from rest to a speed of 21.6 km/h in 10 minutes:

In another example, if the moving head of a machine tool requires a force of 1.2 N to bring it to rest in 0.8 s from a cutting speed of 30 m/min, then from Newton’s second law, F D ma, from which, the mass of the moving head,

The law of motion v D u C at can be used to find acceleration a, where

Centripetal Acceleration

When an object moves in a circular path at constant speed, its direction of motion is continually changing and hence its velocity (which depends on both magnitude and direction) is also continually changing. Since acceleration is the (change in velocity)/(time taken) the object has an acceleration.

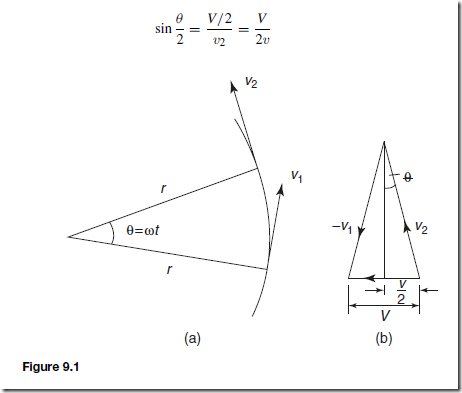
Let the object be moving with a constant angular velocity of ω and a tangential velocity of magnitude v and let the change of velocity for a small change of angle of ˛ˇD ωt) be V (see Figure 9.1(a)). Then, v2 – v1 D V.

The vector diagram is shown in Figure 9.1(b) and since the magnitudes of v1 and v2 are the same, i.e. v, the vector diagram is also an isosceles triangle.

Bisecting the angle between v2 and v1 gives:

That is, the acceleration a is  and is towards the centre of the circle of  motion (along V). It is called the centripetal acceleration. If the mass of the rotating object is m, then by Newton’s second law, the centripetal force is, and its direction is towards the centre of the circle of motion.

For example, if a vehicle of mass 750 kg travels round a bend of radius

Centre of Gravity

The centre of gravity of an object is a point where the resultant gravitational force acting on the body may be taken to act. For objects of uniform thickness lying in a horizontal plane, the centre of gravity is vertically in line with the point of balance of the object. For a thin uniform rod the point of balance and hence the centre of gravity is halfway along the rod as shown in Figure 10.1(a).

A thin flat sheet of a material of uniform thickness is called a lamina and the centre of gravity of a rectangular lamina lies at the point of intersection of its diagonals, as shown in Figure 10.1(b). The centre of gravity of a circular lamina is at the centre of the circle, as shown in Figure 10.1(c).

Equilibrium

An object is in equilibrium when the forces acting on the object are such that there is no tendency for the object to move. The state of equilibrium of an object can be divided into three groups.

(i) If an object is in stable equilibrium and it is slightly disturbed by pushing or pulling (i.e. a disturbing force is applied), the centre of gravity is raised and when the disturbing force is removed, the object returns to its original position. Thus a ball bearing in a hemispherical cup is in stable equilibrium, as shown in Figure 10.2(a).

(ii) An object is in unstable equilibrium if, when a disturbing force is applied, the centre of gravity is lowered and the object moves away from its original position. Thus, a ball bearing balanced on top of a hemispherical cup is in unstable equilibrium, as shown in Figure 10.2(b).

(iii) When an object in neutral equilibrium has a disturbing force applied, the centre of gravity remains at the same height and the object does not move when the disturbing force is removed. Thus, a ball bearing on a flat horizontal surface is in neutral equilibrium, as shown in Figure 10.2(c).

Centre of Gravity

The centre of gravity of an object is a point where the resultant gravitational force acting on the body may be taken to act. For objects of uniform thickness lying in a horizontal plane, the centre of gravity is vertically in line with the point of balance of the object. For a thin uniform rod the point of balance and hence the centre of gravity is halfway along the rod as shown in Figure 10.1(a).

A thin flat sheet of a material of uniform thickness is called a lamina and the centre of gravity of a rectangular lamina lies at the point of intersection of its diagonals, as shown in Figure 10.1(b). The centre of gravity of a circular lamina is at the centre of the circle, as shown in Figure 10.1(c).

Equilibrium

An object is in equilibrium when the forces acting on the object are such that there is no tendency for the object to move. The state of equilibrium of an object can be divided into three groups.

(i) If an object is in stable equilibrium and it is slightly disturbed by pushing or pulling (i.e. a disturbing force is applied), the centre of gravity is raised and when the disturbing force is removed, the object returns to its original position. Thus a ball bearing in a hemispherical cup is in stable equilibrium, as shown in Figure 10.2(a).

(ii) An object is in unstable equilibrium if, when a disturbing force is applied, the centre of gravity is lowered and the object moves away from its original position. Thus, a ball bearing balanced on top of a hemispherical cup is in unstable equilibrium, as shown in Figure 10.2(b).

(iii) When an object in neutral equilibrium has a disturbing force applied, the centre of gravity remains at the same height and the object does not move when the disturbing force is removed. Thus, a ball bearing on a flat horizontal surface is in neutral equilibrium, as shown in Figure 10.2(c).

Speed and Velocity

Speed

Speed is the rate of covering distance and is given by:

The usual units for speed are metres per second, (m/s or m sÐ1), or kilometres per hour, (km/h or km hÐ1 ). Thus if a person walks 5 kilometres in 1 hour, the speed of the person is 5 , that is, 5 kilometres per hour.

The symbol for the SI unit of speed (and velocity) is written as m sÐ1 , called the ‘index notation’. However, engineers usually use the symbol m/s, called the ‘oblique notation’, and it is this notation that is largely used in this chapter and other chapters on mechanics. One of the exceptions is when labelling the axes of graphs, when two obliques occur, and in this case the index notation is used. Thus for speed or velocity, the axis markings are speed/m sÐ1 or velocity/m s^-1.

For example, if a man walks 600 metres in 5 minutes

Distance/time Graph

One way of giving data on the motion of an object is graphically. A graph of distance travelled (the scale on the vertical axis of the graph) against time (the scale on the horizontal axis of the graph) is called a distance/time graph. Thus if an aeroplane travels 500 kilometres in its first hour of flight and 750 kilometres in its second hour of flight, then after 2 hours, the total distance travelled is (500 C 750) kilometres, that is, 1250 kilometres. The distance/time graph for this flight is shown in Figure 7.1.

The average speed is given by:

for any two points on line OA.

For point A, the change in distance is AX, that is, 1250 kilometres, and the change in time is OX, that is, 2 hours. Hence the average speed is , i.e. 625 kilometres per hour.

Alternatively, for point B on line OA, the change in distance is BY, that is, 625 kilometres, and the change in time is OY, that is 1 hour, hence the average speed is  , i.e. 625 kilometres per hour.

In general, the slope of line, say, MN on the distance/time graph gives the average speed of an object travelling between points M and N.

Speed/time Graph

If a graph is plotted of speed against time, the area under the graph gives the distance travelled. Thus the distance covered by the object when moving from 0 to B in Figure 7.2, is given by the area beneath the speed/time graph, shown shaded.

Velocity

The velocity of an object is the speed of the object in a specified direction. Thus, if a plane is flying due south at 500 kilometres per hour, its speed is 500 kilometres per hour, but its velocity is 500 kilometres per hour due south. It follows that if the plane had flown in a circular path for one hour at a speed of 500 kilometres per hour, so that one hour after taking off it is again over the airport, its average velocity in the first hour of flight is zero.

The average velocity is given by

If a plane flies from place O to place A, a distance of 300 kilometres in one hour, A being due north of O, then OA in Figure 7.3 represents the first

hour of flight. It then flies from A to B, a distance of 400 kilometres during the second hour of flight, B being due east of A, thus AB in Figure 7.3 represents its second hour of flight.

Its average velocity for the two hour flight is:

A graph of velocity (scale on the vertical axis) against time (scale on the horizontal axis) is called a velocity/time graph. The graph shown in Figure 7.4 represents a plane flying for 3 hours at a constant speed of 600 kilometres per hour in a specified direction. The shaded area represents velocity (vertically)

multiplied by time (horizontally), and has units of

kilometres, and represents the distance travelled in a specific direction. In this

Another method of determining the distance travelled is from:

distance travelled = average velocity × time

Thus if a plane travels due south at 600 kilometres per hour for 20 minutes, the distance covered is

Speed and Velocity

Speed

Speed is the rate of covering distance and is given by:

The usual units for speed are metres per second, (m/s or m sÐ1), or kilometres per hour, (km/h or km hÐ1 ). Thus if a person walks 5 kilometres in 1 hour, the speed of the person is 5 , that is, 5 kilometres per hour.

The symbol for the SI unit of speed (and velocity) is written as m sÐ1 , called the ‘index notation’. However, engineers usually use the symbol m/s, called the ‘oblique notation’, and it is this notation that is largely used in this chapter and other chapters on mechanics. One of the exceptions is when labelling the axes of graphs, when two obliques occur, and in this case the index notation is used. Thus for speed or velocity, the axis markings are speed/m sÐ1 or velocity/m s^-1.

For example, if a man walks 600 metres in 5 minutes

Distance/time Graph

One way of giving data on the motion of an object is graphically. A graph of distance travelled (the scale on the vertical axis of the graph) against time (the scale on the horizontal axis of the graph) is called a distance/time graph. Thus if an aeroplane travels 500 kilometres in its first hour of flight and 750 kilometres in its second hour of flight, then after 2 hours, the total distance travelled is (500 C 750) kilometres, that is, 1250 kilometres. The distance/time graph for this flight is shown in Figure 7.1.

The average speed is given by:

for any two points on line OA.

For point A, the change in distance is AX, that is, 1250 kilometres, and the change in time is OX, that is, 2 hours. Hence the average speed is , i.e. 625 kilometres per hour.

Alternatively, for point B on line OA, the change in distance is BY, that is, 625 kilometres, and the change in time is OY, that is 1 hour, hence the average speed is  , i.e. 625 kilometres per hour.

In general, the slope of line, say, MN on the distance/time graph gives the average speed of an object travelling between points M and N.

Speed/time Graph

If a graph is plotted of speed against time, the area under the graph gives the distance travelled. Thus the distance covered by the object when moving from 0 to B in Figure 7.2, is given by the area beneath the speed/time graph, shown shaded.

Velocity

The velocity of an object is the speed of the object in a specified direction. Thus, if a plane is flying due south at 500 kilometres per hour, its speed is 500 kilometres per hour, but its velocity is 500 kilometres per hour due south. It follows that if the plane had flown in a circular path for one hour at a speed of 500 kilometres per hour, so that one hour after taking off it is again over the airport, its average velocity in the first hour of flight is zero.

The average velocity is given by

If a plane flies from place O to place A, a distance of 300 kilometres in one hour, A being due north of O, then OA in Figure 7.3 represents the first

hour of flight. It then flies from A to B, a distance of 400 kilometres during the second hour of flight, B being due east of A, thus AB in Figure 7.3 represents its second hour of flight.

Its average velocity for the two hour flight is:

A graph of velocity (scale on the vertical axis) against time (scale on the horizontal axis) is called a velocity/time graph. The graph shown in Figure 7.4 represents a plane flying for 3 hours at a constant speed of 600 kilometres per hour in a specified direction. The shaded area represents velocity (vertically)

multiplied by time (horizontally), and has units of

kilometres, and represents the distance travelled in a specific direction. In this

Another method of determining the distance travelled is from:

distance travelled = average velocity × time

Thus if a plane travels due south at 600 kilometres per hour for 20 minutes, the distance covered is

Acceleration

Introduction to Acceleration

Acceleration is the rate of change of velocity with time. The average acceleration, a, is given by:

The usual units are metres per second squared (m/s2 or m sð2 ). If u is the initial velocity of an object in metres per second, v is the final velocity in metres per second and t is the time in seconds elapsing between the velocities of u and v, then:

Velocity/time Graph

A graph of velocity (scale on the vertical axis) against time (scale on the horizontal axis) is called a velocity/time graph, as introduced in Chapter 7. For the velocity/time graph shown in Figure 8.1, the slope of line OA is given by (AX/OX). AX is the change in velocity from an initial velocity, u, of zero to a final velocity, v, of 4 metres per second. OX is the time taken for this

change in velocity, thus

In general, the slope of a line on a velocity/time graph gives the acceleration. The words ‘velocity’ and ‘speed’ are commonly interchanged in everyday language. Acceleration is a vector quantity and is correctly defined as the rate of change of velocity with respect to time. However, acceleration is also the rate of change of speed with respect to time in a certain specified direction.

Free-fall and Equation of Motion

If a dense object such as a stone is dropped from a height, called free-fall, it has a constant acceleration of approximately 9.8 m/s2. In a vacuum, all objects have this same constant acceleration, vertically downwards, that is, a feather has the same acceleration as a stone. However, if free-fall takes place in air, dense objects have the constant acceleration of 9.8 m/s2 over short distances, but objects that have a low density, such as feathers, have little or no acceleration.

For bodies moving with a constant acceleration, the average acceleration is the constant value of the acceleration, and since from earlier:

For example, if a stone is dropped from an aeroplane the stone is free falling and thus has an acceleration, a, of approximately 9.8 m/s2 (taking downward motion as positive). The initial downward velocity of the stone, u, is zero. The velocity v after 2s is given by: v D u C at D 0 C 9.8 ð 2 D 19.6 m/s, i.e. the velocity of the stone after 2 s is approximately 19.6 m/s.

Acceleration

Introduction to Acceleration

Acceleration is the rate of change of velocity with time. The average acceleration, a, is given by:

The usual units are metres per second squared (m/s2 or m sð2 ). If u is the initial velocity of an object in metres per second, v is the final velocity in metres per second and t is the time in seconds elapsing between the velocities of u and v, then:

Velocity/time Graph

A graph of velocity (scale on the vertical axis) against time (scale on the horizontal axis) is called a velocity/time graph, as introduced in Chapter 7. For the velocity/time graph shown in Figure 8.1, the slope of line OA is given by (AX/OX). AX is the change in velocity from an initial velocity, u, of zero to a final velocity, v, of 4 metres per second. OX is the time taken for this

change in velocity, thus

In general, the slope of a line on a velocity/time graph gives the acceleration. The words ‘velocity’ and ‘speed’ are commonly interchanged in everyday language. Acceleration is a vector quantity and is correctly defined as the rate of change of velocity with respect to time. However, acceleration is also the rate of change of speed with respect to time in a certain specified direction.

Free-fall and Equation of Motion

If a dense object such as a stone is dropped from a height, called free-fall, it has a constant acceleration of approximately 9.8 m/s2. In a vacuum, all objects have this same constant acceleration, vertically downwards, that is, a feather has the same acceleration as a stone. However, if free-fall takes place in air, dense objects have the constant acceleration of 9.8 m/s2 over short distances, but objects that have a low density, such as feathers, have little or no acceleration.

For bodies moving with a constant acceleration, the average acceleration is the constant value of the acceleration, and since from earlier:

For example, if a stone is dropped from an aeroplane the stone is free falling and thus has an acceleration, a, of approximately 9.8 m/s2 (taking downward motion as positive). The initial downward velocity of the stone, u, is zero. The velocity v after 2s is given by: v D u C at D 0 C 9.8 ð 2 D 19.6 m/s, i.e. the velocity of the stone after 2 s is approximately 19.6 m/s.

Chemical Reactions

Introduction

A chemical reaction is an interaction between substances in which atoms are rearranged. A new substance is always produced in a chemical reaction.

Air is a mixture, and its composition by volume is approximately: nitrogen 78%, oxygen 21%, other gases (including carbon dioxide) 1%.

Oxygen

Oxygen is an odourless, colourless and tasteless element. It is slightly soluble in water (which is essential for fish), has a boiling point of Ð183° C (i.e. 90 K), a freezing point of Ð219° C (i.e. 54 K) and has approximately the same density as air. Oxygen is a strongly active chemical element and combines with many substances when they are heated.

Uses of oxygen include: chemical processing, metal cutting and welding processes to give a very hot flame when burnt with other gases, and for divers, mountaineers, fire-fighters using breathing apparatus and for medical use in hospitals.

If a substance, such as powdered copper, of known mass, is heated in air, allowed to cool, and its mass remeasured, it is found that the substance has gained in mass. This is because the copper has absorbed oxygen from the air and changed into copper oxide. In addition, the proportion of oxygen in the air passed over the copper will decrease by the same amount as the gain in mass by the copper.

All substances require the presence of oxygen for burning to take place. Any substance burning in air will combine with the oxygen. This process is

called combustion, and is an example of a chemical reaction between the burning substance and the oxygen in the air, the reaction producing heat. The chemical reaction is called oxidation.

An element reacting with oxygen produces a compound that contains only atoms of the original element and atoms of oxygen. Such compounds are called oxides. Examples of oxides include: copper oxide CuO, hydrogen oxide H2O (i.e. water) and carbon dioxide CO2

Rusting

Rusting of iron (and iron-based materials) is due to the formation on its surface of hydrated oxide of iron produced by a chemical reaction. Rusting of iron always requires the presence of oxygen and water.

Any iron or steel structure exposed to moisture is susceptible to rusting. This process, which cannot be reversed, can be dangerous since structures may be weakened by it. Examples of damage caused by rusting may be found in steel parts of a motor vehicle, the hull of ships, iron guttering, bridges and similar structures. Rusting may be prevented by:

(i) painting with water-resistant paint

(ii) galvanising the iron

(iii) plating the iron (see chapter 42, page 218)

(iv) an oil or grease film on the surface

Chemical Equations

To represent a reaction a chemical shorthand is used. A symbol represents an element (such as H for hydrogen, O for oxygen, Cu for copper, Zn for zinc, and so on) and a formula represents a compound and gives the type and number of elements in the compound. For example, one molecule of sulphuric acid, H2SO4, contains 2 atoms of hydrogen, 1 atom of sulphur and 4 atoms of oxygen. Similarly, a molecule of methane gas, CH4 , contains 1 atom of carbon and 4 atoms of hydrogen.

The rearrangement of atoms in a chemical reaction is shown by chemical equations using formulae and symbols.

For example:

In a chemical equation:

(i) each element must have the same total number of atoms on each side of the equation; for example, in chemical equation (b) above each side of the equation has 1 zinc atom, 2 hydrogen atoms, 1 sulphur atom and 4 oxygen atoms

(ii) a number written in front of a molecule multiplies all the atoms in that molecule

Acids and Alkalis

An acid is a compound containing hydrogen in which the hydrogen can be easily replaced by a metal. For example, in equation (b) above, it is shown that zinc reacts with sulphuric acid to give zinc sulphate and hydrogen.

An acid produces hydrogen ions HC in solution (an ion being a charged particle formed when atoms or molecules lose or gain electrons). Examples of acids include: sulphuric acid, H2SO4 , hydrochloric acid, HCl and nitric acid HNO3

A base is a substance that can neutralise an acid (i.e. remove the acidic properties of acids). An alkali is a soluble base. When in solution an alkali produces hydroxyl ions, OHÐ . Examples of alkalis include: sodium hydroxide, NaOH (i.e. caustic soda), calcium hydroxide, Ca(OH)2, ammonium hydroxide, NH4OH and potassium hydroxide, KOH (i.e. caustic potash).

A salt is the product of the neutralisation between an acid and a base, i.e.

Examples of salts include: sodium chloride, NaCl (i.e. common salt), potassium sulphate, K2SO4 , copper sulphate, CuSO4 and calcium carbonate, CaCO3 (i.e. limestone).

An indicator is a chemical substance, which when added to a solution, indicates the acidity or alkalinity of the solution by changing colour. Litmus is a simple two-colour indicator which turns red in the presence of acids and blue in the presence of alkalis. Two other examples of indicators are ethyl orange (red for acids, yellow for alkalis) and phenolphthalein (colourless for acids, pink for alkalis).

The pH scale (pH meaning ‘the potency of hydrogen’) represents, on a scale from 0 to 14, degrees of acidity and alkalinity. 0 is strongly acidic, 7 is neutral and 14 is strongly alkaline. Some average pH values include:

concentrated hydrochloric acid, HCl 1.0, lemon juice 3.0, milk 6.6, pure water 7.0, sea water 8.2, concentrated sodium hydroxide, NaOH 13.0

Acids have the following properties:

(i) Almost all acids react with carbonates and bicarbonates, (a carbonate being a compound containing carbon and oxygen — an example being sodium carbonate, i.e. washing soda)

(ii) Dilute acids have a sour taste; examples include citric acid (lemons), acetic acid (vinegar) and lactic acid (sour milk).

(iii) Acid solutions turn litmus paper red, methyl orange red and phenolph- thalein colourless, as mentioned above.

(iv) Most acids react with higher elements in the electrochemical series (see chapter 42) and hydrogen is released.

Alkalis have the following properties:

(i) Alkalis neutralise acids to form a salt and water only.

(ii) Alkalis have little effect on metals.

(iii) Alkalis turn litmus paper blue, methyl orange yellow and phenolphthalein pink, as mentioned above.

(iv) Alkalis are slippery when handled; strong alkalis are good solvents for certain oils and greases.

 Standard Quantity Symbols and their Units

Chemical Reactions

Introduction

A chemical reaction is an interaction between substances in which atoms are rearranged. A new substance is always produced in a chemical reaction.

Air is a mixture, and its composition by volume is approximately: nitrogen 78%, oxygen 21%, other gases (including carbon dioxide) 1%.

Oxygen

Oxygen is an odourless, colourless and tasteless element. It is slightly soluble in water (which is essential for fish), has a boiling point of Ð183° C (i.e. 90 K), a freezing point of Ð219° C (i.e. 54 K) and has approximately the same density as air. Oxygen is a strongly active chemical element and combines with many substances when they are heated.

Uses of oxygen include: chemical processing, metal cutting and welding processes to give a very hot flame when burnt with other gases, and for divers, mountaineers, fire-fighters using breathing apparatus and for medical use in hospitals.

If a substance, such as powdered copper, of known mass, is heated in air, allowed to cool, and its mass remeasured, it is found that the substance has gained in mass. This is because the copper has absorbed oxygen from the air and changed into copper oxide. In addition, the proportion of oxygen in the air passed over the copper will decrease by the same amount as the gain in mass by the copper.

All substances require the presence of oxygen for burning to take place. Any substance burning in air will combine with the oxygen. This process is

called combustion, and is an example of a chemical reaction between the burning substance and the oxygen in the air, the reaction producing heat. The chemical reaction is called oxidation.

An element reacting with oxygen produces a compound that contains only atoms of the original element and atoms of oxygen. Such compounds are called oxides. Examples of oxides include: copper oxide CuO, hydrogen oxide H2O (i.e. water) and carbon dioxide CO2

Rusting

Rusting of iron (and iron-based materials) is due to the formation on its surface of hydrated oxide of iron produced by a chemical reaction. Rusting of iron always requires the presence of oxygen and water.

Any iron or steel structure exposed to moisture is susceptible to rusting. This process, which cannot be reversed, can be dangerous since structures may be weakened by it. Examples of damage caused by rusting may be found in steel parts of a motor vehicle, the hull of ships, iron guttering, bridges and similar structures. Rusting may be prevented by:

(i) painting with water-resistant paint

(ii) galvanising the iron

(iii) plating the iron (see chapter 42, page 218)

(iv) an oil or grease film on the surface

Chemical Equations

To represent a reaction a chemical shorthand is used. A symbol represents an element (such as H for hydrogen, O for oxygen, Cu for copper, Zn for zinc, and so on) and a formula represents a compound and gives the type and number of elements in the compound. For example, one molecule of sulphuric acid, H2SO4, contains 2 atoms of hydrogen, 1 atom of sulphur and 4 atoms of oxygen. Similarly, a molecule of methane gas, CH4 , contains 1 atom of carbon and 4 atoms of hydrogen.

The rearrangement of atoms in a chemical reaction is shown by chemical equations using formulae and symbols.

For example:

In a chemical equation:

(i) each element must have the same total number of atoms on each side of the equation; for example, in chemical equation (b) above each side of the equation has 1 zinc atom, 2 hydrogen atoms, 1 sulphur atom and 4 oxygen atoms

(ii) a number written in front of a molecule multiplies all the atoms in that molecule

Acids and Alkalis

An acid is a compound containing hydrogen in which the hydrogen can be easily replaced by a metal. For example, in equation (b) above, it is shown that zinc reacts with sulphuric acid to give zinc sulphate and hydrogen.

An acid produces hydrogen ions HC in solution (an ion being a charged particle formed when atoms or molecules lose or gain electrons). Examples of acids include: sulphuric acid, H2SO4 , hydrochloric acid, HCl and nitric acid HNO3

A base is a substance that can neutralise an acid (i.e. remove the acidic properties of acids). An alkali is a soluble base. When in solution an alkali produces hydroxyl ions, OHÐ . Examples of alkalis include: sodium hydroxide, NaOH (i.e. caustic soda), calcium hydroxide, Ca(OH)2, ammonium hydroxide, NH4OH and potassium hydroxide, KOH (i.e. caustic potash).

A salt is the product of the neutralisation between an acid and a base, i.e.

Examples of salts include: sodium chloride, NaCl (i.e. common salt), potassium sulphate, K2SO4 , copper sulphate, CuSO4 and calcium carbonate, CaCO3 (i.e. limestone).

An indicator is a chemical substance, which when added to a solution, indicates the acidity or alkalinity of the solution by changing colour. Litmus is a simple two-colour indicator which turns red in the presence of acids and blue in the presence of alkalis. Two other examples of indicators are ethyl orange (red for acids, yellow for alkalis) and phenolphthalein (colourless for acids, pink for alkalis).

The pH scale (pH meaning ‘the potency of hydrogen’) represents, on a scale from 0 to 14, degrees of acidity and alkalinity. 0 is strongly acidic, 7 is neutral and 14 is strongly alkaline. Some average pH values include:

concentrated hydrochloric acid, HCl 1.0, lemon juice 3.0, milk 6.6, pure water 7.0, sea water 8.2, concentrated sodium hydroxide, NaOH 13.0

Acids have the following properties:

(i) Almost all acids react with carbonates and bicarbonates, (a carbonate being a compound containing carbon and oxygen — an example being sodium carbonate, i.e. washing soda)

(ii) Dilute acids have a sour taste; examples include citric acid (lemons), acetic acid (vinegar) and lactic acid (sour milk).

(iii) Acid solutions turn litmus paper red, methyl orange red and phenolph- thalein colourless, as mentioned above.

(iv) Most acids react with higher elements in the electrochemical series (see chapter 42) and hydrogen is released.

Alkalis have the following properties:

(i) Alkalis neutralise acids to form a salt and water only.

(ii) Alkalis have little effect on metals.

(iii) Alkalis turn litmus paper blue, methyl orange yellow and phenolphthalein pink, as mentioned above.

(iv) Alkalis are slippery when handled; strong alkalis are good solvents for certain oils and greases.

 Standard Quantity Symbols and their Units

Elements

There are a very large number of different substances in existence, each sub- stance containing one or more of a number of basic materials called elements. ‘An element is a substance which cannot be separated into anything simpler by chemical means’. There are 92 naturally occurring elements and 13 others, which have been artificially produced.

Some examples of common elements with their symbols are: Hydrogen H, Helium He, Carbon C, Nitrogen N, Oxygen O, Sodium Na, Magnesium Mg, Aluminium Al, Silicon Si, Phosphorus P, Sulphur S, Potassium K, Calcium Ca, Iron Fe, Nickel Ni, Copper Cu, Zinc Zn, Silver Ag, Tin Sn, Gold Au, Mercury Hg, Lead Pb and Uranium U.

Atoms

Elements are made up of very small parts called atoms. ‘An atom is the smallest part of an element which can take part in a chemical change and which retains the properties of the element’.

Each of the elements has a unique type of atom.

In atomic theory, a model of an atom can be regarded as a miniature solar system. It consists of a central nucleus around which negatively charged particles called electrons orbit in certain fixed bands called shells. The nucleus contains positively charged particles called protons and particles having no electrical charge called neutrons.

An electron has a very small mass compared with protons and neutrons. An atom is electrically neutral, containing the same number of protons as electrons. The number of protons in an atom is called the atomic number of the element of which the atom is part. The arrangement of the elements in order of their atomic number is known as the periodic table.

The simplest atom is hydrogen, which has 1 electron orbiting the nucleus and 1 proton in the nucleus. The atomic number of hydrogen is thus 1. The hydrogen atom is shown diagrammatically in Figure 4.1(a). Helium has 2 electrons orbiting the nucleus, both of then occupying the same shell at the same distance from the nucleus, as shown in Figure 4.1(b).

The first shell of an atom can have up to 2 electrons only, the second shell can have up to 8 electrons only and the third shell up to 18 electrons only. Thus an aluminium atom which has 13 electrons orbiting the nucleus is arranged as shown in Figure 1(c).

Molecules

When elements combine together, the atoms join to form a basic unit of new substance. This independent group of atoms bonded together is called a molecule. ‘A molecule is the smallest part of a substance which can have a separate stable existence’.

All molecules of the same substance are identical. Atoms and molecules are the basic building blocks from which matter is constructed.

Compounds

When elements combine chemically their atoms interlink to form molecules of a new substance called a compound. ‘A compound is a new substance containing two or more elements chemically combined so that their properties are changed’.

For example, the elements hydrogen and oxygen are quite unlike water, which is the compound they produce when chemically combined.

The components of a compound are in fixed proportion and are difficult to separate. Examples include:

(i) water H2O, where 1 molecule is formed by 2 hydrogen atoms combining with 1 oxygen atom,

(ii) carbon dioxide CO2 , where 1 molecule is formed by 1 carbon atom combining with 2 oxygen atoms,

(iii) sodium chloride NaCl (common salt), where 1 molecule is formed by 1 sodium atom combining with 1 chlorine atom, and

(iv) copper sulphate CuSO4 , where 1 molecule is formed by 1 copper atom, 1 sulphur atom and 4 oxygen atoms combining.

Mixtures

‘A mixture is a combination of substances which are not chemically joined together’. Mixtures have the same properties as their components. Also, the components of a mixture have no fixed proportion and are easy to separate. Examples include:

(i) oil and water

(ii) sugar and salt

(iii) air, which is a mixture of oxygen, nitrogen, carbon dioxide and other gases

(iv) iron and sulphur

(v) sand and water

Mortar is an example of a mixture — consisting of lime, sand and water.

Compounds can be distinguished from mixtures in the following ways:

(i) The properties of a compound are different to its constituent components whereas a mixture has the same properties as it constituent components.

(ii) The components of a compound are in fixed proportion whereas the components of a mixture have no fixed proportion.

(iii) The atoms of a compound are joined, whereas the atoms of a mixture are

free.

(iv) When a compound is formed, heat energy is produced or absorbed whereas when a mixture is formed little or no heat is produced or absorbed.

Solutions

‘A solution is a mixture in which other substances are dissolved’.

A solution is a mixture from which the two constituents may not be separated by leaving it to stand, or by filtration. For example, sugar dissolves in tea, salt dissolves in water and copper sulphate crystals dissolve in water leaving it a clear blue colour. The substance that is dissolved, which may be solid, liquid or gas, is called the solute, and the liquid in which it dissolves is called the solvent. Hence solvent Y solute = solution.

A solution has a clear appearance and remains unchanged with time.

Suspensions

‘A suspension is a mixture of a liquid and particles of a solid which do not dissolve in the liquid’.

The solid may be separated from the liquid by leaving the suspension to stand, or by filtration. Examples include:

(i) sand in water

(ii) chalk in water

(iii) petrol and water

Solubility

If a material dissolves in a liquid the material is said to be soluble. For example, sugar and salt are both soluble in water.

If, at a particular temperature, sugar is continually added to water and the mixture stirred there comes a point when no more sugar can dissolve. Such a solution is called saturated. ‘A solution is saturated if no more solute can be made to dissolve, with the temperature remaining constant’.

‘Solubility is a measure of the maximum amount of a solute which can be dissolved in 0.1 kg of a solvent, at a given temperature’. For example, the solubility of potassium chloride at 20°C is 34 g per 0.1 kg of water, or, its percentage solubility is 34%

(i) Solubility is dependent on temperature. When solids dissolve in liquids, as the temperature is increased, in most cases the amount of solid that will go into solution also increases. (More sugar is dissolved in a cup of hot tea than in the same amount of cold water.) There are exceptions to this, for the solubility of common salt in water remains almost constant and the solubility of calcium hydroxide decreases as the temperature increases.

(ii) Solubility is obtained more quickly when small particles of a substance are added to a liquid than when the same amount is added in large particles. For example, sugar lumps take longer to dissolve in tea than does granulated sugar.

(iii) A solid dissolves in a liquid more quickly if the mixture is stirred or shaken, i.e. solubility depends on the speed of agitation.

Crystals

A crystal is a regular, orderly arrangement of atoms or molecules forming a distinct pattern, i.e. an orderly packing of basic building blocks of matter. Most solids are crystalline in form and these include crystals such as common salt and sugar as well as the metals. Substances that are non-crystalline, are called amorphous, examples including glass and wood. Crystallisation is the process of isolating solids from solution in a crystalline form. This may be carried out by adding a solute to a solvent until saturation is reached, raising the temperature, adding more solute and repeating the process until a fairly strong solution is obtained, and then allowing the solution to cool, when crystals will separate. There are several examples of crystalline form that occur naturally, examples including graphite, quartz, diamond and common salt.

Crystals can vary in size but always have a regular geometric shape with flat faces, straight edges and having specific angles between the sides. Two common shapes of crystals are shown in Figure 4.2. The angles between the faces of the common salt crystal (Figure 4.2(a)) are always 90° and those of a quartz crystal (Figure 2(b)) are always 60° . A particular material always produces exactly the same shape of crystal.

Figure 4.3 shows a crystal lattice of sodium chloride. This is always a cubic shaped crystal being made up of 4 sodium atoms and 4 chlorine atoms. The sodium chloride crystals then join together as shown.

Metals

Metals are polycrystalline substances. This means that they are made up of a large number of crystals joined at the boundaries, the greater the number of boundaries the stronger the material.

Every metal, in the solid state, has its own crystal structure. To form an alloy, different metals are mixed when molten, since in the molten state they do not have a crystal lattice. The molten solution is then left to cool and solidify. The solid formed is a mixture of different crystals and an alloy is thus referred to as a solid solution. Examples include:

(i) brass, which is a combination of copper and zinc,

(ii) steel, which is mainly a combination of iron and carbon,

(iii) bronze, which is a combination of copper and tin.

Alloys are produced to enhance the properties of the metal, such as greater strength. For example, when a small proportion of nickel (say, 2% Ð 4%) is added to iron the strength of the material is greatly increased. By controlling the percentage of nickel added, materials having different specifications may be produced.

A metal may be hardened by heating it to a high temperature then cooling it very quickly. This produces a large number of crystals and therefore many boundaries. The greater the number of crystal boundaries, the stronger is the metal.

A metal is annealed by heating it to a high temperature and then allowing it to cool very slowly. This causes larger crystals, thus less boundaries and hence a softer metal.