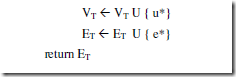Prim’s Algorithm
-to find minimum spanning tree
Some useful definitions:
• Fringe edge: An edge which has one vertex is in partially constructed tree Ti and the other is not.
• Unseen edge: An edge with both vertices not in Ti
Algorithm:
ALGORITHM Prim (G)
//Prim’s algorithm for constructing a MST
//Input: A weighted connected graph G = { V, E }
//Output: ET the set of edges composing a MST of G
// the set of tree vertices can be initialized with any vertex
Find a minimum-weight edge e* = (v*, u*) among all the edges (v, u) such that v is in VT and u is in V – VT
The method:
STEP 1: Start with a tree, T0, consisting of one vertex
STEP 2: “Grow” tree one vertex/edge at a time
• Construct a series of expanding sub-trees T1, T2, … Tn-1.
• At each stage construct Ti + 1 from Ti by adding the minimum weight edge connecting a vertex in tree (Ti) to one vertex not yet in tree, choose from “fringe” edges (this is the “greedy” step!)
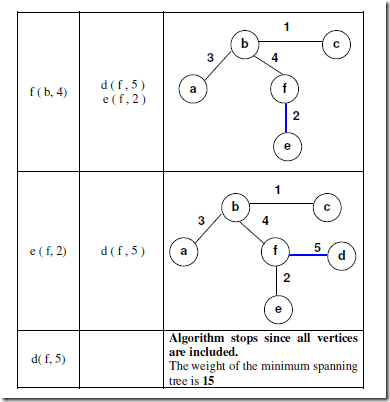
Algorithm stops when all vertices are included
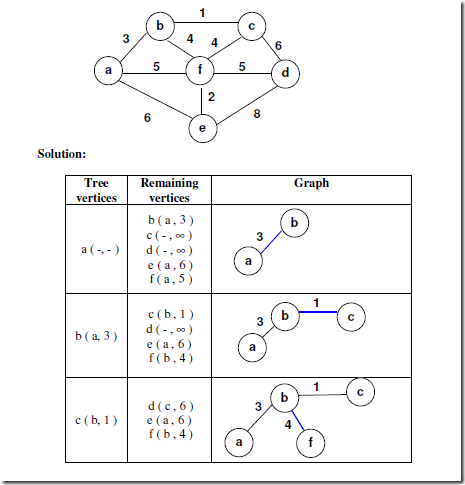
Example:
Apply Prim’s algorithm for the following graph to find MST.
Efficiency:
Efficiency of Prim’s algorithm is based on data structure used to store priority queue.
• Unordered array: Efficiency: Θ(n2)
• Binary heap: Efficiency: Θ(m log n)
• Min-heap: For graph with n nodes and m edges: Efficiency: (n + m) log n
Conclusion:
• Prim’s algorithm is a “vertex based algorithm”
• Prim’s algorithm “Needs priority queue for locating the nearest vertex.” The choice of priority queue matters in Prim implementation.
o Array – optimal for dense graphs
o Binary heap – better for sparse graphs
o Fibonacci heap – best in theory, but not in practice