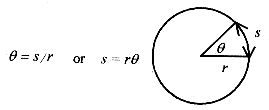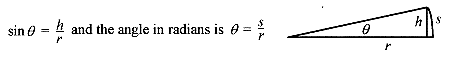Trigonometry
The trigonometric relations can be defined in terms of right angle trigonometry or through their functions. The basic trigonometric relations, as they relate to right triangles, are shown in the box.
![image_thumb[17]](http://lh5.ggpht.com/-q1AYoWdhvJA/VAXhKPpnoGI/AAAAAAAAfqU/SJPtZnVIrHY/s1600-h/image_thumb%25255B17%25255D%25255B2%25255D.png "image_thumb[17]")
Fig. I-5.
Graphs of the trigonometric relations are shown in the
![image_thumb[18]](http://lh4.ggpht.com/-foetOfx5CbI/VAXhN663d7I/AAAAAAAAfqk/ho9eKlPrKcM/s1600-h/image_thumb%25255B18%25255D%25255B2%25255D.png "image_thumb[18]")
Angles are measured in radians. Radian measure is a pure number, the ratio of are length to radius to produce the desired angle. Figure I 6 shows the relationship of are length to radius to define the angle.
The s = rè is the basic relation in rotational motion.
The relation between radians and degrees is 2ðrad = 360°
The sine of small angles can be approximated with the radian measurement of angles. Figure I 7 shows the sine of a very small angle and the radian measure of the angle. Take the two sides of the triangle as equal to r. For small angles this is nearly an isosceles triangle. The sine of the angle is
For small angles s is approximately h and the sine of the angle is nearly equal to the angle (measured in radians). Take a small angle, ð/30, which is equal to 6 degrees, and as an exercise find the sin 6° and ð/30 and verify that the error in using the radian rather than the sine is 2 parts in 1000 or 0.2%. There are a large number of trigonometric identities that can be derived using geometry and algebra. Several of the more common are in the box below.
