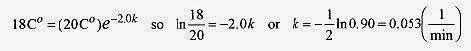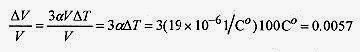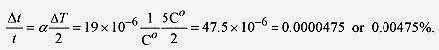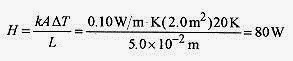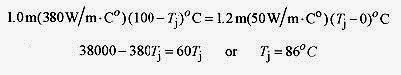Temperature and Calorimetry
Temperature and variations in temperature are measured by a variety of physical properties: volume of a liquid, length of a rod, resistance of a metal, pressure of a gas at constant volume, or volume of a gas at constant pressure. Thermometric devices (thermometers) are not all linear, though some are linear over a fairly wide range, and it is necessary in selecting a thermometer to fit the linearity of the thermometer to the range of temperatures to be measured.
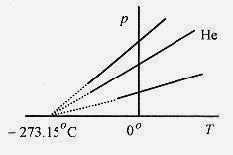
The standard in temperature measurement is the constant volume gas thermometer. An ideal gas at low density, usually helium, confined to a constant volume has a linear relation between temperature and pressure as shown in Fig. 17 1. The dotted portion of the line is an extension of the linear relationship. Gas thermometers stop being linear at low temperatures because the gas stops being a gas and becomes liquid or solid. Extrapolating the straight line relationship gives an intercept of 273.15‹C corresponding to zero pressure. Figure 17 1 shows graphs of pressure versus temperature for several different gases. These several gases show this linear relationship between pressure and temperature; and while the slopes of the lines are different, they all extrapolate to the same temperature.
Fig.17 1
The important point is that while the slopes are different, the relation between pressure and temperature is a straight line over a wide range of temperatures, and the lines all extrapolate to one specific temperature, which is taken as the absolute zero of temperature. This temperature is 0‹K (Kelvin) or 273.15‹C. (The international standard is not to use the degree symbol with the Kelvin scale. Popular practice is either way.) The reason for this rather odd number ( 273.15) is that when the zero on the Celsius scale is calibrated with the freezing point of water at standard atmospheric pressure, the absolute zero is 273.15 degree units below (this zero). The most accurate calibration point for a thermometer is the triple point of water, where the conditions of pressure and temperature are such that water, ice, and vapor all coexist at the same time.
The Kelvin and Celsius scales have the same size degree. The Fahrenheit scale uses the same end points for calibration (freezing and vapor point of water) but the scale starts at 32 and ends at 212, giving a much smaller degree. Temperature is written as 20‹C or 50‹C while temperature difference is written as 30C‹.
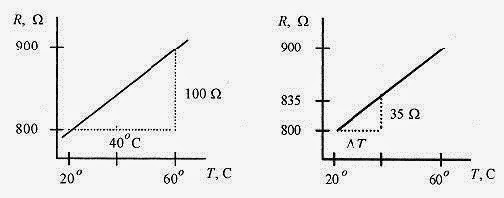
17 1 Consider a linear temperature device such as the resistance of a piece of metal. If the resistance of the device is 800ƒ¶ at 20‹C and 900ƒ¶ at 60‹C, what is the temperature when the device reads 835ƒ¶?
Fig. 17 2
Solution: Figure 17 2 shows the linear relationship of the device. Since the slope is a constant, the slope of the graph on the right is equal to the slope of the graph on the left (similar triangles).
So
or ΔT=14‹C and the measured temperature is 34‹C.
<><><><><><><><><><><><>
Hot objects placed in contact with cold objects cool and warm (respectively) according to a constant that depends on the conditions of contact and the difference in temperature. This heating or cooling is most conveniently expressed as a differential equation
In words this differential equation states that the change over time of the difference in temperature is proportional to the difference in temperature. The rate at which something cools is directly proportional to the difference in temperature with its surroundings. The negative sign is a reminder that the change in ΔT is such as to reduce ΔT. The equation is solved by separating
The constant can be evaluated by taking an initial temperature difference ΔT0. Substituting into this equation for t=0 and ΔT0 yields In ΔT0 = const and the equation reads In ΔT = In ΔT0 kt or In and switching to exponential format
This equation states that the difference in temperature between a hot body and a cold body in contact is proportional to the initial difference and a decaying exponential. This is very much what we expect from experience. Note that this equation is in the same form as other decay equations that describe, for example, the rate of radioactive decay as proportional to the amount of decaying product remaining.
17 2 Two objects have an initial temperature difference of 20C‹. In two minutes the temperature difference is 18C‹. Calculate the time for the temperature difference to be 10C‹.
Solution: This is a classic type of problem where the physical law is known, data is given to calculate the specific relationship, and this relationship is used to predict something. Keep this process in mind as you go through this problem. It is used in the solution of many problems in physics.
The basic law is ΔT=ΔT0e kt
Now, use the given data to determine k. Units are left off in the exponent to avoid clutter, but keep in mind that the 2.0 is in minutes, so k will be in reciprocal minutes.
This gives k for this specific situation, and the law for this specific situation is
Now ask, what time is required for the temperature difference to decline to 10‹C, ΔT=10‹C for an initial difference of 20‹C.
10 = 20e 0.053t and switching to logarithms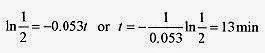
Go back over this problem and be sure you understand the procedure and how to manipulate the exponents and logarithms. Practice performing these operations on your calculator so you will be able to do them rapidly and accurately on a test
. <><><><><><><><><><><><>
Solids expand and contract with their change in length proportional to their length and change in temperature![]()
The α’s of various materials are tabulated in most physics texts.
17 3 A steel bridge is set in concrete pillars on opposite sides of a river. The bridge is 300m long, and the work is performed on a day when the temperature is 18‹C. What clearance is required for the bridge not to buckle at 45‹C? (αsteel=11~10 6/C‹)
Solution: The change in length is![]()
A minimum of 8.9cm would be required for expansion.
<><><><><><><><><><><><>
For flat objects the change in length is isotropic (the same in all directions) so that the diagonal of a plate, the diameter or circumference of a hole punched in the plate, or any length changes according to Δl=αlΔT; so that for areas
17 4 Calculate the change in volume of a brass sphere of 8.0cm in radius on going from 0‹C to 100‹C. (αbrass=19~10 6/C‹)
Solution: The change in volume is
The fractional change in volume ΔV/V is
The percentage change in volume is 0.57%.
<><><><><><><><><><><><>
Consider the effect of temperature on the period of a pendulum clock. The period of a pendulum is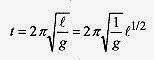
Taking the differential with respect to l, the variable that depends on temperature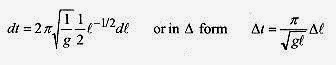
Now the Δl can be written in terms of change in temperature as Δl=αlΔT, so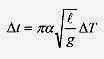
A more interesting formula is one for the fractional change in period Δt/t ![]()
17 5 Calculate the fractional change in period for a brass pendulum going through a 5C‹ change from summer to winter (not unusual).
As the temperature increases, the length of the pendulum gets longer, and the time for one oscillation gets longer. Pendulum clocks run slower in the summer.
Calorimetry
Heat is a form of energy. The unit of heat is the calorie, the heat to raise 1.0g of water from 14.5‹C to 15.5‹C. The kilocalorie or kcal is also popular. Food calories are actually kilocalories.
The British heat unit is the British Thermal Unit (BTU), the heat to raise 1.0 pound of water from 63‹F to 64‹F. The joule equivalence is 1cal=4.2J.
The quantity of heat necessary to raise the temperature of a mass of material is
where c, the specific heat, is the amount of heat per g.C‹ for the material. The specific heat for water is 1.0cal/g.C‹. Tables of specific heats are in most physics texts.
17 6 How much heat is required to raise a 1.8kg copper tea kettle containing 2.0kg of water from 20‹C to 100‹C? The specific heat of copper is 0.092cal/g.C‹.
The specific heat is sometimes expressed in J/kg.K rather than cal/g.C‹. For the previous problem the calculations would read
Use the calorie to joule equivalence to verify the numbers in this problem.
The quantity of material is sometimes given in moles, n. The total mass is related to the number of moles via m=nM where M is the mass per mole of the material. Measuring the mass in number of moles, heat capacity would be calculated with the molar heat capacity, the heat in joules per mole.C‹ or mole.K. (Remember, the Celsius and Kelvin degrees are the same size.)
The equilibrium temperature of a mixture can be determined by knowing the quantity of heat necessary to affect a change in temperature
17 7 A 150g cup of coffee (water) at 80‹C has added to it 20g of sugar (carbon) at 25‹C. What is the final temperature of the insulated mixture? (cc=0.12cal/g.C‹)
Solution: In this problem heat from the water raises the temperature of the carbon until they are both at the same temperature. Saying it simply, this is a Goesinto problem. The heat in the water Goesinto heating the carbon until they both reach an equilibrium temperature, T.
The heat leaving the water is 150g(1.0cal/g.C‹)(80 T‹C.
The final temperature is between 80 and 25, so writing the temperature difference as 80 T produces a positive number (of calories).
This heat goes to raise the temperature of the carbon 20g(0.12cal/g.C‹)(T 25)‹C.
Notice that the temperature difference in parentheses is written so as to produce a positive number.
The equation will read: The heat from the water Goesinto heating the carbon.
or
These problems can be complicated with three or more components at different temperatures. If you guess wrong as to where the equilibrium temperature lies, the calculations will produce a temperature higher or lower than the original temperatures. If this occurs you know that the initial assumption was wrong, so go back with another (better) assumption of the equilibrium temperature and do the problem over again. The main problem with calorimetry problems is keeping the algebraic signs correct. These problems can be done with a positive heat minus negative heat approach, but the Goesinto approach cuts down on the number of negative signs and reduces the possible number of places where you can get a sign wrong.
Phase Change
If water is heated from room temperature to the vapor point it takes 1 calorie of heat (energy) to raise each gram 1K degree. When the vapor point is reached a discrete amount of energy is required to convert each gram (or kilogram) of water at 100‹C to vapor without raising its temperature. This amount of energy is called the heat of vaporization and for water is 2.3~106J/kg.
A similar phenomenon is observed when a solid is taken to the liquid phase. The heat of fusion, the heat to change 1.0kg of solid (water) to liquid at 0‹C is 3.3~105J/kg. Tables of heats of fusion and vaporization are in most physics texts. Problems involving heat of fusion or heat of vaporization must be done carefully, because the energy requirements for these changes of state are very large. Converting a small amount of ice to water consumes a large amount of energy compared to raising the temperature of the water. It takes 4.2~103J per kg for each degree of temperature while it takes 3.3~105J per kg to convert ice to water with no temperature rise!
17 8 An insulated container holds 3.0kg of water at 25‹C. One kilogram of ice at 0‹C is added to the mixture. What is the final temperature and composition (ice and water) of the mixture?
Solution: First calculate the energy to bring all the water to 0‹C.
Now ask how much ice could be melted with this amount of energy.![]()
All the ice will not be melted so the final mixture will be 3.95kg of water and 0.05kg of ice all at 0‹C. There will be no further heat transfer because both the water and the ice are at the same temperature.
<><><><><><><><><><><><>
17 9 If in the previous problem the amount of ice is reduced to 0.50kg what is the final temperature of the composition?
Solution: Based on the previous calculation there is not enough ice to lower the temperature of the water to 0‹C. One way of doing the problem is to calculate the drop in temperature of the 3.0kg of water at 25‹C due to the melting ice, then treat the problem as a mixture of two amounts of water at different temperatures.
However, since we already know that all the ice melts and the final mixture is between 0‹C and 25‹C, the equation for the final temperature can be set up with the statement: The energy in the 3.0kg of water at 25‹C Goesinto melting the ice and raising the temperature of the 0‹C water.
Heat Flow
Conduction of heat or heat flow depends on the temperature difference, cross section, separation, and a constant of the material according to 
The units of H are energy per time or Joule/sec which is a watt. The thermal conductivity, k, has units of W/m.K.
17 11 Calculate the heat flow through a wooden door of area 2.0m2 and thickness 5.0cm when the temperature difference is 20K. The k for wood is 0.10W/m.K.
<><><><><><><><><><><><>
17 11 Two rods with cross sections of 4.0cm2, one copper of 1.2m length, and the other steel of 1.0m length, are connected together with their opposite ends held at 100‹C and 0‹C as shown. What is the heat flow and the temperature of the junction at equilibrium?kcu=380W/m.C‹ and kst=50W/m.C‹)
Solution: The key to this problem is that the heat flow in the two rods must be the same. If the heat flow in the copper is greater than the heat flow in the steel then the joint will get hot. This does not happen so the heat flow must be the same. 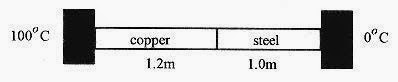
Fig.17 3
Take the temperature of the junction as Tj, and set the heat flows equal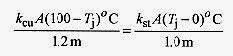
The heat flow is from either formula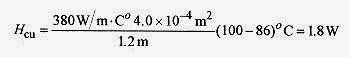
Calorimetry combined with other energy analysis techniques can be used to solve other types of problems.
17 12 A block of ice initially at 50kg and traveling at 5.4m/s slides along a horizontal surface until it comes to rest. Assume all the heat generated due to friction is used to melt the ice. How much ice is melted?
Solution: All the kinetic energy in the block Goesinto work expended to overcome friction, and all this energy Goesinto melting the ice. The initial kinetic energy is ![]()
All this energy is used to melt the ice. ![]() <><><><><><><><><><><><>
<><><><><><><><><><><><>
17 13 A 5.0kg bullet traveling 800m/s passes through a 5.0kg copper block at rest on a frictionless table. Twenty percent of the kinetic energy of the bullet goes into heating the block. Thirty percent goes into kinetic energy of the block. Fifty percent remains with the bullet. The block and bullet are initially at 25‹C. What is the temperature and speed of the block and the speed of the bullet? (ccu=390J/kg.C‹)
Solution: First find the initial kinetic energy of the bullet. ![]()
Twenty percent of this, or 320J, goes to heating the copper block. ![]()
Thirty percent, or 480J, goes to kinetic energy of the block.![]()
Fifty percent, or 800J, stays with the bullet.