Electric Fields, Capacitance and Permittivity
Any region in which an electric charge experiences a force is called an electrostatic field. Electric fields, Coulombs law, capacitance and permittivity are discussed in chapter 44 — refer back to page 233. Summarising the main formulae:
Polarisation
When a dielectric is placed between charged plates, the capacitance of the system increases. The mechanism by which a dielectric increases capacitance is called polarisation. In an electric field the electrons and atomic nuclei of the dielectric material experience forces in opposite directions. Since the electrons in an insulator cannot flow, each atom becomes a tiny dipole (i.e. an arrangement of two electric charges of opposite polarity) with positive and negative charges slightly separated, i.e. the material becomes polarised.
Within the material this produces no discernible effects. However, on the surfaces of the dielectric, layers of charge appear. Electrons are drawn towards the positive potential, producing a negative charge layer, and away from the negative potential, leaving positive surface charge behind. Therefore the dielectric becomes a volume of neutral insulator with surface charges of opposite polarity on opposite surfaces. The result of this is that the electric field inside the dielectric is less than the electric field causing the polarisation, because these two charge layers give rise to a field, which opposes the electric field causing it. Since electric field strength,
the p.d. between the plates, V = Ed. Thus, if E decreases when the dielectric is inserted, then V falls too and this drop in p.d. occurs without change of charge on the plates.
Thus, since capacitance 
, capacitance increases, this increase being by a factor equal to εr above that obtained with a vacuum dielectric.
There are two main ways in which polarisation takes place:
(i) The electric field, as explained above, pulls the electrons and nucleii in opposite directions because they have opposite charges, which makes each atom into an electric dipole. The movement is only small and takes place very fast since the electrons are very light. Thus, if the applied electric field is varied periodically, the polarisation, and hence the permittivity due to these induced dipoles, is independent of the frequency of the applied field.
(ii) Some atoms have a permanent electric dipole as a result of their structure and, when an electric field is applied, they turn and tend to align along the field. The response of the permanent dipoles is slower than the response of the induced dipoles and that part of the relative permittivity which arises from this type of polarisation decreases with increase of frequency.
Most materials contain both induced and permanent dipoles, so the relative permittivity usually tends to decrease with increase of frequency.
Dielectric Strength
The maximum amount of field strength that a dielectric can withstand is called the dielectric strength of the material. When an electric field is established across the faces of a material, molecular alignment and distortion of the electron orbits around the atoms of the dielectric occur. This produces a mechanical stress, which in turn generates heat. The production of heat represents a dissipation of power, such a loss being present in all practical dielectrics, especially when used in high-frequency systems where the field polarity is continually and rapidly changing.
A dielectric whose conductivity is not zero between the plates of a capacitor provides a conducting path along which charges can flow and thus dischargethe capacitor. The resistance R of the dielectric is given by:
the thickness of the dielectric film (which may be as small as 0.001 mm) and a being the area of the capacitor plates. The resistance R of the dielectric may be represented as a leakage resistance across an ideal capacitor (see dielectric loss later). The required lower limit for acceptable resistance between the plates varies with the use to which the capacitor is put. High-quality capacitors have high shunt-resistance values. A measure of dielectric quality is the time taken for a capacitor to discharge a given amount through the resistance of the dielectric. This is related to the product CR.
is a characteristic of a given dielectric. In practice, circuit design is considerably simplified if the shunt conductance of a capacitor can be ignored (i.e. R ! 1) and the capacitor therefore regarded as an open circuit for direct current.
Since capacitance C of a single parallel plate capacitor is given by: 
reducing the thickness d of a dielectric film increases the capacitance, but decreases the resistance. It also reduces the voltage the capacitor can withstand without breakdown 
ny material will eventually break down, usually destructively, when subjected to a sufficiently large electric field. A spark may occur at breakdown, which produces a hole through the film. The metal film forming the metal plates may be welded together at the point of breakdown.
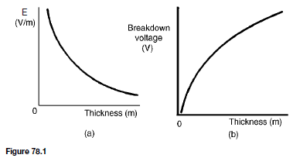
Breakdown depends on electric field strength E 1where E 
so thinner films will break down with smaller voltages across them. This is the main reason for limiting the voltage that may be applied to a capacitor. All practical capacitors have a safe working voltage stated on them, generally at a particular maximum temperature. Figure 78.1 shows the typical shapes of graphs expected for electric field strength E plotted against thickness and for break- down voltage plotted against thickness. The shape of the curves depend on a number of factors, and these include:
(i) the type of dielectric material,
(ii) the shape and size of the conductors associated with it,
(iii) the atmospheric pressure,
(iv) the humidity/moisture content of the material,
(v) the operating temperature.
Dielectric strength is an important factor in the design of capacitors as well as transformers and high voltage insulators, and in motors and generators.
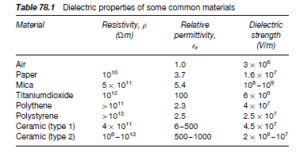
Dielectrics vary in their ability to withstand large fields. Some typical values of dielectric strength, together with resistivity and relative permittivity
are shown in Table 78.1. The ceramics have very high relative permittivities and they tend to be ‘ferroelectric’, i.e. they do not lose their polarities when the electric field is removed. When ferroelectric effects are present, the charge on a capacitor is given by: Q D (CV) C (remanent polarisation). These dielectrics often possess an appreciable negative temperature coefficient of resistance. Despite this, a high permittivity is often very desirable and ceramic dielectrics are widely used.
Thermal Effects
As the temperature of most dielectrics is increased, the insulation resistance falls rapidly. This causes the leakage current to increase, which generates further heat. Eventually a condition known as thermal avalanche or thermal runaway may develop, when the heat is generated faster than it can be dissipated to the surrounding environment. The dielectric will burn and thus fail. Thermal effects may often seriously influence the choice and application of insulating materials. Some important factors to be considered include:
(i) the melting-point (for example, for waxes used in paper capacitors),
(ii) aging due to heat,
(iii) the maximum temperature that a material will withstand without serious deterioration of essential properties,
(iv) flash-point or ignitability,
(v) resistance to electric arcs,
(vi) the specific heat capacity of the material,
(vii) thermal resistivity,
(viii) the coefficient of expansion,
(ix) the freezing-point of the material.
Mechanical Properties
Mechanical properties determine, to varying degrees, the suitability of a solid material for use as an insulator: tensile strength, transverse strength, shearing strength and compressive strength are often specified. Most solid insulations have a degree of inelasticity and many are quite brittle, thus it is often necessary to consider features such as compressibility, deformation under bending stresses, impact strength and extensibility, tearing strength, machinability and the ability to fold without damage.
Types of Practical Capacitor
Practical types of capacitor are characterised by the material used for their dielectric. The main types include: variable air, mica, paper, ceramic, plastic, titanium oxide and electrolytic. Refer back to chapter 44, page 241, for a description of each type.
Liquid Dielectrics and Gas Insulation
Liquid dielectrics used for insulation purposes include refined mineral oils, silicone fluids and synthetic oils such as chlorinated diphenyl. The principal uses of liquid dielectrics are as a filling and cooling medium for transformers, capacitors and rheostats, as an insulating and arc-quenching medium in switchgear such as circuit breakers, and as an impregnant of absorbent insulations — for example, wood, slate, paper and pressboard, used mainly in transformers, switchgear, capacitors and cables.
Two gases used as insulation are nitrogen and sulphur hexafluoride. Nitro- gen is used as an insulation medium in some sealed transformers and in power cables, and sulphur hexafluoride is finding increasing use in switchgear both as an insulant and as an arc-extinguishing medium.
Dielectric Loss and Loss Angle
In capacitors with solid dielectrics, losses can be attributed to two causes:
(i) dielectric hysteresis, a phenomenon by which energy is expended and heat produced as the result of the reversal of electrostatic stress in a dielectric subjected to alternating electric stress — this loss is analogous to hysteresis loss in magnetic materials;
(ii) leakage currents that may flow through the dielectric and along surface paths between the terminals.
The total dielectric loss may be represented as the loss in an additional resistance connected between the plates. This may be represented as either a small resistance in series with an ideal capacitor or as a large resistance in parallel with an ideal capacitor.
Series representation
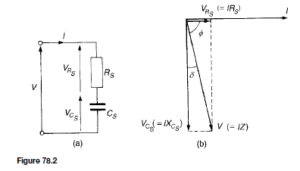
The circuit and phasor diagrams for the series representation are shown in Figure 78.2. The circuit phase angle is shown as angle ¢. If resistance RS is
zero then current I would lead voltage V by 90°, this being the case of a perfect capacitor. The difference between 90° and the circuit phase angle ¢ is the angle shown as υ. This is known as the loss angle of the capacitor, i.e.
For example, the equivalent series circuit for a particular capacitor consists of a 1.5 Q resistance in series with a 400 pF capacitor at a frequency of 8 MHz.
From equation (1), for a series equivalent circuit,
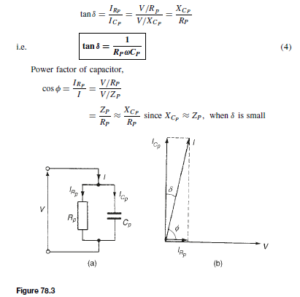
Parallel representation
The circuit and phasor diagrams for the parallel representation are shown in Figure 78.3. From the phasor diagram,
For example, a capacitor has a loss angle of 0.025 rad, and when it is connected across a 5 kV, 50 Hz supply, the power loss is 20 W. The component values of the equivalent parallel circuit is determined as follows:
