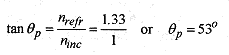Reflection, Refraction, and Polarization
In the study of reflection and refraction it is very convenient to depict light as rays. A light ray represents the path of a thin beam (ray) of light. This ray construct is very convenient in understanding reflection and refraction as well as images formed by mirrors and lenses.
Reflection and Refraction
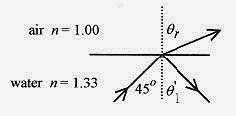
When light strikes a surface such as an air-glass or air-water interface, part of the incident light is reflected and part is refracted. Reflection of light at any interface follows a very simple law. The angle of incidence equals the angel of reflection with these angles measured from the normal to the surface. Incident and reflected rays are shown in Fig. 44-1.
Fig. 44-1
44-1 A ray of light is incident on a reflecting surface at 70° with respect to the surface. What is the angle of the reflected ray?
Solution: The 70° with respect to the surface is 20° with respect to the normal so the reflected beam is 20° from the normal.
The refracted (or bent) ray is the one that enters the new medium. The angular relationship between the incident and refracted ray is given by Snell’s law 
where the n1 and n2 are the indexes of refraction of the two media. The index of refraction is a property of the material. Figure 44-1 contains some index of refraction values.
In addition to describing refraction, the index of refraction is also the ratio of the velocity of light in vacuum to the velocity of light in the indexed medium. 
44-2 What are the angles of reflection and refraction for a light ray in air incident on glass at an angle of 35°?
Solution: The angle of incidence is measured from the normal so the angle of reflection is 35° The angle of refraction is from Snell’s law n1 sin θ1 = n2 sin θ2 
<><><><><><><><><><><><>
In passing from a medium of lower index of refraction to one with higher index of refraction the light bends toward the normal and vice versa. This is best illustrated in problem 44-3.
44-3 A light ray in water is incident on the water-air interface at an angle of 45°. What is the angle of reflection in the water and refraction into the air?
Fig 44-2
Solution: The problem is diagrammed in Fig. 44-2. The incident angle equals the reflected angle, so θ1 = 45° The refracted angle is from Snell’s law
This last problem suggests that there is an angle of incidence where there is no refracted ray; the refracted ray follows the surface. Beyond this critical angle, as it is called, all light will be reflected back into the water. Fiber-optic cable is made of light transmitting material with an index greater than one, so that light injected at the end of the cable will be internally reflected many times over its entire length.
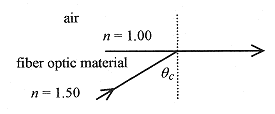
44-4 Find the critical angle for a fiber optic material with index 1.50.
Fig 44-3
Solution: The critical angle is the one where the angle of refraction is 90°. Applying Snell’s law 
Any beam that strikes the fiber-air interface at an angle greater than 42° will be internally reflected down the fiber.
<><><><><><><><><><><><>
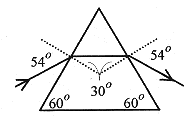
Figure 44-4 shows a ray of light incident on a equilateral triangular glass prism at an angle of 54°.
Fig. 44-4
Applying Snell’s law to find the refracted ray angle yields 1.00 sin 54° = 1.62 sin θr, or θr = 30°. This means that the ray travels parallel to the base inside the prism and is refracted at 54° on exit.
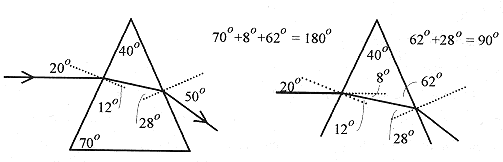
Now change the problem slightly by having the ray incident parallel to the base of a prism with the base angles 70°.
Fig. 44-5
From the geometry the angle of incidence for the ray entering the prism is 20°, and applying Snell’s law 1.00sin20° = 1.62sinθr, θr = 12°. Again from the geometry, the angle of incidence for the ray leaving the prism is 28°, and applying Snell’s law 1.62sin28° = 1.00sinθr, θr = 50°. A prism bends light incident parallel to its base toward the base.
If a collection of parallel rays were incident on the face of this prism they would all be refracted toward a line extending from the base. Further, if the incident and exit faces were curved, all parallel rays could be focused at one point. Two curved-face prisms placed base-to-base are a lens of sorts focusing parallel rays to a single point.
The index of refraction, or wave speed, depends slightly on the wavelength of the light. A ray of sunlight passing through a prism exhibits the dispersion effect, whereby different wavelength components of the sunlight are refracted at different angles producing a rainbow of colors from red to violet.
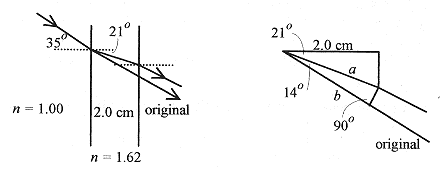
44-5 Light is incident at an angle of 35° on a slab of glass 2.0cm thick. Part of the light travels through the glass and part along its original direction beside the glass. Find the path of the two rays, the velocity of the ray in the glass, and the time difference between the two when they emerge from the opposite side of the glass. The geometry is shown in Fig. 44-6.
Fig 44-6
Solution: Apply Snell’s law to find the path through the slab. 1.00sin 35° = 1.62sinθr, or θr=21°. Because of symmetry, the ray through the slab exits parallel to the original ray. The velocity of the ray in the glass is from n = c/v, or v = c/n=3.0 × 108 m/s/1.62=1.85×108 m/s. Now that the velocities are known the time difference requires finding the distance the rays travel.
The distance a (the path through the slab) comes from cos21° = 2.0cm/a, or a = 2.14 cm. Construct a line perpendicular to the two rays at the point where the refracted one leaves the slab.
The distance b in the original ray direction comes from cos14° = b/2.14cm, or b = 2.08cm.
The time for the refracted beam is τr = 0.0214m/1.85 × 108 m/s = 11.6 × 10-11S.
The time for the unaltered beam is τ=0.0208m/3.0 × 108 m/s = 6.9 × 10-11S.
The time delay is 4.7 × 10-11 S.
Polarization
Light from a light bulb or the sun is circularly polarized. This means that if you could look at the electric vectors there would be no preferred direction. The electric vectors would be randomly oriented in space. Polarization is described in terms of electric vectors rather than magnetic vectors. A radio transmitting antenna that is vertical produces waves with vertical electric vectors, and the radiation from this antenna is vertically polarized.
Polarization is usually studied in the context of light. There are two ways to polarize light. It can be polarized by passing through a material that contains molecules all oriented in the same direction that absorb the electric vector (in this one direction) in the light. These materials are called polaroids. Polaroid sun glasses are made of a polaroid that absorbs the electric vector in one direction.
Light, and other electromagnetic waves are more or less polarized by reflection, depending on the angle of incidence and the index of refraction. When unpolarized or circularly polarized light is incident from air onto water the reflected beam is of lowered intensity and polarized with the electric vector parallel to the reflecting surface. The refracted beam is transmitted with a diminished intensity and is partially polarized by the reduction of the electric vector in the plane of the reflecting surface. The angle of incidence for complete polarization occurs when the angle between the reflected and refracted beams is 90°. The geometry of the situation is shown in Fig. 44-7.
The criterion for complete polarization is that θr + θp = 90°. Snell’s law requires that ninc sin θp = nrefr sinθr, but θr = 90° – θp and sin θr = sin(90° – θp) = cosθp, so nincsinθp = nrefr cosθp or 
Fig. 44-7
This polarization law is known as Brewster’s law, and the angle of polarization is called the Brewster angle. In working problems be careful not to invert the fraction of the indexes of refraction.
44-6 What is the polarization angle for light reflected from water?
Solution: 
<><><><><><><><><><><><>
44-7 A beam of unpolarized light in water is incident on what is reported to be diamond. By means of polaroids the angle (of incidence) for complete polarization is determined to be 61°. Is this diamond?
Solution: For light in water reflected from diamond the Brewster angle should be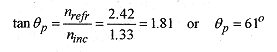
From the indexes of refraction given in Fig. 44-1 we conclude that this is diamond.