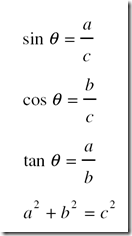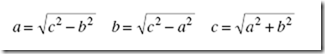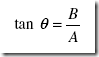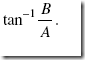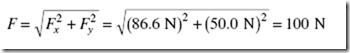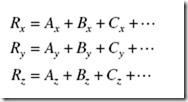Vectors
In This Chapter:
✔ Scalar and Vector Quantities
✔ Vector Addition: Graphical Method
✔ Trigonometry
✔ Pythagorean Theorem
✔ Vector Addition: Trigonometric Method
✔ Resolving a Vector
✔ Vector Addition: Component Method
Scalar and Vector Quantities
A scalar quantity has only magnitude and is completely specified by a number and a unit. Examples are mass (a stone has a mass of 2 kg), volume (a bottle has a volume of 1.5 liters), and frequency (house current has a frequency of 60 Hz). Scalar quantities of the same kind are added by using ordinary arithmetic.
A vector quantity has both magnitude and direction. Examples are displacement (an airplane has flown 200 km to the southwest), velocity (a car is moving 60 km/h to the north), and force (a person applies an upward force of 25 newtons to a package). Symbols of vector quantities are printed in boldface type (v = velocity, F = force). When vec- tor quantities of the same kind are added, their directions must be taken into account.
Vector Addition: Graphical Method
A vector is represented by an arrow whose length is proportional to a certain vector quantity and whose direction indicates the direction of the quantity.
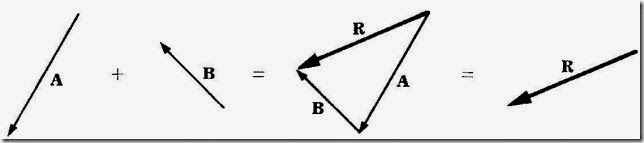
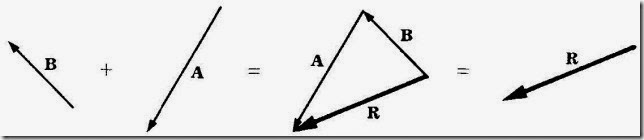
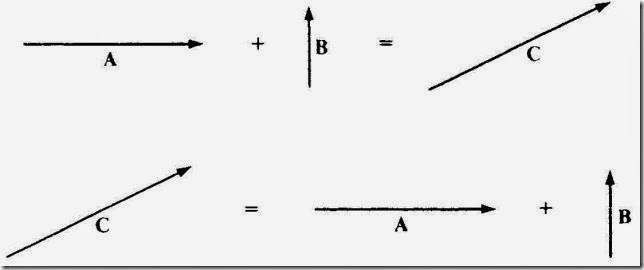
To add vector B to vector A, draw B so that its tail is at the head of A. The vector sum A + B is the vector R that joins the tail of A and the head of B (Figure 1-1). Usually, R is called the resultant of A and B. The order in which A and B are added is not significant, so that A + B = B + A (Figures 1-1 and 1-2).
Figure 1-1
Figure 1-2
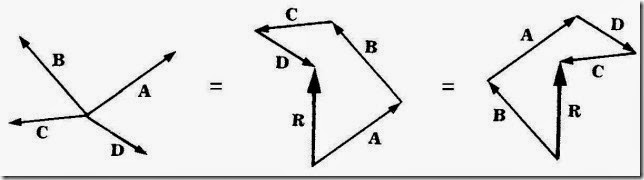
Exactly the same procedure is followed when more than two vectors of the same kind are to be added. The vectors are strung together head to tail (being careful to preserve their correct lengths and directions), and the resultant R is the vector drawn from the tail of the first vector to the head of the last. The order in which the vectors are added does not matter (Figure 1-3).
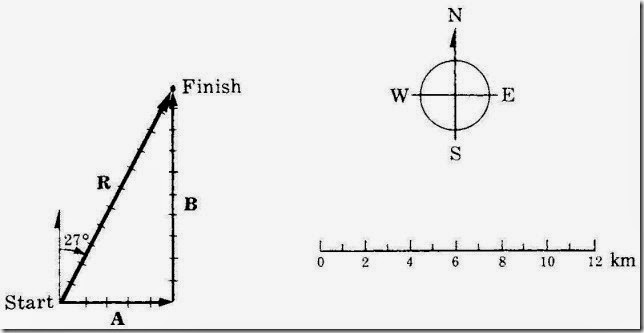
Solved Problem 1.1 A woman walks eastward for 5 km and then north- ward for 10 km. How far is she from her starting point? If she had walked directly to her destination, in what direction would she have headed?
Solution. From Figure 1-4, the length of the resultant vector R corresponds to a distance of 11.2 km, and a protractor shows that its direction is 27° east of north.
Figure 1-4
Trigonometry
Although it is possible to determine the magnitude and direction of the resultant of two or more vectors of the same kind graphically with ruler or protractor, this procedure is not very exact. For accurate results, it is necessary to use trigonometry.
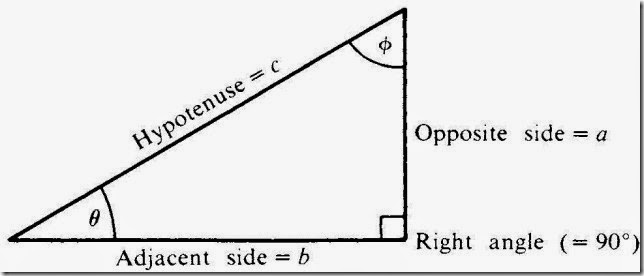
A right triangle is a triangle whose two sides are perpendicular. The hypotenuse of a right triangle is the side opposite the right angle, as in Figure 1-5; the hypotenuse is always the longest side.
Figure 1-5
The three basic trigonometric functions—the sine, cosine, and tan- gent of an angle—are defined in terms of the right triangle of Figure 1-5 as follows:
The inverse of a trigonometric function is the angle whose function is given. Thus the inverse of sin q is the angle q. The names and abbre- viations of the inverse trigonometric functions are as follows:
Remember
In trigonometry, an expression such as sin−1x does not signify 1/(sin x), even though in algebra, the expo- nent −1 signifies a reciprocal.
Pythagorean Theorem
The Pythagorean theorem states that the sum of the squares of the short sides of a right triangle is equal to the square of its hypotenuse. For the triangle of Figure 1-5,
a2 + b2 = c2
Hence, we can always express the length of any of the sides of a right tri- angle in terms of the lengths of the other sides:
Another useful relationship is that the sum of the interior angles of any triangle is 180°. Since one of the angles in a right triangle is 90°, the sum of the other two must be 90°. Thus, in Figure 1-5, q + f = 90°.
Of the six quantities that characterize a triangle—three sides and three angles—we must know the values of at least three, including one of the sides, in order to calculate the others. In a right triangle, one of the angles is always 90°, so all we need are the lengths of any two sides or the length of one side plus the value of one of the other angles to find the other sides and angles.
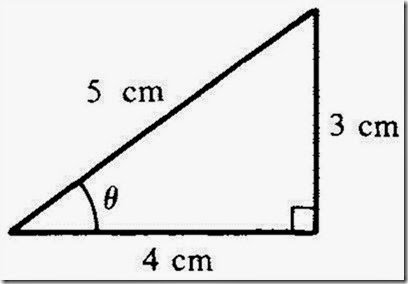
Solved Problem 1.2 Find the values of the sine, cosine, and tangent of angle q in Figure 1-6.
Solution.
Vector Addition: Trigonometric Method
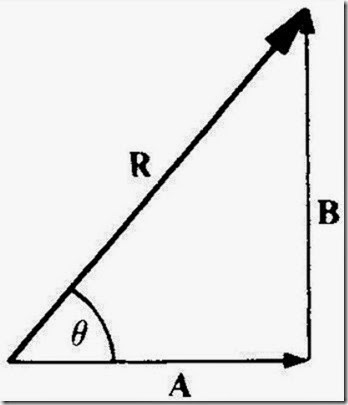
It is easy to apply trigonometry to find the resultant R of two vectors A and B that are perpendicular to each other. The magnitude of the resultant is given by the Pythagorean theorem as: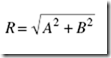
and the angle between R and A (Figure 1-7) may be found from
by examining a table of tangents or by using a calculator to determine
Resolving a Vector
Just as two or more vectors can be added to yield a single resultant vector, so it is possible to break up a single vector into two or more other vectors. If vectors A and B are together equivalent to vector C, then vector C is equivalent to the two vectors A and B (Figure 1-8). When a vector is replaced by two or more others, the process is called resolving the vector, and the new vectors are known as the components of the initial vector.
Figure 1-8
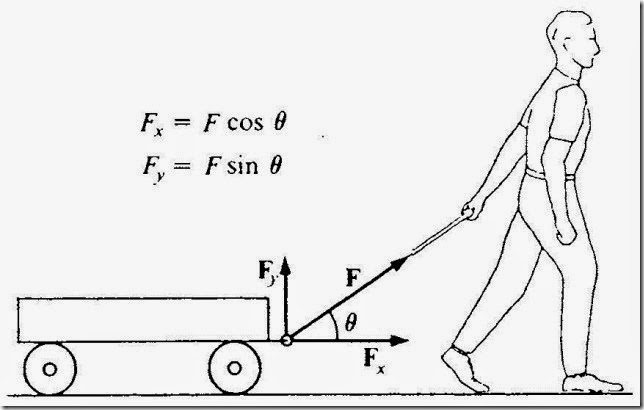
The components into which a vector is resolved are nearly always chosen to be perpendicular to one another. Figure 1-9 shows a wagon be- ing pulled by a man with force F. Because the wagon moves horizontal- ly, the entire force is not effective in influencing its motion.
Figure 1-9
The force F may be resolved into two component vectors Fx and Fy, where
Fx = horizontal component of F
Fy = vertical component of F
The magnitudes of these components are
Evidently, the component Fx is responsible for the wagon’s motion, and if we were interested in working out the details of this motion, we would need to consider only Fx.
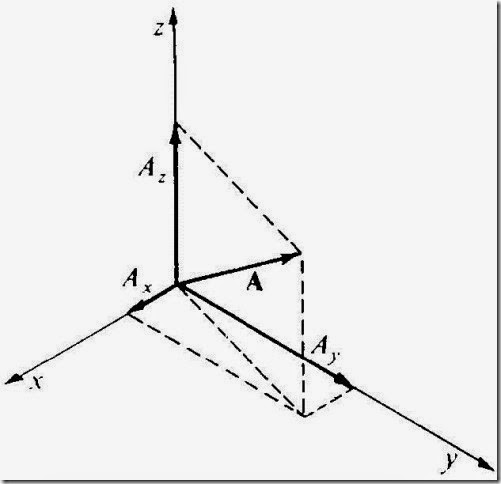
In Figure 1-9, the force F lies in a vertical plane, and the two com- ponents Fx and Fy are enough to describe it. In general, however, three mutually perpendicular components are required to completely describe the magnitude and direction of a vector quantity. It is customary to call the directions of these components the x, y, and z axes, as in Figure 1-10. The component of some vector A in these directions are accordingly de- noted Ax, Ay, and Az. If a component falls on the negative part of an axis, its magnitude is considered negative. Thus, if Az were downward in Fig- ure 1-10 instead of upward and its length were equivalent to, say, 12 N,
we would write Az = −12 N. (The newton (N) is the SI unit of force; it is equal to 0.225 lb.)
Figure 1-10
Solved Problem 1.3 The man in Figure 1-9 exerts a force of 100 N on the wagon at an angle of q = 30° above the horizontal. Find the horizon- tal and vertical components of this force.
Solution. The magnitudes of Fx and Fy are, respectively,
We note that Fx + Fy = 136.6 N although F itself has the magnitude F = 100 N. What is wrong? The answer is that nothing is wrong; because Fx and Fy are just the magnitudes of the vectors Fx and Fy, it is meaningless to add them. However, we can certainly add the vectors Fx and Fy to find the magnitude of their resultant F. Because Fx and Fy are perpendicular,
as we expect.
Vector Addition: Component Method
When vectors to be added are not perpendicular, the method of addition by components described below can be used. There do exist trigonometric procedures for dealing with oblique triangles (the law of sines and the law of cosines), but these are not necessary since the component method is entirely general in its application.
To add two or more vectors A, B, C, … by the component method, follow this procedure:
1. Resolve the initial vectors into components in the x, y, and z directions.
2. Add the components in the x direction to give Rx, add the components in the y direction to give Ry, and add the components in the z direction to give Rz. That is, the magnitudes of Rx, Ry, and Rz are given by, respectively,
3. Calculate the magnitude and direction of the resultant R from its components Rx, Ry, and Rz by using the Pythagorean theorem: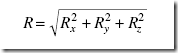
If the vectors being added all lie in the same plane, only two components need to be considered.