Introduction
A filter is a network designed to pass signals having frequencies within certain bands (called passbands) with little attenuation, but greatly attenuates signals within other bands (called attenuation bands or stopbands).
A filter is frequency sensitive and is thus composed of reactive elements. Since certain frequencies are to be passed with minimal loss, ideally the inductors and capacitors need to be pure components since the presence of resistance results in some attenuation at all frequencies.
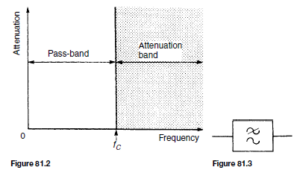
Between the pass band of a filter, where ideally the attenuation is zero, and the attenuation band, where ideally the attenuation is infinite, is the cut- off frequency, this being the frequency at which the attenuation changes from zero to some finite value.
A filter network containing no source of power is termed passive, and one containing one or more power sources is known as an active filter network.
Filters are used for a variety of purposes in nearly every type of electronic communications and control equipment. The bandwidths of filters used in communications systems vary from a fraction of a hertz to many megahertz,
depending on the application.
There are four basic types of filter sections:
(a) low-pass
(b) high-pass
(c) band-pass
(d) band-stop
Low-pass Filters
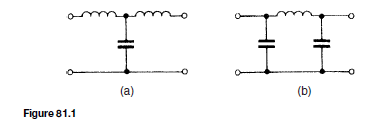
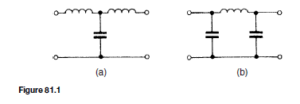
Figure 81.1 shows simple unbalanced T- and n-section filters using series inductors and shunt capacitors. If either section is connected into a net- work and a continuously increasing frequency is applied, each would have a frequency-attenuation characteristic as shown in Figure 81.2. This is an ideal characteristic and assumes pure reactive elements. All frequencies are seen
to be passed from zero up to a certain value without attenuation, this value being shown as fC, the cut-off frequency; all values of frequency above fC are attenuated. It is for this reason that the networks shown in Figures 81.1(a) and (b) are known as low-pass filters.
The electrical circuit diagram symbol for a low-pass filter is shown in Figure 81.3.
Summarising, a low-pass filter is one designed to pass signals at frequencies below a specified cut-off frequency.
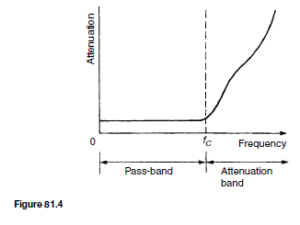
In practise, the characteristic curve of a low-pass prototype filter section looks more like that shown in Figure 81.4. The characteristic may be improved somewhat closer to the ideal by connecting two or more identical sections in cascade. This produces a much sharper cut-off characteristic, although the attenuation in the pass band is increased a little.
When rectifiers are used to produce the d.c. supplies of electronic systems, a large ripple introduces undesirable noise and may even mask the effect of the
signal voltage. Low-pass filters are added to smooth the output voltage wave- form, this being one of the most common applications of filters in electrical circuits.
Filters are employed to isolate various sections of a complete system and thus to prevent undesired interactions. For example, the insertion of low- pass decoupling filters between each of several amplifier stages and a common power supply reduces interaction due to the common power supply impedance.
High-pass Filters
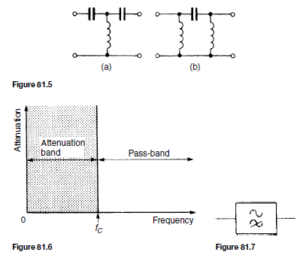
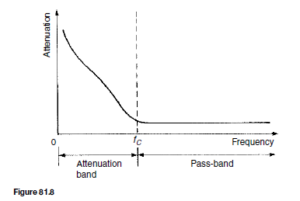
Figure 81.5 shows simple unbalanced T- and n-section filters using series capacitors and shunt inductors. If either section is connected into a network and a continuously increasing frequency is applied, each would have a frequency- attenuation characteristic as shown in Figure 81.6.
Once again this is an ideal characteristic assuming pure reactive elements.
All frequencies below the cut-off frequency fc are seen to be attenuated and all frequencies above fc are passed without loss. It is for this reason that the networks shown in Figures 81.5(a) and (b) are known as high-pass filters.
The electrical circuit diagram symbol for a high-pass filter is shown in Figure 81.7.
Summarising, a high-pass filter is one designed to pass signals at frequencies above a specified cut-off frequency.
The characteristic shown in Figures 81.6 is ideal in that it is assumed that there is no attenuation at all in the pass-bands and infinite attenuation in the attenuation band. Both of these conditions are impossible to achieve in practice. Due to resistance, mainly in the inductive elements the attenuation in the pass-band will not be zero, and in a practical filter section the attenuation in the attenuation band will have a finite value. In addition to the resistive loss there is often an added loss due to mismatching.
Ideally when a filter is inserted into a network it is matched to the impedance of that network. However the characteristic impedance of a filter section will vary with frequency and the termination of the section may be an impedance that does not vary with frequency in the same way. To minimise losses due to resistance and mismatching, filters are used under image impedance conditions as far as possible (see Chapter 80).
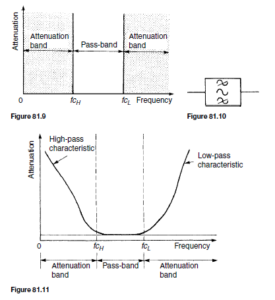
Figure 81.6 showed an ideal high-pass filter section characteristic of attenuation against frequency. In practise, the characteristic curve of a high-pass prototype filter section would look more like that shown in Figure 81.8.
Band-pass Filters
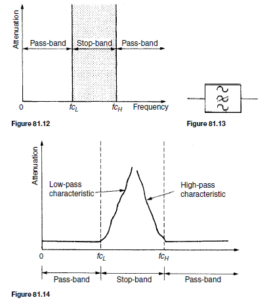
A band-pass filter is one designed to pass signals with frequencies between two specified cut-off frequencies. The characteristic of an ideal band-pass filter is shown in Figure 81.9.
Such a filter may be formed by cascading a high-pass and a low-pass filter. fCH is the cut-off frequency of the high-pass filter and fCL is the cut-off frequency of the low-pass filter. As can be seen, for a band-pass filter fCL > fCH , the pass-band being given by the difference between these values.
The electrical circuit diagram symbol for a band-pass filter is shown in Figure 81.10.
A typical practical characteristic for a band-pass filter is shown in Figure 81.11.
Crystal and ceramic devices are used extensively as band-pass filters. They are common in the intermediate-frequency amplifiers of v.h.f. radios where a precisely defined bandwidth must be maintained for good performance.
Band-stop Filters
A band-stop filter is one designed to pass signals with all frequencies except those between two specified cut-off frequencies. The characteristic of an ideal band-stop filter is shown in Figure 81.12.
Such a filter may be formed by connecting a high-pass and a low-pass filter in parallel. As can be seen, for a band-stop filter fCH > fCL , the stop-band being given by the difference between these values.
The electrical circuit diagram symbol for a band-stop filter is shown in Figure 81.13.
A typical practical characteristic for a band-stop filter is shown in Figure 81.14.
Sometimes, as in the case of interference from 50 Hz power lines in an audio system, the exact frequency of a spurious noise signal is known. Usually such interference is from an odd harmonic of 50 Hz, for example, 250 Hz. A sharply tuned band-stop filter, designed to attenuate the 250 Hz noise signal, is used to minimise the effect of the output. A high-pass filter with cut-off frequency greater than 250 Hz would also remove the interference, but some of the lower frequency components of the audio signal would be lost as well.