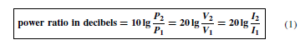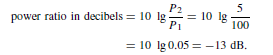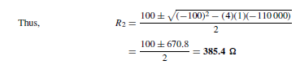Introduction
An attenuator is a device for introducing a specified loss between a signal source and a matched load without upsetting the impedance relationship necessary for matching. The loss introduced is constant irrespective of frequency; since reactive elements (L or C) vary with frequency, it follows that ideal attenuators are networks containing pure resistances. A fixed attenuator section is usually known as a ‘pad’.
Attenuation is a reduction in the magnitude of a voltage or current due to its transmission over a line or through an attenuator. Any degree of attenuation may be achieved with an attenuator by suitable choice of resistance values but the input and output impedances of the pad must be such that the impedance conditions existing in the circuit into which it is connected are not disturbed. Thus an attenuator must provide the correct input and output impedances as well as providing the required attenuation.
Two-port Networks
Networks in which electrical energy is fed in at one pair of terminals and taken out at a second pair of terminals are called two-port networks. Thus an attenuator is a two-port network, as are transmission lines, transformers and electronic amplifiers. If a network contains only passive circuit elements, such as in an attenuator, the network is said to be passive; if a network contains a source of e.m.f., such as in an electronic amplifier, the network is said to be active.
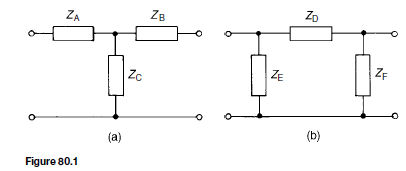
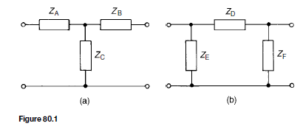
Figure 80.1(a) shows a T-network, which is termed symmetrical if ZA D ZB and Figure 80.1(b) shows a .r-network which is symmetrical if ZE= ZF. If ZA 6D ZB in Figure 80.1(a), and ZE 6D ZF in Figure 80.1(b), the sections are termed asymmetrical. Both networks shown have one common terminal, which may be earthed, and are therefore said to be unbalanced. The balanced
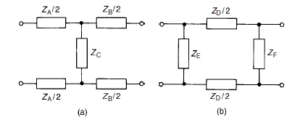
form of the T-network is shown in Figure 80.2(a) and the balanced form of the .r-network is shown in Figure 80.2(b).
Characteristic Impedance
The input impedance of a network is the ratio of voltage to current (in complex form) at the input terminals. With a two-port network the input impedance often varies according to the load impedance across the output terminals. For any passive two-port network it is found that a particular value of load impedance can always be found which will produce an input impedance having the same value as the load impedance. This is called the iterative impedance for an asymmetrical network and its value depends on which pair of terminals is taken to be the input and which the output (there are thus two values of iterative impedance, one for each direction). For a symmetrical network there is only one value for the iterative impedance and this is called the characteristic impedance of the symmetrical two-port network.
Logarithmic Ratios
The ratio of two powers P1 and P2 may be expressed in logarithmic form as shown in chapter 50. Let P1 be the input power to a system and P2 the output power.
If logarithms to base 10 are used then
For example, if, say, 5% of the power supplied to a cable appears at the output terminals then the attenuation in decibels is determined as follows:
From equation (1),
Hence the attenuation (i.e. power loss) is 13 dB.
In another example, if an amplifier has a gain of 15 dB and the input power is 12 mW, the output power is determined as follows:
From equation (1),
The attenuation of filter sections and along a transmission line are of an exponential form and it is in such applications that the unit of the neper is used (see chapters 81 and 83).
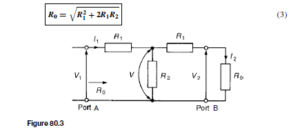
Symmetrical T -attenuator
For the symmetrical T-pad attenuator is shown in Figure 80.3, the characteristic impedance R0 is given by:
For example, a T-section symmetrical attenuator pad to provide a voltage attenuation of 20 dB and having a characteristic impedance of 600 Q is designed as follows:
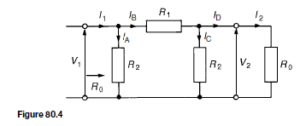
Symmetrical p-attenuator
For the symmetrical .r-attenuator shown in Figure 80.4 the characteristic impedance R0 is given by:
For example, if a .r-section symmetrical attenuator is required to provide a voltage attenuation of 25 dB and have a characteristic impedance of 600 Q, then:
Insertion Loss
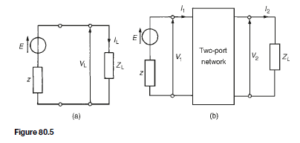
Figure 80.5(a) shows a generator E connected directly to a load ZL . Let the current flowing be IL and the p.d. across the load VL . z is the internal impedance of the source.
Figure 80.5(b) shows a two-port network connected between the generator E and load ZL . The current through the load, shown as I2 , and the p.d. across the load, shown as V2 will generally be less than current IL and voltage VL of Figure 80.5(a), as a result of the insertion of the two-port network between generator and load.
When the two-port network is terminated in its characteristic impedance Z0 the network is said to be matched. In such circumstances the input impedance is also Z0, thus the insertion loss is simply the ratio of input to output voltage
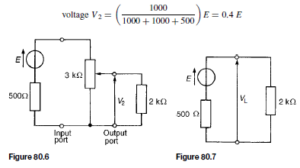
For example, a 0– 3 kQ rheostat is connected across the output of a signal generator of internal resistance 500 Q. If a load of 2 kQ is connected across the rheostat, the insertion loss at a tapping of, say, 2 kQ is determined as follows:
The circuit diagram is shown in Figure 80.6. Without the rheostat in the ircuit the voltage across the 2 kQ load, VL (see Figure 80.7), is given by:
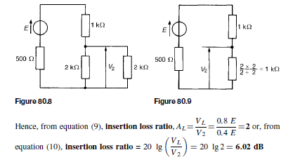
With the 2 kQ tapping, the network of Figure 80.7 may be redrawn as shown in Figure 80.8, which in turn is simplified as shown in Figure 80.9. From Figure 80.9,
Asymmetrical T – and p-sections
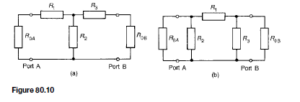
Figure 80.10(a) shows an asymmetrical T-pad section where resistance R1 6D 3. Figure 80.10(b) shows an asymmetrical .r-section where R2 6D R3.
When viewed from port A, in each of the sections, the output impedance is ROB; when viewed from port B, the input impedance is ROA. Since the sections are asymmetrical ROA does not have the same value as ROB.
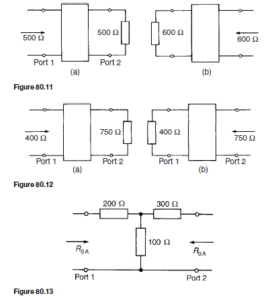
Iterative impedance is the term used for the impedance measured at ne port of a two-port network when the other port is terminated with an impedance of the same value. For example, the impedance looking into port 1 of Figure 80.11(a) is, say, 500 Q when port 2 is terminated in 500 Q and the impedance looking into port 2 of Figure 80.11(b) is, say, 600 Q when port 1 is terminated in 600 Q. (In symmetric T- and .r-sections the two iterative impedances are equal, this value being the characteristic impedance of the section).
An image impedance is defined as the impedance which, when connected to the terminals of a network, equals the impedance presented to it at the opposite terminals. For example, the impedance looking into port 1 of Figure 80.12(a) is, say, 400 Q when port 2 is terminated in, say 750 Q, and the impedance seen looking into port 2 (Figure 80.12(b)) is 750 Q when port
1 is terminated in 400 Q. An asymmetrical network is correctly terminated when it is terminated in its image impedance. (If the image impedances are equal, the value is the characteristic impedance).
For example, an asymmetrical T-section attenuator is shown in Figure 80.13. The image and iterative impedances are determined as follows: The image impedance ROA seen at port 1 in Figure 80.13 is given by equation (4): ![]() where ROC and RSC refer to port 2 being respectively open-circuited and short circuited.
where ROC and RSC refer to port 2 being respectively open-circuited and short circuited.
Thus the iterative impedances of the section shown in Figure 80.13 are 285.4 and 385.4
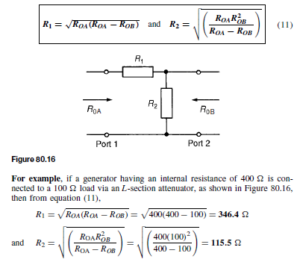
The L-section Attenuator
For the L-section attenuator shown in Figure 80.16,
Two-port Networks in Cascade
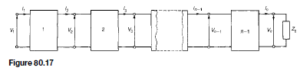
Often two-port networks are connected in cascade, i.e. the output from the first network becomes the input to the second network, and so on, as shown in Figure 80.17. Thus an attenuator may consist of several cascaded sections so as to achieve a particular desired overall performance.
If the cascade is arranged so that the impedance measured at one port and the impedance with which the other port is terminated have the same
value, then each section (assuming they are symmetrical) will have the same characteristic impedance Z0 and the last network will be terminated in Z0. Thus each network will have a matched termination and hence the attenuation