Kruskal’s Algorithm -to find minimum spanning tree.

Kruskal’s Algorithm

-to find minimum spanning tree

Algorithm:

ALGORITHM Kruskal (G)

//Kruskal’s algorithm for constructing a MST

//Input: A weighted connected graph G = { V, E }

//Output: ET the set of edges composing a MST of G

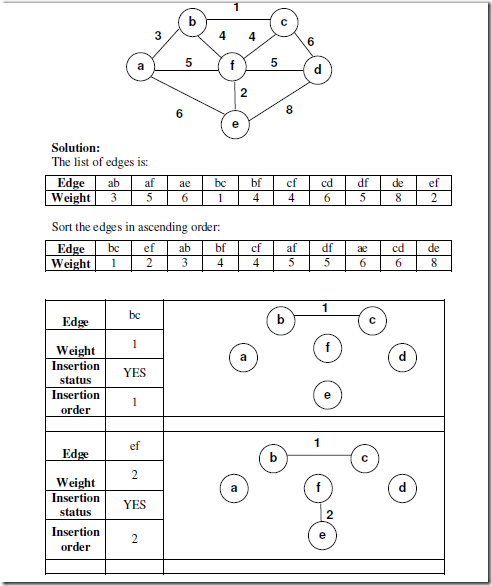
Sort E in ascending order of the edge weights

// initialize the set of tree edges and its size

The method:

STEP 1: Sort the edges by increasing weight

STEP 2: Start with a forest having |V| number of trees.

STEP 3: Number of trees are reduced by ONE at every inclusion of an edge At each stage:

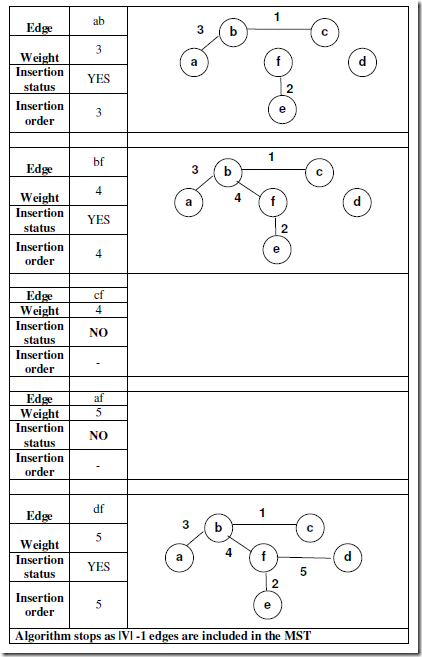
• Among the edges which are not yet included, select the one with minimum weight AND which does not form a cycle.

• the edge will reduce the number of trees by one by combining two trees of the forest

Algorithm stops when |V| -1 edges are included in the MST i.e : when the number of trees in the forest is reduced to ONE.

Example:

Apply Kruskal’s algorithm for the following graph to find MST.

Efficiency:

Efficiency of Kruskal’s algorithm is based on the time needed for sorting the edge weights of a given graph.

• With an efficient sorting algorithm: Efficiency: Θ(|E| log |E| )

Conclusion:

• Kruskal’s algorithm is an “edge based algorithm”
• Prim’s algorithm with a heap is faster than Kruskal’s algorithm.