THE SINGLE-PHASE, THREE-WIRE SYSTEM
Nearly all residential and commercial electrical installations use a single-phase, three- wire service similar to the one shown in Figure 13–12. This type of service has a number of advantages:
1. The system provides two different voltages. The lower voltage supplies lighting and small-appliance loads, and the higher voltage supplies heavy-appliance and single- phase motor loads.
2. There are 240 V across the outside wires. Thus, the current for a given kilowatt load can be reduced by nearly half if the load is balanced between the neutral and the two outside wires. Because of the reduction in the current, the voltage drop in the circuit conductors is reduced, and the voltage at the load is more nearly constant. In addition, the following problems are minimized: dim lights, slow heating, and unsatisfactory appliance performance.
3. A single-phase, three-wire, 120/240-V system uses 37% less copper as compared to a 120-V, two-wire system having the same capacity and transmission efficiency.
Problem 6 shows why less copper is needed in such a single-phase, three-wire circuit.
PROBLEM 6
Statement of the Problem
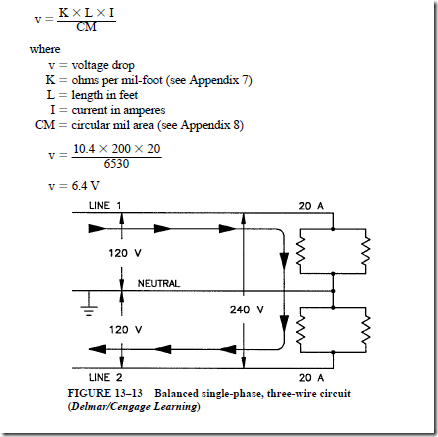
Figure 13–13 shows a balanced single-phase, three-wire circuit. Two 10-A noninductive heater units are connected to each side of this circuit. The conductors used in this circuit are no. 12 AWG wire. The distance from the source to the load is 100 ft. Determine
1. the voltage drop in the line wires.
2. the percentage voltage drop.
3. the weight of the copper used for the three-wire system.
Solution
1. The total current taken by the two noninductive heater units connected between line 1 and the neutral wire is 10 + 10 = 20 A.
The two heater units connected between line 2 and the neutral wire also take a total current of 20 A.
The current in the neutral wire of a single-phase, three-wire noninductive circuit is the difference between the currents in the two line wires. For a balanced circuit, such as that of Figure 13–13, the current in the neutral wire is zero. This means that the actual current path for the 20-A current is the two no. 12 line wires. The actual voltage drop is
2. Because the source voltage across the two outside legs of the system is 240 V, the percentage voltage drop is 6.4/240 = 0.02666 = 2.67%.
3. The weight of the copper used in the single-phase, three-wire system is determined as follows:
Weight of 200 feet of no. 12 AWG wire = 1.98 lb
Weight of 300 feet of no. 12 AWG wire = 5.94 lb
PROBLEM 7
Statement of the Problem
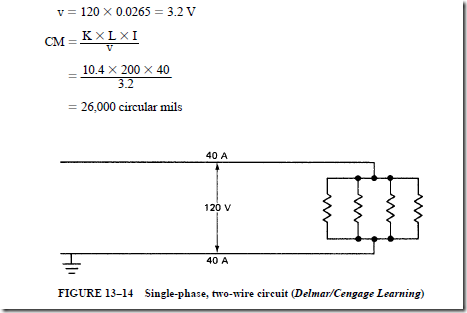
A 120-V, two-wire circuit is shown in Figure 13–14. Note that the four noninductive heater units are connected in parallel. Each heater unit takes 10 A. The allowable percentage voltage drop is 3%. This value is the same as that used in problem 6 for the single-phase, three-wire system. Determine
1. the wire size in circular mils that will give the same percentage voltage drop and, as a consequence, the same transmission efficiency as specified for the circuit in problem 6.
2. the AWG wire size of the 120-V, two-wire system.
3. the weight of the copper used in the 120-V, two-wire system.
4. the amount of copper saved by using the single-phase, three-wire system.
Solution
1. Desirable voltage drop:
2. A circular mil area of 26,000 circular mils requires no. 6 AWG wire.
3. The weight of 100 ft of no. 6 AWG wire is 7.95 lb. Therefore, the total weight of the 200 ft of wire used in this circuit is 15.9 lb.
4. The actual percentage of copper used in a single-phase, three-wire system, as com- pared with an equivalent single-phase, 120-V, two-wire system, is
Therefore, the maximum amount of copper saved by using the single-phase, three- wire system is 62.65%. The actual amount of copper saved is closer to 50% because the copper used in the three-wire, single-phase system is normally sized larger than the permitted minimum size.
Circuit with Unbalanced Loads
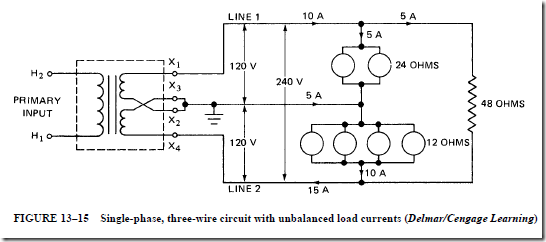
Figure 13–15 shows a single-phase, three-wire system having unbalanced noninductive lighting and heating loads from line 1 to the neutral and from line 2 to the neutral. The function of the neutral now is to maintain nearly constant voltages across the two sides of the system in the presence of different currents. For the ac noninductive circuit in Figure 13–15, the current in the grounded neutral wire is the difference between the currents in the two outside legs. Because this is an ac circuit, the arrows show only the instantaneous directions of current. For the instant shown, X is instantaneously negative and supplies 10 A to line 1. Line 2 returns 15 A to X , which is instantaneously positive. The neutral wire conducts the difference between these two line currents. This difference is 5 A.
For the instant shown in Figure 13–15, the current in the neutral wire is in the direction from the transformer to the load. Line 1 supplies a total of 10 A, 5 A to the heater load, and 5 A to the lighting load connected between line 1 and the neutral. However, 10 A is required by the lighting load connected from the neutral to line 2. Therefore, the neutral wire supplies the difference of 5 A to meet the demands of the lighting load connected
between line 2 and the neutral wire. Kirchhoff’s current law can be applied to this circuit. Recall that the current law states that the sum of the currents at any junction point in a network system is always zero.
In a single-phase, three-wire circuit, the neutral wire is always grounded. Also, it is never fused or broken at any switch control point in the circuit. This direct path to ground by way of the neutral wire means that any instantaneous high voltage, such as that due to lightning, will be instantly discharged to ground. As a result, electrical equipment and the circuit wiring are protected from major lightning damage.
Circuit with an Open Neutral
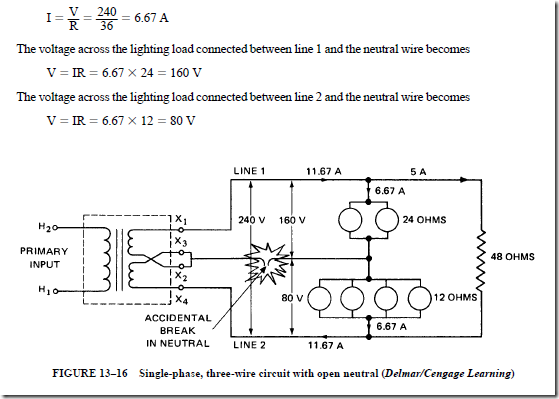
There is an even more important reason for not breaking the neutral wire. Recall that the neutral wire helps maintain balanced voltages between each line wire and the neutral wire, even with unbalanced loads. Assume that the neutral wire in Figure 13–15 is opened accidentally. The two lighting loads are now in series across 240 V.
Figure 13–16 shows the circuit of Figure 13–15, but with an open neutral. The 48-W heater unit still takes 5 A at voltage of 240 V. However, the two lighting loads act like two resistances in series across 240 V. The total resistance of the two lighting loads in series is 24 + 12 = 36 W.
The following values can be calculated for this circuit. The current is
The lighting load connected between line 1 and the neutral wire now has 160 V through it rather than its rated voltage of 120 V. This higher voltage will cause the lamps to burn out. The lighting load connected between line 2 and the neutral wire receives only 80 V, instead of 120 V. This voltage is not sufficient for adequate operation of the load. This type of unbalanced voltage condition would be common if fuses or switch control devices were placed in the neutral wire. In practice, the neutral wire is always carried as a solid conductor through the entire circuit.