Transformer Connections for Three-Phase Circuits
THE DELTA CONNECTION
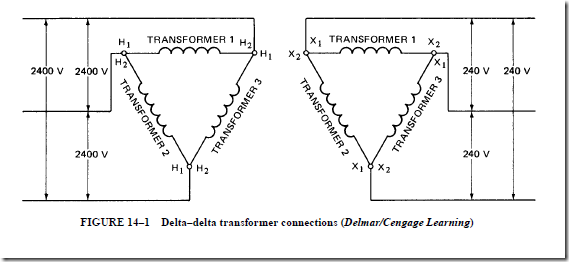
A delta–delta connection is used when three single-phase transformers are used to step down as three-phase voltage of 2400 V to 240 V, three phase.
The connections for the three single-phase transformers are shown in Figure 14–1. The primary and secondary windings of the transformers are connected in delta. The high- voltage leads of the primary winding of each transformer are marked H1 and H2. The leads of the low-voltage secondary winding of each transformer are marked X1 and X2.
Primary Winding Connections
The high-voltage primary windings are connected in a closed-delta arrangement. H1 is assumed to be the beginning of each high-voltage winding and H2 is assumed to be the end. The end (H2 ) of each primary winding is connected to the beginning (H1) of the next primary winding to form a series arrangement. One three-phase line wire is connected to each junction of two windings. In other words, the primary winding of each transformer is connected directly across the line voltage. Each of the three line voltages is 2400 V and the primary winding of each transformer is correctly rated at 2400 V. Once the high-voltage primary connections are made, the three-phase 2400-V input may be energized and tested for the correct phase rotation.
Unit 13 described the high-voltage lead (H1 ) of any transformer as being on the left when the transformer is viewed from the low-voltage side. This means that the positions of H1 and H2 are fixed. Unit 13 also explained that transformers are standardized with regard to polarity. They have additive or subtractive polarity, according to their voltage ratings and capacities in kilovolt-amperes. However, there are many exceptions to these standards. To determine whether a transformer has additive or subtractive polarity, check the terminal markings or the nameplate data.
Phase Inversion
The primary side of the delta-connected transformer may be connected so as to reverse the polarity of one of its legs. Such a phase inversion of the primary side must be corrected in the secondary side. The following method can be used to correct the polarity:
1. Determine whether the voltage output of each of the three transformers is the same as the voltage rating on the nameplate.
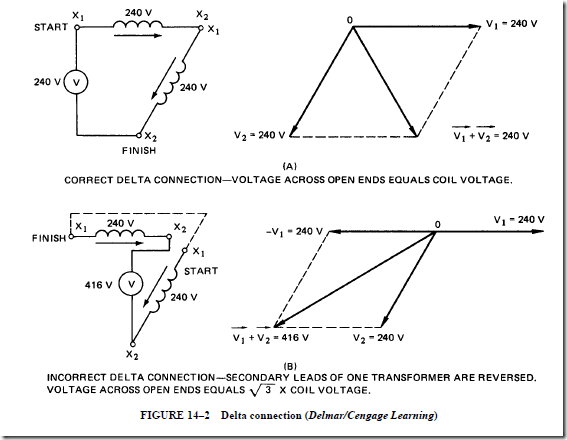
2. Connect the end of one secondary winding to the beginning of another secondary winding, as shown in Figure 14–2A. If the connection is correct, the voltage across
the open ends of the two transformers should be the same as the output of each transformer. In this case, the voltage is 240 V. The resultant voltage in the vector dia- gram is the same as the two secondary winding voltages and is equal to 240 V. Note that the path from start to finish is in the direction of both voltage arrows and does not cause a reversal of the vectors. The connections of the transformer windings are shown reversed in Figure 14–2B. The path from start to finish is in the direction of the voltage arrow and opposes the other voltage arrow. The V1 vector is reversed, and the resultant voltage is equal to M3 times the secondary coil voltage. The resultant voltage is 416 V. This condition is corrected by changing the connections of the secondary leads of one of the transformers. Thus, the new connections will be the same as in Figure 14–2A.
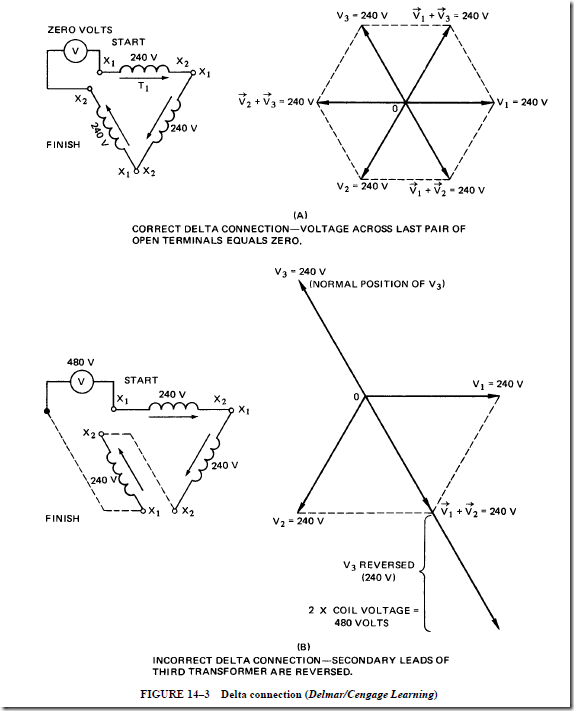
3. The proper connections are shown in Figure 14–3A for one end of the secondary coil of the third transformer. The vector diagram shows that there is a resultant voltage opposite to each secondary voltage and having a magnitude equal to the secondary voltage. Therefore, the voltage at any corner of the delta is zero. If the voltage is zero across the last pair of open leads, they can be connected together. A line wire is attached at each of the connection points. These three line wires form the 240-V, three-phase output. The three line voltages and each of the three transformer secondary voltages have the same value of 240 V. In Figure 14–3B the connections of the third secondary winding are reversed. As shown in the vector diagram, reversing the secondary voltage of the third transformer (V3) causes the resultant voltage to be twice the secondary voltage. In this case, the resultant voltage is 480 V. This condition is corrected by reversing the connections of the secondary leads of the third transformer. As a result, the voltage across the last pair of open leads is zero and the delta connection may be closed. (CAUTION: Never connect the last pair of open leads if there is a voltage difference across them. The potential difference must be zero, indicating that the winding connections are correct.)
Transformer Banks
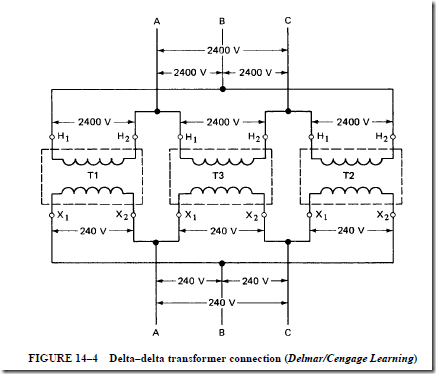
When the primary and secondary windings of three transformers are all connected in delta, the resulting arrangement is called a delta–delta (D–D) connection. The delta connection of the primary windings is indicated by the first delta symbol. The second delta symbol indicates the connection of the secondary windings. When two or three single- phase transformers are used to transform voltages on a three-phase system, they are known as a transformer bank.
The connections shown in Figure 14–4 are for a bank of transformers connected in delta–delta. Note that it is not necessary to represent delta–delta connections as triangles.
The delta–delta connection is used to supply an industrial load by stepping down a 2400-V, three-phase, three-wire service to a 240-V, three-phase, three-wire service. Assume that the industrial load consists of three-phase motors. The current in each wire is nearly the same and is considered to be balanced. For most applications, the load is balanced and the three single-phase transformers have the same kilovolt-ampere capacity. To determine the total capacity in kilovolt-amperes of the delta–delta-connected transformer bank, the three ratings are added. For example, if each transformer is rated at 50 kVA, the total capacity is 150 kVA.
The current–voltage relationships for a delta-connected circuit were described in Unit 10. The following information applies to both delta-connected circuits and systems.
1. In any delta connection, each transformer winding is connected across two line leads.
This means that the line voltage and the transformer coil winding voltage are the same.
2. The line current in a delta-connected transformer bank is equal to 1.73 times the coil winding current. In a closed-delta transformer connection, each line wire is fed by two transformer coil currents that are out of phase. Because the two coil currents are out of phase, they do not add together directly, but must be added vectorially to obtain the line current.
PROBLEM 1
Statement of the Problem
Three single-phase transformers are connected in delta–delta, as shown in Figure 14–4. Each transformer is rated at 50 kVA, 2400/240 V. The current in each of the three secondary line leads is 300 A. The secondary line voltage is 240 V across all three phases. The three- phase load connected to the transformer has a lagging power factor of 0.75. Determine
1. the kilovolt-ampere load on the transformer bank.
2. the kilowatt load on the transformer bank.
3. the percentage load on the transformer bank, in terms of its rated kVA capacity.
4. the current in each secondary winding.
5. the voltage across each secondary winding.
6. the kVA load on each transformer.
7. the line current on the primary side (assuming that the losses are negligible).
8. the kVA input to the transformer bank, if the losses are neglected.
Solution