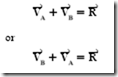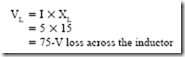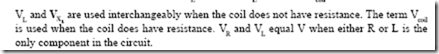Inductance in Alternating-Current Circuits : Vector addition and subtraction , Resistance and inductive reactance in series and Power and power factor.

VECTOR ADDITION AND SUBTRACTION

The use of vectors simplifies the analysis of circuit conditions. The student should have a basic working understanding of vector diagrams and how they can aid in the solution of circuit problems.

Many physical quantities, such as cubic inches, pounds, minutes, and degrees, are expressed in specific units. These quantities do not contain a direction. Such units of measurement are known as scalar quantities when using vector terminology. A scalar unit is defined in terms of its magnitude only. Many quantities relating to electric circuits do not have magnitude alone, but also have direction. Any quantity having both manitude and direction is called a vector. Examples of vectors include feet per second in a northeast direction, volts at 0°, and miles in a southerly direction. In electrical problems, rotating vectors are used to represent effective values of sinusoidal current and voltage in angular relationship to each other. According to convention, these vectors are rotated counterclockwise.

Basic Rules of Vectors

There are some basic rules of vector addition and subtraction that are used throughout the text. The student must understand these and other basic vector concepts before any attempt can be made to solve vector diagrams.

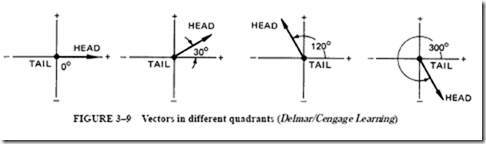
Figure 3–9 shows vectors of a unit length in different quadrants. Each vector is labeled to indicate the head and the tail. This notation will not be carried throughout the text.

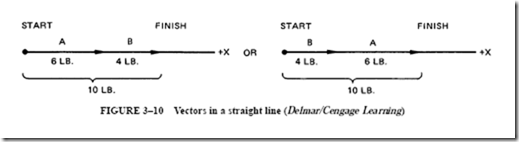
The following simple explanation of vector addition yields some basic rules that can be applied to more complicated problems. It is assumed that two people, A and B, exert a force of 6 lb and 4 lb, respectively, on a pole in the positive x direction. The total force exerted is 10 lb in the positive x direction. Figure 3–10 shows how these forces are arranged in a vector diagram. The relationship of these vectors is shown by the expression

The arrow above the V indicates a vector quantity. R is called the resultant of the two vectors. For this example, the resultant is 10 lb.

To add vectors, place the head of either vector to the tail of the other vector and measure or calculate the resultant from start to finish.

Applications of Vector Addition

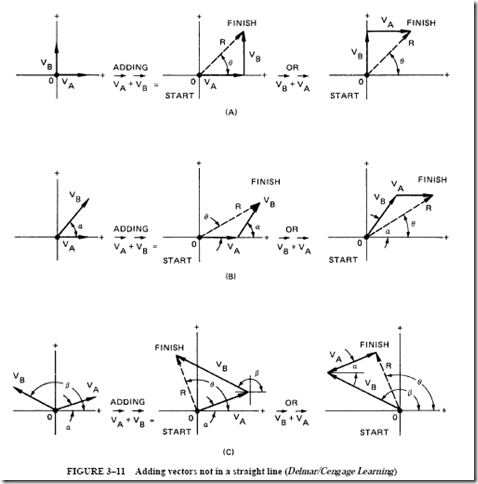
The basic rule of vector addition can be applied to vector combinations that are not in a straight line (Figure 3–11). For each part of Figure 3–11, vector V is added to vector V ,  or vector V A B is added to vector V .

For each of the diagrams, the angles are measured from the positive X axis. Angles  a and {3 in Figure 3–11C make the figure look more complicated than it really is.

The measurement of these angles ensures that vectors V and V are moved parallel to their original positions.

The addition of vectors in a straight line is the same as the arithmetic sum of their scalar values. Vectors that are not in a straight line require a geometric solution. Such vectors are not the sum of their scalar values.

Subtraction of Vectors

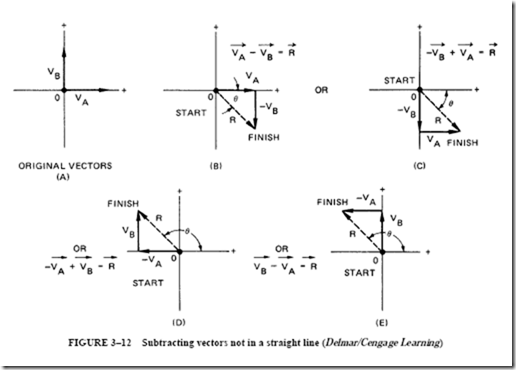
Examples of vector subtraction are shown in Figure 3–12. The vector to be subtracted is reversed and is then added head to tail to the remaining vector.

The resultants in Figure 3–12 are all equal in magnitude. However, the resultants in parts B and C of the figure differ in direction by 180° from the resultants in parts D and E. It can be said that their scalar values are equal but their directions are different.

The information presented in Unit 1 on angular relationships could just as well have used the term rotating vector (or phasor) in place of rotating line.

RESISTANCE AND INDUCTIVE REACTANCE IN SERIES

Unit 2 described circuits containing resistance only. The first part of this unit covered inductance, inductive reactance, and the voltage and current relationships in ac circuits containing inductance only. This background makes it possible to analyze more practical circuits containing resistance and inductive reactance in series.

To show the application of vector diagrams to ac circuits, two simple examples will be discussed. The first example is an ac circuit with a noninductive load, where the current and voltage are in phase. The second example is a circuit containing only inductance, with the current lagging behind the impressed voltage by 90°.

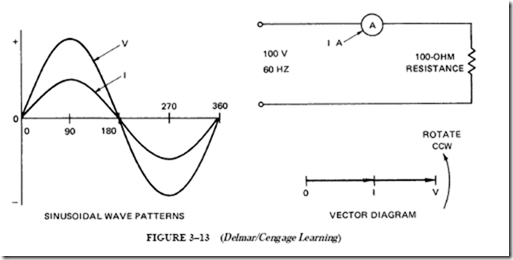
The circuit shown in Figure 3–13 was used in Unit 2. This circuit consists of a 100-0 noninductive heater unit with an effective line potential of 100 V. An effective cur- rent of one ampere is in phase with the voltage. The sine-wave patterns for the voltage and current for this circuit were developed in Unit 2. The student should recall that the first step was to determine the instantaneous voltage and current values at fixed increments in electrical time degrees. Then the sinusoidal wave patterns were plotted.

Diagrams for the Heater Current

The noninductive heater circuit has the sine-wave patterns shown in Figure 3–13. The vector diagram for this same circuit is also shown. The starting point of the vector diagram is marked “0.” The V and I vectors are assumed to rotate counterclockwise around point 0. Line V represents the effective line voltage of 100 V. This line is drawn to a convenient scale. Line I is the vector representing the current of one ampere. This vector is placed directly on the voltage vector to indicate that it is in phase with the voltage. The lengths of the vectors in vector diagrams represent effective values of current and voltage. (Note that I and V both begin at 0; V is not added to I and is shown as having a greater magnitude.)

Current is constant in a series circuit. Thus, all angles are measured with respect to the current vector, making it a reference vector.

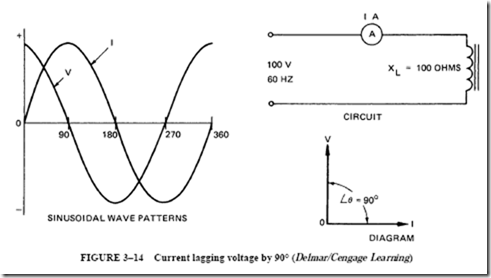
Earlier in this unit, an inductor coil was used to show the effect of inductive reactance (XL) of 100 0 and was connected across an effective potential of 100 V. The effective cur- rent for this circuit was one ampere. The current lagged the voltage by 90°. For this circuit, the inductive reactive circuit, the sinusoidal wave patterns for the voltage and current, and the vector diagram are shown in Figure 3–14.

Refer to the vector diagram in Figure 3–14. The line current is drawn horizontally from point 0. Because the voltage leads the current by 90 electrical time degrees, the volt- age vector must be drawn so that it is ahead of I by 90°. Vectors V and I are assumed to rotate counterclockwise. Thus, the voltage vector must point upward from 0. The angle between it and the current vector is 90°.

The angle by which the current lags behind the line voltage is called the phase angle or angle theta, abbreviated Lθ.

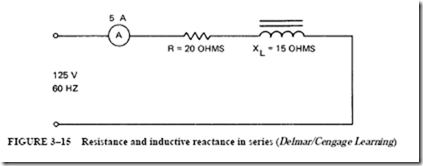
The series circuit shown in Figure 3–15 consists of a noninductive heater unit with a resistance of 20 0. The circuit also has an inductor coil with an inductive reactance (XL)

of 15 0. The coil is connected across a line potential of 125 V at a frequency of 60 Hz. The current in this circuit is limited in value by the resistance in ohms and the inductive reactance in ohms. Previously, it was shown that in a resistive circuit, the current is in phase with the voltage. In a circuit with inductive reactance, the current lags behind the voltage by 90°. There is both resistance and inductive reactance in the series circuit in Figure 3–15. For this circuit, the following quantities are to be found:

1. Voltage loss across the resistor

2. Voltage loss across the inductor coil

3. Line voltage

4. Impedance in ohms

5. True power in watts

6. Reactive power in VARs (volt-amperes-reactive)

7. Apparent power in volt-amperes

8. Power factor

Voltage Loss across R and X_L

The current in the circuit of Figure 3–15 is 5 A. Because this is a series circuit, the current is 5 A at all points in the series path. The voltage loss across the noninductive resistor will be in phase with the current. This loss is determined by using Ohm’s law as follows:

The voltage loss across the inductor coil leads the current by 90°. In other words, the current lags the voltage across the inductor coil by 90°. Ohm’s law is also used in this instance to determine the voltage loss across the inductor coil:

If the two voltage drops across the R and X components of the series circuit are added algebraically, the sum is 175 V. This value obviously does not represent the line voltage. The reason for this error is that the two voltage drops are 90 electrical degrees out of phase with each other. This means that the line voltage is the vector sum of the two voltage drops, or

Vector Diagram of a Series Circuit

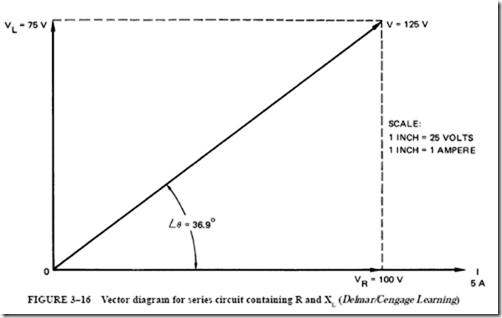
When a vector diagram is developed for a series circuit, it must be remembered that the current is the same at all points in the circuit. Therefore, the current is used as a reference line. In Figure 3–16, the 5-A current is drawn as a horizontal reference vector, using a workable scale.

The voltage loss across the resistance (V_R ) is placed on the current vector because both vectors are in phase. The voltage loss across the inductor coil is drawn in a vertical direction from point 0. This voltage (V_L ) leads the current by 90°. The resultant voltage is the vector sum of the two voltage drops, which are 90° out of phase.

The vector diagram shows that the line voltage is the hypotenuse of a right triangle. The hypotenuse of a right triangle is equal to the square root of the sum of the squares of the other two sides. Therefore, the line voltage for the series circuit is

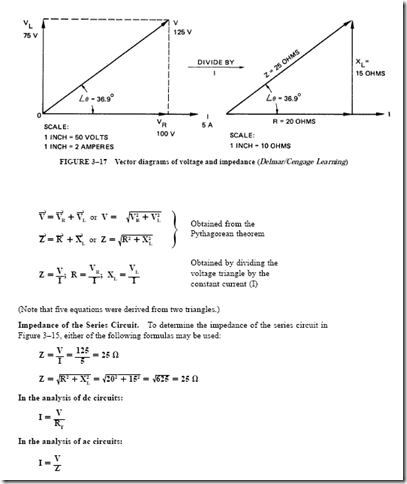
This voltage value can be checked against Figure 3–15 to ensure that it is equal to the line voltage. The 125-V line voltage causes a current of 5 A in the series circuit, which consists of resistance and inductive reactance. Each ohmic value limits the current. The combined effect of resistance and inductive reactance is called impedance and is represented by the letter Z.

Impedance is the resulting value in ohms of the combination of resistance and reactance.

The Impedance Triangle

A triangle known as an impedance triangle is obtained by dividing the voltage triangle by a constant reference vector I (Figure 3–17). Several equations can be written by inspecting the right triangles in Figure 3–17:

To find the line current in ac series circuits, Ohm’s law is used as follows:

POWER AND POWER FACTOR

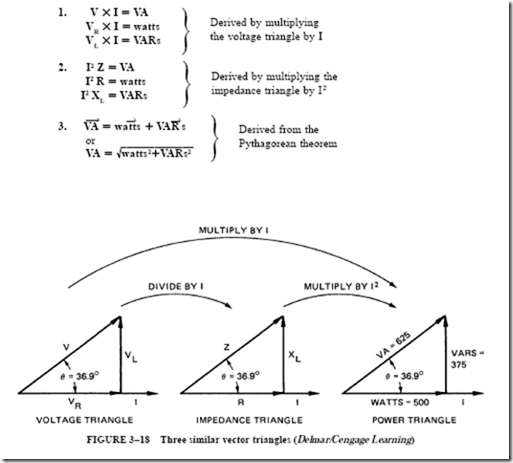
Several formulas for power can be written by inspecting the triangles in Figure 3–18. The impedance and voltage formulas were covered earlier in this unit.

By applying the basic principles of similar triangles and the Pythagorean theorem to the triangles in Figure 3–18, seven more formulas are derived. For the circuit of Figure 3–15, the apparent power, in volt-amperes, is

V X I = 125 X 5 = 625 volt-amperes

Determining True Power

In the noninductive circuit analyzed in Unit 2, the effective voltage and the effective current in amperes were in phase. The product of these values gave the power in watts taken by the circuit. The first part of the present unit deals with a circuit consisting of pure inductive reactance. In this circuit, the current lags the voltage by 90°. In a circuit with pure inductive reactance, the actual true power in watts is zero and is not the product of the volts and amperes. In a series circuit containing both inductive reactance and resistance (Figure 3–15), the current is neither in phase with the line voltage nor lagging 90° behind

the line voltage. The angle of lag for a circuit containing both R and X_L will be somewhere between these two limits. Power will be taken by the circuit.

How is the true power in watts determined? One way is to use the formula W = I2R. The actual power used in the resistance of any ac circuit is equal to the square of the effective current multiplied by the resistance in ohms.

Actual watts = I2 X R = 52 X 20 = 500 W used in the resistance of  the circuit in Figure 3–15  The power taken by this circuit can also be found by multiplying the voltage loss across the resistance section of the circuit by the current. Because the current and voltage are in phase, their product is the true average power:

Watts = V_R X I = 100 X 5 =500 W used in the resistance of the circuit

Note that the true power in watts is the same using either method. Recall from Direct Current Fundamentals that electricity is a form of pure energy. Watts is a measure of the amount of electrical energy converted to some other form. When current flows through the resistive part of any circuit, electrical energy is converted into thermal energy in the form of heat.

Reactive Power

In addition to the true power used in the resistance, there is another power component to be considered. This component is called reactive power and is expressed in a unit called volt-amperes-reactive. This unit is usually shown in the abbreviated form “VARs.” It rep- resents the product of volts and amperes that are 90° out of phase with each other.

Figure 3–8 shows a graph of reactive power over one cycle. The total net true power in watts is zero for one cycle because the two negative power pulses cancel the two positive power pulses. As a result, the descriptive term wattless power is sometimes applied to this power component in an ac circuit. The correct terminology for this power component is quadrature power or reactive power. In the series circuit in Figure 3–15, the voltage drop across the component with pure inductive reactance is 75 V. Therefore, the quadrature power in VARs is the product of the voltage across the reactance and

the current. These values are 90° out of phase. This quadrature, reactive, or wattless power is

VARs = V_L X I = 75 X 5 = 375 VARs

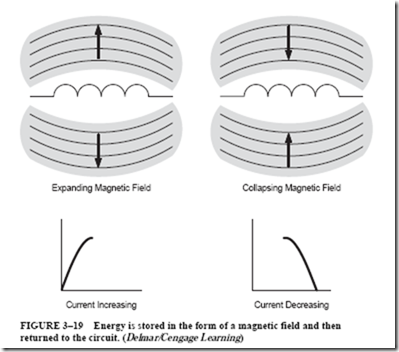
To better understand wattless power or VARs, consider that true power or watts can be produced only when electrical energy is converted to some other form. When the alternating-current waveform flowing through an inductor increases in value, it causes a magnetic field to be produced around the inductor (Figure 3–19). Energy is required to create or establish the magnetic field. When the alternating-current wave- form begins to decrease in value, the field collapses and returns the energy to the circuit. In the case of an inductor, electrical energy is stored in the form of a magnetic field and then returned to the circuit. The electrical energy is not changed to some other form.

The true power in watts is used in the resistance of the circuit. The quadrature power is identified with the reactance of the circuit. The combination of the two power components yields a resultant called the apparent power in volt-amperes. This resultant in volt-amperes can be regarded as the hypotenuse of a power triangle, as shown in Figure 3–18.

Power Factor

Power factor (PF) is defined as the ratio between the true power in watts and the apparent power in volt-amperes. The power factor may be expressed as a decimal value or as a percentage:

Unit 4 will present a thorough study of alternating-current resistance. This quantity is more properly called effective resistance. More realistic series circuits consisting of resistance and impedance components will be analyzed using the formulas derived in this unit.

SUMMARY

• The induced voltage of a conductor, coil, or circuit is caused by a changing magnetic field cutting across the circuit components. This voltage is proportional to the rate of change of the lines of force.

• In a dc circuit, the inductive effect stops once the current reaches the value defined by Ohm’s law and remains constant.

• Lenz’s law states that in all cases of electromagnetic induction, the induced voltage and the resultant current are in a direction that opposes the effect that produces them.

• Induction in an electrical circuit can be called electrical inertia.

• In a circuit containing inductance, current will increase at a much slower rate toward a maximum value than it does in a circuit containing resistance only.

• The length of time required for the current to decay to zero, once the circuit is deenergized, equals the time required for the current to rise to its Ohm’s law value when the inductive circuit is energized.

• Inductance is the ability of a circuit component, such as a reactor coil, to store energy in the electromagnetic field.

• The unit of inductance is the henry. A circuit or circuit component is said to have an inductance of one henry when a current change of one ampere per second induces a voltage of one volt.

• In an ac circuit with the same effective voltage as an equivalent dc circuit, the circuit current will be less than in the dc circuit because of the choking effect of inductance in the ac circuit.

• The induced voltage or counterelectromagnetic voltage in a series inductive circuit opposes the impressed voltage and thus limits the circuit current.

• Removing the laminated iron core from a coil in an ac circuit will decrease the inductive reactance in the circuit. In effect, the circuit current is increased.

• Increasing the frequency of an ac inductive series circuit decreases the circuit current.

• Inductance in an ac circuit is just as effective in limiting current as resistance.

• Inductive reactance is the opposition in an ac circuit due to inductance.

where w is the Greek letter omega and represents angular velocity; 2’ITf also is equal to angular velocity.

4. An accepted value for 2’ITf is 377, when the frequency is 60 Hz. For 25 Hz, 2’ITf = 157.

5. Ohm’s law for inductive reactance is

• The angle by which the current lags behind the line voltage is called the phase angle or

angle theta, abbreviated L8.

1. In a` pure inductive circuit, the current lags the voltage by 90°.

2. In a circuit containing both resistance and inductive reactance, the angle of lag is less than 90° and is equal to the vectorial sum of both the X components.

• A scalar is a measure of a specific unit of quantity [such as 6 inches (in.) or 5 pounds (lb)]. It has magnitude but does not show any direction.

• A vector is any quantity having both magnitude and direction.

• According to convention, vectors are rotated counterclockwise.

• To add vectors, place the head of either vector to the tail of the other vector and measure or calculate the resultant from start to finish.

1. Vectors in a straight line can be added by taking the arithmetic sum of their scalar values.

2. Vectors not in a straight line require a geometric solution and are not the sum of their scalar values.

• To subtract vectors, the vector to be subtracted is reversed and is then added head to tail to the remaining vector.

• All angles are measured with respect to the current vector as the reference vector, because current is constant in a series circuit.

• The actual power (true power) in watts taken by a pure inductive circuit is zero.

1. The two positive pulses of power (when power is taken from the supply) are equal to the two negative pulses of power (when power is returned to the supply from the magnetic field). The net power taken by the inductor coil in one complete cycle is zero.

2. True power is equal to I2 R.

[Note: The product of the effective voltage and the effective current may not equal the power in watts in any circuit containing inductive reactance.]

Achievement Review

1. State Lenz’s law.

2. Define the standard unit of measurement of inductance.

3. What is meant by inductive reactance?

4. Add the following vectors (show the vector diagram for each addition):

a. 208 V at 90° and 120 V at 180°

b. 50 V at 0° and 42.1 V at 270°

c. 20.3 V at 0° and 8.2 V at 0°

d. 46.2 V at 0°, 71.4 V at 90°, and 38 V at 0°

5. Subtract the following vectors (show the vector diagram for each subtraction):

a. 208 V at 90° from 120 V at 180°

b. 50 V at 0° from 42.1 V at 270°

c. 20.3 V at 0° from 8.2 V at 0°

d. 84.2 V at 0° from 71.4 V at 90°

6. Resolve a voltage of 48 V into two coordinates, one of which is 23.2 V.

7. A line voltage (V) of 100 V is at an angle of 45° with respect to the line current. Find the horizontal component (V ) and the vertical component (V ) of the applied voltage.

8. An inductor coil with an inductance of 0.5 H and negligible resistance is connected across the terminals of a 230-V, 60-Hz supply.

a. Determine the current in amperes taken by the inductor coil.

b. What power in watts is taken by this inductor coil if the current lags the impressed voltage by 90 electrical degrees?

9. a. If the inductor coil in question 8 is connected across the terminals of a 230-V, 25-Hz supply, what is the current in amperes?

b. Explain the reason for any change in current as the frequency changes.

10. An inductor coil connected across a 120-V, 60-Hz supply takes 10 A. The resistance of the inductor coil can be neglected. Determine

a. the inductive reactance of the coil.

b. the inductance of the coil.

11. An ac motor takes 10 A when connected across a 240-V, 60-Hz source. A wattmeter connected in the circuit reads 1500 W. Determine

a. the power factor of the motor.

b. the angle of lag of the current behind the voltage for the motor circuit.

12. An industrial load connected to a 440-V, 60-Hz line takes 50 A. The current lags the voltage by 30 electrical degrees.

a. What is the power factor of this circuit?

b. Determine

1. the apparent power, in volt-amperes.

2. the true power, in watts.

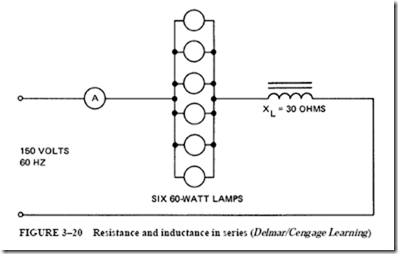
13. A series circuit (Figure 3–20) consists of resistance and inductive reactance connected in series across a 150-V, 60-Hz source. The resistance component of the series circuit consists of six 60-W, 120-V lamps, connected in parallel. Each lamp has a hot resistance of 240 0. The inductive reactive part of the series circuit consists of an inductor coil with an inductive reactance of 30 0 and negligible resistance. Determine

a. the impedance of the series circuit.

b. the current, in amperes.

c. the inductance of the inductor coil, in henrys.

 

14. For the circuit in question 13, determine

a. the voltage loss across the bank of lamps.

b. the voltage drop across the inductor coil.

c. the true power in watts taken by the circuit.

d. the reactive power in VARs taken by the circuit.

15. a. For the circuit in question 13, determine the power factor.

b. What is the angle of lag or the power factor angle?

16. The following diagrams are to be drawn to scale for the circuit in question 13:

a. A voltage vector diagram

b. An impedance triangle

c. A triangle of power components

17. A 30-0 resistor and a reactor coil (inductor coil) with a 0.2-H inductance and negligible resistance are connected in series across a 120-V, 25-Hz supply. Determine

a. the impedance of the circuit.

b. the current.

c. the true power in watts taken by the circuit.

d. the power factor.

e. the phase angle.

18. Draw a vector diagram for the circuit in question 17. The vectors must be drawn accurately to a convenient scale. Mark each vector with the proper letter identification.

19. A reactor coil that has negligible resistance is connected in series with a group of incandescent lamps connected in parallel. The purpose of the reactor coil is to reduce the voltage across the lamps. When the circuit is energized from a 120-V, 60-Hz source, the current in the reactor coil is 25 A. The voltage across the lamps is 30 V. Determine

a. the circuit impedance, in ohms.

b. the voltage loss across the reactor coil.

c. the inductive reactance of the inductor coil, in ohms.

d. the inductance of the reactor coil, in henrys.

e. the power factor and the angle of lag.

20. Using the circuit given in question 19

a. determine the power in watts used in the circuit.

b. determine the quadrature, or vertical power component, in VARs.

c. determine the apparent power, in volt-amperes.

d. draw an impedance triangle and a power triangle to scale.

e. draw a voltage vector diagram to scale.