21–8 SPEED CONTROL OF DC MOTORS
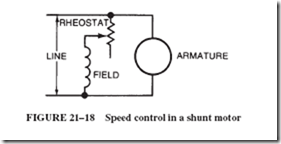
Not all electric motors are suited to have their speed controlled with smooth acceleration or deceleration. DC motors do have this ability. Speed is easily controlled in shunt motors by placing a rheostat in series with the shunt field, thereby varying the current and, consequently, the flux, as shown in Figure 21–18.
Many students of electricity make the wrong assumption that increased resistance will slow the motor. This is not so; just the opposite will occur. When the resistance is increased, the current and therefore the magnetic flux are decreased; thus, the motor speeds up. This happens because a reduction in flux will reduce the cemf, which in turn increases the armature current. As we have seen earlier, these events lead to increased torque and increased speed. Our shorthand notation would describe this chain of events as follows:
Needless to say, the opposite actions occur when the field resistance is decreased.
It would also be possible to vary the speed of the motor by adding a rheostat into the armature circuit. This, however, is not a desirable practice because armature circuits generally draw a lot of current and the resulting I2R losses would be prohibitively large. This also results in poorer speed regulation.
The term normal speed refers to the speed of the motor without any speed control mechanism in place and full voltage across the field and armature.
We have already seen that added resistance in the shunt circuit will result in above-normal speed. There are occasions, however, when a motor must be operated at below-normal speed, at which time it becomes necessary to insert resistance into the armature circuit. This may not be a happy solution to the problem, but it surely reduces the speed by decreasing the armature current. In this respect, there is no difference between the shunt motor and the compound motor.
Note: The practical and preferred way to vary the speed of a DC motor is by varying the resistance in the shunt field circuit.
Unfortunately, like everything else in life, this method presents us with mixed blessings. In other words, controlling speed by varying the field’s magnetic strength has some drawbacks, too. With the reduction of magnetic flux, there is a corresponding reduction in the production of torque. This means that a desired speed increase brings with it a reduction in torque.
In this respect, armature control appears to be superior. In order to speed up the motor, we would increase the current through the armature (by varying a rheostat). The motor reacts to limit the current increase by speeding up and producing more counter-emf. Since the strength of the magnetic field remains unchanged, the torque will not suffer.
On the other hand, rheostats in the armature circuit would have to be unreason- ably large to handle the armature current. As mentioned before, the resulting I2R losses would be costly, and the efficiency and speed regulation of the motor would suffer. A solution of this dilemma would call for armature control without rheostats. This innovation came about with the introduction of electronic devices known as thyristors.
Electronic Speed Control
The rapid development of solid-state devices during the last few decades has brought about some extraordinary changes in the control of electric power. Semiconductor devices, known as thyristors, can control vast amounts of power with only very small amounts of
input power. Such devices have ushered in a new era of industrial electronics, aimed at the control of electrical power and machines.
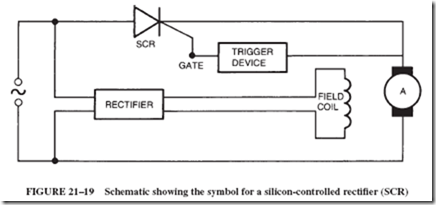
The silicon-controlled rectifier (SCR) is the most popular device among the thyristors. Thyristors can be defined as electronic switches. The SCR can be switched rapidly, thousands of times per second, without any moving parts. The schematic symbol of the SCR is shown in Figure 21–19, where it is shown connected, like a switch, in series with the armature of a shunt motor. An electrical pulse at the gate will trigger the device into its on position.
You may have already noticed that the DC motor is shown connected to an AC source. In spite of this, the motor does operate on DC. The field receives DC from a bridge rectifier, and the armature receives rectified DC from the SCR. In addition to providing rectification, the SCR controls the average armature voltage and current by pulsing the current through the armature in response to the trigger pulses received by the gate. This action, in turn, controls the speed of the motor. The trigger pulses at the gate are regulated by special electronic circuits, thereby controlling the amount of energy delivered to the motor.
As you progress in your studies of electronics, you will encounter such devices time and again, and you will then have to study their principles of operation. For the time being, it will suffice for you to realize that such electronic devices and techniques have invaded the domain of industrial electricity, and that electronic devices, such as the SCR, will be used increasingly to replace rheostats in the use of motor control.
21–9 REVERSAL OF ROTATION
If you recall that torque in an electric motor depends on the interaction of two magnetic fields, you may easily understand that the direction of rotation depends on the magnetic polarity these fields have with respect to each other.
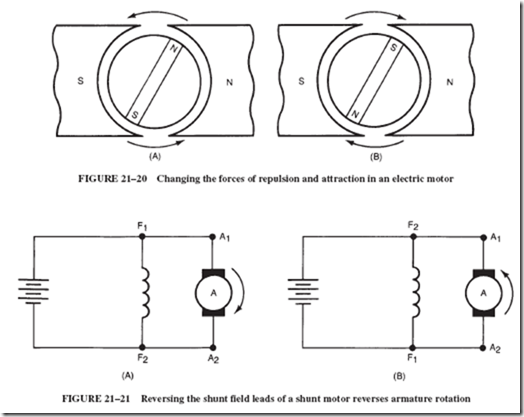
Figure 21–20 illustrates that the forces of repulsion and attraction can be changed by reversing the polarity of the armature with respect to the polarity of the field coils, and vice versa. This will also explain why it is generally not possible to affect reversal
simply by changing the leads of the power source. This technique works only with motors in which the field is provided by permanent magnets, or permanent-magnet (PM) motors. Small, electric toy motors are generally of this kind and can be easily reversed by merely switching the power leads.
By contrast, all motors with electromagnetic fields can be reversed by changing the leads of their field winding. When this is done, the armature leads remain unchanged. Remember, motor reversal is achieved by switching either the field winding or the armature leads, but not both. The wires leading to the armature are generally labeled A1 and A2, and the terminals of the shunt field are marked F1 and F2. Let us assume that a given motor is turning clockwise when its A1 terminal is connected to F1 and A2 is connected to F2; see Figure 21–21A. If it should become necessary to change the direction of rotation, it is only necessary to reconnect the wires A1 to F2 and A2 to F1; see Figure 21–21B.
When compound motors are to be reversed, it is best to switch just the connections
to the armature. If the design of the machine makes it easier to change the field coils, it must be remembered to change both the shunt and the series field. (The terminals of the
series fields are labeled S1 and S2.) If only one of the two field windings were switched around, the motor would change its characteristic of a cumulative compound motor to that of a differentially compounded machine, or vice versa.
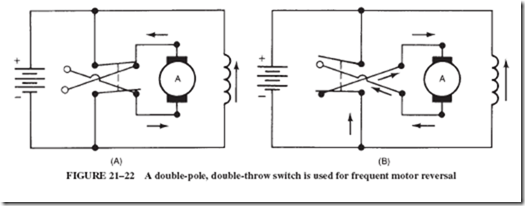
When frequent reversal of a motor is desired, the installation of a double-pole, double-throw (DPDT) switch will facilitate the task. Figure 21–22 shows how the switch changes the direction of the current through the armature and, consequently, the direction of the motor.
Determining the Direction of Rotation of a DC Motor
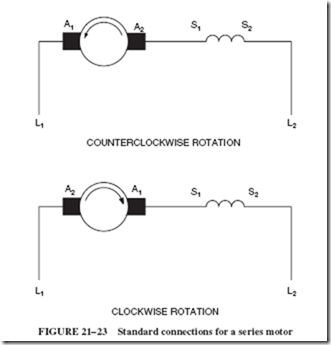
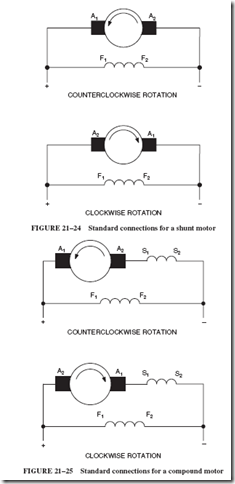
The direction of rotation of a DC motor is determined by facing the commutator end of the motor. This is generally the back or rear of the motor. If the windings have been labeled in a standard manner, it is possible to determine the direction of rotation when the motor is connected. Figure 21–23 illustrates the standard connections for a series motor. The standard connections for a shunt motor are illustrated in Figure 21–24, and those for a compound motor in Figure 21–25.
The direction of rotation of a DC motor can be reversed by changing the connections of either the armature or the field leads. It is common practice to change the armature leads, to prevent changing a cumulative compound motor into a differential compound motor. However, if a motor contains only a shunt field, there is no danger of changing the motor from a cumulative to a differential compound motor. Thus the shunt field lead connections are often changed on small motors because the amount of current flow through the field is much less than the current flow through the armature.
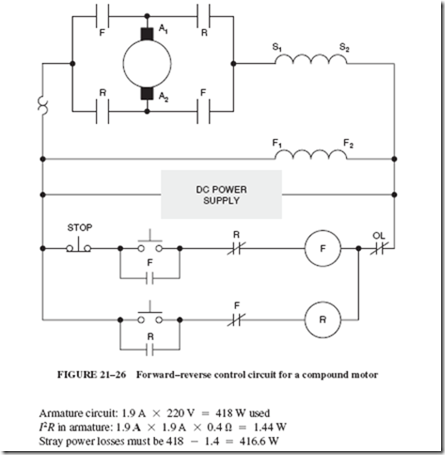
Large compound motors often use a control circuit, as shown in Figure 21–26, that uses magnetic contactors to reverse the flow of current through the armature. If we trace the circuit, we see that when the forward or reverse direction is chosen, only the current through the armature changes direction. The current flow through the shunt and series fields remains the same.
21–10 POWER LOSSES
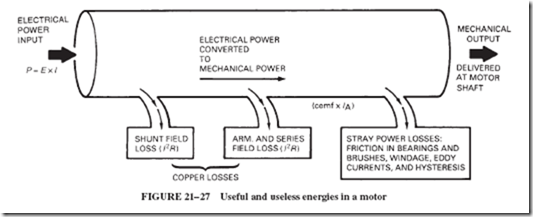
Power losses in electric motors are classified, just as they were for generators, as I2R losses and stray power losses. This was explained in Section 19–9, which you may want to review at this time. The drawing used in conjunction with that explanation is similar to Figure 21–27, which illustrates the relationship between useful and useless energies in a motor.
The drawing presents an analogy between a machine and a conduit, both of which have an input on one side and an output on the other. The conduit has some leaks through which various losses are incurred, thereby causing the output to be less than the input. This ratio of output to input is, of course, known as efficiency. This, too, may be reviewed in Section 19–9.
EXAMPLE 21–4
Given: A shunt motor with a 200-ohm field and a 0.4-ohm armature. At no load, the motor takes 3 amperes on a 220-volt line.
Find: The stray power losses.
Solution
21–11 PERMANENT-MAGNET MOTORS
Up to this point we have discussed the three types of DC motors with electromagnetic field coils: shunt, series, and compound motors. These motors have been the traditional workhorses of industry wherever the specifications called for variable load or speed applications (or both).
Naturally, the field coils can be replaced with permanent magnets, thereby creating a permanent-magnet, or PM, motor. For many decades PM motors have had limited applications. They were often used for powering electrical toys and for various applications in automobiles, such as windshield wipers and window lifts. This trend has now been reversed as a consequence of new, sophisticated developments in electronics, as well as improved design of rare-earth and ceramic magnets. As a result, the PM motor has become a favorite in high-technology applications involving motion control, such as robotics.
PM motors can be broadly classified as being either
1. Brush-type PM motors (mechanically commutated)
2. Brushless PM motors (electronically commutated)
Of these categories, the brush-type PM motor is the prevalent one, although this trend may change as the cost of electronic commutation circuits further decreases.
Brush-Type PM Motors
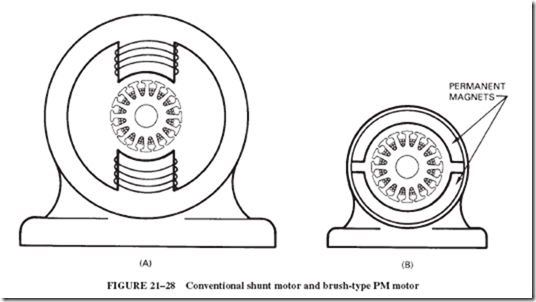
As previously stated, the key feature that distinguishes the PM motor from a shunt motor is the replacement of the shunt field winding with permanent magnets.
Figure 21–28 is meant to convey the idea that for any given horsepower rating the PM motor can be made much smaller in size and weight. This is one of the advantages of PM motors, which derives from the fact that heat losses of the field coils have been eliminated, lessening the need for ventilation. The reduction of electrical losses also makes the PM motor somewhat more energy efficient.
The brush-type PM motor uses the same commutation arrangement you have come to know in conventional wire-wound field motors. In other words, current is carried to the armature by a pair of spring- loaded carbon brushes that ride on the commutator. Recall that if the armature had a single winding only, it would rotate only until the magnetic fields reach an equilibrium position. To achieve continuous motion, the armature has multiple windings, which are sequentially energized and de-energized through the brush and commutator assembly. Thus a nearly constant force of magnetic attraction and repulsion between the armature and the field sustains the rotary motion and torque output.
You will remember that motor performance is described in terms of rotational speed and torque output. The horsepower output derived from a motor is directly proportional to the product of speed and torque, or, mathematically speaking:
Php = N x Torque x rpm
Compare this with the equation shown under the heading “Calculation of Horsepower” in Chapter 20, which has been simplified here to show that the torque output is expected to increase whenever speed decreases.
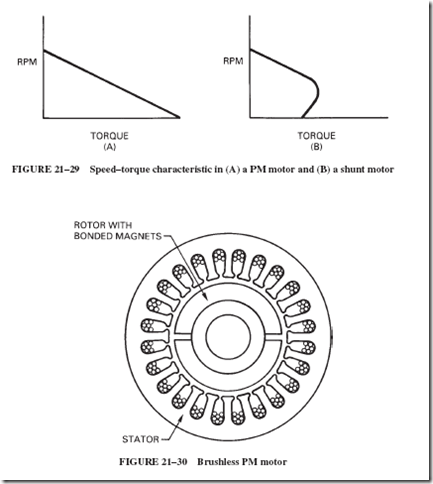
This expectation is more fully realized with permanent-magnet motors than with electro- magnetic motors (those with field windings). PM motors are said to have a more linear speed–torque characteristic. This is shown by comparison of Figures 21–29A and 21–29B. The linear characteristic of the PM motors occurs because armature reaction within them is virtually eliminated. This makes for predictable performance in high-technology
applications such as robotics, where precise motion control is very important.
Brushless PM Motors
Advanced electronic technology gave rise to the development of the brushless PM motor, in which the conventional commutator and brush assembly is replaced by a complex electronic commutation system. This calls for radical design changes. The armature and the PM field have their positions interchanged. That is to say, the armature winding is no longer rotating, but is mounted within the outer frame structure, and is now called the stator. Consequently, the permanent magnets are mounted on the revolving structure of the motor, which is now referred to as the rotor, as shown in Figure 21–30.
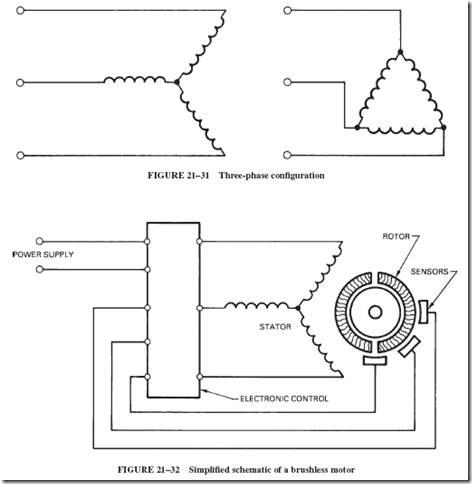
The coils of the stationary armature, or stator, are generally arranged in a three-phase configuration. The term three-phase is generally associated with alternating current (AC) and implies the use of three-coil windings as shown in Figure 21–31.
Recall that in conventional motors the armature windings are sequentially turned on and off by making or breaking contact with pairs of commutator segments, thereby assuring the correct relationship between the field flux and the armature flux. In a brushless motor, this critical relationship is maintained by electronic sensors that monitor the position of the revolving PM field with respect to the stationary armature. They generate a feedback signal that
is applied to appropriate control circuits, which then deliver current sequentially to the stationary armature. A nearly constant spatial relationship is maintained between the magnetic fields of the stator and the rotor, thereby developing the desired torque; see Figure 21–32.
The operating characteristics of brushless PM motors are similar to those of brush-type PM motors. That is to say, they have a high starting torque and maintain a linear torque-to- speed relationship over their full range of operation.
It is noteworthy that the maximum torque obtainable from a DC motor is limited by commutation rather than by heating. If the armature current becomes excessive, severe arcing may ruin the brushes and commutator. In spite of this limitation, brush-type PM motors are more widely sold than brushless PM motors, mainly because of their lower cost.
However, brushless PM motors have become very popular for variable-speed applications such as air handlers found in the air-conditioning field. The speed of the brush- less PM motor can be controlled by changing the frequency of the three-phase power applied to the stator field. The electronic controls necessary for making this conversion are generally located inside the motor housing, as shown in Figure 21–33.
As stated earlier, these desirable characteristics make PM motors strong contenders in the market for fractional horsepower motors that provide precise motion control.
SUMMARY
• The left-hand rule applies to generators, while the right-hand rule applies to motors.
• Torque is proportional to flux and armature current. Increase of either increases torque.
• Counter-emf is proportional to flux and rpm. Increase of either increases emf.
• The amount of counter-emf determines the useful mechanical output from the motor.
• Armature windings of motors are similar to those of generators. Lap windings are suit- able for high-current applications, while wave windings sacrifice current for high- voltage applications.
• In motors, the interpoles have the same polarity as the main pole directly in back of them (with respect to the direction of rotation). This is opposite to the placement of interpoles in generators.
• The shunt motor has its field coils in parallel with the armature. Its constant field strength limits input current and speed at no load.
• A shunt motor accelerates to excessive speeds when the shunt field is lost.
• The series motor has its field coil in series with the armature. At no load, reduced field permits enough current to produce torque that accelerates the motor greatly. At heavy load, the torque is high, the speed is low.
• A series motor accelerates to excessive speeds when the load is lost.
• When the advantages of series and shunt motors are compared, it is seen that the shunt motor has the more constant speed, but a series motor of the same horsepower rating can exert a much greater torque, when necessary, without a large increase in current.
• Compound motors have both series and shunt fields. The relative ampere-turns of the two fields determine the speed and torque characteristics of the motor.
• Generally, compound motors are cumulatively compounded and long-shunt connected.
• Weakening the field speeds up the shunt motor; reduced armature current slows the shunt motor.
• Speed control can be achieved by either changing the current in the field or in the armature.
• When rheostats are used for speed control, the preferred placement of the rheostat is in the shunt field circuit.
• Armature control is the preferred method when electronic components are used to vary the speed.
Achievement Review
1. An armature, resistance 0.47 ohm, is supplied with 124 volts DC and 40 amperes. Calculate
a. The volts used to overcome the resistance of the armature
b. The volts used to make mechanical energy (counter-emf)
c. The horsepower output
d. The efficiency
e. The watts heating rate
2. Calculate the current in the armature of question 1 if the armature stalled because of overload.
3. Determine the direction of the rotation of the armatures shown in Figures 21–4 and 21–7.
4. What is the polarity of interpoles in reference to the polarity of main field poles in a direct current motor?
5. a. Show with characteristic curves the speed and torque performance for a shunt motor.
b. List four industrial applications for a shunt motor.
6. a. Show with characteristic curves the speed and torque performances for a series motor.
b. List four industrial applications for a series motor.
7. a. Show with characteristic curves the speed and torque performance for a cumulative compound motor.
b. List four industrial applications for a cumulative compound motor.
8. A shunt motor is required to carry an additional load. List the sequence of steps showing how this motor adjusts itself to carry the additional load.
9. The armature of a DC shunt motor carries 15 amperes. The resistance of the armature circuit is
0.7 ohm. The line voltage is 220 volts.
a. Find the counter-emf generated in the armature.
b. Find the power output in watts.
c. Find the power output in horsepower.
10. A 3-horsepower, 120-volt shunt motor takes 23 amperes at full load and 3 amperes at no load. Shunt resistance is 150 ohms; armature resistance is 0.25 ohm; and no-load speed is 1,600 rpm. Find
a. Counter-emf at no load
b. Counter-emf at full load
c. Full-load speed
d. Percentage speed regulation
11. Explain the meaning of the following terms:
a. Speed regulation
b. Speed control
12. Explain what happens under each of the following conditions:
a. The load is removed from a series motor.
b. Resistance is added to the armature circuit of a shunt motor.
c. The rheostat in series with the shunt field of a shunt motor operating at no load becomes open-circuited.
d. The field rheostat in series with the shunt field of a shunt motor is adjusted so that all the resistance of the rheostat is cut out and the shunt field current increases.
13. a. Itemize the losses that reduce the efficiency of a motor, and state in what parts of the motor each loss occurs.
b. State which of these losses are constant and independent of the load.
c. When the constant losses are groups together, what term is used?
14. A motor with an input of 1,000 watts delivers an output of 1 horsepower. If the copper losses are 134 watts, what are the constant or fixed losses, which are independent of the load?
15. A 50-horsepower, 220-volt shunt motor has a full-load efficiency of 83%. Field resistance is 110 ohms; armature resistance is 0.08 ohm. At full load, determine
a. Total power input in watts
b. Line current
c. Total copper losses
d. Stray power losses
16. A DC shunt motor takes 40 amperes at full load when connected to a 115-volt line. At no load, the motor takes 4.4 amperes. Shunt field resistance is 57.5 ohms; armature circuit resistance is 0.25 ohm; full-load speed is 1,740 rpm.
Find
a. Stray power loss
b. Copper loss at full load
c. Efficiency at full load
d. Horsepower output at full load
17. The generator of a motor–generator set is delivering its full-load output of 10 kilowatts. The generator has an efficiency of 88.5%; the motor operates on a 230-volt line. Determine
a. The output of the motor in horsepower
b. The number of amperes the motor is taking from the line when the generator is delivering at rated load (The overall efficiency of the motor–generator set is 85%.)
18. A motor operating on a 120-volt DC supply drives a direct current generator, which is delivering 1 kilowatt at 240 volts. Under these conditions the motor has 78% efficiency and the generator has 85% efficiency. Determine
a. The output of the motor in horsepower
b. The line current drawn by the motor
19. A 220-volt, 20-horsepower compound motor (long shunt, Figure 21–16A) has an armature resistance of 0.25 ohm, series field resistance of 0.19 ohm, and shunt field resistance of 33 ohms.
a. Calculate the current taken by the motor at the instant of starting if it is connected directly to the 220-volt line.
b. Calculate the current when the motor is running if the armature is developing 184 volts counter-emf.
20. Complete the external and internal connections for the shunt motor in the accompanying sketch for counterclockwise rotation. The interpole field windings are to be a part of the armature circuit, which terminates at the connection points marked A1 and A2. Be sure to have the proper connections for the interpole field windings and the main field windings so that their polarities are correct for counterclockwise rotation.