18–4 LENZ’S LAW
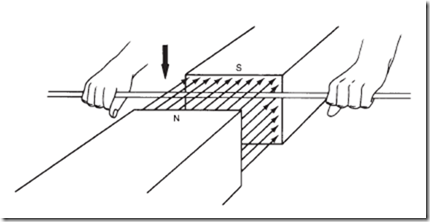
There is a more fundamental way of determining the current direction. As pointed out before, electrical energy is produced by mechanical energy; the hand that removes the magnet from the coil must do some work. The magnet does not push out of the coil by itself; the hand must pull it out.
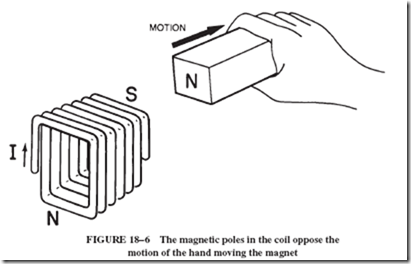
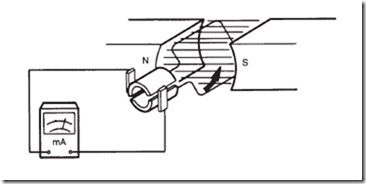
The coil itself, however, makes it difficult to move the magnet. It creates magnetic poles of its own that oppose the motion of the hand. Figure 18–6 shows the magnet a little more removed from the coil than in Figure 18–5. The induced current in the coil is in such a direction as to develop poles in the coil as shown. (Recall the left-hand rule for a coil.) The attraction of these opposite poles pulls the magnet toward the coil.
If the motion of the magnet is reversed, that is, pushed into the coil, the induced current reverses also, developing poles on the coil that repel the approaching magnet.
This general idea was recognized years ago by Heinrich Lenz and is summarized in Lenz’s law:
An induced voltage or current opposes the motion that causes it.
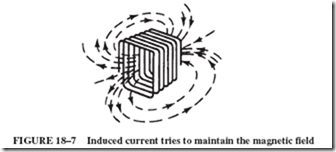
Lenz’s law is also useful in determining induced current direction in more complex machinery. Note that in Figures 18–3 and 18–5 the coil is surrounded by the magnetic field of the bar magnet. Removing the magnet removes this magnetic field. The induced current in the coil tries to maintain a field of the same strength and direction as the field
that is being removed; see Figure 18–7. (Apply the left-hand rule to the coil in Figure 18–6 to determine direction and shape of the field of the coil due to current in it.)
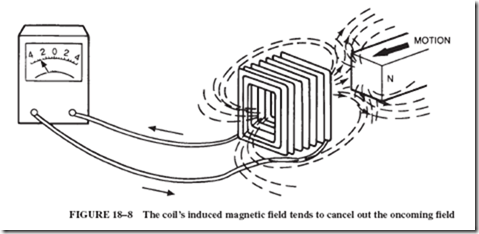
There is another way of looking at Lenz’s law. Originally, the coil in Figure 18–8 had no magnetic field in it. As the approaching magnet’s lines of force enter the coil, the coil develops a field of its own that tends to restore conditions in the coil to the original zero-field condition, that is, tends to cancel out the oncoming field. Therefore, there is an alternate way of stating Lenz’s law:
An induced voltage or current opposes a change of magnetic field.
In the preceding discussion, the terms induced voltage and induced current seem to have been used interchangeably. One should understand that the relative motion of wire and magnetic field always induces a voltage, or emf. If there is a closed circuit, this induced emf causes a current.
18–5 INDUCTION IN ROTATING MACHINES
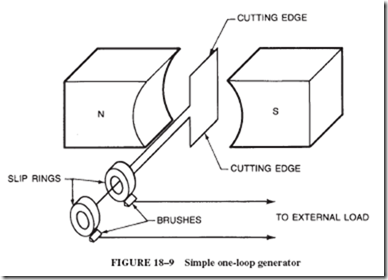
Commercial generators produce electrical energy either by rotating coils of wire in a stationary magnetic field or by rotating a magnet inside a stationary coil of wire. Let us explore the rotation of a coil within a magnetic field. To analyze this action, we are going to reduce the coil to one single loop and examine the result of its rotation for one revolution. The single loop shown in Figure 18–9 represents the concept of such a simple generator.
Mechanical energy must be expended to rotate this coil within the magnetic field and cut the lines of flux. In practical applications, such energy is provided by turbines or engines called prime movers.
As the coil is rotated, an emf is induced, which appears between the two ends of the loop. Two metal bands, called slip rings, are attached to these ends to facilitate the transfer of this voltage to an external load. Carbon brushes riding on these smooth metal rings conduct the generated electricity to the circuit, where it can be utilized.
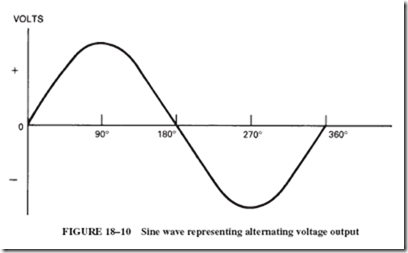
The voltage generated in this manner continually changes in magnitude and direction. Such emf is known as alternating voltage and can be made visible on an instrument known as the oscilloscope. The pattern displayed is called a sine wave, which shows the variations of the ever-changing voltage as the coil is rotated for one complete revolution.
Figure 18–10 shows such a sine wave, representing the voltage output generated during one revolution. Note the voltage scale to the left of the curve showing both positive and negative values. The sine wave shows how these values change with respect to the angle of rotation through which the coil has traveled. (One circle of rotation 5 360 degrees.)
In tracing this curve, we find moments when the voltage output is 0. This happens every 180 degrees, when the cutting edge of the coil moves parallel to the lines of flux, Figure 18–9. By contrast, when the cutting edges move perpendicular to the flux lines
(beneath the poles), the rate of cutting flux lines—and therefore the voltage output—is at its maximum. This is shown at the 90-degree and 270-degree points of the sine wave.
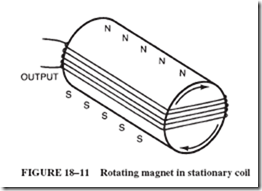
Recall that not all generators are designed to rotate coils within a magnetic field but, instead, rotate a magnet within a stationary coil. The largest generators built contain stationary coils in which useful current is induced by a rotating magnet. Figure 18–11 shows one stationary coil. The cylindrical object shown within the coil represents a rotating magnet that is magnetized along a diameter.
Let us assume that this cylindrical magnet is rotated within the coil and, as the magnetic poles revolve, its flux lines are cut by the stationary conductors of the coil. Such rotation produces an alternating current, just as the repeated motion of the wire in Figure 18–1 produces AC.
To stress an important point once more, we can state that one such revolution produces one cycle of alternating voltage output in the form of a sine wave. Commercial generators in the United States are standardized to produce 60 cycles per second. This standard is known as the frequency of the power supply.
As you progress in your study of electricity, you will learn more about AC. What you need to know at this time is that the induction process in rotating machines produces AC. If direct current (DC) is needed, it can be obtained from AC by using rectifiers.
DC generators achieve rectification by using a commutator instead of slip rings. This is one of the facts to be presented in the next chapter.
SUMMARY
• The voltage produced by generators is called induced emf. This emf is produced either by the motion of wires across a magnetic field or by the motion of a magnetic field across wires.
• This induction process in a generator converts mechanical energy into electrical
energy.
• The amount of induced emf depends on the strength of the magnetic field, the number of turns of wire in the device, and the speed of motion.
• To produce 1 volt, the wire must cut 100,000,000 lines of flux per second.
• Lenz’s law: An induced voltage or current opposes the motion that causes it. An in- duced voltage or current opposes a change of magnetic field.
• Alternating current is generated in stationary coils when a magnet is rotated inside the coil.
• Alternating current is generated in a coil when the coil is rotated in a stationary magnetic field. By means of a commutator, this current is fed into the outside circuit as direct (one-way) current.
Achievement Review
1. A wire is moved through a field, as in the sketch below. What is the direction of the induced emf?
2. In a generator, from where does the electrical energy come?
3. The electric automobile of 1912 was powered only by storage batteries and an electric motor. The necessity of frequent battery charging helped make these cars obsolete. Could a generator, belt-driven from the wheels of a trailer, charge the batteries to make longer trips possible?
4. State three factors on which the amount of induced voltage depends.
5. In a certain generator, like that shown in Figure 18–11, the loop of wire en- closes 10,000 lines of force. What is the total number of lines of force cut during one complete rotation of the magnet?
6. If the magnet of the generator in Figure 18–11 is rotated at a speed of 2,400 rpm, how many lines of force are cut each second? How much voltage is produced?
7. In the generator in the sketch below, determine which brush is positive and which is negative.
8. State Lenz’s law. State the left-hand generator rule. Which one of these is the more important fundamental principle?
9. Figure 18–5 shows a magnet being pulled out from a coil to the right. If the magnet is pulled out to the left, is the induced current in the same direction as shown? Explain your answer.
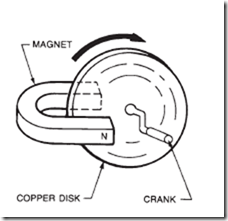
10. A copper disk is supported between magnet poles so it can be rotated, as shown in the sketch. What happens in the disk as it rotates?
11. Does the strength of the magnet in the previous sketch have any effect on the amount of force needed to turn the disk?
12. A coin spinning on the end of a thread is lowered into a magnetic field. Explain what happens and why it does happen.
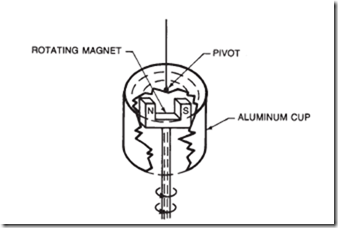
13. An aluminum cup is hung upside down on a pivot over a rotating magnet, as shown in the sketch below. Explain what happens to the cup.