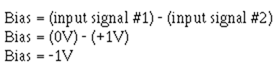Special amplifiers:learning objectives ,input signals in phase ,single-input, single-output, differential amplifier , operational amplifiers and operational amplifier

SPECIAL AMPLIFIERS
LEARNING OBJECTIVES

• Upon completion of this chapter, you will be able to:
• Describe the basic operation of a differential amplifier.
• Describe the operation of a differential amplifier under the following conditions:
• Single Input, Single Output
• Single input, differential output
• Differential input, differential output
• List the characteristics of an operational amplifier.
• Identify the symbol for an operational amplifier.
• Label the blocks on a block diagram of an operational amplifier.
• Describe the operation of an operational amplifier with inverting and noninverting configurations.
• Describe the bandwidth of a typical operational amplifier and methods to modify the bandwidth.
• Identify the following applications of operational amplifiers:
• Adder
• Subtractor
• State the common usage for a magnetic amplifier.
• Describe the basic operation of a magnetic amplifier.
• Describe various methods of changing inductance.
• Identify the purpose of components in a simple magnetic amplifier.

INTRODUCTION

If you were to make a quick review of the subjects discussed in this module up to this point, you would see that you have been given a considerable amount of information about amplifiers. You have been shown what amplification is and how the different classes of amplifiers affect amplification. You also have been shown that many factors must be considered when working with amplifiers, such as impedance, feedback, Frequency response, and coupling. With all this information behind you, you might ask yourself "what more can there be to know about amplifiers?"
There is a great deal more to learn about amplifiers. Even after you finish this chapter you will have only "scratched the surface" of the study of amplifiers. But, you will have prepared yourself for the remainder of the NEETS. This, in turn, should prepare you for further study and, perhaps, a career in electronics.
As in chapter 2, the circuits shown in this chapter are intended to present particular concepts to you. Therefore, the circuits may be incomplete or not practical for use in an actual piece of electronic equipment. You should keep in mind the fact that this text is intended to teach certain facts about amplifiers, and in order to simplify the illustrations used, complete operational circuits are not always shown.
In this chapter three types of special amplifiers are discussed. These are: DIFFERENTIAL AMPLIFIERS, OPERATIONAL AMPLIFIERS, and MAGNETIC AMPLIFIERS. These are called special amplifiers because they are used only in certain types of equipment.
The names of each of these special amplifiers describe the operation of the amplifier, NOT what is amplified. For example, a magnetic amplifier does not amplify magnetism but uses magnetic effects to produce amplification of an electronic signal.
A differential amplifier is an amplifier that can have two input signals and/or two output signals. This amplifier can amplify the difference between two input signals. A differential amplifier will also "cancel out" common signals at the two inputs.
One of the more interesting aspects of an operational amplifier is that it can be used to perform mathematical operations electronically. Properly connected, an operational amplifier can add, subtract, multiply, divide, and even perform the calculus operations of integration and differentiation. These amplifiers were originally used in a type of computer known as the "analog computer" but are now used in many electronic applications.
The magnetic amplifier uses a device called a "saturable core reactor" to control an a.c.output signal. The primary use of magnetic amplifiers is in power control systems.
These brief descriptions of the three special amplifiers are intended to provide you with a general idea of what these amplifiers are and how they can be used. The remaining sections of this chapter will provide you with more detailed information on these special amplifiers.
DIFFERENTIAL AMPLIFIERS
A differential amplifier has two possible inputs and two possible outputs. This arrangement means that the differential amplifier can be used in a variety of ways. Before examining the three basic configurations that are possible with a differential amplifier, you need to be familiar with the basic circuitry of a differential amplifier.
BASIC DIFFERENTIAL AMPLIFIER CIRCUIT
Before you are shown the operation of a differential amplifier, you will be shown how a simpler circuit works. This simpler circuit, known as the DIFFERENCE AMPLIFIER, has one thing in common with the differential amplifier: It operates on the difference between two inputs. However, the difference amplifier has only one output while the differential amplifier can have two outputs.
Format By now, you should be familiar with some amplifier circuits, which should give you an idea of what a difference amplifier is like. In NEETS, module 7, you were shown the basic configurations for transistor amplifiers. Figure 3-1 shows two of these configurations: the common emitter and the common base. In view (A) of figure 3-1 a common-emitter amplifier is shown. The output signal is an amplified version of the input signal and is 180 degrees out of phase with the input signal. View (B) is a common-base amplifier. In this circuit the output signal is an amplified version of the input signal and is in phase with the input signal. In both of these circuits, the output signal is controlled by the base-to-emitter bias. As this bias changes (because of the input signal) the current through the transistor changes. This causes the output signal developed across the collector load (R2) to change. None of this information is new, it is just a review of what you have already been shown regarding transistor amplifiers.
Figure 3-1A. – Common-emitter and common-base amplifiers.

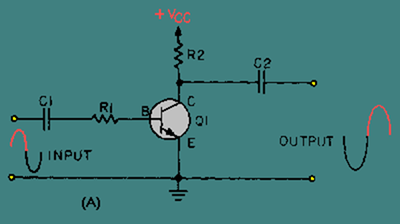
Figure 3-1B. – Common-emitter and common-base amplifiers.

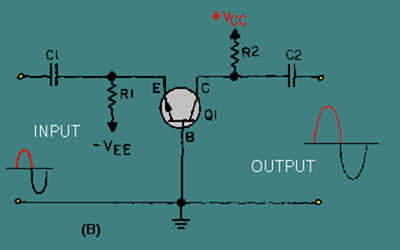
NOTE: Bias arrangements for the following explanations will be termed base-to- emitter. In other publications you will see the term emitter-to-base used to describe the same bias arrangement.
THE TWO-INPUT, SINGLE-OUTPUT, DIFFERENCE AMPLIFIER
If you combine the common-base and common-emitter configurations into a single transistor amplifier, you will have a circuit like the one shown in figure 3-2. This circuit is the two-input, single-output, difference amplifier.
Figure 3-2. – Two-input, single-output, difference amplifier.

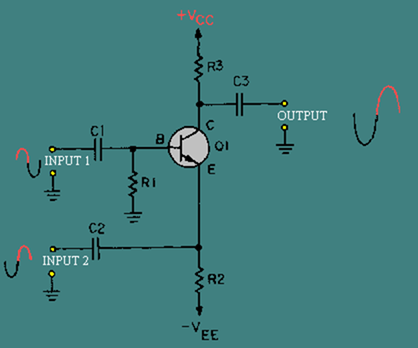
In figure 3-2, the transistor has two inputs (the emitter and the base) and one output (the collector). Remember, the current through the transistor (and therefore the output signal) is controlled by the base-to-emitter bias. In the circuit shown in figure 3-2, the combination of the two input signals controls the output signal. In fact, the DIFFERENCE BETWEEN THE INPUT SIGNALS determines the base-to-emitter bias.
For the purpose of examining the operation of the circuit shown in figure 3-2, assume that the circuit has a gain of -10. This means that for each 1-volt change in the base-to-emitter bias, there would be a 10-volt change in the output signal. Assume, also, that the input signals will peak at 1-volt levels (+1 volt for the positive peak and -1 volt for the negative peak). The secret to understanding this circuit (or any transistor amplifier circuit) is to realize that the collector current is controlled by the base-to-emitter bias. In other words, in this circuit the output signal (the voltage developed across R3) is determined by the difference between the voltage on the base and the voltage on the emitter.

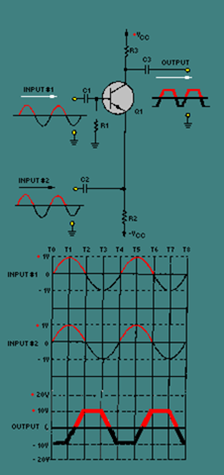
Figure 3-3 shows this two-input, single-output amplifier with input signals that are equal in amplitude and 180 degrees out of phase. Input number one has a positive alternation when input number two has a negative alternation and vice versa.
Figure 3-3. – Input signals 180° out of phase.

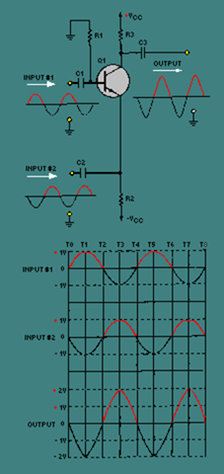
The circuit and the input and output signals are shown at the top of the figure. The lower portion of the figure is a comparison of the input signals and the output signal. Notice the vertical lines marked "T0" through "T8." These represent "time zero" through "time eight." In other words, these lines provide a way to examine the two input signals and the output signal at various instants of time.
In figure 3-3 at time zero (T0) both input signals are at 0 volts. The output signal is also at 0 volts. Between time zero (T0) and time one (T1), input signal number one goes positive and input signal number two goes negative. Each of these voltage changes causes an increase in the base-to-emitter bias which causes current through Q1 to increase. Increased current through Q1 results in a greater voltage drop across the collector load (R3) which causes the output signal to go negative.
By time one (T1), input signal number one has reached +1 volt and input signal number two has reached -1 volt. This is an overall increase in base-to-emitter bias of 2 volts. Since the gain of the circuit is -10, the output signal has decreased by 20 volts. As you can see, the output signal has been determined by the difference between the two input signals. In fact, the base-to-emitter bias can be found by subtracting the value of input signal number two from the value of input signal number one.
Between time one (T1) and time two (T2), input signal number one goes from +1 volt to 0 volts and input signal number two goes from -1 volt to 0 volts. At time two (T2) both input signals are at 0 volts and the base-to-emitter bias has returned to 0 volts. The output signal is also 0 volts.
Between time two (T2) and time three (T3), input signal number one goes negative and input signal number two goes positive. At time three (T3), the value of the base-to-emitter bias is -2 volts.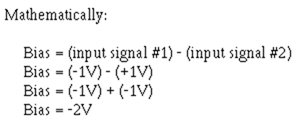
This causes the output signal to be +20 volts at time three (T3).
Between time three (T3) and time four (T4), input signal #1 goes from -1 volt to 0 volts and input signal #2 goes from +1 volt to 0 volts. At time four (T4) both input signals are 0 volts, the bias is 0 volts, and the output is 0 volts.
During time four (T4) through time eight (T8), the circuit repeats the sequence of events that took place from time zero (T0) through time four (T4).
You can see that when the input signals are equal in amplitude and 180 degrees out of phase, the output signal is twice as large (40 volts peak to peak) as it would be from either input signal alone (if the other input signal were held at 0 volts).

Back
Home
Up
Next

Input signals in phase

Figure 3-4 shows the two-input, single-output, difference amplifier with two input signals that are equal in amplitude and in phase.
Figure 3-4. – Input signals in phase.

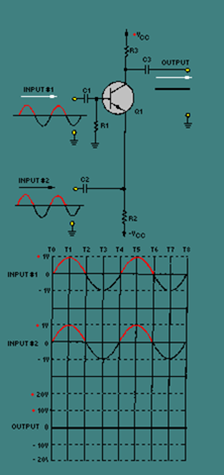
Notice, that the output signal remains at 0 volts for the entire time (T0 – T8). Since the two input signals are equal in amplitude and in phase, the difference between them (the base-to-emitter bias) is always 0 volts. This causes a 0-volt output signal.
If you compute the bias at any time period (T0 – T8), you will see that the output of the circuit remains at a constant zero.

For example:

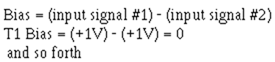
From the above example, you can see that when the input signals are equal in amplitude and in phase, there is no output from the difference amplifier because there is no difference between the two inputs. You also know that when the input signals are equal in amplitude but 180 degrees out of phase, the output looks just like the input except for amplitude and a 180-degree phase reversal with respect to input signal number one. What happens if the input signals are equal in amplitude but different in phase by something other than 180 degrees? This would mean that sometimes one signal would be going negative while the other would be going positive; sometimes both signals would be going positive; and sometimes both signals would be going negative. Would the output signal still look like the input signals? The answer is "no," because figure 3-5 shows a difference amplifier with two input signals that are equal in amplitude but 90 degrees out of phase. From the figure you can see that at time zero (T0) input number one is at 0 volts and input number two is at -1 volt. The base-to-emitter bias is found to be +1 volt.
Figure 3-5. – Input signals 90° out of phase.

This +1-volt bias signal causes the output signal to be -10 volts at time zero (T0). Between time zero (T0) and time one (T1), both input signals go positive. The difference between the input signals stays constant. The effect of this is to keep the bias at +1 volt for the entire time between T0 and T1. This, in turn, keeps the output signal at -10 volts.
Between time one (T1) and time two (T2), input signal number one goes in a negative direction but input signal number two continues to go positive. Now the difference between the input signals decreases rapidly from +1 volt. Halfway between T1 and T2 (the dotted vertical line), input signal number one and input signal number two are equal in amplitude. The difference between the input signals is 0 volts and this causes the output signal to be 0 volts. From this point to T2 the difference between the input signals is a negative value. At T2:

From time two (T2) to time three (T3), input signal number one goes negative and input signal number two goes to zero. The difference between them stays constant at -1 volt. Therefore, the output signal stays at a +10-volt level for the entire time period from T2 to T3. At T3 the bias condition will be:
Between T3 and T4 input signal number one goes to zero while input signal number two goes negative. This, again, causes a rapid change in the difference between the input signals. Halfway between T3 and T4 (the dotted vertical line) the two input signals are equal in amplitude; therefore, the difference between the input signals is 0 volts, and the output signal becomes 0 volts. From that point to T4, the difference between the input signals becomes a positive voltage. At T4:

(The sequence of events from T4 to T8 are the same as those of T0 to T4.)
As you have seen, this amplifier amplifies the difference between two input signals. But this is NOT a differential amplifier. A differential amplifier has two inputs and two outputs. The circuit you have just been shown has only one output. Well then, how does a differential amplifier schematic look?
TYPICAL DIFFERENTIAL AMPLIFIER CIRCUIT
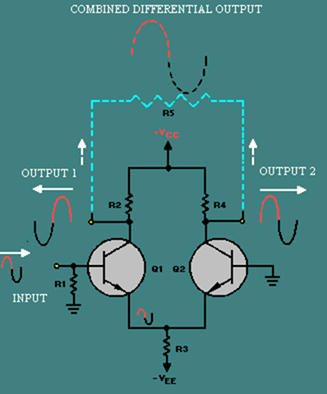
Figure 3-6 is the schematic diagram of a typical differential amplifier. Notice that there are two inputs and two outputs. This circuit requires two transistors to provide the two inputs and two outputs. If you look at one input and the transistor with which it is associated, you will see that each transistor is a common-emitter amplifier for that input (input one and Q1; input two and Q2). R1 develops the signal at input one for Q1, and R5 develops the signal at input two for Q2. R3 is the emitter resistor for both Q1 and Q2. Notice that R3 is NOT bypassed. This means that when a signal at input one affects the current through Q1, that signal is developed by R3. (The current through Q1 must flow through R3; as this current changes, the voltage developed across R3 changes.) When a signal is developed by R3, it is applied to the emitter of Q2. In the same way, signals at input two affect the current of Q2, are developed by R3, and are felt on the emitter of Q1. R2 develops the signal for output one, and R4 develops the signal for output two.
Figure 3-6. – Differential amplifier.

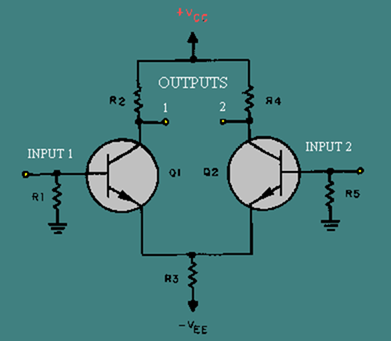
Even though this circuit is designed to have two inputs and two outputs, it is not necessary to use both inputs and both outputs. (Remember, a differential amplifier was defined as having two possible inputs and two possible outputs.) A differential amplifier can be connected as a single-input, single-output device; a single-input, differential-output device; or a differential-input, differential-output device.

Q.1 How many inputs and outputs are possible with a differential amplifier?

Q.2 What two transistor amplifier configurations are combined in the single-transistor, two-input, single-output difference amplifier?

Q.3 If the two input signals of a difference amplifier are in phase and equal in amplitude, what will the output signal be?

Q.4 If the two input signals to a difference amplifier are equal in amplitude and 180 degrees out of phase, what will the output signal be?

Q.5 If only one input signal is used with a difference amplifier, what will the output signal be?

Q.6 If the two input signals to a difference amplifier are equal in amplitude but neither in phase nor 180 degrees out of phase, what will the output signal be?

Back
Home
Up
Next

SINGLE-INPUT, SINGLE-OUTPUT, DIFFERENTIAL AMPLIFIER

Figure 3-7 shows a differential amplifier with one input (the base of Q1) and one output (the collector of Q2). The second input (the base of Q2) is grounded and the second output (the collector of Q1) is not used.
Figure 3-7. – Single-input, single-output differential amplifier.

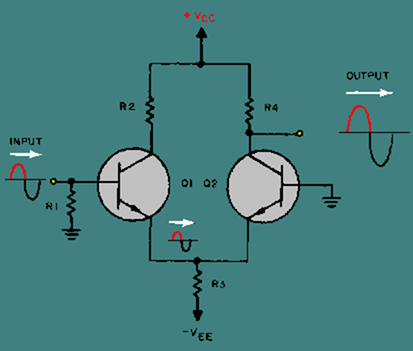
When the input signal developed by R1 goes positive, the current through Q1 increases. This increased current causes a positive-going signal at the top of R3. This signal is felt on the emitter of Q2. Since the base of Q2 is grounded, the current through Q2 decreases with a positive-going signal on the emitter. This decreased current causes less voltage drop across R4. Therefore, the voltage at the bottom of R4 increases and a positive-going signal is felt at the output.
When the input signal developed by R1 goes negative, the current through Q1 decreases. This decreased current causes a negative-going signal at the top of R3. This signal is felt on the emitter of Q2. When the emitter of Q2 goes negative, the current through Q2 increases. This increased current causes more of a voltage drop across R4. Therefore, the voltage at the bottom of R4 decreases and a negative-going signal is felt at the output.
This single-input, single-output, differential amplifier is very similar to a single-transistor amplifier as far as input and output signals are concerned. This use of a differential amplifier does provide amplification of a.c. or d.c. signals but does not take full advantage of the characteristics of a differential amplifier.
SINGLE-INPUT, DIFFERENTIAL-OUTPUT, DIFFERENTIAL AMPLIFIER
In chapter one of this module you were shown several phase splitters. You should remember that a phase splitter provides two outputs from a single input. These two outputs are 180 degrees out of phase with each other. The single-input, differential-output, differential amplifier will do the same thing.
Figure 3-8 shows a differential amplifier with one input (the base of Q1) and two outputs (the collectors of Q1 and Q2). One output is in phase with the input signal, and the other output is 180 degrees out of phase with the input signal. The outputs are differential outputs.
Figure 3-8. – Single-input, differential-output differential amplifier.

This circuit’s operation is the same as for the single-input, single-output differential

amplifier just described. However, another output is obtained from the bottom of R2. As the input signal goes positive, thus causing increased current through Q1, R2 has a greater voltage drop. The output signal at the bottom of R2 therefore is negative going. A negative-going input signal will decrease current and reverse the polarities of both output signals.
Now you see how a differential amplifier can produce two amplified, differential output signals from a single-input signal. One further point of interest about this configuration is that if a combined output signal is taken between outputs number one and two, this single output will be twice the amplitude of the individual outputs. In other words, you can double the gain of the differential amplifier (single output) by taking the output signal between the two output terminals. This single-output signal will be in phase with the input signal. This is shown by the phantom signal above R5 (the phantom resistor connected between outputs number one and two would be used to develop this signal).
DIFFERENTIAL-INPUT, DIFFERENTIAL-OUTPUT, DIFFERENTIAL AMPLIFIER
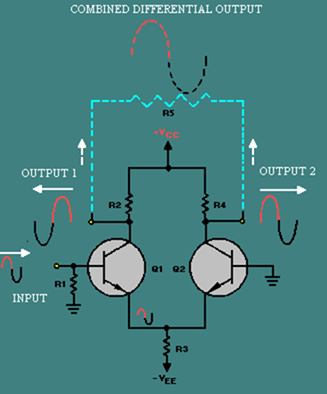
When a differential amplifier is connected with a differential input and a differential output, the full potential of the circuit is used. Figure 3-9 shows a differential amplifier with this type of configuration (differential-input, differential-output).
Figure 3-9. – Differential-input, differential-output differential amplifier.]

Normally, this configuration uses two input signals that are 180 degrees out of phase. This causes the difference (differential) signal to be twice as large as either input alone. (This is just like the two-input, single-output difference amplifier with input signals that are 180 degrees out of phase.)
Output number one is a signal that is in phase with input number two, and output number two is a signal that is in phase with input number one. The amplitude of each output signal is the input signal multiplied by the gain of the amplifier. With 180-degree-out-of-phase input signals, each output signal is greater in amplitude than either input signal by a factor of the gain of the amplifier.
When an output signal is taken between the two output terminals of the amplifier (as shown by the phantom connections, resistor, and signal), the combined output signal is twice as great in amplitude as either signal at output number one or output number two. (This is because output number one and output number two are 180 degrees out of phase with each other.) When the input signals are 180 degrees out of phase, the amplitude of the combined output signal is equal to the amplitude of one input signal multiplied by two times the gain of the amplifier.
When the input signals are not 180 degrees out of phase, the combined output signal taken across output one and output two is similar to the output that you were shown for the two-input, single-output, difference amplifier. The differential amplifier can have two outputs (180 degrees out of phase with each other), or the outputs can be combined as shown in figure 3-9.
In answering Q7 through Q9 use the following information: All input signals are sine waves with a peak-to-peak amplitude of 10 millivolts. The gain of the differential amplifier is 10.

Q.7 If the differential amplifier is configured with a single input and a single output, what will the peak-to-peak amplitude of the output signal be?

Q.8 If the differential amplifier is configured with a single input and differential outputs, what will the output signals be?

Q.9 If the single-input, differential-output, differential amplifier has an output signal taken between the two output terminals, what will the peak-to-peak amplitude of this combined output be?
In answering Q10 through Q14 use the following information: A differential amplifier is configured with a differential input and a differential output. All input signals are sine waves with a peak-to-peak amplitude of 10 millivolts. The gain of the differential amplifier is 10.
Q.10 If the input signals are in phase, what will be the peak-to-peak amplitude of the output signals?

Q.11 If the input signals are 180 degrees out of phase with each other, what will be the peak-to-peak amplitude of the output signals?

Q.12 If the input signals are 180 degrees out of phase with each other, what will the
phase relationship be between (a) the output signals and (b) the input and output signals?

Q.13 If the input signals are 180 degrees out of phase with each other and a combined output is taken between the two output terminals, what will the amplitude of the combined output signal be?

Q.14 If the input signals are 90 degrees out of phase with each other and a combined output is taken between the two output terminals, (a) what will the peak-to-peak amplitude of the combined output signal be, and (b) will the combined output signal be a sine wave?

Back
Home
Up
Next

OPERATIONAL AMPLIFIERS

An OPERATIONAL AMPLIFIER (OP AMP) is an amplifier which is designed to be used with other circuit components to perform either computing functions (addition, subtraction) or some type of transfer operation, such as filtering. Operational amplifiers are usually high-gain amplifiers with the amount of gain determined by feedback.
Operational amplifiers have been in use for some time. They were originally developed for analog (non-digital) computers and used to perform mathematical functions. Operational amplifiers were not used in other devices very much because they were expensive and more complicated than other circuits.
Today many devices use operational amplifiers. Operational amplifiers are used as d.c. amplifiers, a.c. amplifiers, comparators, oscillators (which are covered in NEETS, module 9), filter circuits, and many other applications. The reason for this widespread use of the operational amplifier is that it is a very versatile and efficient device. As an integrated circuit (chip) the operational amplifier has become an inexpensive and readily available "building block" for many devices. In fact, an operational amplifier in integrated circuit form is no more expensive than a good transistor.
CHARACTERISTICS OF AN OPERATIONAL AMPLIFIER
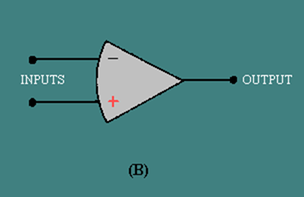
The schematic symbols for an operational amplifier are shown in figure 3-10. View (A) shows the power supply requirements while view (B) shows only the input and output terminals. An operational amplifier is a special type of high-gain, d.c. amplifier. To be classified as an operational amplifier, the circuit must have certain characteristics. The three most important characteristics of an operational amplifier are:

• Very high gain
• Very high input impedance
• Very low output impedance

Figure 3-10A. – Schematic symbols of an operational amplifier.

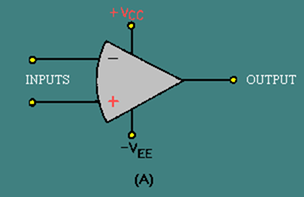Figure 3-10B. – Schematic symbols of an operational amplifier.

Since no single amplifier stage can provide all these characteristics well enough to be considered an operational amplifier, various amplifier stages are connected together. The total circuit made up of these individual stages is called an operational amplifier. This circuit (the operational amplifier) can be made up of individual components (transistors, resistors, capacitors, etc.), but the most common form of the operational amplifier is an integrated circuit. The integrated circuit (chip) will contain the various stages of the operational amplifier and can be treated and used as if it were a single stage.
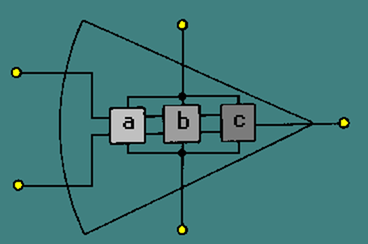
BLOCK DIAGRAM OF AN OPERATIONAL AMPLIFIER
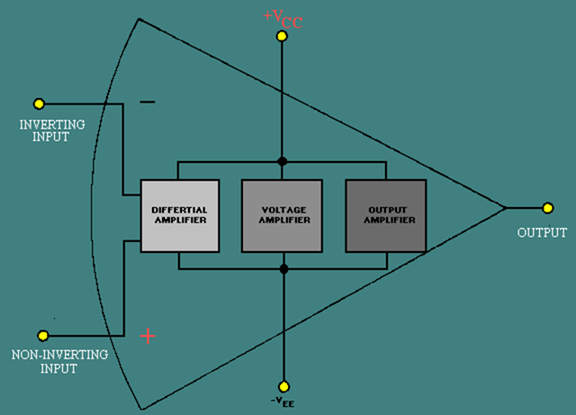
Figure 3-11 is a block diagram of an operational amplifier. Notice that there are three stages within the operational amplifier.
Figure 3-11. – Block diagram of an operational amplifier.

The input stage is a differential amplifier. The differential amplifier used as an input stage provides differential inputs and a Frequency response down to d.c. Special techniques are used to provide the high input impedance necessary for the operational amplifier.
The second stage is a high-gain voltage amplifier. This stage may be made from several transistors to provide high gain. A typical operational amplifier could have a voltage gain of 200,000. Most of this gain comes from the voltage amplifier stage.
The final stage of the OP AMP is an output amplifier. The output amplifier provides low output impedance. The actual circuit used could be an emitter follower. The output stage should allow the operational amplifier to deliver several milliamperes to a load.
Notice that the operational amplifier has a positive power supply (+V CC) and a negative power supply (-VEE). This arrangement enables the operational amplifier to produce either a positive or a negative output.
The two input terminals are labeled "inverting input" (-) and "noninverting input" (+). The operational amplifier can be used with three different input conditions (modes). With differential inputs (first mode), both input terminals are used and two input signals which are 180 degrees out of phase with each other are used. This produces an output signal that is in phase with the signal on the noninverting input. If the noninverting input is grounded and a signal is applied to the inverting input (second mode), the output signal will be 180 degrees out of phase with the input signal (and one-half the amplitude of the first mode output). If the inverting input is grounded and a signal is applied to the noninverting input (third mode), the
output signal will be in phase with the input signal (and one-half the amplitude of the first mode output).

Q.15 What are the three requirements for an operational amplifier?

Q.16 What is the most commonly used form of the operational amplifier?

Q.17 Draw the schematic symbol for an operational amplifier.

Q.18 Label the parts of the operational amplifier shown in figure 3-12.

Back
Home
Up
Next

Operational amplifier

Figure 3-12. – Operational amplifier.

CLOSED-LOOP OPERATION OF AN OPERATIONAL AMPLIFIER
Operational amplifiers can have either a closed-loop operation or an open-loop operation. The operation (closed-loop or open-loop) is determined by whether or not feedback is used. Without feedback the operational amplifier has an open-loop operation. This open-loop operation is practical only when the operational amplifier is used as a comparator (a circuit which compares two input signals or compares an input signal to some fixed level of voltage). As an amplifier, the open-loop operation is not practical because the very high gain of the operational amplifier creates poor stability. (Noise and other unwanted signals are amplified so much in open-loop operation that the operational amplifier is usually not used in this way.) Therefore, most operational amplifiers are used with feedback (closed-loop operation).
Operational amplifiers are used with degenerative (or negative) feedback which reduces the gain of the operational amplifier but greatly increases the stability of the circuit. In the closed-loop configuration, the output signal is applied back to one of the input terminals. This feedback is always degenerative (negative). In other words, the feedback signal always opposes the effects of the original input signal. One result of degenerative feedback is that the inverting and noninverting inputs to the operational amplifier will be kept at the same potential.
Closed-loop circuits can be of the inverting configuration or noninverting configuration. Since the inverting configuration is used more often than the noninverting configuration, the inverting configuration will be shown first.
Inverting Configuration
Figure 3-13 shows an operational amplifier in a closed-loop, inverting configuration. Resistor R2 is used to feed part of the output signal back to the input of the operational amplifier.
Figure 3-13. – Inverting configuration.

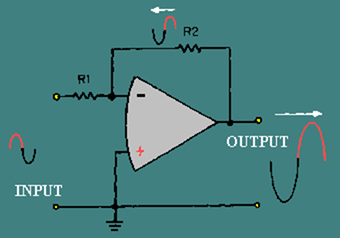
At this point it is important to keep in mind the difference between the entire circuit (or operational circuit) and the operational amplifier. The operational amplifier is represented by the triangle-like symbol while the operational circuit includes the resistors and any other components as well as the operational amplifier. In other words, the input to the circuit is shown in figure 3-13, but the signal at the inverting input of the operational amplifier is determined by the feedback signal as well as by the circuit input signal.
As you can see in figure 3-13, the output signal is 180 degrees out of phase with the input signal. The feedback signal is a portion of the output signal and, therefore, also 180 degrees out of phase with the input signal. Whenever the input signal goes positive, the output signal and the feedback signal go negative. The result of this is that the inverting input to the operational amplifier is always very close to 0 volts with this configuration. In fact, with the noninverting input grounded, the voltage at the inverting input to the operational amplifier is so small compared to other voltages in the circuit that it is considered to be VIRTUAL GROUND. (Remember, in a closed-loop operation the inverting and noninverting inputs are at the same potential.)
Virtual ground is a point in a circuit which is at ground potential (0 volts) but is NOT connected to ground. Figure 3-14, (view A) (view B) and (view C), shows an example of several circuits with points at virtual ground.
Figure 3-14A. – Virtual ground circuits.

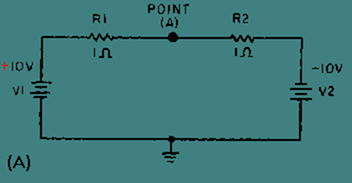
Figure 3-14B. – Virtual ground circuits.

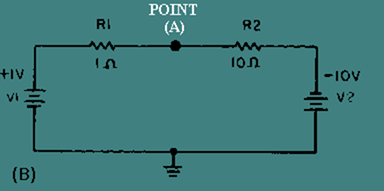
Figure 3-14C. – Virtual ground circuits.

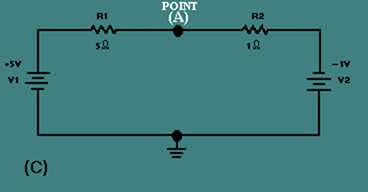
In view (A), V1 (the left-hand battery) supplies +10 volts to the circuit while V2 (the right-hand battery) supplies -10 volts to the circuit. The total difference in potential in the circuit is 20 volts.
The total resistance of the circuit can be calculated: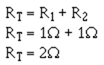
Now that the total resistance is known, the circuit current can be calculated: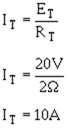
The voltage drop across R1 can be computed: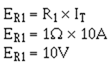
The voltage at point A would be equal to the voltage of V1 minus the voltage drop of R1.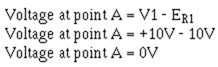
To check this result, compute the voltage drop across R2 and subtract this from the voltage at point A. The result should be the voltage of V2.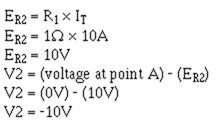
It is not necessary that the voltage supplies be equal to create a point of virtual ground. In view (B) V1 supplies +1 volt to the circuit while V2 supplies -10 volts. The total difference in potential is 11 volts. The total resistance of this circuit (R1 + R2) is 11 ohms. The total current (IT) is 1 ampere. The voltage drop across R1 (E R1 = R1 X IT) is 1 volt. The voltage drop across R2 (ER2 = R2 X I T) is 10 volts. The voltage at
point A can be computed: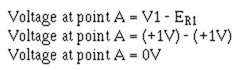
So point A is at virtual ground in this circuit also. To check the results, compute the voltage at V2.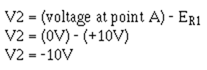

Back
Home
Up
Next