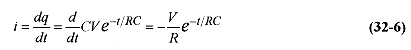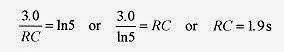R-C Circuits
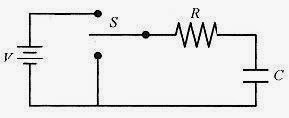
Our first look at R-C circuits is with a simple word description of the charging phenomenon. The circuit shown in Fig. 32-1 is appropriate for the study of charging and discharging. After giving a general description of how the circuit works, we will take a closer look at the mathematical description. Throughout the discussion, unless the context and notation indicate otherwise, lower case letters mean time varying quantities and upper case letters constants. For example, q is the symbol for time varying charge on the capacitor while Q is the total charge.
Fig. 32-1
Charging.
Assume the capacitor has zero charge and voltage, and place the switch (S) in the charging position (up). When the battery voltage is applied to the R and C in series, current begins to flow. Current through the resistor causes a voltage drop across the resistor. Because of this voltage drop, less than the battery voltage is applied to the capacitor. As current flows, the capacitor charges and less and less current flows until there is no current, no voltage across the resistor and the capacitor is charged to the battery voltage (Q=CV).
The charge on the capacitor increases with time starting with zero charge and eventually reaching maximum charge of CV following an exponential function.
This function fits our understanding of how the circuit operates since when t = 0, q is zero, and when t is very large, q=CV, the capacitor is totally charged.
The voltage on the capacitor is 
Here the notation VC denotes the time varying voltage on the capacitor.
The current in the circuit declines exponentially according to i=(V/R)e-t/RC
With this description of the operation of the charging circuit, we can proceed to a more detailed (mathematical) analysis of the charging situation.
When the battery voltage is applied to R and C, voltages across these components vary with time. We can, however, write a Kirchhoff-type voltage statement that is correct for the entire time the circuit is charging. This is called an instantaneous voltage statement; it is true at any instant of time. Following Kirchhoff’s law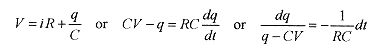 
This equation can be integrated with a change of variable. Replace q-CV with x so dq = dx.
Then 
The integral of the left side is In(x)=In(q-CV), so
Choosing the constant as InK1 is very convenient, allowing further simplification.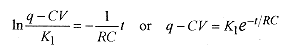
Notice that the logarithm equation goes into an exponential equation. This is not an every day mathematical operation. Review the Introduction, Mathematical Background, and be sure you understand how to go from a logarithmic equation to an exponential one. Rewrite the equation 
and apply the condition that at t=0, q=0, or 0 = CV + K1, or K1 = –CV, so finally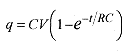 
Obtaining this expression for q looks easy, and it is if you remember to choose the constant for convenience in solving the equation, remember how to switch from a logarithmic equation to an exponential equation, and apply the initial conditions correctly.
The voltage across the capacitor is 
The current in the resistor is
The voltage across the resistor is 
Two graphs are particularly helpful in understanding the situation; one of q versus t,and the other of i versus t.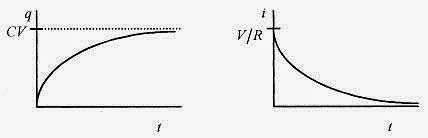 
Fig. 32-2
Notice in the curve of q versus t, that at t = 0, q = 0, and as t → ∞, q → CV.
In the curve of i versus t, at t=0, i=V/R, and as t → ∞, i → 0.
At t = 0, the charge on the capacitor is zero and the current is maximum; and as t goes to infinity, the current goes to zero and the charge reaches its maximum of CV.
The Time Constant
In biological systems that grow exponentially the systems are often characterized by giving the doubling time, the time for the system to double in number, size, or mass. In electrical systems that grow exponentially the systems are characterized by a time constant, the time to make the exponent of e equal to 1. The time constant for this circuit is RC (see equation 32-1). As an exercise verify that the units of RC are seconds.
Look at equation 32-1 and the q versus t graph. When t=RC, 1-e-1=0.63 and the charge on the capacitor has risen to 0.63 of its final value. A similar statement can be made about the voltage on the capacitor. After one time constant, the voltage on the capacitor is 0.63 of the battery voltage.
The current, meanwhile, has in one time constant dropped to e-1 = 0.37 of its initial value.
32-1 A 10kΩ resistor and a 20μF capacitor are placed in series with a 12V battery. Find the charge on the capacitor, the current, and the voltages on the capacitor and resistor at the instant the switch is closed, t = 0.
Solution: At t = 0 the charge on the capacitor is zero.
At t=0, the current is i=V/R=12V/10×103Ω=1.2×10-3A.
At t=0, the voltage on the capacitor is zero (it has no charge) and the entire battery voltage of 12V is across the resistor.
<><><><><><><><><><><><>
32-2 For the circuit of problem 32-1, find the time constant, and the charge, current, and VR, and VC at a time equal to one time constant.
Solution: The time constant is RC=10×103Ω.20×10-6F = 0.20s.
The charge on the capacitor at t = 0.20s is
The current at t= 0.20s is 
The voltage across the capacitor is VC=V(1-e-1)=12V.0.63=7.6V.
The voltage across the resistor is 12V-7.6V=4.4 V.
These problems can be deceptively easy. Be sure you know how to manipulate the exponents on your calculator. Don’t get a test problem wrong because you did not practice all the steps in the problem and were unfamiliar with manipulating exponents on your calculator.
<><><><><><><><><><><><>
32-3 For the circuit of problem 32-1, how long does it take for the capacitor to reach 80% of its final charge?
Solution: This problem is similar to radioactive decay problems where we want to know the time for half the material to decay. There is a fair amount of algebraic manipulation that is easier to follow without numbers, so the problem will be worked as far as possible with symbols.
Start with q=CV(1-e-t/RC) and note that the final (fully charged) q is equal to CV.
Mathematically, when t → ∞, e-t/RC → 1 so q → CV.
To find the time for 80% charge set q equal to 80% of the final charge, or q=0.80CV, and solve for t.
For convenience switch to positive exponents so 1/e-t/RC=0.20 or e-t/RC=1/0.20=5
In order to solve for t, switch the exponential equation to a logarithmic equation. One of the functions of logarithms is to solve for variables in exponents. 
Now put in the values for R and C.
As a check note that 1-e-t/RC=1-e-0.32/0.20=0.80
Discharging
After the capacitor is left to charge for a long time (many time constants) the charge is CV. Move the switch to the discharge position (down in Fig. 32-1) where R and C are in series. When the charged capacitor and resistor are placed in series the charged capacitor acts as a battery. The voltage on the capacitor is q/C, and this voltage appears across the resistor as iR. As time goes on, the charge on the capacitor is depleted and the current drops (eventually) to zero. The charge decays according to 
and the current according to
The negative sign indicates that the current in the resistor is in the opposite direction from the charging situation, which must be the case.
Mathematical analysis of the discharge circuit starts with a Kirchhoffs law loop type of statement.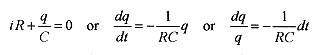 
and solving
Again notice that the choice of constant is very convenient because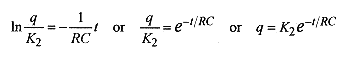
Now impose the initial condition, At t=0, q=CV, so K2=CV and 
The charge on the capacitor decays with the same time constant, RC.
32-4 For the circuit described in problem 32-1 placed in the discharge mode, how long does it take for the circuit to discharge to 50% of its original (total) charge?
Solution: Solve equation 32-5 for t when q=0.50CV 
It is more convenient to write 0.50 as 1/2, so when the statement is converted to logarithms,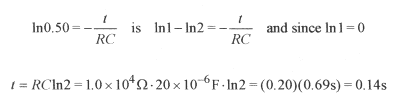
In terms of time constants this would be 1n2 time constants, or 0.69 of a time constant.
It makes sense that our answer is less than one time constant since it takes less time for the charge to decline to 50% of its initial value than to 37% (1/e) of its initial value.
32-5 An RC circuit is observed during discharge to have an initial capacitor potential of 100V and after 3.0s to have a potential of 20V. How long will it take for the capacitor to discharge to 1.0V.
Solution: The voltage across the capacitor at any time is determined by equation 32-5 rewritten as q/C, or VC=Voe-t/RC, where Vo is the voltage at t = 0.
Take Vo=100, VC = 20V, and t = 3.0s and write
Switching to logarithms
Knowing this number, the specific decay law for this circuit can be written V = 100Ve-t/1.9.
Now calculate the time for the voltage to drop to 1.0V.
Switching to logarithms
Go back over this problem and note the procedure.
1. After reading the problem, the general law (equation) was written down, VC=Voe-t/RC
2. Next the data from the problem (100V going to 20V in 3.0s) was used to find RC.
3. With RC the specific law for this problem was written, V=100Ve-t/1.9.
4. Finally, with this specific law the predictive calculation was performed to find the time for the 100V to decay to 1.0V.
This analysis procedure is typical of growth and decay problems in general. Be familiar with the steps in this procedure. It will keep you from getting lost and not knowing how to proceed in problems like this.