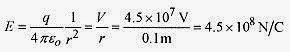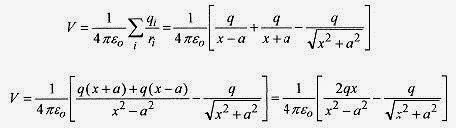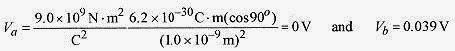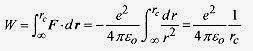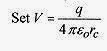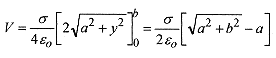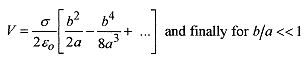Electric Potential
In mechanics the use of force to analyze problems works well when the force is a constant. When the forcedepends on position, then the concepts of work and energy are introduced with work defined as the summation,or integral, of force over distance.
In electricity, potential is introduced for similar reasons. While the electric field is a constant in many problems,it is not a constant, say, in the vicinity of a point charge except on a sphere surrounding that (central) charge.Any motion of charges due to electric force that is not on the surface of the sphere surrounding a central char gehas to take account of this non-constancy of the field, or force (field is force per charge).
The electric potential or potential difference between two points A and B is defined as the work per unit charge necessary to move the unit charge from A to B![]()
The units of potential are Joule/Coulomb or volt. Usually one point (A) is taken at infinity where VA=0. This is convenient and correct since the force on the unit charge at infinity (see Coulomb’s law) is zero.
Look at the integral (same definition of work as in mechanics) involved in calculating WAB for a charge qo being brought from infinity to the vicinity of q. This integral is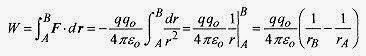
Fig. 27-1
Be careful of the signs here; If q and qo are positive, the force is repulsive; and if qo is coming from infinity torB, then F.dr is negative. With this definition the potential, or work per unit charge, at any point r radially out from q is![]()
a most convenient definition.
For a constant electric field, such as between two parallel plates, WAB=Fd=qoEd and VB-VA=WAB/qo=Ed, where dis the distance moved (in the direction of the field).
27-1 In a certain experiment an electric field of 2.0×105 N/C is required for parallel plates separated by0.0020m. What voltage will produce this field?
Solution: For a constant field, V = Ed so![]()
<><><><><><><><><><><><>
27-2 An electron placed between two charged parallel plates separated by 2.0×10-2m is observed to accelerate at5.0×1014m/s2. What is the voltage on the plates?
Solution: First calculate the force on the electron as![]()
The electric field required to move this electron is![]()
The voltage for this separation is![]()
<><><><><><><><><><><><>
27-3 What is the electric potential 0.20m away from a charge of 1.0 × 10-6C?
Solution:27-4 Calculate the electric potential for the same charge but at 0.50m away.
Solution:The potential difference between these two positions is 2.7 × 104V
<><><><><><><><><><><><>
27-5 Use the situation (charge and potential calculations) of problems 27-3 and 27-4. If a charge of 5.0×10-6Cwere moved from a radius of 0.50m to a radius of 0.20m, how much work would be performed?
Solution: The work performed is the potential difference in Joule/Coulomb (or volt) times the charge in Coulomb (observe the units carefully).![]()
The work is independent of the path between these radii. This is the great value of potential calculations.
<><><><><><><><><><><><>
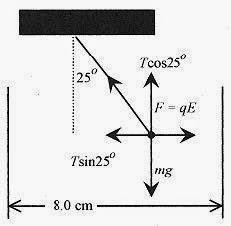
27-6 A 5.0g conducting sphere with charge of 20 μC hangs by a non-conducting thread in an electric field
produced by two plates separated by 8.0cm. What potential will cause the ball to hang at 25° to the vertical?
Fig. 27-2
Solution: This is a force-balance problem, the electric force is balanced by the horizontal component of the tension in the thread. Refer to Fig. 27-2 and write the force statements.
Divide one by the other to arrive at ![]()
The potential is from E = V/d or V = Ed![]()
<><><><><><><><><><><><>
27-7 Calculate the electric potential of a spherical (conducting) shell of radius 0.10m carrying a charge of5.0×10-4C.
Solution: In calculating the potential on the spherical shell the charge acts as if it were at the center of the sphere.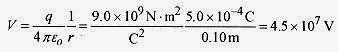
<><><><><><><><><><><><>
27-8 Now calculate the electric field just outside this surface.
As an exercise show that the unit V/m is equal to N/C.
<><><><><><><><><><><><>
The electric potential due to an array of charges can be calculated by superposing the solutions for each charge.Because the electric potential is not a vector this is usually an easy calculation.
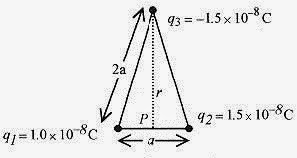
27-9 For the array shown in Fig. 27-3 calculate the potential mid-way between q1 and q2.
Solution: First calculate the distance from this midpoint to q3![]()
The potential at the point P is the sum of the contributions from each of the charges.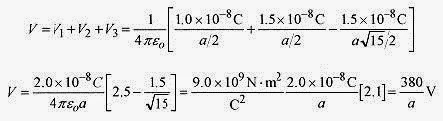
if a is measured in meters.
<><><><><><><><><><><><>
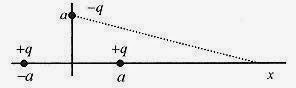
27-10 Calculate the electric potential along the x-axis for the triangular array of charges shown.
Fig. 27-4
Solution:
for
which is 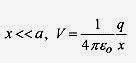 what we would expect.
what we would expect.
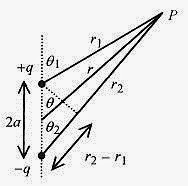
A long way away from the collection of charges the collection looks like one positive charge.A classic problem is the calculation of the potential at a point a distance r and at an angle θ from the center of adipole. The potential is written by summing the potential from the two charges and using the approximatetrigonometric relation between r, r1, and r2.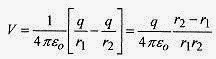
If r>>a then r1r2 ≈ r2 and also θ1 ≈ θ2 ≈ so r2–r1 ≈ 2a cosθ and using the dipole definition p=2aq
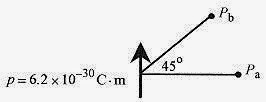
27-11 The water molecule H2O has an asymmetric charge distribution leading to a dipole moment p of 6.2×10-30C.m. Calculate the electric potential 1.0nm a) at right angles to the direction of the dipole moment and b) at45° to the direction of the dipole moment. (1.0 nm is approximately 10 hydrogen atom diameters)
Fig. 27-6
Solution: The approximate expression for the electric potential is 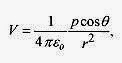
and the electric potentials at Pa and Pb are
ccap
27-12 A positron (positively charged electron) traveling at 3.0×107 m/s is projected directly at a stationaryproton. What is the distance of closest approach?
Solution: The positron will approach the proton until the energy of the positron is expended in doing workagainst the Coulomb repulsive force. The positron will stop, then exit the vicinity of the proton having avelocity profile on exit the same as, but in the opposite direction, to the entrance.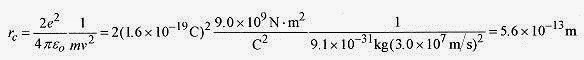
This work is set equal to the kinetic energy 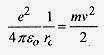 and solved for
and solved for![]() This is a very close approach being two orders of magnitude smaller than the distance from the nucleus to thefirst electron orbit radius in the hydrogen atom.
This is a very close approach being two orders of magnitude smaller than the distance from the nucleus to thefirst electron orbit radius in the hydrogen atom.
Second Solution: This problem can be done using the concept of the electron-volt (eV) unit of energy. Anelectron accelerated through one volt has an amount of work performed on it equal to one volt (the work per unit charge) times the charge on the electron.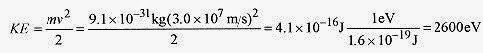 This equation defines the Joule-eV equivalence. An electron accelerated through a potential difference of onevolt is said to gain one electron volt in energy. An electron accelerated through 1000 volts would gain 1000 eVin energy. An alpha particle (two positive electronic charges) accelerated through 1000 volts would gain 2000eV in energy.
This equation defines the Joule-eV equivalence. An electron accelerated through a potential difference of onevolt is said to gain one electron volt in energy. An electron accelerated through 1000 volts would gain 1000 eVin energy. An alpha particle (two positive electronic charges) accelerated through 1000 volts would gain 2000eV in energy.
In this particular problem the positron with a velocity of 3.0 × 107 m/s has a kinetic energy of
This means that the positron has been accelerated through 2600 V.
A positron with this energy could approach a proton to a radius equivalent to 2600 volt potential.
equal to 2600V and solve for r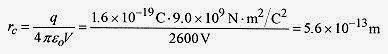
c<><><><><><><><><><><><>
Another application of the concept of potential is to calculate the amount of work required to place charges inan array.
27-13 Calculate the work required to arrange the charges as shown in Fig. 27-7. In this problem the subscriptson the q’s represent the position of the charges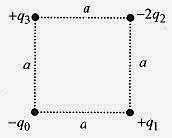
Fig. 27-7
Solution: To make this calculation place q0 in position (corresponding to the origin of a coordinate system) andcalculate the work necessary to place q1 in position. This is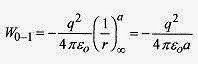
Since the charges are opposite, the electric force is attractive and the work to put this charge in position isnegative (this charge has to be restrained as it approaches q0). Now with these charges in place, add -2q2 with anamount of work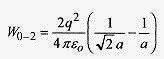
There are two components to this work calculation, the work to bring -2q2 to within of –q0 and the work tobring -2q2 to within a of +q1. Adding the third charge means taking into account the three charges already inplace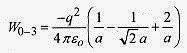
The total work is the sum of these, or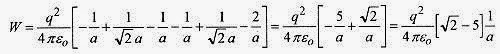
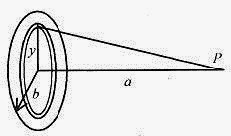
27-14 Another classic problem has to do with the calculation of the electric potential due to charge on a surfacealong a line from the center of a disk and perpendicular to the disk.
Fig. 27-8
In this problem dq will have to be written in terms of charge per unit area times (differential) area. Start bywriting the differential voltage in terms of the differential element of charge, dq, or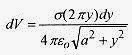
The charge on the surface is assumed uniform with surface charge density σ (charge per unit area). Take thecharge contained in the circular strip, σ(2πy)dy (2 πy is the length of the strip and dy is the width). The r is, ![]()
so the contribution of this strip to the electric potential is
The integration is to be performed in y from zero to b, the radius of the disk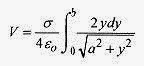
Make a change of variable. Let u = a2 + y2 and du = 2ydy so the integral becomes (and we look at the integralonly without the limits)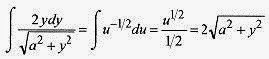
This integral is in the Introduction, Mathematical
Background.
Now look at the limiting case where b/a <<1, which is often the case. This is most conveniently done by firstrewriting the expression in brackets as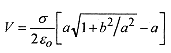
and then writing the square root as a binomial expansion remembering that b/a <<1. The binomial expansion(see the Introduction, Mathematical Background for the binomial expansion) is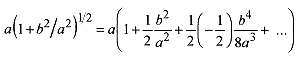
This is expected since σπb2 is the total charge and a is the distance from that charge. A long way away a disk ofcharge “looks like” a point charge. The use of the binomial expansion is helpful in two ways. First, it allows aconvenient calculation for the situation where b/a <<1; and second, the limiting case reduces to the simpleexpression for the potential due to a point charge, in effect verifying the calculation