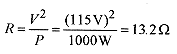Conductivity
Electric conductivity is most conveniently thought of as motion by essentially “free” electrons; electrons not bound to atoms. The actual mechanism is more complicated but this simple view is sufficient to understandconductivity in metals. In the absence of an electric field, these free electrons are moving in random patternswith a mean free speed v. They regularly crash into ion cores (metal ions with the conduction electron(s)missing), then move off again with this same mean free speed.
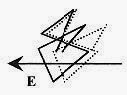
Electric conduction comes about because an electric field is impressed on the metal which slightly modifies this random motion of the electrons giving them a drift velocity in the direction opposite to the field. The accompanying diagram shows the effect of an electric field (dashed lines) on the random motion of a conduction electron in a metal subject to an electric field.
Fig. 29-1
The mean free speed is the speed of the electrons as determined by the temperature of the metal, and the drift velocity is due to the electric field. This drift velocity is small compared to the mean free speed. The motion of the electron charge carriers is characterized by the drift-velocity, the mean free path (the distance between collisions), and the relaxation time (the time between collisions). The drift velocity depends on the applied field. The mean free path and the relaxation time are characteristics of the metal and the physical condition of the metal (temperature, pressure, etc.).
Current
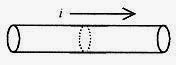
Consider a wire, containing charge, under the influence of an electric field. On a plane through the wire(perpendicular to the charge motion) an amount of charge will pass per unit of time. This is called the current
with unit of ampere = coulomb/second or A = C/s.
Fig. 29-2
The current density is defined as the current per cross-sectional area.
The current direction is direction a unit positive charge would move in the field. Despite the charge being carried by electrons, current is viewed as the motion of positive charge. This definition fits with the previous work in potential.
29-1 A current of 5.0 A exists in a wire of 0.50cm diameter. Calculate the current density.
Solution:
<><><><><><><><><><><><>
29-2 Calculate the amount of charge that passes a cross section each second.
Solution: 5.0 A = 5.0C/s, so 5.0C passes a cross second each second.
<><><><><><><><><><><><>
29-3 Calculate the number of electrons per second.
Solution:
Notice that a current on the order of 10-15 A would amount to 104 electrons per second.
<><><><><><><><><><><><>
29-4 What is the current and current density in a 1.2cm diameter gas discharge tube if 3.0×1017 electrons and2.0×1016 positive ions pass a cross section of the tube each second?
Solution: The current is due to electrons going one way and positive ions going the other way.
The current density is
The amount of charge in a length of wire is the product of number density of charge carriers (number/volume),cross-sectional area, and length (the volume), and the charge per carrier, or
In the presence of an electric field the time for this charge to traverse the length, l, of this volume is the length divided by the drift velocity, t=l/v d. The current is the charge contained in the volume divided by the time for the charges to move the length of the volume. The current is 
and the current density is
29-5 A metal conductor with 2.0×1025 charge carriers/m3 and cross-sectional area 1.0×10-4 m2 has a current of4.0×10-2 A. What is the drift velocity of the charge carriers?
Solution:
Resistance
The resistance of a conductor is defined as the voltage divided by the current, R = V/i and has a special unit,the ohm = volt/amp, or in symbol form Ω = V/A. The resistivity of a material is defined as the electric field divided by the current density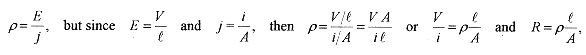
which gives resistivity the units of Ω.m. The resistivity of most metals is the order of 10-8 Ω.m.
The instantaneous relationship between voltage, current, and resistance is
and is known as Ohm’s law. Many metals over a wide range of voltage and current obey Ohm’s law.
29-6 The resistivity of copper is 1.7×10-8 Ω.m. What current flows through a 2.0m long copper conductor of1.0×10-4 m2 cross section when 20V is applied?
Solution: First calculate the resistance:
Now the current:
<><><><><><><><><><><><>
The “free” charge carriers in a conductor experience an electric field when a voltage is applied and this field produces an acceleration a = e E/m, the electric force divided by the mass. The charge carriers accelerate until they crash into an ion core, then the process of accelerate and crash begins again. The characteristic time between collisions, which is dictated by the mean free speed, is called the relaxation time. The accelerationtimes the relaxation time produces the drift velocity.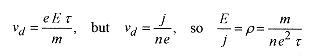
This expression for resistivity is consistent with Ohm’s law. Resistance (and resistivity) is a constant provided the applied field does not change the time between collisions. Remember, the time between collisions is a property of the material and is not appreciably affected by the applied electric field.
29-7 Take a rectangular block of metal 1.0×10-4 m2 in cross section, 50cm in length with a relaxation time of3.0×10-14s. Apply 4.0V for a current of 3.0A. Calculate resistivity, electrons/sec. passing a cross section, current density, the acceleration of the electrons, and the drift velocity.
Solution: The resistivity is 
The number of e–/s passing a cross section is
Calculate the current density.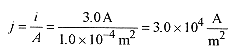
Calculate the acceleration of the electrons.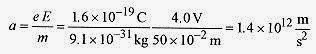
Calculate the drift velocity. v d = a τ=(1.4 × 1012 m/s2)(3.0×10-14 s) = 4.2 × 10-2 m/s
NOTE: The mean free speed, the speed of the electrons before the application of the field, is the order of 106m/s .
Power
In electric circuits, energy is transferred when charge moves under the influence of voltage. Since voltage is work/charge, then the energy involved in moving an amount of charge under the influence of voltage is the voltage times the charge. In differential form
Power (work/time) d U/d t is P = Vi
In a circuit where V, i, and R are related by V = i R this power can be written
In the case of electrons passing through a metal this energy is manifest as heat in the conductor. The energy transfer is known as Joule’s law of heating. The units are VA = (J/C)(C/s) = J/s= W.
29-8 A 1000W electric heater operates at 115V. Calculate the current, resistance, and energy generated in one hour.
Solution: The current in the heater is
The resistance is
The energy generated in one hour is U = P t = (1000J/s) (3600s) = 3.6×106 J.
29-9 For the situation of problem 29-8, if the voltage is reduced to 110V (assume no change in resistance) how does the heat output change?
Solution: This is best handled with a variational equation. In this case start with P = V2/R and ask how does P change with V, while R remains constant. The left side becomes ΔP, and the right side becomes (1/R) times the differential of V2. Writing in delta format 
The 2VΔV is the difference between (V + ΔV)2 and V2.
The ΔV2 term is dropped because it is small compared with 2VΔV. For this case them
What is the fractional change in power output, Δ P/P?
NOTE: The fractional change is the change divided by the original amount.
There is an 8.7% decline in power for a 4.35% decline in voltage.
Temperature Dependence of Resistivity.
The resistance or resistivity of a metal depends on temperature according to 
where α is the temperature coefficient of resistance. This increase in resistance is consistent with our view of electric conductivity as charge carriers moving under the influence of an electric field until they crash into much larger ion cores.
As a metal is heated, energy goes into vibration of the ion cores. Charge carriers moving through the metal have a greater chance of intercepting an ion core as the amplitude of the oscillations increases. More collisions means greater resistance.
As an analog, consider the problem of walking blindfolded across a room with all the same size people stand in gin a random pattern in the room. The number of times you collide with another person depends on the relative cross sections (areas) of you and the people standing in the room. If the people are put into oscillation,perpendicular to your direction of motion, the probability of collision becomes greater. In the time it takes for you to move past each person, they move, increasing the probability of collision. They have a greater effectivecross section, with respect to your walking across the room, because of their motion.
29-10 Calculate the resistance of an iron bar when the temperature is raised from 0°C to 100°C.The initial resistance is 1.43Ω, and the temperature coefficient of resistivity is 0.00501/C°.
Solution:
Batteries and emf
Batteries can be viewed (loosely) as charge pumps. Work is performed on charge as it moves through thebattery effectively raising its potential (energy). This potential energy is expended when a path (circuit) isprovided for the charge to travel outside the battery. The ability of the battery to do work on the charge passingthrough it is called the electromotive force (emf). The electromotive force is measured in volts. A 10 voltbattery can perform 10 Joules of work on each coulomb of charge passing through it and is said to have an emf of 10 V.
A battery connected to a load with resistance, R, causes current to flow in the load according to the V = i Rrelation . For an amount of charge flowing through the load, the drop in potential (voltage) is the same as the gain in potential (voltage) in the battery. This is a conservation of energy statement: the charge does not go faster and faster as it moves around the circuit; neither does it go slower and slower; it moves at a rate dictated by V = iR.
Real batteries have internal resistance. Batteries viewed as charge pumps have resistance associated with moving the charge through the battery. The no load (no current) voltage at the terminals of the battery is the emf of the battery. As current is supplied by the battery, the internal resistance lowers the voltage at the terminals. In circuits, batteries are usually depicted as a voltage source in series with a resistor.
29-11 A battery with an emf of 10 V has internal resistance of 0.70Ω. What is the voltage at the terminals of thebattery when 1.0 A is being drawn by an external load?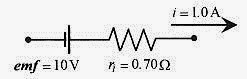
Fig. 29-3
Solution: The voltage drop inside the battery is i ri = 1.0A .0.70Ω = 0.70V, so the output voltage is reduced to9.30 V.
<><><><><><><><><><><><>
When batteries with internal resistance are connected to external loads, the battery plus internal resistance isusually shown enclosed either by a dashed line or shading and the emf specified by the symbol emf.
29-12 A battery of 12 V emf has internal resistance of 0.50Ω and is connected to a 6.0Ω load. What is the terminal voltage of the battery under these conditions and the power dissipated in the external resistor?
Solution: The total current comes from emf = i(ri + R) or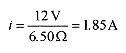
At this current the voltage drop due to the internal resistor is 1.85A.0.50Ω = 0.92 V, so the output voltage orvoltage applied to the 6.0Ω resistor is 11.08V.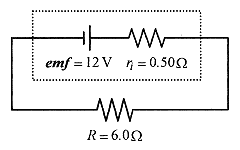
Fig. 29-4
The power dissipated in the external resistor is P=Vi=11.08V.1.85A = 20.5W.