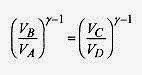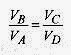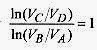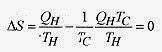Second Law of Thermodynamics
The first law of thermodynamics deals with heat, work, and internal energy. The second law deals with the direction and efficiencies of thermodynamic processes. Many thermodynamic processes proceed in one direction but not the reverse. Applying the brakes to stop a car is an excellent example of a thermodynamic process (the conversion of mechanical energy to heat) that is not reversible.
It is possible to convert mechanical energy into heat with 100% efficiency. It is not possible to convert heat into mechanical energy with 100% efficiency.
Heat Engines
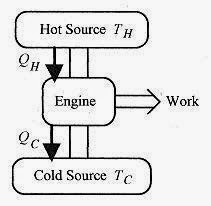
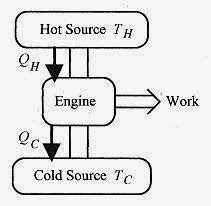
A heat engine is a device that converts thermal energy to other (usually mechanical or electrical) forms of energy. The engine takes a working substance through a cycle where heat is absorbed from a hot source and expelled to a cold source. The cycle may involve taking on or expelling heat, expansion, compression, or a phase change. Figure 20 1 depicts a heat engine extracting heat from a hot source, performing work, and expelling heat to the cold source, In this engine the working substance goes through a cycle so that over one cycle ΔU = 0. In real engines, such as the typical automobile engine, the working substance is the air fuel mixture continuously supplied to the engine. In this case the working substance is not physically the same but has the same characteristics. According to the first law ![]()
The thermal efficiency of an engine is defined as the ratio of the work performed to the heat taken in, or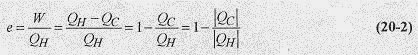
Fig. 20 1
To avoid the confusion of determining the algebraic sign of heat entry or exit of the system, the thermal efficiency, e, is defined with absolute value signs. According to this definition an engine that converted all the heat taken in to work would be 100% efficient.
One way of stating the second law of thermodynamics is to say that: A heat engine cannot have an efficiency of 100%. In terms of the engine, all the heat taken in cannot be converted to work. The first law of thermodynamics says that we cannot get more energy out of a thermodynamic system than we put in, and the second law says we cannot hope to break even in extracting energy (mechanical or electrical) from heat.
20 1 What is the efficiency of an engine that takes in 300J and expels 100J over each cycle?
<><><><><><><><><><><><>
20 2 If an (gasoline) automobile engine performs 10kW of work and is 28% efficient, what is the rate at which heat is taken in and expelled?
Solution: It doesn’t matter whether we take the heat in and the work performed for one cycle or the rates for heat in and work performed. The efficiency is e = W/ QH so the rate of heat in is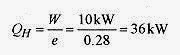
From the efficiency equation 20 2,![]()
Carnot Cycle
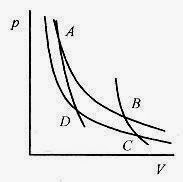
The Carnot cycle or engine operates in an ideal reversible cycle between two temperatures. Figure 20 2 shows the two isothermal and two adiabatic paths for the working substance. For the cycle to be reversible the paths have to be reversible. A reversible path or process is one that can be made to go backwards or forward. The working substance following these isotherms and adiabats can be taken in either direction by changing the conditions. For example, along the isotherm from A to B changing the volume slowly (in either direction) will make the system move up or down the isotherm.
A similar argument holds for the adiabats.
Fig. 20 2
Take an ideal gas as the working substance through a complete cycle.
Path A ¨ B is an isothermal expansion at TH. The gas is placed in contact with a heat reservoir that provides QH while the gas does work in expanding from VA to VB.
This work according to equation 19 3 is![]()
Path B ¨ C is an adiabatic expansion.
Path C ¨ D is an isothermal compression at TC. The gas is placed in contact with a heat reservoir that removes QC while work is done on the gas compressing it from VC to VD.![]()
This work according to equation 19 3 is
Path D ¨ A is an adiabatic compression.
In this (cyclic) process the working substance has been taken from TH to TC and back to TH. The area bounded by these four curves is a visual measure of the inefficiency of the Carnot engine.
The efficiency of the Carnot engine is 1 |QC|/|QH| so form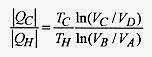
The logarithmic part of this expression can be simplified by looking at the adiabatic relations. The adiabatic processes follow ![]()
and |QC/QH| reduces to TC/TH and the efficiency is 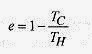
20 3 A steam engine is operated with steam at atmospheric pressure and 100‹C. Steam leaves the engine at slightly above outside temperature, 35‹C. What is the efficiency of the engine?
Solution: e = 1 308/373 = 0.17 E 17%
<><><><><><><><><><><><>
20 4 For the situation of problem 20 3 increase the pressure in the boiler so that the temperature of the steam is 450K. What is the efficiency of the engine?
Solution: e = 1 (308/450) = 0.32 E 32%
<><><><><><><><><><><><>
20 5 A heat engine takes in 2000J of heat and performs 400J of work each cycle. What is the efficiency, amount of heat rejected, and the power output for a cycle rate of 100cycles/s?
Solution: The amount of heat rejected in each cycle is 2000J 400J = 1600J.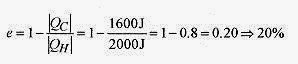
The efficiency is The power output for the engine is 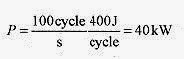
<><><><><><><><><><><><>
20 6 An electric generating plant has an output of 50MW. Steam enters the turbines at 550‹C and exits at 110‹C. The efficiency of the plant is 80% of the theoretical Carnot efficiency. What is the rate of heat consumption and heat rejection?
Solution: The Carnot efficiency is e = 1 TC/TH = 1 383K/823K = 0.53
Eighty percent of this is 43% efficiency. This means that 43% of the input is equal to the 50MW output, giving an input requirement of 116MW. The rate of heat rejection is 57% of the 116MW input or 66MW (rejected).
Refrigerators and Heat Pumps
Refrigerators and heat pumps perform the same function, they supply mechanical energy (work) to an engine that moves heat from a cold place to a hot place.
A heat pump has as its purpose to heat. The measure of efficiency is called the coefficient of performance and is the ratio of heat transferred to mechanical work input. Heat engines take in heat in order to perform mechanical work. Refrigerators and heat pumps take in mechanical energy in order to move heat from a cold to a hot place (opposite to the normal direction of the process). 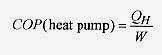
Remember that for a Carnot engine W = QH QC and that QH/QC = TH/TC. For a Carnot engine run as a heat pump the coefficient of performance is
Fig. 20 3
A refrigerator has as its purpose to cool. The coefficient of performance is
For the Carnot engine run as a refrigerator
20 7 What is the coefficient of performance of a refrigerator operating as a Carnot engine between 5‹C and 25‹C?
Solution: COPC(refrigerator) = 278/20 = 14
Most refrigerators run at 1/2 or less of their Carnot efficiencies.
<><><><><><><><><><><><>
20 8 Assuming Carnot efficiency calculate the coefficient of performance of a heat pump operating between 20‹C and 12‹C. Find the minimum power requirements to move thermal energy from the 12‹C area to the 20‹C area at the rate of 20kW.
Solution: The coefficient of performance for a heat pump is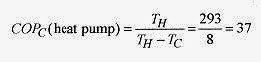
The coefficient of performance is the ratio QH/W so QH/W = 37, or 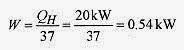
The theoretical minimum power to move the 20kW (from cold to hot) is 0.54kW. Real heat pumps require about twice this theoretical minimum power. Notice, however, that it takes much less power to gmoveh heat than it does to heat directly. In this case about one kW moves 20kW. Heat pumps are most efficient in mild climates. As the temperature difference increases the coefficient of performance decreases.
Entropy
Entropy is a measure of disorder. Since perfect order or perfect disorder is hard to define, the definition of entropy is given in terms of the change in entropy. If a system can be taken over a reversible path at constant temperature then the change in entropy is the heat necessary to traverse this path divided by the temperature, regardless of the path actually taken 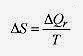
The subscript r is a reminder that the heat transfer is to be measured over a reversible path even though the system may have been taken over an irreversible path.
20 9 What is the change in entropy for 50kg of water going from liquid to vapor at 100‹C?
Solution: The conversion of water from liquid to vapor is reversible, and the heat required is the heat of vaporization of water (3.3~105J / kg), so 
Water vapor has more disorder than water (liquid).
<><><><><><><><><><><><>
20 10 Calculate the change in entropy for 200kg of water slowly heated from 20‹C to 80‹C.
Solution: The basic definition of entropy is ΔS = ΔQr / T. The heating process is surely reversible. Switching to a calculus definition 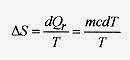
and integrating over the temperature range 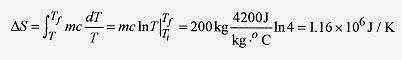
<><><><><><><><><><><><>
Consider the change in entropy during one Carnot cycle. Refer to Fig. 20 2 and the associated discussion of the cycle. Along the isotherm A ¨ B an amount of heat QH is absorbed at TH. Path B ¨ C is adiabatic as is path D ¨ A, so no heat is absorbed or rejected in these paths. Along path C ¨ D an amount of heat QC is expelled at TC so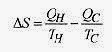
The total entropy change for one Carnot cycle is zero. This is also true for any reversible cycle.