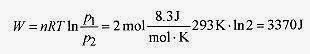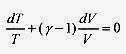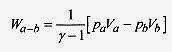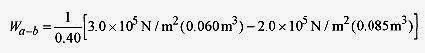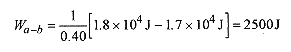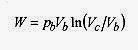First Law of Thermodynamics
The first law of thermodynamics is a conservation of energy statement for thermodynamic systems that exchange energy with their surroundings. It states that energy cannot be created or destroyed, but may only be changed from one form to another. The discussion is restricted to ideal gases and systems with constant mass. The quantity of heat, Q, added to the system and the work performed by the system, W, are taken as positive.
Work During Volume Change
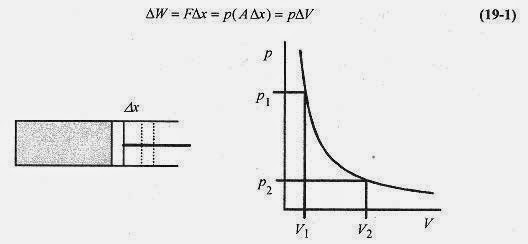
Place a gas in a cylinder with a moveable piston. If the gas is allowed to expand at constant temperature, there is a force on the piston F = pA, and this force acting over a distance Δx is the work performed by the system.
Fig. 19 1
Figure 19 1 shows the cylinder with moveable piston and a p V diagram. The single (p V) curve is an isotherm, a constant temperature curve.
The total work in expanding from V1 to V2 is the area under the p V curve from V1 to V2. This is analogous to a spring where the work to compress the spring is the area under the curve of F vs x (see Chapter 7, Work and the Definite Integral).![]()
The pressure depends on p through pV = nRT. At constant temperature the system follows the curve in Fig. 19 1. Writing p in terms of V 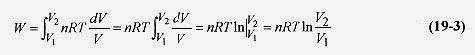
Since the gas is expanding at constant temperature, it is moving along an isotherm (T = const) line so p1V1 = p2V2, and another expression for work is ![]()
19 1 Two moles of an ideal gas maintained at 20‹ C expand until the pressure is one half the original. How much work is done by the gas?
Solution: Since the gas remains at constant temperature, it goes from one state to the other along an isotherm (see Fig. 19 1).
<><><><><><><><><><><><>
19 2 A gas at constant pressure of 4.0 x 105 Pa is cooled so that its volume decreases from 1.6m3 to 1.2m3. What work is performed by the gas?
Solution: Since pressure is a constant the work performed is from equation 19 1. ![]()
The negative sign indicates that work was done on the system by an outside agent.
Internal Energy and the First Law
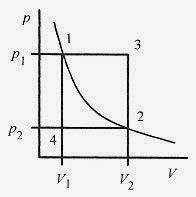
In going from state (p, V, T) to state (another p, V, T) a gas goes through a set of intermediary states. These states are called the path the system takes. On the p V diagram in Fig. 19 2 the point p1V1 represents the initial point and p2V2 the final point.
Fig. 19 2
If the gas were taken along the isothermal line, then the work performed would be the area under the p V curve as shown earlier. Consider, however, two different paths. First, the path from 1 3 2 could be accomplished by expanding the gas at constant pressure (1 3) then reducing the pressure to reach p2. In this case the work performed would be the area under the 1 3 line.
A second path from 1 4 2 is accomplished by reducing the pressure to p2 then expanding the gas to V2. In this case the work performed would be the area under the 4 2 line.
The work performed by the system in going from state 1 to state 2 via the 1 3 2 route is different from the work performed via the 1 4 2 route. Since there are an infinite number of possible routes from state 1 to state 2, the amount of work performed in going from state 1 to state 2 depends on the path.
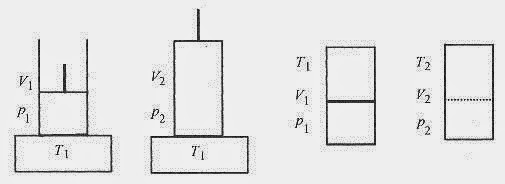
Now consider an ideal gas in a container with a moveable piston and heat source (Fig. 19 3).
The gas atp1V1T1 is heated to a state p2V2T1. Heat is added from the reservoir to change p and V but not T.
The same amount of gas is placed in another container of volume V2, but the gas is confined to V1 with a breakable partition and the space above V1 is evacuated. If the partition is broken, the gas expands to V2 without a change in temperature and sufficiently rapidly so there is no heat transferred in the process. This rapid expansion of a gas into a vacuum is called free expansion. These two extreme routes are illustrative of the infinite number of possible routes, each requiring a different amount of heat, from p1V1T1 to p2V2T1. Therefore, the amount of heat necessary to go from one state to another depends on the path.
Fig. 19 3
While the amount of heat to go from one state to another depends on the path and the amount of work to go between these two states depends on the path, the difference, heat minus work, is independent of the path and always appears as a change in internal energy of the gas. In equation form this is![]()
This last statement is the first law of thermodynamics and in words states that heat into a system appears either as an addition to the total internal energy or work performed by the system. Going from one state to another where the temperature of the state is the same, the heat in equals the work performed. Going from one state to another where the temperature of the state is not the same the heat equals the increase in internal energy plus the work performed.
19 3 You eat 100 food calories worth of nuts. How high would you, at 65kg, have to climb to gwork offh these 100 calories?
Solution: The 100 food calories is 100kcal into your (thermodynamic) system. The work to reduce your total internal energy back to what it was before eating the nuts is ![]()
<><><><><><><><><><><><>
19 4 In a certain process 1.5x105 J of heat is added to an ideal gas to keep the pressure at 2.0x105 Pa while the volume expands from 6.3m3 to 7.1m3. What is the change in internal energy for the gas?
Solution: Apply the first law ΔU = ΔQ ΔW. Since the pressure is constant 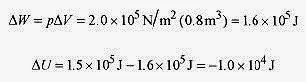
The internal energy of the gas has been decreased by 1.0x104 J.
<><><><><><><><><><><><>
19 5 An ideal gas initially at 3.0x105 Pa, volume of 0.030m3, and temperature 20‹C is heated at constant pressure to a volume of 0.120m3. How much work was performed by the gas? If 80KJ of heat energy was supplied to the gas, what was the change in internal energy?
Solution: The work performed is![]()
The increase in internal energy is![]()
<><><><><><><><><><><><>
There are several different thermodynamic processes that occur often enough to warrant definition.
An isothermal process occurs at constant temperature.
An adiabatic process is one where no heat is transfered in or out of the system (ΔQ = 0).
An isobaric process occurs at constant pressure (W = pΔV).
An isochoric process occurs at constant volume (W = 0).
Heat Capacities of Ideal Gases
The heat capacity of an ideal gas depends on whether the measurement is made at constant volume, CV, or constant pressure, Cp.
At constant volume (ΔV = 0) no work is performed by the system, so according to the first law ΔQ = ΔU. For n moles requiring CV amount of heat per mole![]()
At constant pressure work is performed. Defining the heat capacity at constant pressure as the heat to raise one mole of a gas one degree, ![]()
Since the gas expands in this process, work, ΔW = pΔV is performed. From the ideal gas law pΔV = nRΔT so ΔW = nRΔT. Substituting in the first law in the form ΔQ = ΔU + ΔW, nCpΔT = ΔU + nRΔT. Since the internal energy depends only on temperature ΔU = nCVΔT and ![]()
Measurements on gases confirm this relationship.
19 6 What is the total internal energy of 10 moles of an ideal monatomic gas at 20‹ C?
Solution: A monatomic gas is composed of single atoms that behave as mass points, and as such, they can only translate. They cannot rotate or vibrate. See problem 18 5 and the associated discussion to confirm that the internal energy is (3/2)nRT.
<><><><><><><><><><><><>
19 7 The heat necessary to raise the temperature of 10 moles of an ideal gas at a constant pressure of 1.0 x 105 Pa 10 degrees is 2100J. What is the volume change and the heat capacity at constant pressure and constant volume?
Solution: The work performed in the volume change is ΔW = pΔV = nRΔT so 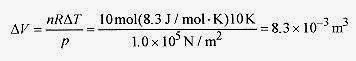
Starting with the basic statement ΔQ = nCpΔT the heat capacity at constant pressure is 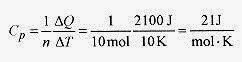
The gas constant R is 8.3 J / mol . K so![]()
19 8 Two moles of an ideal gas at a pressure of 1.0atm has 400 J of heat added in expanding from a volume of 4.7 x 10 3 m3 to 7.0 x 10 3 m3. What is the change in internal energy and temperature? What are the specific heats?
Solution: The work performed is W = pΔV = 1.0 x 105 N / m2 (2.3 x 10 3m3) = 230J.
The change in internal energy is from the first law ΔU = ΔQ W = 400 J 230J = 170J.
The change in temperature is from ΔU = (3 / 2)nRΔT, or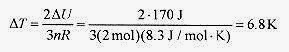
The heat capacity at constant pressure is from ΔQ = nCpΔT, or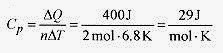
The heat capacity at constant volume is![]()
Adiabatic Processes.
Adiabatic processes are ones where there is no heat transfer between the system and its surroundings. Rapid volume changes where there is no time for heat transfer are characteristic of adiabatic processes.
Fig. 19 4
A model adiabatic process is shown in Fig. 19 4. An ideal gas in an insulated container with a moveable weighted piston rapidly expands when the weight is removed. The volume increases, and the pressure and temperature drop with no heat in or out.
From the first law ΔU = W and ΔU = nCvΔT and W = pΔV. Writing the first law with p replaced from the ideal gas law pV = nRT ![]()
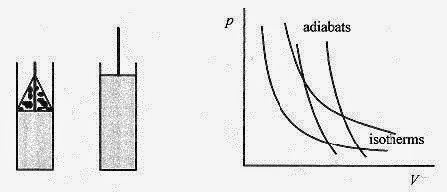
Switching to differential format 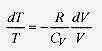
The factor R / CV is usually written in the form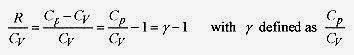
is integrated directly as a logarithm
In T + (ƒÁ 1) InV = In (const), and applying the laws of logarithms TVƒÁ 1 = const
Again applying the gas law pV = nRT, 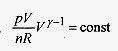
or pVƒÁ = (another) const.
For a monatomic gas ƒÁ = 1.40. For adiabatic expansions there are two relationships ![]()
The p V curves for the pVƒÁ = const are a lot like pV = const curves. The pVƒÁ = const curves are called adiabats and are shown in Fig. 19 4 along with (for comparison) some isotherms.
19 9 Two moles of an ideal gas expand isothermally at 295K from 0.60m3 to 0.80m3. What would be the temperature of the gas if the same expansion were adiabatic?
Solution: The temperature is from equation 19 7.![]()
19 10 Air and fuel at 300K and 1.0atm is compressed in an automobile engine with a compression ratio of 8 to 1. Take ƒÁ = 1.40 and calculate the final pressure and temperature of the mixture.
Solution: The pressure is from ![]()
<><><><><><><><><><><><>
19 11 An ideal gas at 3.0 x 105 Pa and 0.080m3 is compressed adiabatically to 0.020m3. What is the final pressure and the work performed?
Solution: The final pressure is from ,![]()
The work performed is from W = nCvΔT = nCv(T2 T1). Substituting from the ideal gas law pV = nRT and R/Cv = ƒÁ 1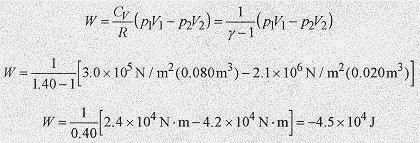
Work is performed on the gas in the amount of 4.5 x 104J.
<><><><><><><><><><><><>
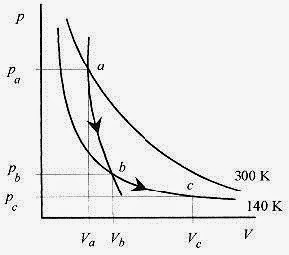
19 12 An ideal monatomic gas at pa = 3.0 x 105 N/m2, Va = 0.060m3, and T = 27‹C expands adiabatically to pb = 2.0 x 105 N/m2, Vb = 0.085m3 and then isothermally to Vc = 0.100m3. What is the final temperature, pressure, and work performed by the gas? Show these paths on a p V diagram.
Solution: First calculate the temperature at the end of the adiabatic expansion using the ideal gas law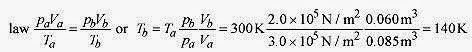
The gas has moved along an adiabat from the 300 K isotherm to the 140K isotherm (point a to point b on Fig. 19 5).
The pressure at the end of the isothermal expansion can be calculated from the ideal gas law with the temperature a constant, PbVb = PcVc, or![]()
The temperature of the gas at point c is 140K, and the pressure is 1.7 x 105 Pa.
The work performed is positive in both parts of the expansion. During the adiabatic portion of the expansion, the work is the area under the a b portion of the curve (see problem 19 11).
Fig. 19 5
In the isothermal portion of the expansion the work is the area under the b c curve (equation 19 3).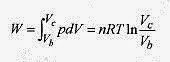
This is the work performed in the isothermal expansion. Along the isotherm pbVb / Tb = pcVc / Tc reduces to pbVb = pcVc because Tb = Tc.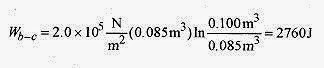
The total work performed by the gas is 5260J.
Look over this problem again. It is probably the most difficult one you will encounter, and if you understand all the steps and can do them on your own, you understand the first law of thermodynamics very well.