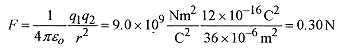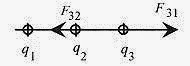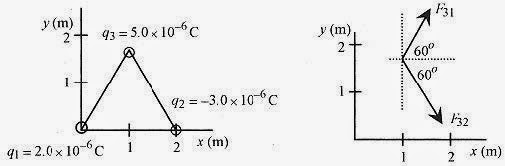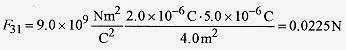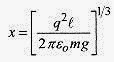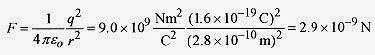Charge and Coulomb’s Law
Coulomb’s law is the basic force relationship between two charges. This force acts along the line connecting the charges and is repulsive for like charges and attractive for unlike charges. ![]()
where ƒÃo = 8.9 x 10 12 C2/Nm2 , and ![]()
The proportionality constant can, for the moment, be thought of as a constant that makes the force Newtons when the charges are measured in Coulombs and the separation in meters.
24 1 Two charges, q1= 3.0x10 8C and q2 = 4.0x10 8 C, are separated by 6.0x10 3 m as shown in Fig 24 1. What is the force of one on the other?
Solution:
Fig. 24 1
This is the force each charge experiences due to the other. The fact that q1 is positive and q2 is negative means that the force is directed from one to the other along the line joining their centers.
<><><><><><><><><><><><>
24 2 Consider a line of charges, q1 = 8.0μC at the origin, q2 = 12μC at 2.0 cm, and q3 = 10μC at 4.0cm, as shown in Fig. 24 2. What is the force on q3 due to the other two charges?
Solution: The force on q3 due to q1 is repulsive as shown in Fig. 24 2. The magnitude of F31 is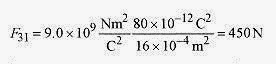
Fig. 24 2
It is not necessary to be overly concerned about the sign of the force. The vector makes the direction clear. Drawing a vector diagram is a more sure way of getting the final direction correct than using algebraic signs in the force calculations.
The force on q3 due to q2 is attractive, and the magnitude is 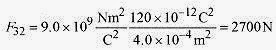
The resultant force is 2250N toward q1 and q2.
<><><><><><><><><><><><>
24 3 Arrange three charges in the form of an equilateral triangle as shown in Fig. 24 3 and find the force on q3 due to the other two.
Fig. 24 3
Solution: This is a more complicated vector problem. First calculate the force on q3 due to q1 and then due to q2. Adding these vector forces is called superposition. The forces can be added as vectors as long as the force due to one charge does not affect the force due to another charge. In this case the force on q3 due to q1 does not influence the force on q3 due to q2.
and is directed as shown in Fig. 24 3. Likewise the force on q3 due to q2 is 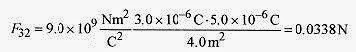
and is directed as shown. Referring to Fig. 24 3, the x and y components of the resultant force can be written. The x component of these two forces is ![]()
The y component of these two forces is ![]()
Second Solution: Using unit vector notation the forces are written as 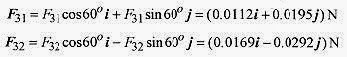
Rather than worry about the algebraic signs of angles other than 0‹ to 90‹ draw the picture and keep the angles under 90‹. This way it is easy to gseeh the sign of the various components. Most mistakes in problems like this are algebraic sign mistakes. The way to avoid these mistakes is to draw and label a vector diagram, more than one if necessary.
As an exercise find the magnitude and direction of the resultant.
<><><><><><><><><><><><>
A classic charge problem is one where charged balls are hung by strings from a common point with the question being how far apart the balls separate for a given equal charge.
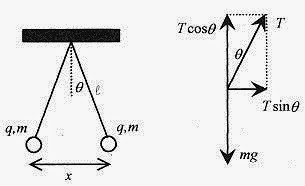
24 4 Consider two conducting balls both of mass m and equal charge q suspended by nonconducting cords of equal length, l as shown in Fig 24 4. How does the separation of the balls depend on charge, mass, and length?
Fig. 24 4
Solution: The arrangement is shown in the accompanying drawing along with the vector diagram. This is a force balance problem. The mechanical force is due to gravity and is directed down. The electrical force is the Coulomb force and is directed along the line of centers of the conducting balls, which for this geometry is horizontal.
On the vector diagram the mg force is balanced by the vertical component of the tension in the cord, or T cosθ=mg. The horizontal component of the tension is T sinθ, and replacing T with mg/cosθ the horizontal component is![]()
But tanθ can be written in terms of the geometry as![]()
The horizontal component of the tension in the cord is balanced by the Coulomb force of repulsion![]()
<><><><><><><><><><><><>
24 5 What is the force of attraction between sodium and chlorine ions in salt molecules if each ion carries one electronic charge and the separation is 2.8 x 10 10 m?