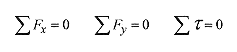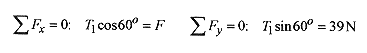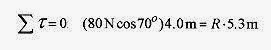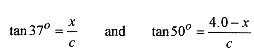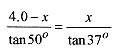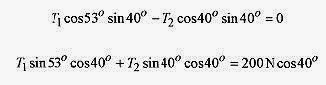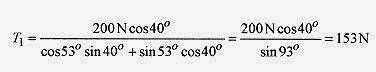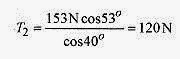Equilibrium
The only difficulty you will encounter in doing equilibrium problems is lack of familiarity with the mechanics of doing the problems. This is overcome by doing problems. The theory is simple. If something is not moving, that is, it is in equilibrium, then the sum of the forces on it must be zero. Likewise if it is not rotating, then the sum of the torques must be zero.
For problems in two dimensions these laws are stated very simply:
We start off with some simple problems requiring force analysis only and progress to problems involving torques.
13 1 Hang a 50kg mass with ropes making angles of 30° and 45° as shown in Fig. 13 1. Calculate the tension in the ropes.
Fig. 13 1
Solution: Note that all the forces come together at the knot in the rope so draw a force diagram about this point. The only laws to apply are for equilibrium in the x and y directions.
This provides two equations in two unknowns. Because sin45° = cos45° rewrite
and
As an exercise work through this problem with different angles.
<><><><><><><><><><><><>
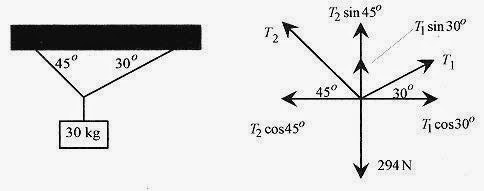
13 2 In the arrangement shown in Fig. 13 2, what is the minimum coefficient of friction to prevent the 8.0kg mass from sliding?
Fig. 13 2
Solution: The forces come together where the cords come together. This point is not moving so apply the equilibrium conditions here. The vector diagram at this point is also in Fig. 13 2.
The equilibrium conditions are:
Solving for T1:
The force is: F=45N cos60° = 22.5N
This force is supplied by the frictional force ìmg, so
This is the minimum coefficient of friction that will prevent me system from moving.
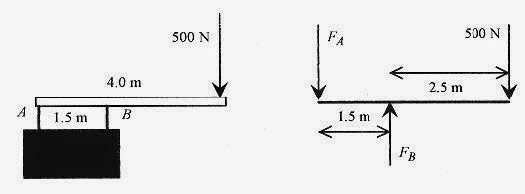
13 3 A 500 N diver is on the end of a 4.0m diving board of negligible mass. The board is on pedestals as shown in Fig. 13 3. What are the forces that each pedestal exerts on the diving board?
Solutions: There are no forces in the x direction, but in the y direction the pedestal at A and the diver are acting down while the force at pedestal B is acting up. Pedestal B is in compression while pedestal A is in tension. Draw the vector diagram and write the equations.
Fig. 13 3
In this problem apply 
about pedestal A. Taking the rotation point at pedestal A, the diver produces a clockwise torque, and pedestal B an anti clockwise torque that are in equilibrium. Note that this is not the only possible rotation point.
Solve for FB:
Solve for
As an exercise write the
about pedestal B and the diver.
<><><><><><><><><><><><>
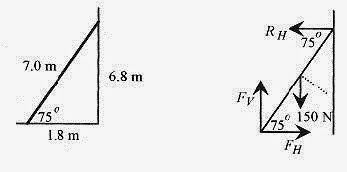
13 4 Place a 7.0m uniform, 150N ladder against a frictionless wall at an angle of 75°. What are the reaction forces at the ground and wall and the minimum coefficient of friction of the ground?
Solution: Figure 13 4 shows the ladder with the 150N acting down at the center of the ladder and the sides of the triangle formed by the ladder, wall, and ground. The vector portion of the figure shows the two components of the reaction force at the ground. The reaction force at the ground is not necessarily in the direction of the ladder. This (vector) force can be written in terms of a force (magnitude) at an angle (with horizontal and vertical components) or directly in component form as done here. Writing the force in component force helps to avoid the temptation to place the force at the same angle as the ladder. Either way requires two variables. Since the wall is frictionless, the reaction at the wall is entirely horizontal. Refer to Fig. 13 4 and write the equilibrium conditions.
Fig. 13 4
The torque on the ladder is taken about the point where the ladder contacts the ground. Note that this choice eliminates two variables from the torque statement. Torque is the (component of the) force at right angles to the lever arm times that lever arm. The 150N weight has a component 150Ncos75° times 3.5m. The reaction at the wall has a component RHcos15° times 7.0m so the sum of the torques equal zero statement is
so
FV and FH are related via the coefficient of friction, FH = μFV so μ = 20/150=0.13
Second Solution: There is another way to calculate the torques. Notice that the 150N force is horizontally 0.90m away from the pivot point. If the 150N force vector is moved vertically so its tail is on a horizontal line from the pivot point, then the torque is easily written as (150N)(0.90m). A similar operation can be performed on RH yielding a torque RH(6.8m). Vectors maintain their length (magnitude) and orientation (angle) but can be moved about a vector diagram for (our) convenience. If the torque statement is written in this way it is identical to the torque statement in the first solution.
As an exercise redo the problem with a person of known weight positioned a specific distance up the ladder.
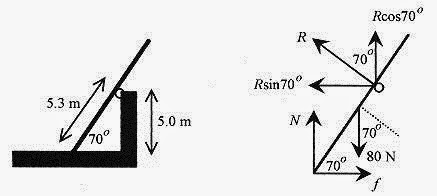
13 5 Place an 80 N ladder 8.0m long on a floor and against a frictionless roller on a 5.0m high wall. The minimum angle for equilibrium is 70°. Find the coefficient of friction between the ladder and the floor.
Solution: The roller is free to rotate so the reaction force is normal to the ladder. This reaction force can be viewed as having vertical and horizontal components. The reaction force at the floor is written as vertical and horizontal components. The geometry and vector diagram are shown in
Fig. 13 5. The length to the roller is obtained from the geometry: sin 70° = 5.0m/L or L = 5.3m
Fig. 13 5 
Write the force equilibrium equations.
The torque about the point on the floor is produced by the reaction force at the roller and the weight of the ladder taken at its midpoint.
Rewriting with f = μN
Solve these equations from last to first to obtain
<><><><><><><><><><><><>
13 6 A 20kg beam 4.0m long is pivoted at a wall and supported by a cable as shown in Fig. 13 6. What is the force at the wall and the tension in the cable?
Solution: There are two points of possible confusion in this problem. First, the mass of the beam is taken as down at the center of the beam. Second, the reaction of the wall, at the pivot, has two components, one up the wall (holding the end of the beam up) and one out of the wall (keeping the beam from sinking into the wall).
Fig. 13 6
Set up the vector diagram at the pivot and the point where the cable is attached. The reaction at the wall is shown with components up the wall and normal to the wall. The weight of the beam is shown as down and from the center of the beam with a component at a right angle to the beam. The tension in the cable is broken up into vertical and horizontal components (for the sum of the forces laws) and a component at right angles to the beam (for the sum of the torques laws). Applying the sum of the forces laws means looking at the vector diagram and adding up all the vectors in the horizontal or vertical directions.
In applying the sum of the torques, it is convenient to take the pivot point at the wall. Since the angle è is unknown, the least complicated sum of the torques statement will come from the tension in the cable and the weight of the beam.
Using the components at right angles
4.0m = 160N. 2.0m
Solve the last equation for the tension in the cable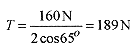 
Use this value to solve for
Now divide these two equations 
and finally, R is obtained from one of the original equations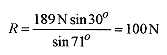
The main points in this problem are the detailed vector diagram and the choice of the wall as the pivot point in calculating the torques.
<><><><><><><><><><><><>
In the early problems, construction of the vector diagram was confined to one point where the forces all “came together.” In problems where there is a strut or ladder or some other extended object the common mistake is to miss a force or torque and have an incomplete vector diagram.
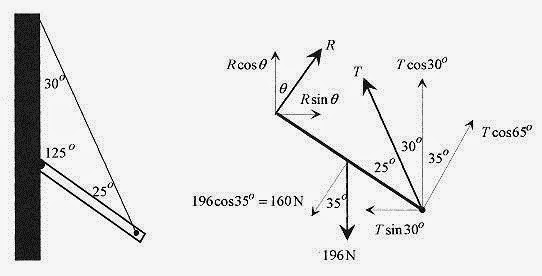
13 7 Set up a 300N strut 14m long with a cable as shown in Fig. 13 7. Find the tension in the cable and the reaction force at the pivot.
Solution: The reaction force at the pivot is set up with vertical and horizontal components. The weight of the strut is taken at the center of the strut with the 2000 N weight at the end. The tension is written along with all the components needed to write the force and torque equations.
Fig. 13 7
Apply the sum of the forces laws.
Apply the sum of the torques law about the pivot point. 
Note that the length of the strut does not influence the calculation.
Solve the torque equation for T.
Use this value to find FH and FV.
The reaction at the floor can be written in terms of magnitude and angle.
<><><><><><><><><><><><>
Another feature of equilibrium problems is that an object hung by two cords has its center of mass along a vertical line determined by the (extension of) intersection of those cords. The argument is based on the fact that a body hung by a cord has its center of mass along the extension of that cord. If the center of mass were not on this line, a torque would exist and the body would move. Likewise if the center of mass were not on the intersection of the two cords, a torque would exist and the body would move.
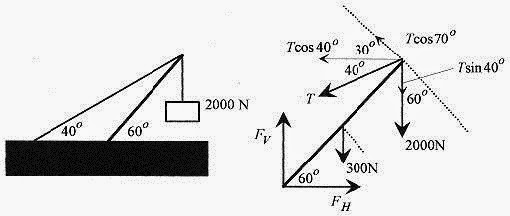
13 8 Consider a non uniform bar of 200N weight and 4.0m length suspended horizontally between two walls where the angles between the walls and cables are 37° and 50°. What are the tensions in the cables?
Solution The extensions of the cables specify the center of mass. Looking just to the center of mass and using the common side of the triangle write
Fig. 13 8
Solve for C and set equal
and 4.0 tan tan° x tan 37° = x tan 50° or
Draw a vector diagram at the center of mass line. Write the equilibrium conditions as
Rewriting
Multiplying and adding
and
A sum of two angles trigonometric identity (see the Introduction, Mathematical Background) was used in the denominator.
