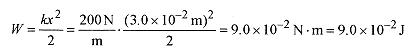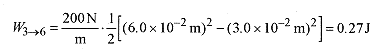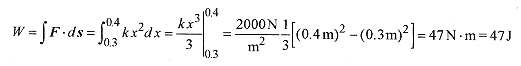Work and the Definite Integral.
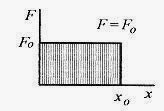
Work is defined as the force, in the direction of a displacement, times that displacement. Consider the application of a constant force, F, applied over a distance, x, as depicted in Fig. 7 -1.
Fig. 7 1
According to the definition, the work is
which is seen as the shaded rectangular area in Fig. 7 1. In calculus terminology the work is the area under the curve. The area under this curve is the area of the rectangle, Foxo. The unit of work is the Joule. (J = N.m)
7 1 Calculate the work performed by a constant force of 60N acting in the direction of a displacement of 3.0m.
Solution:
Fig. 7 2
The force is acting in the direction of the displacement, so the work is the product of force times displacement.
In problem 7 1 the force is in the direction of the displacement, and the work is simply the product of force and displacement. In this next problem the force is not in the direction of the displacement. The simplest way to obtain the component of the force in the direction of the displacement is to form the dot product of force and displacement. Using s as a general symbol for displacement, work is defined as the dot product of the force vector times the displacement vector.
Work is a scalar, the dot product of force and displacement. See the Introduction, Mathematical Background, for a discussion of the dot product.
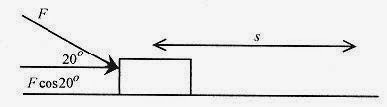
7 2 Calculate the work performed by a constant force of 40N pushing a block a distance of 3.0m along a horizontal surface at an angle of 20‹ with the horizontal as shown in Fig. 7 -3.
Solution: The work performed is calculated with equation 7 2.
<><><><><><><><><><><><>
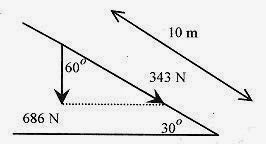
Calculate the work done by the force of gravity acting on a 70kg student sliding down a 30‹ inclined slide a slant distance of 10m.
Solution: The first thing to calculate is the force due to gravity, mg, which is 70kg.9.8m/ s2 = 686 N. Place this vector on Fig. 7 4 pointing down.
Calculate the force in the direction of the incline F = 686N cos60‹ = 343N
The work performed by the gravitational force is W = F.s = 343N.10m = 3430J
<><><><><><><><><><><><>
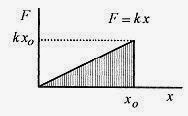
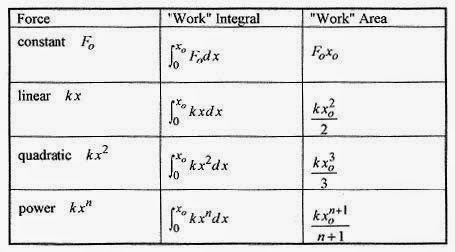
Now consider variable forces and look first at a force that is proportional to x, the displacement, or F =kx where k is a constant. This form of force is encountered in springs where one unit of force compresses (or elongates) the spring a certain distance and the next unit of force doubles the compression, and so on. The graph of force versus displacement is shown in Fig. 7 5.
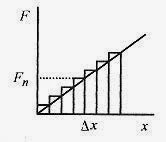
The area under any curve of force versus distance can be approximated by taking a sum of forces times increments of distances over the curve. In this instance take each increment as Ģx and the associated forces as F1,F2,F3c up to N forces and increments as in Fig. 7 6. In mathematical language this sum of the forces would be written as
where F represents the N discrete forces measured at intervals of Ģx from 0 to x0. This sum is a collection of rectangles of height F1, F2,cFN and width Ģx.
Better approximations are obtained by increasing the number of intervals (decreasing the width of each one). In the limiting case the area would be written as
which is a statement that says as Ģx 0 the rectangles become progressively narrower.
Geometrically this limit of the sum represents the garea under the curveh between x = 0 and x = xo and physically represents the work performed by this linear force over x. For a linear spring then the work performed is the shaded triangular area in Fig. 7 5 (1/2 base ~ height) or
Calculate the work performed in compressing a spring with a force constant of 200 N/m the first 3.0cm.
Solution: The work performed is calculated with equation 7 5 as
<><><><><><><><><><><><>
7 5 Calculate the work performed in compressing the spring of problem 7 4 the next 3.0cm.
Solution: The general expression for the work performed is kx2 /2. The work to compress the spring from 3.0cm to 6.0cm is the work to compress it 6.0cm less the work necessary to compress it 3.0cm.
<><><><><><><><><><><><>
This process of taking an infinite number of sums of infinitesimally small increments as described in equation 7 4 and Fig. 7 6 defines an integral.
For the linear or Hooke’s law spring where F = kx the integral becomes
which corresponds to the area under the curve of kx in the interval from 0 to x0.
The area is the area of the triangle and is equal to kx2o/2. We will not develop the general technique for obtaining integrals of power law functions. We will, however, present a justification for the general formula for power law integrals. Consider the following table.
The first two entries in the table are based on the area of a rectangle and a triangle, easy examples done above. The third entry, for the quadratic, follows the pattern of the previous two and can be verified by “numerically” integrating the quadratic, that is, by taking small increments and calculating the associated force and multiplying to find the area of each little approximating rectangle. See the section on integrals in the Introduction. Mathematical Background, for more on this technique. This process also can be done for higher power curves to come to the conclusion shown in the last entry in the table, the one for the general power law curve.
We come now to another definition of work as the integral of the dot product of force and differential distance.
Most of the situations encountered in the elementary course are for constant or linear forces. The linear force is encountered in springs. Linear springs are characterized by the constant, k. The k in the equation F = kx has the units N/m. The work performed in compressing a “kx” spring is kx2 /2. As a final problem consider the work performed in compressing a “quadratic” spring.
7 6 What is the work performed in compressing a quadratic spring, F = kx2, with k = 2000N/m2, from 0.30m to 0.40m?
Solution: The force is in the direction of the displacement so equation 7–8 reduces to
<><><><><><><><><><><><>
Go back through this chapter and notice the development of the definition of work. The first definition was the product of the force in the direction of displacement times displacement (equation 7 1). In order to handle forces not in the direction of the displacement the dot product was introduced (equation7 2). Finally, for nonconstant forces the integral was introduced giving the last definition (equation 7–8).