Binary Representation of Characters

Binary Representation of Characters

When characters are transmitted or stored each character is represented as a binary string. The number of bits used to represent each character differs from one system to another. On punched cards there were 12 hole positions for each character, and on some paper tapes there were only 5. In most modern systems, seven, eight or nine bits are used.

In general the number of different characters which can be encoded is 2ⁿ, where n is the number of bits used for each character.

e.g. The number of different characters you can have with an eight-bit code is 2⁸ = 256.

Worked question

Eight-bit storage locations are used to store coded characters. One bit is a parity bit. 0000 0000 and 1111 1111 both have special uses and cannot be used to code characters. How many different characters can be represented?

Seven bits are used for the actual code.

Seven bits gives 2⁷ = 128 characters.

Two codes cannot be used

No. of possible characters = 128-2

=126

COMMONLY USED CODES

There are many different character codes in use. Which one is used in a particular situation depends on:

1- The size of the character set being represented.

2- The number of bits available for the codes.

3- The medium being used.

Three codes commonly used in computing (Fig 4) are:

1- ASCII-American Standard Code for Information Interchange

2- BCD-Binary Coded Decimal

Fig. 4 Character codes

EXAMPLE-CODES ON MAGNETIC TAPE

1- Audio cassettes

Standard tape cassettes are often used as a backing store for microcomputers. Characteristics

(a) Often only one track is used, one bit lasting a given time interval, bits being stored one after another along the tape.

(b) Usually 1 and 0 are represented by sounds of two different frequencies.

(c) The code used is often ASCII, with ‘start’ bits and ‘stop’ bits in between the characters to show where each character begins and ends.

2- Standard 1/₂-inch computer magnetic tape

Often in reels 732 metres (2400 ft) long as:

(a) a seven-track tape using BCD code and a parity bit; or

(b) a nine-track tape using EBCDIC and a parity bit.

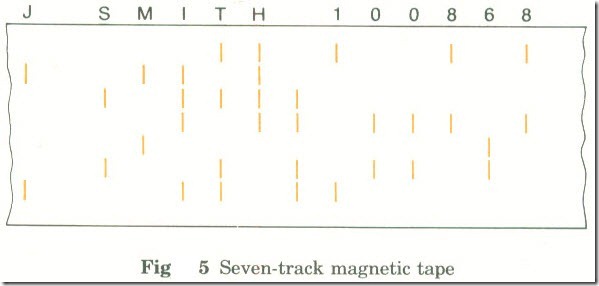
Small areas of the tape are magnetized to produce a situation comparable with paper tape (Fig. 5).

Fig. 5 Seven-track magnetic tape

Note: For further details of storage of data on magnetic tapes, and for details of data storage on discs see Unit 9.2.

Worked questions

1- Suggest, with reasons, two codes which could be used-one for each of the following situations.

(a) A language with a character set of 47 characters is to be used in a computer with a 24-bit word.

(b) In a microcomputer 100 different characters are used and the code must include information as to whether a character is to be printed on the screen normally or in reverse.

(a) 6 bits can hold 2⁶ = 64 different characters

5 bits can only hold 2⁵ = 32 different characters

:. 6 bits are necessary to code 47 characters

BCD code could be used with 4 characters in each 24-bit word.

(b) 7 bits can code 27 = 128 different characters

6 bits can code 2⁶ = 64

:.7 bits are needed to code 100 characters

Seven-bit ASCII could be used. An eighth bit could be 1 for normal printing, 0 for reverse.

2- A computer has a store of 20K 16-bit words. How many characters can be stored in it using an eight-bit character code?

Number of words = 20K

:.Numbers of characters (stored two to a word) =20Kx2

40K

3- When printed in decimal a seven-bit code gives the value 65 for letter A and 67 for letter C.

Suggest values for B and D.

6510= 1000001₂; 6710= 1000011₂

This is probably ASCII. In any case the right-hand digits seem to be the binary for the position in the alphabet (1 for A, 3 for C).

The first bit is not a parity bit. Assume it is 1 for all letters.

Probable codes are B = 1000010; D = 1000100