The V-Curve of a Synchronous Generator

The V-Curve of a Synchronous Generator

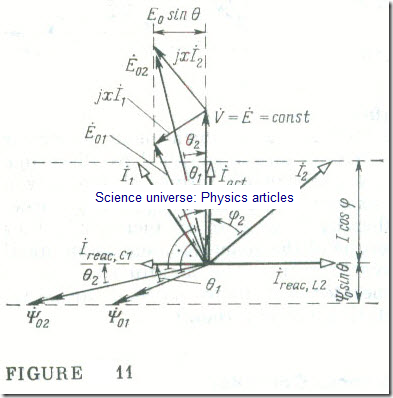
A valuable property of a synchronous generator operating into a large power system is that its reactive current can be controlled by varying its excitation current. For a better understanding of the matter, let us turn to the phase phasor diagram of a synchronous generator (see Fig 8) and analyse it from this point of view (Fig 11) . If the power developed by a synchronous generator, P = ɷ_rotT_em, and the voltage across the system busbars, V, are con­stant, then the products of the terms in Eq. (15.10)

I cos φ = I_act = const (15.14)

E₀ sin │θ│ = ɷ Ψ₀ sin │θ│ =const

are independent of the excitation current. However, a change in the excitation current brings about a change in the associated flux linkage with the stator phase winding, Ψ̇₀ , and in the emf Ė₀ induced by this flux linkage in the phase winding.

It follows from the equation of- electric state of a stator phase, Eq. (15.8), that this can happen only if there is a proportionate change in the phase current

İ= İ_act + İ_reac

or, to be more exact, in the reactive current, İ_reac .

When the excitation current is less than some limiting value,

I_f < I_f,Ifm (P), the current in a capacitive reactive compo­nent, I_reae,_c . When the excitation current is grea­ter than some limiting val­ue, I_f > I_f,_1fm, the current in a synchronous ge­nerator contains an induc­tive reactive component, I_reae,L (Fig. 11). The phase angle respectively is φ < 0 and φ > 0 . In con­sequence, underexcitation makes the reactive power of a synchronous generator capacitive in its effect,

Q_C = 3VI_reac,_c

and overexcitation makes it inductive in its effect

Q_L = 3VI_reac,L

If a synchronous generator operates into a large power system with V = const, its equivalent circuit may be drawn up as a parallel combination of two current sources, one being a source of active current which depends on the torque developed by the prime mover, I_act = f (T_pm), and the other being a source of reactive current which depends on the torque developed by the prime mover and the excita­tion current, I_reac = f (I_f, T_pm).

In the special case of a zero prime-mover torque, T_pm = 0, the phase equivalent circuit of a synchronous generator operating into a large system will contain no active current source, and the reactive current will be solely dependent on the excitation current,

I_reac = f (I_f)·

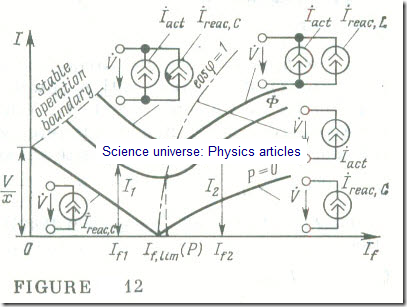
The plots of the current of a synchronous machine operating into a large power system with V = const, as a function of the excitation (field) current, I = f (I_f), at a constant prime-mover torque; T_pm = const, are called the V-curves of the machine (Fig. 12) . At some low value of excita­tion current the angle │θ│(see Fig 10) may exceed π/2 in value, and the sta­bility of the machine may be upset. The greater the active power of a synchro­nous generator, the greater the excitation current at hich the machine may lose its stability. In Fig 12 the boundary of stable operation for a synchronous generator is shown by a dashed line .

The torque developed by the prime mover is zero, T_pm = 0, then, on neglecting all forms of loss, we may take it that the current in a synchronous generator is purely reactive (see Fig 12, P = 0) :

İ (I_f) = İ_reac (I_f) = (Ė – V̇)/j = (jɷΨ̇₀ (I_f) – V̇)/j (15.15)

Now the generator current is a linear function of the excitation cur­rent. The function I = f (I_f) ceases to be linear only at high values of excitation current owing to the saturation of the magnetic circuit of the machine.