External Characteristics of a Transformer

External Characteristics of a Transformer

Consider the performance of a transformer for several values of the complex load impedance Z₂ = z₂ ∠ φ₂ If the primary voltage is constant and equal to its rated value, V₁ = V_1.rtd,variations in the complex load impedance will bring about changes in the primary and secondary currents İ₁ and İ₂ and in the secondary voltage V̇₂ of the transformer.

The difference between the no-load and full-load secondary volt­ages expressed in terms of the former, with the primary voltage held constant, is called the voltage regulation of a transformer. To find it, it is usual to refer (transfer) the secondary voltage to the primary side. Then, V’₂ = (w₁/ w₂) V₂ . The no-load secondary voltage is practically equal to V₁,_rtd Therefore, we may write V₁,_rtd – V‘₂ . Ordinarily, the voltage regulation of a transformer is expressed as a percentage of the rated primary voltage

From the simplified equivalent circuit diagram of a transfor­mer (see Fig. 17 a) and from its phasor diagram (see Fig. 17 b) it follows that

V₁,_rtd – V’₂ ≈ (r_sc cos φ₂ + _sc sin φ₂ ) I₁

or, by Eq. (8.20),

ΔV% = ( I₁ / V_1,rtd) (r_sc cos φ₂ + _sc sin φ₂ ) X 100% (8.21).

A plot of voltage regulation as a function of the load power fac­tor, cos φ₂ , for I₁ = const, is drawn up in Fig.18 a . The voltage regulation is a maximum when cos φ₂ = cos φ_sc , in which case the internal voltage drop phasor Z_scI₁ is in the same direction as the primary voltage phasor VI (see Fig.17 b). In consequence,

V‘₂ = V₁ – Z_scI_l

By plotting variations in the secondary voltage V₂ as a function of the load current I₂ for a constant load power factor and the rated primary voltage, we obtain what is known as the external characteristic of a transformer. As often as not, the external characteristic

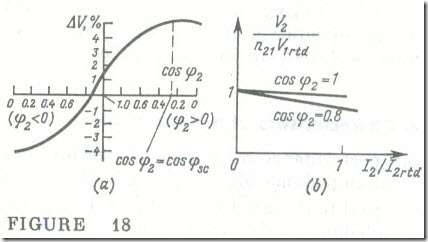of a transformer is constructed on a per-unit basis, that is, in terms of the ratio of the secondary voltage to its rated value, V₂._rtd = n₂₁V₁,_rtd in the open-circuit condition, and its load current ratio

k_load = I₂/I_2.rtd (8.22)

where I₂._rtd = I₁._rtd /n₂₁ is the load current at the rated primary current I₁ = I₁._rtd In view of Eqs. (8.20) and (8.21), the external characteristic of a transformer on a per-unit basis is defined by the following equation

V₂/n₂₁V_{l. rtd} = (1- ΔV %/100) = 1-k_load (I_{1. rtd}/V_{1. rtd})

                           X (r_sc cos φ₂ + _sc sin φ₂)

For φ₂ > 0, the external characteristic is shown in Fig. 18 b.