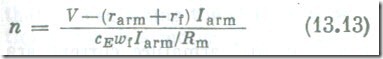The Series Motor
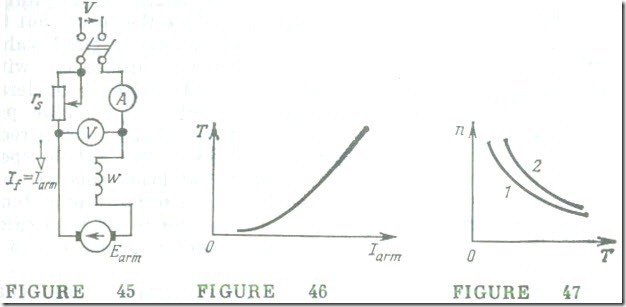
In a series motor the armature current is at the same time its field current, because the field winding is connected in series with the armature winding (Fig. 45). Owing to this connection the main magnetic flux of the machine varies III direct proportron to the armature current so long as the magnetic circuit is not saturated. As is the case with all d.c. motors, series motors are fitted with a starting rheostat, rs .
The emf and torque equations developed for d.c. machines, Eqs, (13.1) and (13.2), can be re-written for the series motor as follows. So long as the magnetic circuit of a series motor is not saturated,
its magnetic flux is directly proportional to the field mmf, .I armwf, and inversely proportional to the reluctance of the machine, Rm
Φ = Iarmwf/Rm
On substituting the above expression into the torque and speed equations of d.c. motors, we obtain the speed equation (the speed-vs-armature current characteristic)
and the torque equation
T = cTwfI2arm/Rm (13.14)
of a series motor.
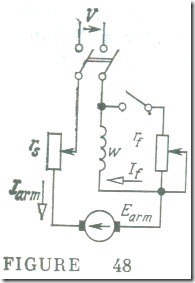
Equation (13.14) shows that the torque of. a series motor with its magnetic circuit unsaturated increases in direct proportion to the square of armature current. Because of this the initial portion of the torque characteristic is a parabolic curve (Fig. 46). When, however, the magnetic circuit is strongly saturated, the flux all but ceases to rise with increasing excitation current, and the torque rises approximately in proportion to the first power of armature current. The speed of a series motor falls off nearly in inverse proportion to current until magnetic saturation becomes noticeable. The natural speed-vs-torque-characteristic of a series motor is shown in Fig. 47 (curve 1). As the load on the motor shaft is increased, the current rises at a relatively low rate, and the speed decreases in inverse proportion to the current. If we neglect the saturation of the magnetic circuit and armature reaction, it may be taken that doubling the torque will cause the current to rise to 140% of the initial value and the speed will drop to 70%. In the case of a shunt motor, doubling the torque would only slightly reduce the speed, but the current would rise to twice the original value. Thus, a series motor is capable of withstanding heavy overloads, with a moderate increase in current which is a valuable property. As the load applied to its shaft is reduced, its current decreases slowly, but the speed goes up rapidly so that at loads smaller than 25% of the rated value a series motor tends to run away with most detrimental consequences to its mechanical integrity. This is the reason why a series motor ought not to be started at no or small load.
Thus, a series motor has a falling (or drooping) speed-torque characteristic because a change in torque has a strong effect on its speed.
The speed of a series motor can be controlled by connecting a field rheostat, rf, across the field winding (Fig. 48). The resistance placed across the field winding brings down the magnetic flux Φ with the result that, in: accord with Eq. (13.11), the speed of the motor, n, increases in inverse proportion to the flux. At the same time, the armature current goes up because the torque is assumed to be constant
T ≈ Φ Iarm
Thus, if the original magnetic flux and armature current are Φ1 and I arml , and as a result of speed control they are Φ2 and I arm2 , then
ΦIarml = Φ2Iarm2
Curve 2 in Fig. 47 is the resistance-controlled speed-torque characteristic of a series motor, that is, one plotted when the field winding is shunted by a fixed resistor, rf.
Another form of speed control is by varying the armature terminal voltage. However it is uneconomical because the armature has to be connected in the series with a rheostat . this from of speed control is used only when the speed has to be reduced by a large amount but for a short time .
the high overload capacity and the falling speed-torque characteristic of series motors suitable for driving hoists and cranes, for traction and rope haulage.