Equivalent Circuits

Equivalent Circuits

The voltage gain of a transistor amplifier can be calculated using an equivalent circuit, or model, of the transistor. An equivalent circuit is one that behaves in exactly the same way as the device it represents. Two equivalent circuits are often employed for audio-frequency amplifier calculations; these are the h parameter circuit and the mutual conductance circuit.

h Parameter Circuit

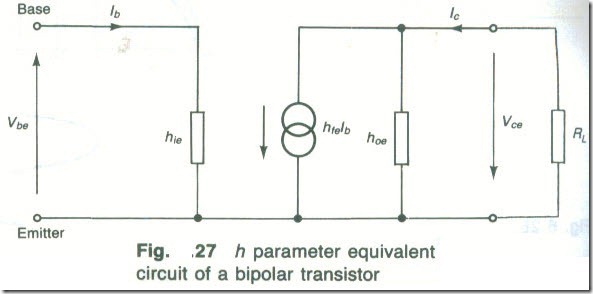
The h parameter equivalent circuit of a bipolar transistor is shown by Fig. 27. The three h parameters have been met previously. h_ie is the input resistance with V_CE constant, h_fe is the current gain with V_CE constant, and h_oe is the output admittance with 18 constant.

When a collector load resistance R_L is connected across the output of the equivalent circuit it will appear in parallel with the output resistance 1/h_oe of the transistor 10 give an effective load resistance R_L(eff) of(R_L x 1/h_oe)/( R_L + 1/h_oe). The collector current I_c= h_feI_b flows in the total resistance to produce the output voltage V_out = V_ce . Therefore

V_out = h_fel_b X R_L(eff)

Very often I/h_oe is much larger than R_L so that R_L(eff) ≈ RL which means that h_oe can be neglected. The input voltage is V_IN = V_be = I_bh_ie so that the voltage gain A_v is

Av = V_out/V_in = (h_feI_bR_L)/I_bh_ie) = (h_feR_L)/h_ie                            (6.11)

Fig. 27 h parameter equivalent circuit of a bipolar transistor

Alternatively, the presence of the collector load resistance reduces the current gain of the transistor to a value less than h_fe . Applying Kirchhoff’s law to the collector circuit:

I_C = h_feI_b + h_oeV_ce                                 (6.12)

An increase in Ic produces an increased voltage drop across the collector resistance and so V_ce falls. Therefore, V_ce = – I_cR_L . Substituting into equation (6.12) gives

I_c = h_feI_b – h_oeI_cR_L

I_c(1 + h_oeR_L) = h_feI_b

I_c = h_feI_b/(1 + h_oeR_L)

Therefore, current gain A_i = I_c/I_b = h_fe/(1 + h_oeR_L )                               (6.13)

Example 12

A bipolar transistor has the following h parameters: h_ie = 1200 Ω , h_fe = 150. and h_oe = 60 X 10^-6 S. The transistor is used as an amplifier with a collector load resistance of2000 O. Calculate the voltage gain of the circuit (a) taking s; into account. and (b) neglecting h_oe.

Solution

(a) Output resistance = 1/h_oe = 1/(60 x 10^-6) = 16.67 kΩ Effective load resistance = 16.67 kΩ in parallel with 2 kΩ, i.e. 17670 Voltage gain = (150 x 1767)11200 = 221 (Ans.)

(b) Alternatively. AI = 150/(1 + 60 x 10^-6 x 2(00) = 134 Voltage gain = (134 x 2000)11200 = 223 (Ans.)

Voltage gain = (150 x 2(00)/1200 = 250 (Ans.)

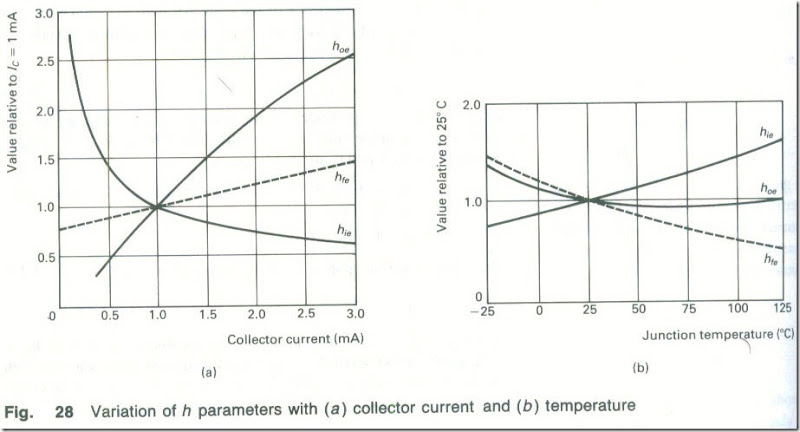
The h parameters of a bipolar transistor are not constant quantities but instead they vary with both the collector current and the temperature. Figs. 28(a) and (b) show typical variations of the three h parameters.

Mutual Conductance Circuit

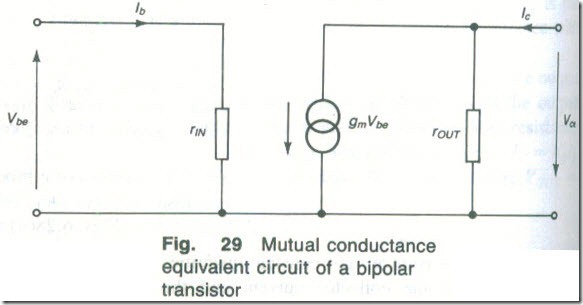
The ratio of h_ff to h_ie . which is the mutual conductance 8m. is how­ever, much more constant since h_fe and hif vary in different direc­lions . The value of 8m is primarily determined by the d.c. collector current (gm = 38 mS per mA of collector current) and it is easily predictable. Calculations of amplifier gain are therefore often based on the mutual conductance model of the transistor shown by Fig. 29. The output resistance r_out is often omitted since its effect on the voltage gain is generally small.

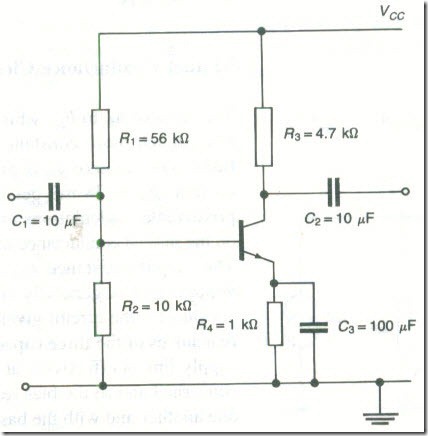
Consider the circuit given in Fig. 30. At signal frequencies the reactances of the three capacitors are negligibly small. The collector supply line is effectively at earth potential as far as a.c. signals are concerned and so the bias resistors R₁ and R₂ are in parallel both with one another and with the base-emitter terminals of the transistor. The

Fig. 28 Variation of h parameters with (a) collector current and (b) temperature

Fig. 29 Mutual conductance equivalent circuit of a bipolar transistor

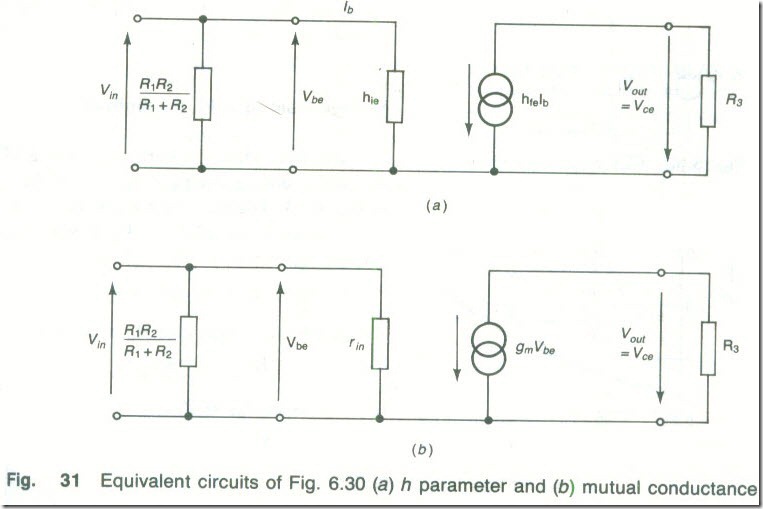
emitter resistor R₄ is effectively short circuited by capacitor C₃ and the collector resistor appears between the collector and the emitter. Thus, the h parameter and mutual conductance equivalent circuits of the amplifier are as given in Fig. 31(a) and (b).

The bias resistors shunt the signal path and so they reduce the input resistance of the circuit. To limit this shunting effect the bias resistors should have as high a resistance as possible.

 

If the parameters of the transistor are h_ie = 2000 Ω and h_fe = 120 and gm = 120/2000 = 60 mS , then the voltage gain of the circuit is

A_v = V_out/V_in = 120 x 4700/2000 = 282

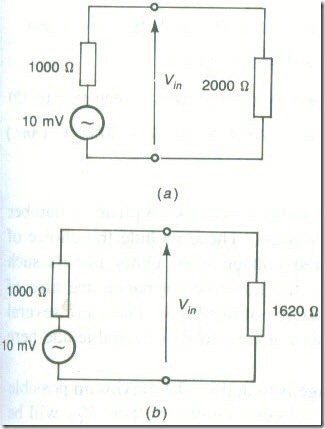
The presence of the bias resistors does not affect the voltage gain of the circuit but it does reduce the input voltage that appears across the input terminals Suppose that the source voltage has an e.m.f. of 10 mV and an internal resistance of 1000 Ω. Then, Fig. 32(a), the input voltage is V_in = 6.67 mV, V_out = 1.88 V, if the bias resistors are neglected. If, Fig. 32(b), the bias resistors are taken into account. the input resistance of the amplifier rill is found from 1/r_in = 1/2000 + 1/(56 x 10³) + 1/(10 X 10³) and r_in = 1620 Ω. Now the input voltage is 18 mV and V_out = 1.74 V.

The difference between the two output voltages obtained may seem to be fairly significant but it must be remembered that the quoted resistor values are all nominal values and are subject to tolerance

variations. Because of this, for practical purposes 8m is often taken as being equal to le/25 mS, or 40 mS per mA of collector current.

Voltage Gain of a FET Amplifier

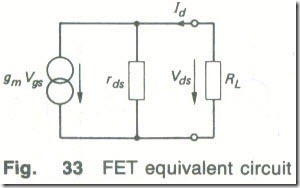
At audio-frequencies the performance of a FET can be described by its mutual conductance g_m = I_d/V_gs and the equivalent circuit shown in Fig. 33. The resistance r_ds is the output resistance of the FET and is equal to δV_DS/δI_D = V_ds/I_d with V_GS constant. The output voltage V_ds of the circuit is given by

V_ds = (g_mV_gsR_Lr_ds/(R_L + r_ds)

Therefore the voltage gain Ay is given by

A_v = V_ds/V_gs = g_mR_Lr_ds/(r_ds + R_L) (6.14)

If, as is usual, r_ds >> R_L

A_v = g_mR_L (6.15)

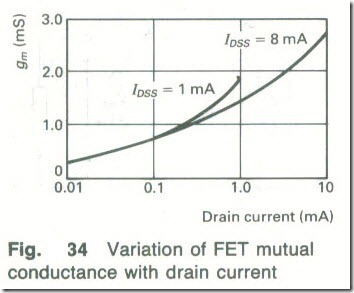
The mutual conductance of a FET is not a constant quantity but instead is a function of the drain current as shown in Fig 34. (loss is the drain current for V_GS = 0.)

Example 13

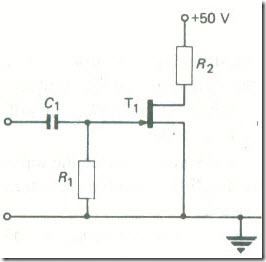
Calculate the drain load resistance required to give the circuit of Fig. 35 a voltage gain of 20. The FET used has g_m= 4 X 10^-3 S and r_ds = 100 kΩ .

Solution

From equation (6.14), A_v = 20 = (4 X 10^-3 X l0⁵R₂)/(l0⁵ + R₂)

Therefore R₂ = (20 x 10⁵)/380 = 5.26 kΩ (Ans.)

Alternatively, using the approximate expression given by equation (6.15) A_v = 20 = 4 X l0^-3R₂ or R₂ = 20/(4 x 10^-3) = 5000 Ω (Ans.)