Determination of Gain using a Load Line

Determination of Gain using a Load Line

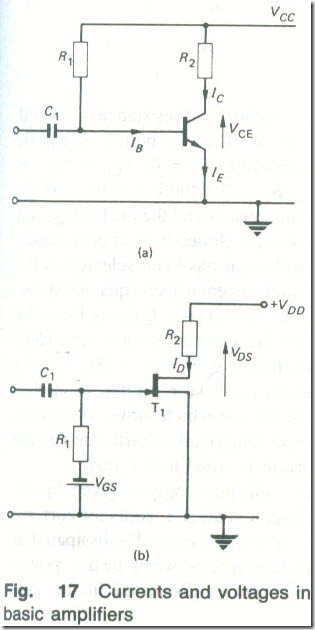
The voltage gain of a FET amplifier or the current gain of a bipolar transistor amplifier can be determined with the aid of a load line drawn on the output current-output voltage characteristics of the device. The currents and voltages existing in the collector or drain circuit of a simple resistance-loaded amplifier are shown in Figs. 17(a ) and (b) respectively. In each of these circuits the d.c. collector or drain current flows in the load resistor R₂ and develops a voltage across it. The direct voltage which is applied across the transistor or FET is equal to the supply voltage minus the d.c. load voltage.

 

Thus, referring to Fig 17

V_CE = V_CC – l_CR₂                      (6.7)

V_DS = V_DD – I_DR₂                    (6.8)

Equations (6.6) and (6.7) are of the form y = mx + c and are therefore equations of a straight line. In order to draw a straight line it is only necessary to plot two points; these points can best be determined in the following manner. Point A: Let I_C = I_D = 0 in equations (6.7) and (6.8) respectively, then

V_CE = V_CC and V_DS = V_DD

Point B: Let V_CE = V_DS = 0 equations (6.7) and (6.8) respectively, then

0 = V_CC – I_CR₂ or I_C = V_CC/R₂

0 = V_DD – I_DR₂ or I_D = V_DD/R₂

If the points A and B are marked on the characteristics and then joined together by a straight line, the line drawn is the load line for the particular values of load resistance and supply voltage. The load line can be used to determine the values of current and voltage in the output circuit, since the ordinate of the point of intersection of the load line and a given input current or voltage curve gives the output current or voltage for that input signal.

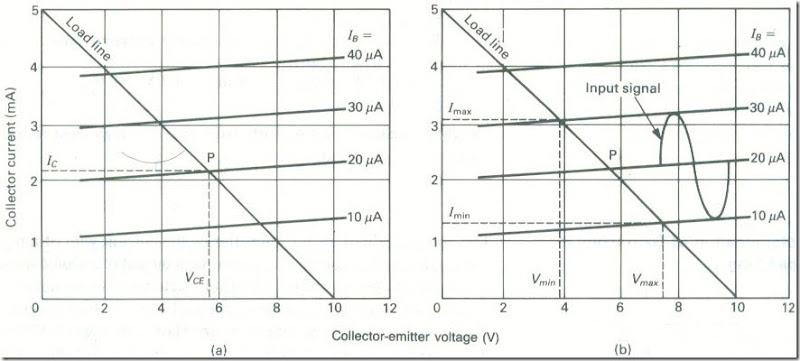
Consider for example, the output characteristics of an n-p-n transistor given in Figs.18(a) and (b), and suppose the transistor is to be used in an amplifier with a collector load resistance of 2000 Ω and a collector supply voltage of 10 V. The two points, A and B, that locate the ends of the load line are at I_C = 0, V_CE = V_CC = 10 V, and at V_CE = 0 , I_C = V_CC/R₂ = 10/2000 = 5 mA. These points have been located on the characteristics and the load line drawn between them. The operating point is often chosen to lie approximately in the middle of the load line, and here it has been selected as the point marked P. The required base bias current is then equal to 20 p.A. The d.c. collector-emitter voltage (V_CE = V_CC – l_CR₂) is found by projecting vertically downwards from the operating point to the voltage axis. This step is shown by a dashed line in Fig. 18(a) and it determines the standing (or quiescent) collector-emitter voltage as 5.6 V. Similarly, the d.c. collector current which flows is found by projecting horizontally from the operating point towards the current axis. Thus, the d.c. collector current is equal to 2.2 mA.

The d.c. power taken from the collector supply is given by the product of the collector supply voltage and the d.c. collector current, i.e. 10 X 2.2 X 10^-3 = 22 mW. The d.c. power Pc dissipated at the collector of the transistor is the difference between the d.c. power supplied to the circuit and the d.c. power dissipated in the load resistance. Hence

P_C = 22 X 10^-3 – [(2.2 X 10^-3)² X 2000] = 12.32 mW Pc is also equal to the product of the d.c. collector current and the quiescent collector-emitter voltage; thus

P_C = 2.2 X 10^-3 X 5.6 = 12.32 mW

The load line can also be used to find the variations in both the collector current and the collector-emitter voltage which are produced by the application of a signal to the base of the transistor. Suppose

as shown by Fig. 6. 18(b ) that a sinusoidal signal of peak value 10 p.A is applied to the transistor. This signal is superimposed on the base bias current of 20 p.A and so the base current is varied from a minimum value of 10 p.A to a maximum value of 30 p.A. The corres­ponding values of the collector current and the collector-emitter voltage are determined by projecting to the current and voltage axes from the points of intersection of the load line and the curves for IB = 10 p.A and IB = 30 p.A. This has been shown by the dashed lines drawn on Fig 18(b). The collector current is varied from a minimum value I_C(min) = 1.3 mA to a maximum value l_C(max) = 3.25 mA. The collector-emitter voltage is varied from a minimum value _VCE(min) = 3.6 V to a maximum value V_CE(max) = 7.3 V. The a.c. component of the collector current has a peak-to-peak value of (3.25 – 1.3) mA or 1.95 mA, while the peak-to-peak value of the a.c. component of the collector-emitter voltage is (7.3 – 3.6) or 3.7 V .

The current gain Ai of the amplifier is

Hence

A_i = (1.95 x 10^-3)/(20 x 10^-6) = 97.5

Example 7

The transistor used in a single-stage audio-frequency amplifier with a resistance load of 2000 Ω has the data given in Table 2.

Plot the output characteristics of the transistor and draw the load line assuming a collector supply voltage V_CC of 8 V.

(i) Select a suitable operating point.

(ii) Determine the current gain A_i when an input signal producing a base current swing of 5 μA about the chosen bias current is applied to the circuit.

(iii) Assuming the input resistance of the transistor is 1900 (1 determine the voltage gain A_v.

(iv) Calculate the power gain A_p .

Table 2

			lc(mA)
VCE(V)	IB = 5μA		–	IB =10μA		IB = 15 μA		IB = 20 μA
2	0.85		1.55		2.32		3.08
4	1.00		1.74		2.56		3.35
6	1.13		1.92		2.76		3.60
8	1.30		2.13		3.00		3.85

Solution

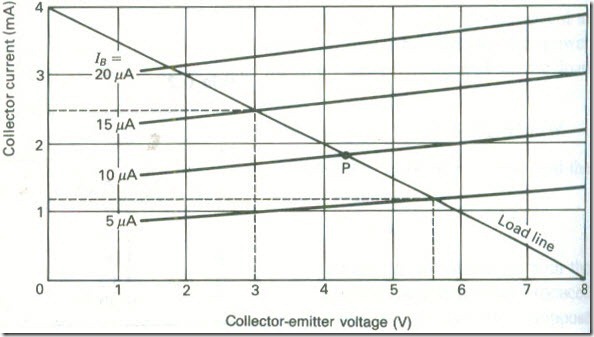
The output characteristics are shown plotted in Fig. 19. The d.c. load line must be drawn between the points

IC = 0, VCE = VCC = 8 V, and

V_CE = 0, I_C = V_CC/R₂ = 8/2000 = 4 mA

(i) Since the input signal has a peak value of ± 5 p.A a suitable base bias current is 10 p.A, the operating point is then P.

(ii) When a signal of ± 5 p.A peak is applied to the transistor, the base current varies between 5 p.A and 15 p.A. Projection from the intersection of the load line and the 5 p.A and 15 p.A base current curves to the current axes gives the resulting values of collector current as 1.15 rnA and 2.45 rnA.

The peak-peak collector current swing is therefore 2.45 – 1.15 or 1.30 mA and the current gain is

A_i = (1.3 x 10^-3)/(10 x 10^-6) = 130 (Ans.)

(iii) If the input resistance of the transistor is 1900 n the a.c. voltage applied to the transistor must be

± 5 x 10-⁶ x 1900 or ± 9.5 x 10^-3 V

Projecting from the intersection of the load line and the appropriate base current curves to the voltage axis gives the peak-peak collector Voltage as

5.7 – 3.08 = 2.62 V

Voltage gain Av = 2.62/(19 x 10^-3) = 138 (Ans.)

Alternatively, using equation (3.7)

Av = A_iR_L/R_in = (130 x 2000)/1900 = 137 (Ans.)

(iv) The power output of the transistor is the product of the r.m.s. values of the a.c. components of the collector current and the collector-emitter voltage. Therefore

Output power = (peak-peak I_c)/2√2 x (peak-peak V_ce)I2√2

= [(I_C(max) – _IC(min))]/8

= (1.3 X to^-3 X 2.62)/8 = 4.258 x 10^-4 W (Ans.)

The input power delivered to the transistor is

I²_b(rms)h_ie = [(5 X 10^-6)/√2]² X 1900 = 23.75 X 10^-9 W

Power gain A_p = P_out/P_in = 4.258 X 10^-4/23.75 X 10^-9 = 17928 (Ans.)

Alternatively, using equation (3.8),

A_p = A²_iR_L/R_in = A_iA_v = 130 x 137 = 17810 (Ans.)

 

Example 8

Determine the mutual conductance of the transistor in Example 4. Use this value to calculate the voltage gain of the circuit.

Solution

g_m = h_fe/h_ie = 130/1900 = 68.4 mS (Ans.)

or, g_m = 38 X 10^-3 X I_C = 38 X 10^-3 X 1.8 = 68.4 mS (Ans.)

Voltage gain = g_mR_L = 68.4 X 10^-3 X 2 X 10³ = l37 (Ans.)

Since the mutual conductance 8m is primarily determined by the d.c. collector current its value is more predictable than is the value of h_fe and so g_m is increasingly employed in performance calculations.

Example 9

The bipolar transistor used in an audio-frequency amplifier has h_ie = 250 and R_in = 1500 Ω . (a) Calculate the collector load resistance needed to give a voltage gain of 200. (b) A voltage source of e.m. f. 20 m V and internal resistance 600 n is connected to the input terminals of the amplifier. Calculate the output voltage.

Solution

(a) 200 = 250R_L/1500, R_L = (200 X 1500)/250 = 1200 Ω (Ans.)

(b) V_in = (20 X 15(0)(600 + 1500) = 14.29mV

V_out = 200 X 14.29 X 10^-3 = 2.86 V (Ans.)

A.C. Load Lines

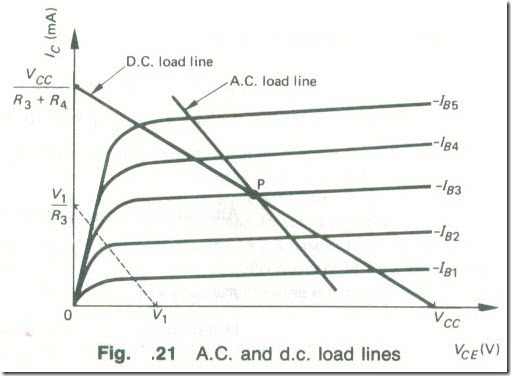
Very often the load into which a transistor or a FET works is not the same for both a.c. and d.c. conditions. When this is the case two load lines must be drawn on the characteristics: a d.c. load line to determine the operating point, and an a.c. load line to determine the current or voltage gain of the circuit. The a.c. load line must pass through the operating point.

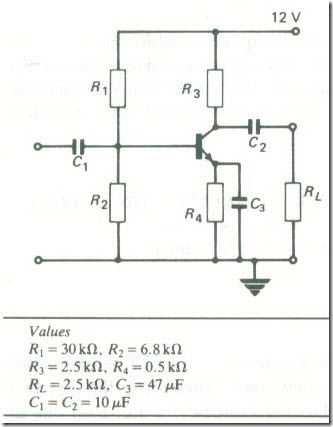
Fig.20 shows the circuit of a single-stage common-emitter amplifier using potential-divider bias. The emitter decoupling capacitor C₃ has a very high reactance at very low frequencies and does not shunt the emitter resistance R4 at zero frequency (direct current). The  d.c. load on the transistor is therefore R₃ + R₄ ohms. At signal frequencies the reactance of C₃ is low and the a.c. load on the transistor is reduced to R3 ohms. A d.c. load line is first drawn on the output characteristics between the points

Ic = 0, V_CE = V_CC, and

V_CE = 0, I_c= V_CC/(R₃ + R₄)

as shown by Fig. 21. A suitable operating point P is then selected .

 

The a.c. load line must be drawn passing through the operating pour with a slope equal 10 the reciprocal of the a.c. load resistance on the transistor, i.e. a slope of – 1/R₃. To avoid extending the current axis, proceed as follows. (a) Assume that the a.c. load is actually a d.c. load, and using any convenient value of supply voltage (V₁ in Fig 21), draw lightly me corresponding d.c. load line using the method previously explained, i.e. draw the line between the points V₁ and V₁/R₃· (b) This load line has the required slope, so now draw the actual a.c. load line parallel to it and passing through the operating point.

Another instance where the a.c. load on a transistor is different from the d.c. load is shown by Fig. 22. The external load resistance R_L, which may be me input resistance of a following amplifier stage, is coupled to the transistor by the coupling capacitor C₂. If the decoupling capacitor C₃ has negligible reactance at all signal frequencies the d.c. load on the transistor is R₃ + R₄ ohms and the a.c. load is R3 in parallel with R_L, i.e.

R_L(eff) = R₃R_L/(R₃ + R_L

Example 10

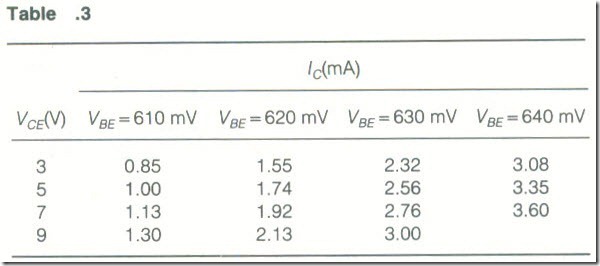
The bipolar transistor used in the circuit of Fig. 22 has the data given in Table 3. Plot the output characteristics of the transistor, draw the d.c.load line and select a suitable operating point. Draw the a.c. load line and use it to find the a.c. voltage across the 2500 Ω load R_L when an input signal V_be of peak value 15 mV is applied to the circuit. Assume all the capacitors have zero reactance at signal frequencies.

Solution

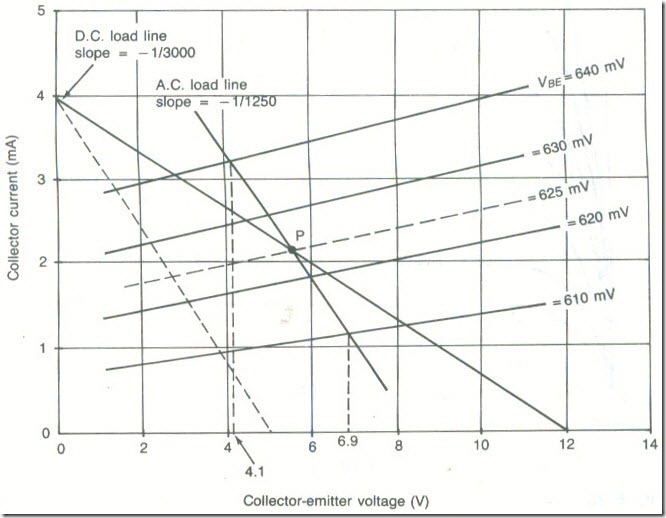
The output characteristics are shown plotted in Fig. 23. The d.c. load on the transistor is R₃ + R₄ 3000 Ω: the d.c. load line must therefore be drawn between the points

I_c= 0, V_CE = 12 V and

V_CE = 0, I_c = 12/3000 = 4 mA

Since the input signal has a peak value of 15 mV, a suitable base bias voltage is 625 mV, the operating point is then P.

The a.c. load on the transistor is the 2500 Ω collector resistor in parallel with the 2500 0 load, i.e. 1250 O. An a.c. load line with a slope of -1/1250

must therefore be drawn on the output characteristics. To draw a d.c. load line with the same slope assume a convenient supply voltage. say S Y: then this d.c. load line joins the points

V_CE= 5 V and l_c = 5/1250 = 4mA

The equivalent e.c. load line is shown dotted and the wanted a.c. load line has been drawn parallel to it and passing through the operating point.

When a signal of ± 15 mV (peak) is applied 10 the transistor V_BE varies between 610 mV and 640 mV. Projection from the intersection of the load line and the 610 mV and 640 mV V_BE: curves gives the resulting values of collector voltage as 4.1 V and 6.9 V. The peak collector signal voltage is therefore (6.9 – 4.1)/2 or 1.4 V.

Voltage Gain of FET Amplifier

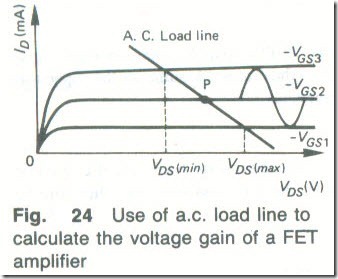
Fig. 24 calculate the voltage gain of a FET amplifier

The voltage gain of a FET amplifier can also be found with the aid of a load line. For example, Fig. 24 shows an a.c. load line drawn on the drain characteristics of a FET. and the dotted projections from the load line show how the drain voltage swing, resulting from the application of an input signal voltage. can be found. The voltage gain Av of the FET amplifier is

Example 11

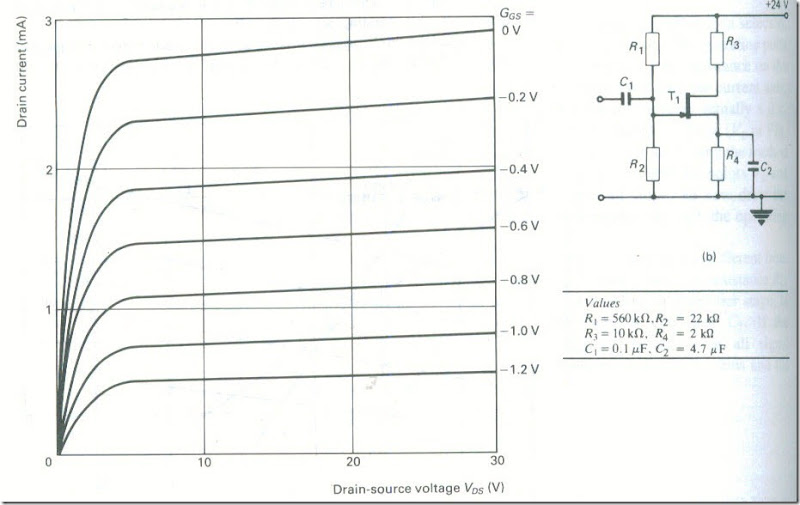
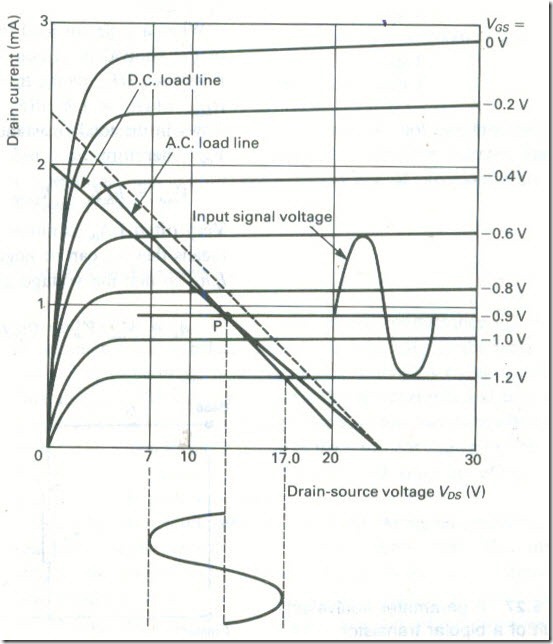
Fig. 25(a) shows the drain characteristics of a common-source n-channel lFET, which is used in the single-stage amplifier circuit shown in Fig. 25(b). Draw the d.c. load line and select a suitable operating point. Draw the a.c. load line and use it to find the voltage gain when a sinusoidal input signal or 0.3 v peak is applied.

Solution

The d.c. load on the FET is 12 kΩ, and hence the d.c. load line must join the points

I_D = 0 V_DS = 24 V and

V_DS = 0, I_D = V_DD/(R₃ + R₄) = 24/(12 x 10³) = 2 mA

The load line has been drawn in Fig. 26. A suitable operating point is V_GS = -0.9 V. The a.c. load line must pass through the chosen operating point

with a slope of -1/(10 x l0³ ) and it has been drawn parallel to the dotted line joining the points

I_D =0, V_DS = 24 V and V_DS =0, I_D = 24/(10 X 10³) = 2.4mA.

From the a.c. load line, the voltage gain of the circuit is

A_v = (17 – 7)/( -1.2 – (-0.6» = -16.7 (Ans.)