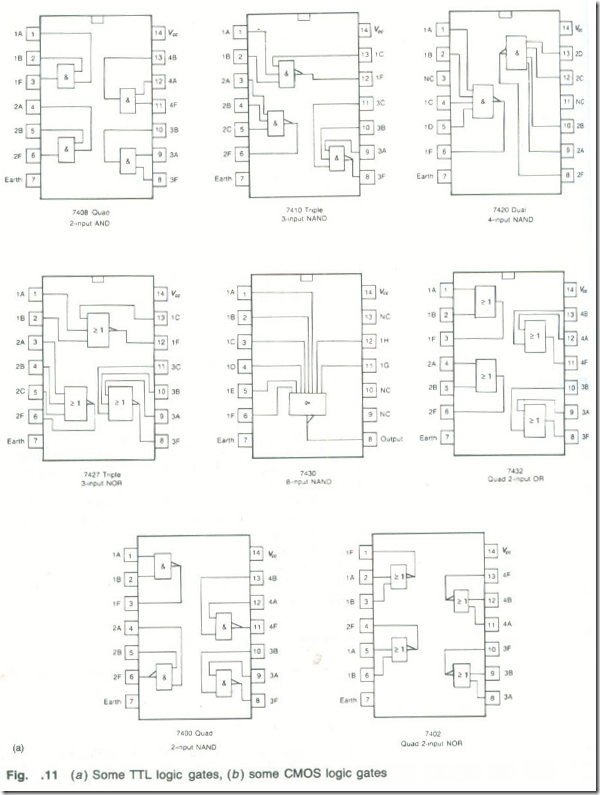
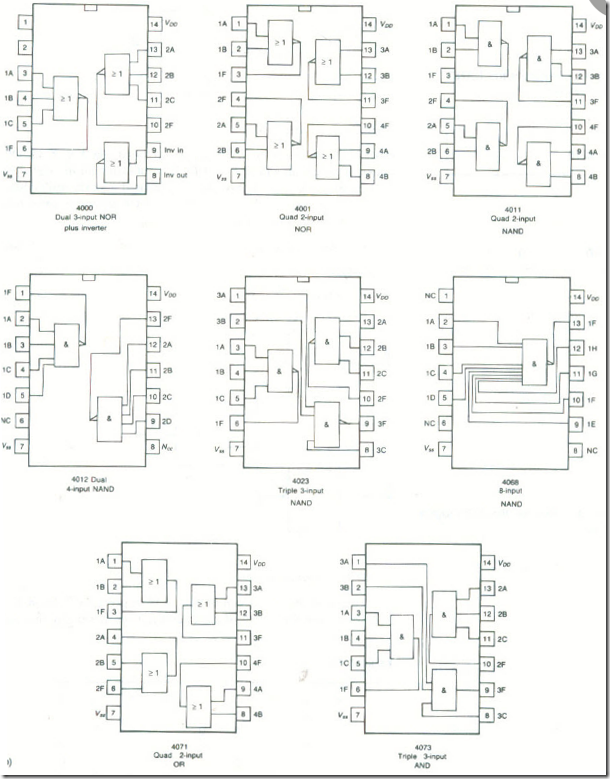
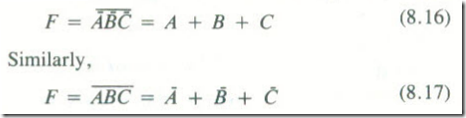Combinations of Gates
Very often it is convenient to be able to perform a logical function using a different kind of gate.
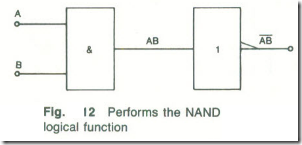
AND Followed by NOT
If an AND gate is followed by a NOT gate (see Fig.12) the output of the circuit will be 
. Therefore, the combination acts like a NAND gate.
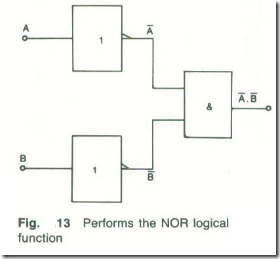
AND Preceded by NOT
If all of the inputs to an AND gate are inverted, see Fig .13, the output of the circuit will be F = Ā.Ḃ. The truth table for this equation is given by Table 8.10. If this table is compared with the truth tables of the various gates it will be seen that the NOR logical function has been performed.
Therefore,
Similarly
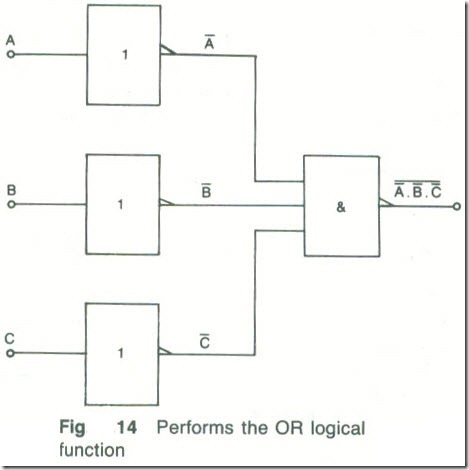
NAND Preceded by NOT
The truth table for the circuit of Fig. 14 is given by Table 11. This shows that the output of the circuit is 1 whenever any one, or
more, of its inputs is at 1. This means that the circuit performs the OR logical function. The Boolean expression for the circuit is
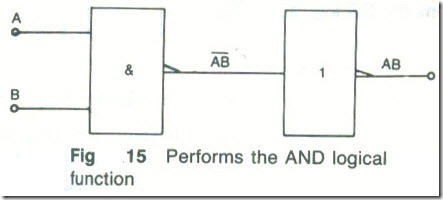
NAND Followed by NOT
When a NAND gate is followed by a NOT gate, Fig. 15, the AND function is performed.
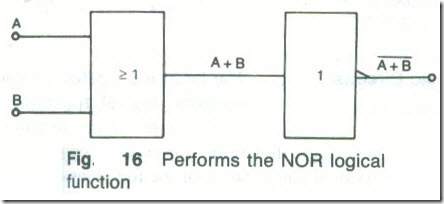
OR Followed by NOT
Fig .16 shows a 2-input OR gate that is followed by a NOT gate. The combination acts like a NOR gate.
OR Preceded by NOT
Fig .17 shows a 2-input OR gate that has both of its inputs fed via NOT gales. Table 12 gives the truth table of the circuit and shows that the circuit performs the logical function NAND. The Boolean expression describing the circuit is given by equation (8.18), i.e.
NOR Followed by NOT
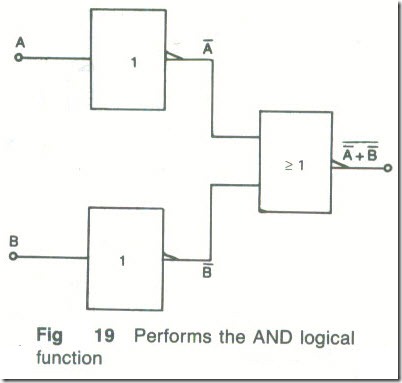
NOR Preceded by NOT
Fig. 19 shows a NOR gate both of whose inputs are passed through a NOT gate. The truth table of the arrangement is given by Table 13. The output of the circuit is at logical 1 only when both of its inputs are at logical 1. Hence, the circuit performs the AND logical function. The Boolean expression for the circuit is given by equation (8.19). i.e.
Combinational Logic Circuits
The basic logic gates are used in combination to form other, more complex, logical functions. These logic functions are formed by suitably inter-connecting the individual gates
. Some of the functions that may be required can also be obtained ‘ready-made’, as it were, in an SSI package. Logic functions can also be generated using LSI circuits known as ROMs and PLDs but only the use of the basic will be considered here.